帶無界非線性項的兩點邊值振蕩問題

何勇，徐博

帶無界非線性項的兩點邊值振蕩問題

何勇，徐博

(重慶科技學院數理學院，重慶401331)

假定非線性項為次線性的，利用Ekland變分原理證明非線性常微分分方程u″(t)+u(t)+f(t，u(t))=0存在無窮多解.

Ekeland變分原理;次線性;振蕩;第一特征值;局部極小;極大極小法

1 主要結論

考慮兩點邊值問題

其中f:［0，π］×R→R為連續可測泛函.

令f(t，x)是有界的，即存在h∈L1(0，π;R+)，使得對于任意的x∈R和t∈［0，π］有

［1－3］中，方程(1)在條件

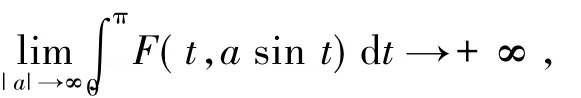
或條件

得出在有界條件(2)下，方程(1)具有無窮多個解.在文獻［5］中，方程的非線性項滿足如下2式

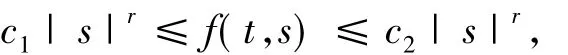
其中

其中

t∈［0，π］，s∈R，|s|≤δ，c3，c4，δ＞0，τ＞1

得出了合適條件下的多重性結論.在本文中，假設非線性項是次線性的，即存在g，h∈L1(0，π;R+)，α∈［0，1］使得

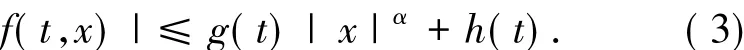
本文的主要結論為如下定理.

定理1在H10上定義泛函φ如下

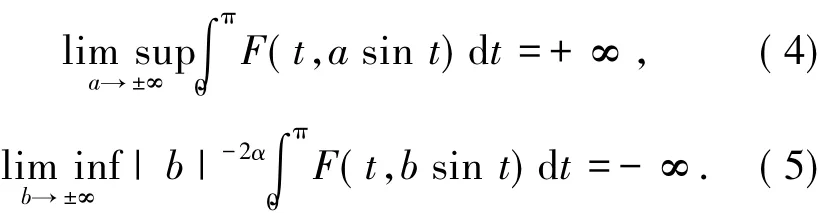
于是對方程(1)有如下結論:

1)存在一個解序列(un)，所有解都是泛函φ的極小極大型臨界點，且當n→∞時，φ(un)→+∞;

2)存在另一個解序列(u*n)，所有解都是泛函φ的局部極小，且當n→∞時，φ(u*n)→－∞.

推論1假設f(t，x)滿足(3)式.進一步假設

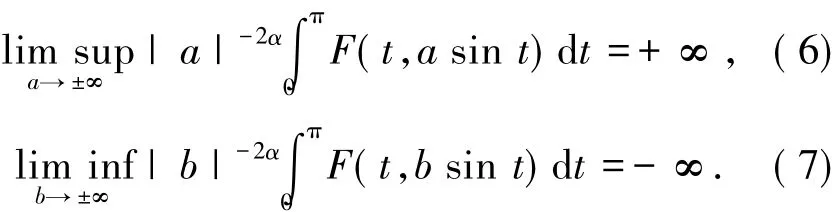
于是對方程(1)有如下結論:

1)存在一個解序列(un)，所有解都是泛函φ的極小極大型臨界點，且當n→∞時，φ(un)→+∞;

注1文獻［4］中的定理1是本文定理1在α =0時的一個特例.此外本文的結論區別于之前的其他結論.

2 定理證明

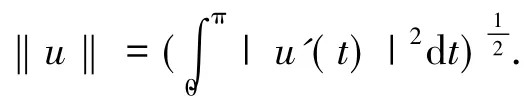
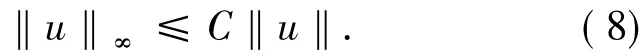
眾所周知問題(1)的弱解是泛函φ的臨界點.

證明由條件(3)可得(8)和(9)式，故有

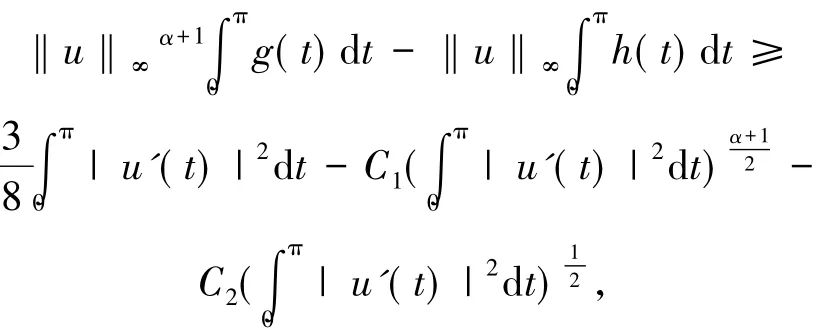
C1、C2為正常數且u∈.從以上不等式知命題成立.

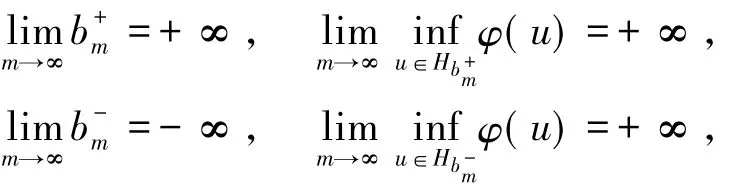
證明令u=珔u+珘u，其中珔u=b sin t，珘u∈珟H.對每一個ε＞0，由Cauchy不等式［7］和估計(8)式

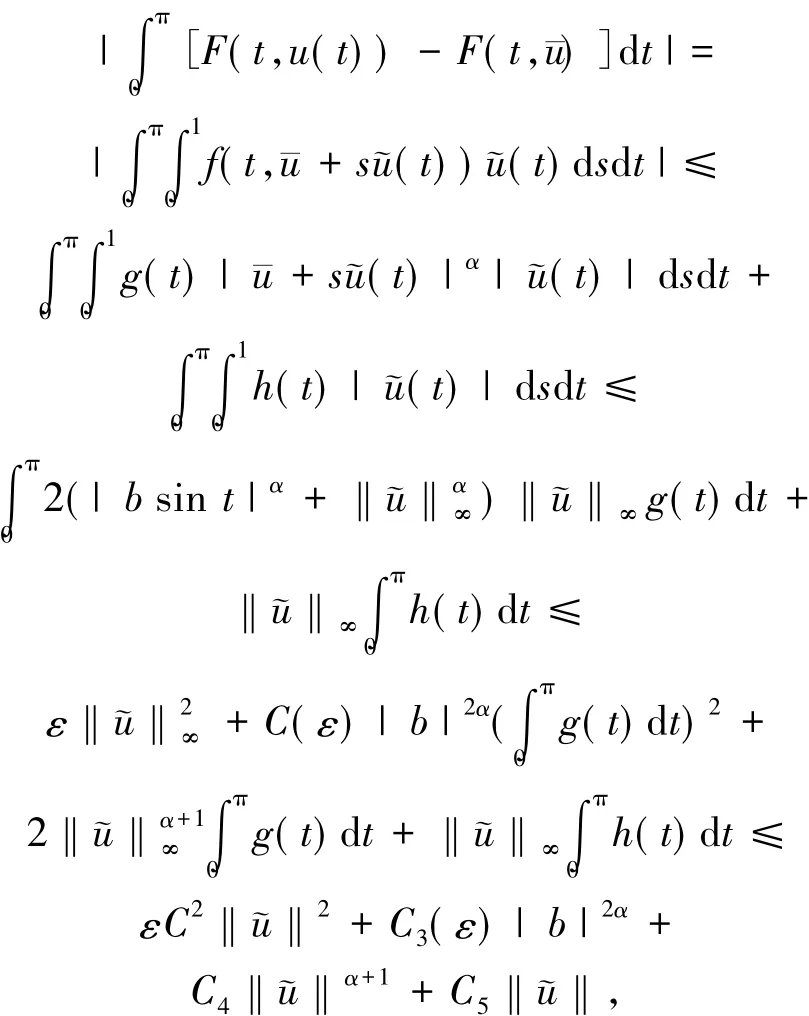
其中C(ε)、C3(ε)、C4、C5正常數.令ε=1/8C2有

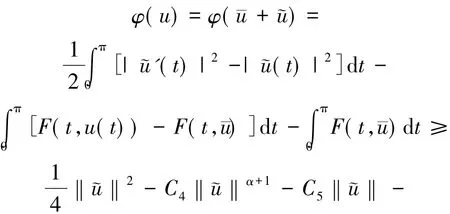
由條件(5)和上述不等式知命題成立.

定理1的證明令

因此由cn≥M及命題2有，對于所有較大的n，

對于如此的n，在Sn中存在序列(γk)使得當k→∞時有

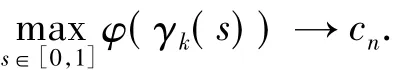
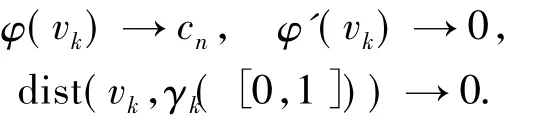
現在證明序列(vk)在上有界.對于充分大的k有

且存在wk∈γk(［0，1］)使得

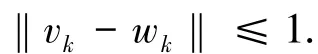
對于固定的n，由命題3，存在m，使得γk(［0，1］)與超平面{sin t}+珟H不相交.令wk=珔wk+珘wk，其中珔wk=dksin t且珘wk∈，于是

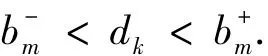
此外

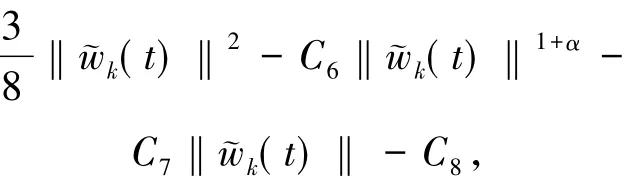
C6、C7、C8為正常數.于是(t)有界.因此，wk有界.同時vk在上有界.

現在vk是有界的，由文獻［2］中命題4.1的證明可知，vk中可得到一個收斂子列，仍記為vk.令un，則有

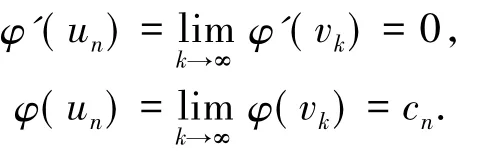
因此，un是一個臨界點且cn是泛函φ的臨界值.對于任意的γ∈Sn，如果＜＜，則γ相交于超平面={sin t}+.于是，

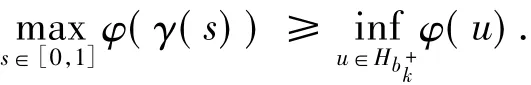
由此不等式和命題3可推出

所以定理1的第一個結論得證.

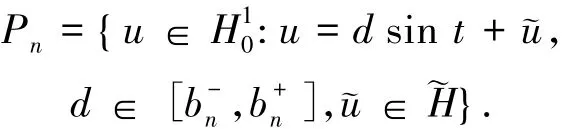
對于u∈Pn有

其中C9、C10、C11是正常數，則φ在Pn上下方有界.

定義

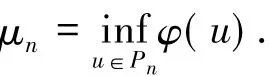
令(uk)是Pn上的極小化序列，即當k→∞時，φ(uk)→μn.從上述不等式知，(uk)在上有界.于是存在一個子序列，仍記為(uk)，使得uk?.由于Pn是的閉凸子集，∈Pn.且φ是弱下半連續的，故有

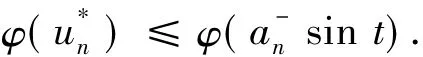
由命題2有

定理1證明完畢.

參考文獻

［1］AHMAD S，LAZER A C，PAUL J L.Elementary critical point theory and perturbations of elliptic boundary value problems at resonance［J］.Indiana Univ Math J，1976，25:933－944.

［2］MAWHIN J，WILLEM M.Critical point theory and Hamiltonian systems［C］//Appl Math Sci，74.New York:Springer－Verlag，1989.

［3］RABINOWITZ P H.Some minimax theorems and applications to nonlinear partial differential equations［C］//Cesari，Kannan，Weinbeiger.Nonlinear Analysis.New York:Academic Press，1978:161－177.

［4］HABETS P，MANASEVICH R，ZANOLIN F.A nonlinear boundary value problem with potential oscillating around the first eigenvalue［J］.J Diff Eqns，1995，117:428－445.

［5］SU J B，LI H.Multiplicity results for the two－point boundary value problems at resonance［J］.Acta Math Sci，2013，26:152－162.

［6］TANG C L.Periodic solutions for nonautonomous second systems with sublinear nonlinearity［J］.Proc Am Math Soc，1998，126: 3263－3270.

［7］EVANS L C.Partial Differential Equations［M］.Providence RI:Am Math Soc，1998.

［8］TANG C L.Solvability of Neumann problem for elliptic equations at resonance［J］.Nonlinear Anal，2001，44:323－335.

［9］TANG C L.Some existence theorems for the sublinear Neumann boundary value problem［J］.Nonlinear Anal，2012，48:1003－1011.

［10］TANG C L.Multiple solutions of Neumann problem for elliptic equations［J］.Nonlinear Anal，2013，54:637－650.

［11］TANG C L，WU X P.Existence and multiplicity for solutions of Neumann problem for semilinear elliptic equations［J］.J Math Anal Appl，2013，288:660－670.

［12］MITREANU D，PAPAGEORGIOU N S.Existence and multiplicity of solutions for Neumann problems［J］.J Diff Eqns，2007，232:1－35.

［13］頓調霞，李永祥.一類三階微分方程的兩點邊值問題的正解［J］.四川師范大學學報(自然科學版)，2014，37(6):810－813.

［14］劉瑞寬.一類奇異三階兩點邊值問題正解的存在性［J］.四川師范大學學報(自然科學版)，2014，37(4):482－486.

［15］趙亮，李樹勇，張秀英，等.一類含連續分布時滯的隨機Hopfiled神經網絡模型的幾乎必然指數穩定性和p階矩指數穩定性［J］.四川師范大學學報(自然科學版)，2013，36(3):1－5.

Two Point Boundary Value Oscillating Problem with Unbounded Nonlinearity

HE Yong，XU Bo
(Department of Mathematics and Physics，Chongqing University of Science and Techonology，Chongqing 401331)

In this paper，we employ the Ekeland’s variational principle to prove the existence of infinitely many solutions for the nonlinear ordinary differencial equation u″(t)+u(t)+f(t，u(t))=0，and so that the nonlinearity is sublinear.

Ekeland’s variational principle;sublinear;oscillating;first eigenvalue;local minimum;minimax methods

O175.8

A

1001－8395(2016)03－0369－04

10.3969/j.issn.1001－8395.2016.03.012

(編輯周俊)

2016－01－04

國家自然科學基金青年基金(61201065)

何勇(1982—)，男，講師，主要從事概率統計的研究，E－mail:heyongmath@163.com

2010 MSC:34B10;34B15