廣義松弛擬單調映射以及廣義松弛擬凸函數

蒲思思，何詣然

廣義松弛擬單調映射以及廣義松弛擬凸函數

蒲思思，何詣然*

(四川師范大學數學與軟件科學學院，四川成都610066)

介紹集值映射在賦范空間中的一種新的單調性，稱之為廣義松弛擬單調.運用KKM理論，證明變分不等式在新引入的單調映射下解的存在性.此外，還證明廣義松弛μ擬凸函數的次微分是廣義松弛μ擬單調的.

變分不等式;廣義松弛擬單調算子;廣義松弛擬凸函數;次微分

1 預備知識

本文所討論的變分不等式模型為:尋找x∈K使得

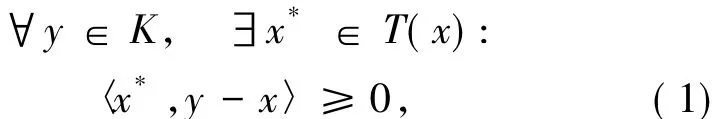
其中，K是賦范空間X中的非空凸子集，X*表示X的對偶空間，集值映射T:K→2X*{?}.為了方便，用VI(T，K)來表示問題(1).

近年來，學者們深入研究了變分不等式問題解的存在性.為了證明變分不等式有解，許多學者對映射T提出了各種廣義單調性假設，如偽單調性、擬單調性、真擬單調性、稠密偽單調性，可參考文獻［1－6］.文獻［7－9］證明了當T是稠密松弛μ偽單調單值映射時，變分不等式的解集非空.文獻［10］討論了變分不等式模型中的集合無界時，在映射具有偽單調或者擬單調性質時，加上某些強制性條件則可保證變分不等式的解集非空.在文獻［11］中，Y.P.Fang等提出松弛η－α單調，并且證明了在自反的Banach空間中，當映射T是松弛η－α單調時，似變分不等式問題解的存在性.文獻［12］提出松弛η－α偽單調映射，并且論證了在自反的Banach空間中，當映射T是松弛η－α偽單調時，似變分不等式問題的解集非空.在文獻［13］中，M.R.Bai等提出松弛μ擬單調集值映射，并且證明了在這種映射下變分不等式解的存在性.文獻［13］還提出一類松弛擬凸函數，并證明了這類函數的次微分是松弛擬單調的.當T是單值映射且具有松弛η－α擬單調性或松弛η－α真擬單調性時VI(T，K)解的存在性情況首次在文獻［14］中被提及.

受文獻［7－9，13－14］的啟發，在本文中提出了廣義松弛擬單調映射.對于這樣的映射，證明了VI (T，K)解的存在性，并將廣義松弛擬單調映射的相關結論延伸到了松弛φ擬單調映射.引入廣義松弛μ擬凸函數，并證明了這類函數與其對應次微分的廣義松弛μ擬單調性之間的等價關系.本文的結論推廣了文獻［7－9，13－14］中的相關結果.

2 具有廣義松弛擬單調映射的變分不等式問題

給定x，y∈X，線結［x，y］表示下面的集合

集值映射T:K→2X*{?}被稱為沿線結上半連續的，如果映射T限制在集合K的每一個線結上是關于X*的弱*拓撲上半連續的.用S(T，K)表示VI(T，K)的解集

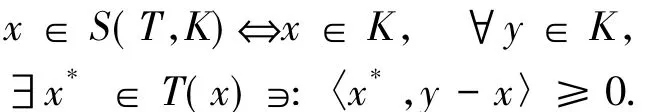
用LM(T，K)表示對偶變分不等式的局部解［5］其中N(x)是x的鄰域系.

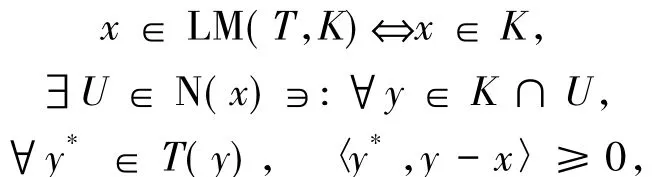
下面的定義1推廣了文獻［9，13］中的定義1.1.除非特別說明，本文總是假設μ＞0，α＞1.

定義1集值映射T:K→2X*{?}被稱為廣義松弛μ擬單調的，如果對任意x，y∈K和x*∈T(x)，y*∈T(y)有如下蘊含關系成立

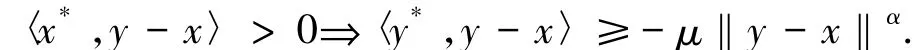
同樣地，給出廣義對偶變分不等式問題:尋找x∈K使得

其中，RM(T，K)表示x∈K且滿足(2)式的所有x的集合.

下面的定義2推廣了文獻［13］中的定義2.1.

定義2集值映射T:K→2X*{?}被稱為廣義真松弛μ擬單調的，如果對任意x1，x2，…，xn∈K和任意x∈co{x1，x2，…，xn}，存在i∈{1，2，…，n}使得?x*∈T(xi)，〈x*，xi－x〉≥－μ‖xi－x‖α.

命題1如果T:K→2X*{?}是廣義真松弛μ擬單調的，則它是廣義松弛μ擬單調的.

證明假設對任意x，y∈K，存在x*0∈T(x)使得〈x*0，y－x〉＞0.取xt=x+t(y－x)∈co{x，y}，t∈(0，1).因為T是廣義真松弛μ擬單調的，對任意的t∈(0，1)，可以得到

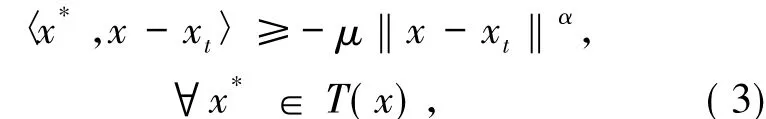
或者

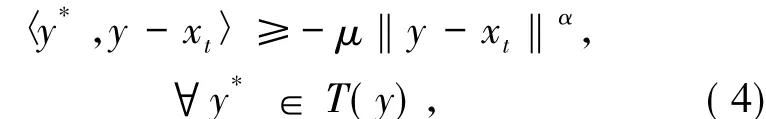
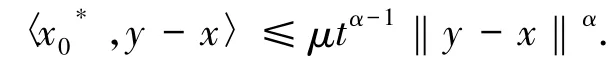
然而(3)式蘊含由于α＞1，當t∈(0，1)充分小時，該式顯然與〈x*0，y－x〉＞0矛盾.因此，對充分小的t∈(0，1)有(4)式成立.對(4)式取極限t→0+得

〈y*，y－x〉≥－μ‖y－x‖α，?y*∈T(y)，即T是松弛μ擬單調的.

為了幫助后面的證明，給出下面的定義和引理(參見文獻［13，15］).

定義3集值映射G:K→2X被稱為是KKM映射，如果對任意x1，x2，…，xn∈K有下式成立

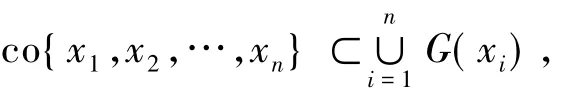
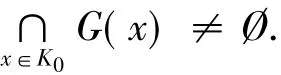
引理2設K是X的非空凸子集，如果T:K→2X*{?}是具有弱*緊值的沿線結上半連續的集值映象，則有

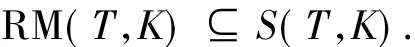
證明設x∈RM(T，K)，由RM(T，K)的定義有

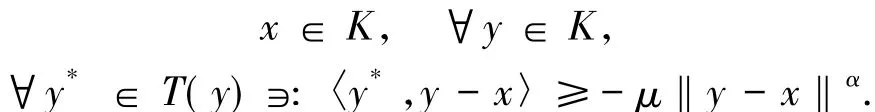
取zt:=x+t(y－x)∈K，其中t∈(0，1)，則對任意的其中，co{x1，x2，…，xn}表示{x1，x2，…，xn}的凸包.

引理1假設K是Hausdorff拓撲向量空間X的非空緊凸子集，K0是K的非空子集，G:K0→2K是一個KKM映射，如果對任意x∈K0，G(x)在X中是閉的，則有∈T(z)有t

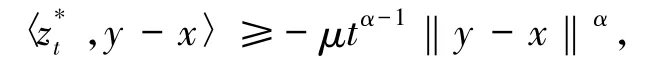
因此當t充分小時

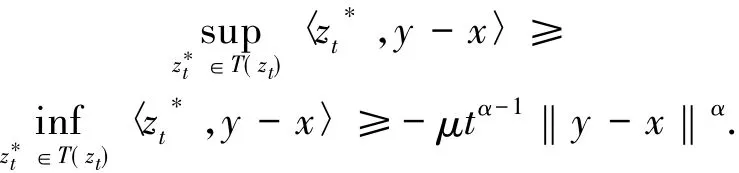
因為T是沿線結上半連續的，取極限t→0+，可以推出

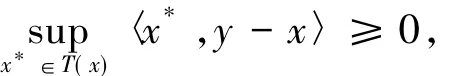
因為T具有弱*緊值，因此

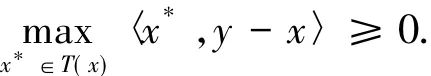
故對任意y∈K，存在x*∈T(x)有〈x*，y－x〉≥0.所以x∈S(T，K).故RM(T，K)?S(T，K).

對每一個廣義松弛μ擬單調映射，有如下命題成立.

命題2設K是賦范空間X中的非空凸子集，如果T:K→2X*{?}是廣義松弛μ擬單調映射，則在下面2個命題中至少有一個成立:

1)T是廣義真松弛μ擬單調映射;

2)LM(T，K)≠?.

證明假設T不是廣義真松弛μ擬單調映射，則存在x1，x2，…，xn∈K，x∈co{x1，x2，…，xn}，對任意i∈{1，2，…，n}，存在∈T(xi)使得

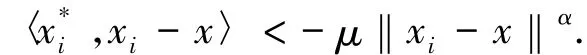
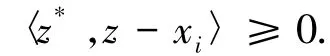
又因為x∈co{x1，x2，…，xn}，故

〈z*，z－x〉≥0，?z∈K∩U，?z*∈T(z)，這意味著x∈LM(T，K)，因此LM(T，K)≠?.

上面的命題2蘊含了本文中相關變分不等式解的存在性的主要結果.

定理1設K是賦范空間X中的非空緊凸子集，如果T:K→2X*{?}是具有弱*緊值的沿線結上半連續的廣義松弛μ擬單調映射，則S(T，K)≠?.

證明由命題2可得LM(T，K)≠?或者T是廣義真松弛μ擬單調映射.如果LM(T，K)≠?，因為T是具有弱*緊值的沿線結上半連續映射，故LM(T，K)?S(T，K)(參見文獻［5］)，因此S(T，K)≠?.另一方面，如果T是廣義真松弛μ擬單調映射，定義集值映射G:K→2K{?}且

G(x)={y∈K:〈x*，x－y〉≥－μ‖x－y‖α，?x*∈T(x)}.

根據T的廣義真松弛擬單調性，對任意x1，x2，…，xn∈K和任意y∈co{x1，x2，…，xn}，存在i∈{1，2，…，n}，對任意x*i∈T(xi)使得

因此

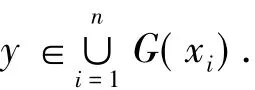
故G(x)是一個KKM映射.此外，對任意x∈K，G(x)是閉集;因此，如果K是緊集，對任意x∈K，G(x)是緊集.根據引理1可得

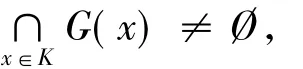
這等價于RM(T，K)≠?.最后，由引理2可得S(T，K)≠?.

接下來，給出定義在無界集上的VI(T，K)解的存在性.對于集值映射T:K→2X*{?}考慮如下強制性條件［13］

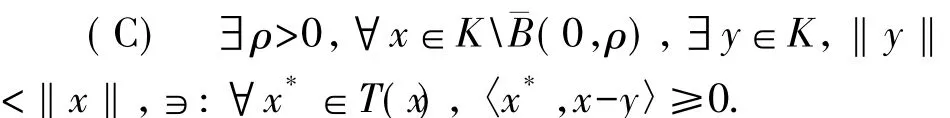
定理2設K是賦范空間X中的非空無界凸子集，如果T:K→2X*{?}是具有弱*緊值的沿線結上半連續的廣義松弛μ擬單調映射，且T滿足強制性條件(C)，假設存在ρ'＞ρ使得K∩珔B(0，ρ')是非空緊集，則S(T，K)≠?.

證明設K'ρ=K∩珔B(0，ρ').由定理1可得S(T，K'ρ)≠?.取x0∈S(T，K'ρ)，則‖x0‖≤ρ'.

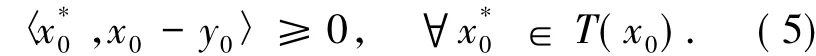
如果‖x0‖=ρ'，由強制性條件(C)，存在y0∈K∩B(0，ρ')使得對任意y∈K，取yt=(1－t)y+ty0，其中t∈(0，1)，使得yt∈K'ρ，其中K'ρ是凸集.因為x0∈S(T，K'ρ)，則存在∈T(x0)使得

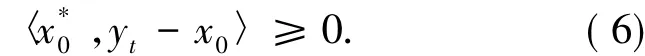
如果‖x0‖＜ρ'，取y0=x0，則可得x0∈S(T，K).

3 具有松弛φ擬單調映射的變分不等式問題

定義4［14］映射T:K→X*被稱為是η－α擬單調的，如果存在映射η:K×K→X和函數α:X→R并且對任意t＞0和z∈X有α(tz)=tpα(z)成立，使得對任意x，y∈K有如下蘊含關系成立

其中p＞1是常數.

在定義4的基礎上，給出如下松弛φ擬單調映射的定義，該定義推廣了本文中的定義1.

定義5集值映射T:K→2X*{?}被稱為是松弛φ擬單調的，如果對任意x，y∈K，存在x*∈T(x)，對任意y*∈T(y)，存在函數φ:X×X→R且對任意t＞0函數滿足φ(x+t(y－x)，x)=tpφ(y，x)，有如下蘊含關系成立

同樣地，給出對偶變分不等式問題:尋找x∈K使得

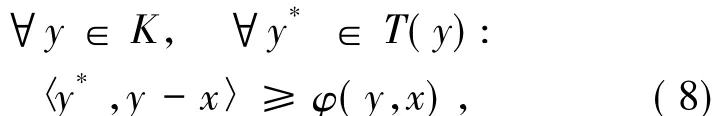
這里用RMφ(T，K)表示x∈K且滿足(8)式的所有x的集合.

特例11)如果φ(y，x)=0，則(7)式蘊含

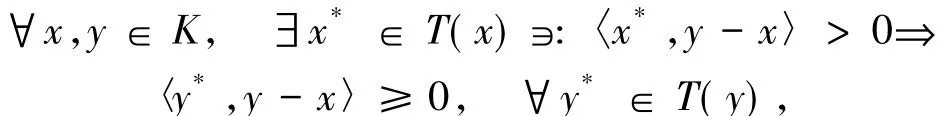
故T是擬單調映射;

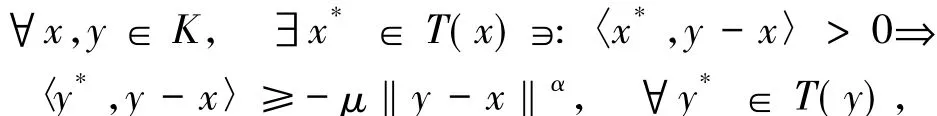
2)如果φ(y，x)=－μ‖y－x‖α，則(7)式蘊含故T是廣義松弛μ擬單調映射.顯然當α=p時φ(x+t(y－x)，x)=tPφ(y，x)成立.

下面，給出如下真松弛φ擬單調映射的定義，該定義推廣了本文中的定義2.

定義6集值映射T:K→2X*{?}被稱為是真松弛φ擬單調的，如果存在函數φ:X×X→R且對任意t＞0有φ(x+t(y－x)，x)=tpφ(y，x)成立，則對任意x1，x2，…，xn∈K和任意x∈co{x1，x2，…，xn}，存在i∈{1，2，…，n}，對任意∈T(xi)使得

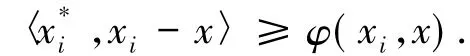
命題3如果T:K→2X*{?}是真松弛φ擬單調集值映射，假設函數φ:X×X→K關于第二變量是連續函數且φ滿足:

1)φ(y，x)=φ(x，y);

2)對任意t＞0，φ(x+t(y－x)，x)=tpφ(y，x)，則T是松弛φ擬單調映射.

證明假設對任意x，y∈K，存在x*0∈T(x)有〈x，y－x〉＞0.取xt=x+t(y－x)，t∈(0，1)，因為T是真松弛φ擬單調映射，對任意t∈(0，1)，可以得到

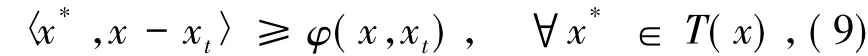
或者

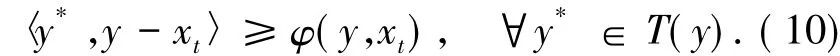
然而，由(9)式和φ滿足的條件可以推出

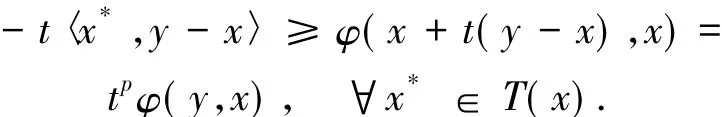
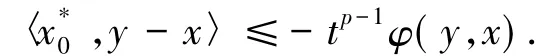
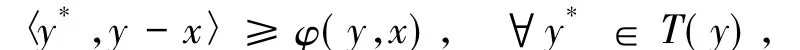
即T是松弛φ擬單調的.

引理3設K是賦范空間X中的非空凸子集.如果T:K→2X*{?}是具有弱*緊值的沿線結上半連續的集值映像，函數φ:X×X→K且對任意t＞0滿足

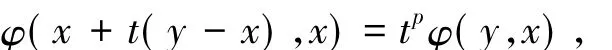
則RMφ(T，K)?S(T，K).

證明設x∈RMφ(T，K)，由RMφ(T，K)的定義有

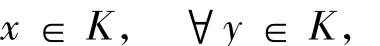
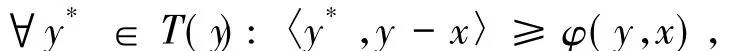
取zt:=x+t(y－x)，其中t∈(0，1)，則有

由(11)式可得

因此，當t充分小時

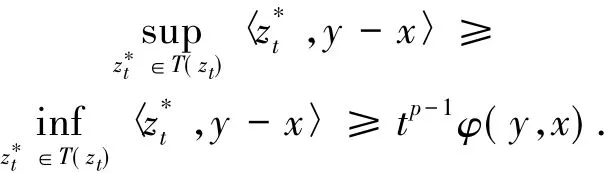
因為T是沿線結上半連續的，取極限t→0+，可以推出

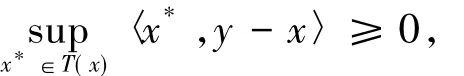
又因為T具有弱*緊值，因此

也就意味著對任意y∈K，存在x*∈T(x)有〈x*，yx〉≥0.所以x∈S(T，K).故RMφ(T，K)?S(T，K).

接下來證明了對每一個松弛φ擬單調映射，有如下命題成立.

命題4設K是賦范空間X中的非空凸子集，如果T:K→2X*{?}是松弛φ擬單調映射且函數φ:X×X→K關于第二變量連續并且對任意t＞0滿足

則在下面2個命題中至少有一個成立:

1)T是真松弛φ擬單調映射;

2)LM(T，K)≠?.

證明假設T不是真松弛φ擬單調映射，則存在x1，x2，…，xn∈K和x∈co{x1，x2，…，xn}，對任意i∈{1，2，…，n}，存在∈T(xi)使得

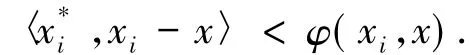
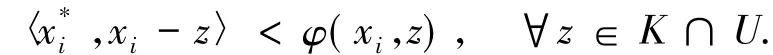
因為T是松弛φ擬單調映射，則對任意i∈{1，2，

…，n}和任意z*∈T(z)有下式成立

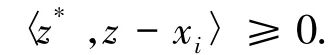
又因為x∈co{x1，x2，…，xn}，故有

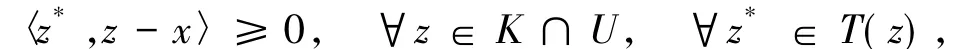
這意味著x∈LM(T，K)，因此LM(T，K)≠?.

定理3設K是賦范空間X中的非空緊凸集，如果T:K→2X*{?}是具有弱*緊值的沿線結上半連續的松弛φ擬單調映射，函數φ:X×X→K滿足:

1)φ是非對稱的，則φ(y，x)=φ(x，y)，?x，y∈X;

2)φ滿足φ(x+t(y－x)，x)=tpφ(y，x)，?x，y∈X，t＞0;

3)φ關于第二變量連續，

則S(T，K)≠?.

證明由命題4可得LM(T，K)≠?或者T是真松弛φ擬單調映射.如果LM(T，K)≠?，因為T是具有弱*緊值的沿線結上半連續的松弛φ擬單調映射，故LM(T，K)?S(T，K)(參見文獻［5］)，因此S(T，K)≠?.另一方面，如果T是真松弛φ擬單調映射，定義集值映射G:K→2K{?}滿足

G(x)={y∈K:〈x*，x－y〉≥

φ(y，x)，?x*∈T(x)}.

根據T的松弛φ擬單調性可知，對任意x1，x2，…，xn∈K和任意y∈co{x1，x2，…，xn}，存在i∈{1，2，…，n}，對任意∈T(xi)使得

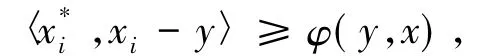
因此故G(x)是KKM映射.此外對任意x∈K，G(x)是閉集;因此，如果K是緊集，對任意x∈K，G(x)也是緊集.由引理1得這意味著RMφ(T，K)≠?.最后，由引理3易得S(T，K)≠?.

同樣給出了定義在無界集上的具有松弛φ擬單調映射的VI(T，K)解的存在性.

定理4設K是賦范空間X中的非空無界凸子集，如果T:K→2X*{?}是具有弱*緊值的沿線結上半連續的松弛φ擬單調映射且滿足強制性條件(C)，假設存在ρ'＞ρ使得K∩珔B(0，ρ')是非空緊集，函數φ:X×X→K滿足:

1)φ是非對稱的，則φ(y，x)=φ(x，y)，?x，y∈X;

2)φ滿足φ(x+t(y－x)，x)=tpφ(y，x)，?x，y∈X，?t＞0;

3)φ關于第二變量連續，

則S(T，K)≠?.

證明設K'ρ=K∩珔B(0，ρ').由定理3可得S(T，K'ρ)≠?.取x0∈S(T，K'ρ)，則‖x0‖≤ρ'.如果‖x0‖=ρ'，由強制性條件(C)得，存在y0∈K∩B(0，ρ')使得

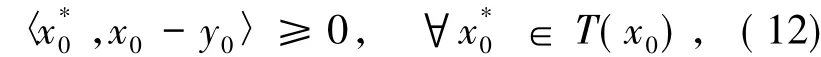
對任意y∈K，取yt=(1－t)y+ty0，其中t∈(0，1)，使得yt∈K'ρ，其中K'ρ是凸集.因為x0∈S(T，K'ρ)，則存在∈T(x0)使得

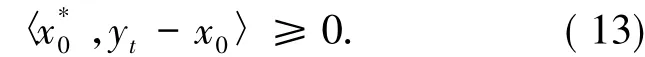
如果‖x0‖＜ρ'，取y0=x0，則可得x0∈S(T，K).

4 廣義松弛μ擬凸函數

在非光滑松弛擬凸函數的基礎上，給出了非光滑廣義松弛μ擬凸函數的相關內容.除非特別說明，在這部分內容中總是假設X是具有?－光滑再賦范［16］的Banach空間，函數f:X→R∪{+∞}是下半連續的，?f表示函數f的任意次微分(參見文獻［16］).

定義7下半連續函數f:X→R∪{+∞}被稱為是廣義松弛μ擬單調的，如果對任意x，y∈X有如下蘊含關系成立

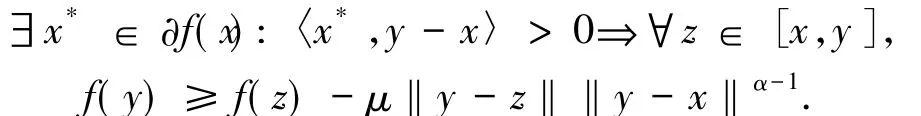
引理4［16］設a，b∈X且a∈dom f，a≠b，設r∈R使得r≤f(b)，則存在c∈［a，b］，c≠b以及序列xn→c，x*n∈?f(xn)使得

并且

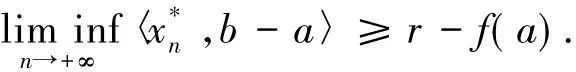
命題5設X是具有?－光滑再賦范的Banach空間，函數f:X→R∪{+∞}是下半連續的，如果?f是廣義松弛μ擬單調映射，則f是廣義松弛μ擬凸函數.

證明假設?f是廣義松弛μ擬單調映射，設x∈dom?f，y∈dom f，x≠y以及z∈［x，y］，z≠y使得

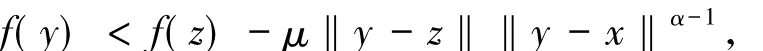
則可以找到μ0＞μ使得

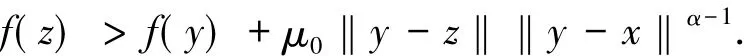
取

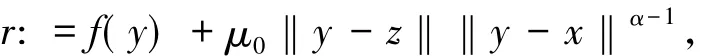
并對y，z運用引理4可知存在c∈［y，z］且c≠z以及序列xn→c和∈?f(xn)滿足

并且

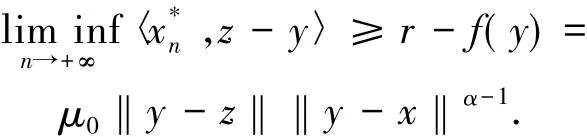
取u=c+t(z－y)，其中t＞0.因此

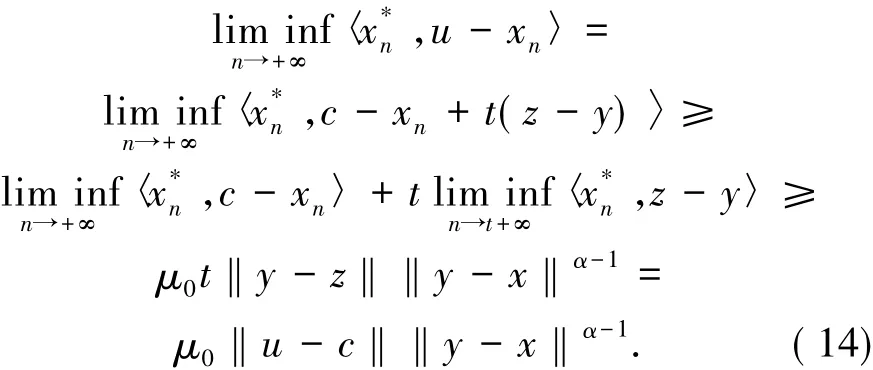
特別地，取u=x，由于

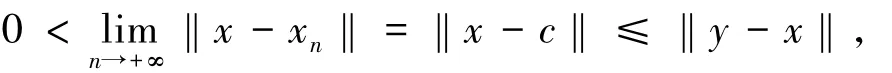
結合該式與(14)式易得

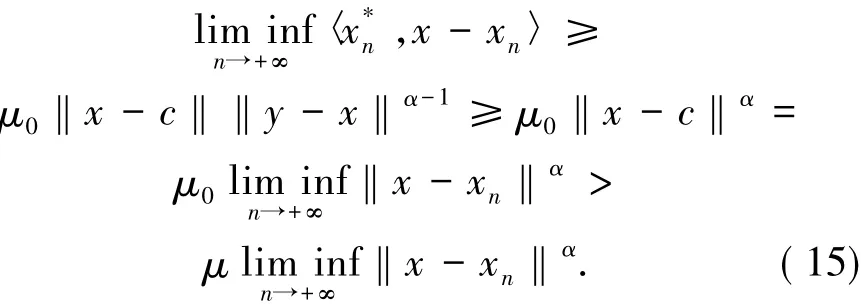
由(15)式，總可以找到μ2＞μ1＞μ0使得

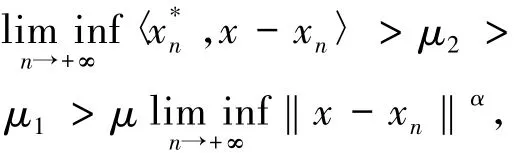
這意味著當n充分大時

此時顯然有如下式子成立

又因為?f是廣義松弛μ擬單調映射，故對任意的x*∈?f(x)，當n充分大時〈x*，x－xn〉≥0.取極限n→+∞，則有

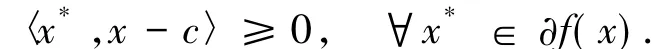
因此

故由定義知f是廣義松弛μ擬凸函數.

命題6假設?是使得?f(x)???f(x)(參見文獻［17］)成立的任何次微分，其中

如果f是廣義松弛μ擬凸函數，則?f是廣義松弛μ擬單調的.

證明顯然，只需證明??f是廣義松弛μ擬單調的.假設x，y∈X，存在x*∈??f(x)使得〈x*，y－x〉＞0，去證明

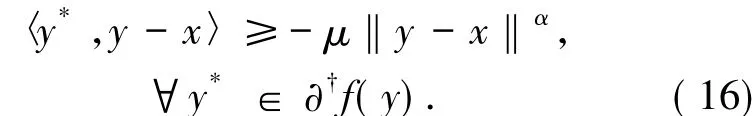
上述假設條件蘊含對任意w∈X充分趨近于y時有〈x*，w－x〉＞0成立.根據函數f的松弛μ擬凸性，易得

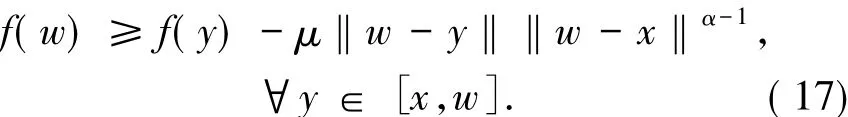
由(17)式，取y:=w+t(x－w)，?t∈［0，1］可以推出

根據(18)式，取v:=x－y且根據?f的定義，對任意的y*∈??f(y)有下式成立

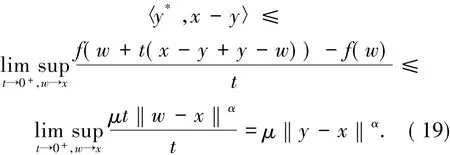
顯然，(19)式蘊含(16)式.這意味著??f是廣義松弛μ擬單調的.

［1］COTTLE R W，YAO J C.Pseudomonotone complementarity problems in Hilbert spaces［J］.J Optim Theory Appl，1992，78:281－295.

［2］YAO J C.Multivalued variational inequalities with K－Pseudomonotone operators［J］.J Optim Theory Appl，1994，83:391－403.

［3］CROUZEIX J P.Pseudomonotone variational inequality problems:existence of solutions［J］.Math Program，1997，78:305－314.

［4］HADJISAWAS N，SCHAIBLE S.Quasimonotone variational inequalities in Banach spaces［J］.J Optim Theory Appl，1996，90:95－111.

［5］AUSSEL D，HADJISAWAS N.On quasimonotone variational inequalities［J］.J Optim Theory Appl，2004，121:445－450.

［6］DANIILIDIS A，HADJISAWAS N.On the subdifferentials of pseudoconvex and quasiconvex functions and cyclic monotonicity［J］.J Math Anal Appl，1999，237:30－42.

［7］FAROUQ N L.Convergent algorithm based on progressive regularization for solving pseudomonotone variational inequalities［J］.J Optim Theory Appl，2004，120:455－485.

［8］KONNOV I V.Partial proximal point method for nonmonotone equilibrium problems［J］.Optim Methods Soft，2006，21:373－384.

［9］BAI M R.On generalized monotonicity of variational inequalities［J］.Comput Math Appl，2007，53:910－917.

［10］何詣然.具有集值映射變分不等式的理論分析［J］.四川師范大學學報(自然科學版)，2010，33(6):840－848.

［11］FANG Y P，HUANG N J.Variational－like inequalities with generalized monotone mappings in Banach spaces［J］.J Optim Theory Appl，2003，118:327－338.

［12］BAI M R，ZHOU S Z，NI G Y.Variational－like inequalities with relaxed η－α pseudomonotone mappings in Banach spaces［J］.Appl Math Lett，2006，19:547－554.

［13］BAI M R，HADJISAWAS N.Relaxed quasimonotone operators and relaxed quasiconvex functions［J］.J Optim Theory Appl，2008，138:329－339.

［14］CHEN L.Relaxed η－α quasimonotone and application to the generalized variational－like inequality problem［J］.J Ineq Appl，2013，2013:488.

［15］FAN K.A generalization of Tychonoff’s fixed point theorem［J］.Math Ann，1961，142:305－310.

［16］AUSSEL D，CORVELLEC J N，LASSONDE M.Mean value property and subdifferential criteria for lower semicontinuous functions［J］.Trans Am Math Soc，1995，347:4147－4161.

［17］PENOT J P.Are generalized derivatives useful for generalized convex functions［C］//CROUZEIX J P，MARTíNEZ－LEGAZ J E，VOLLE M.Generalized Convexity，Generalized Monotonicity.Dordrecht:Kluwer Academic，1998:3－59.

［18］王敏，周密.擬單調映射對偶平衡問題解的存在性［J］.四川師范大學學報(自然科學版)，2008，31(2):138－140.

［19］付冬梅，何詣然.廣義混合變分不等式的Tikhonov正則化方法［J］.四川師范大學學報(自然科學版)，2014，37(1):12－17.

［20］邱丹，邱濤，何詣然.一類二次投影算法的擾動分析［J］.四川師范大學學報(自然科學版)，2010，33(6):741－743.

Generalized Relaxed Quasimonotone Mappings and Generalized Relaxed Quasiconvex Functions

PU Sisi，HE Yiran
(College of Mathematics and Software Science，Sichuan Normal University，Chengdu 610066，Sichuan)

In this paper，we introduce a broader class of multivalued generalized relaxed quasimonotone mappings in normed spaces.Using the KKM technique，the existence of solutions of variational inequalities for such operators is established.Furthermore，it is proved that the subdifferential of generalized relaxed μ quasiconvex functionis generalized relaxed μ quasimonotone.

variational inequalities;generalized relaxed quasimonotone operators;generalized relaxed quasiconvex functions; subdifferentials

O177.92;O22

A

1001－8395(2016)03－0337－07

10.3969/j.issn.1001－8395.2016.03.007

(編輯李德華)

2015－04－15

國家自然科學基金(11271274)

*通信作者簡介:何詣然(1973—)，男，教授，主要從事非線性規劃領域的研究，E－mail:yrhe@sicnu.edu.cn

2010 MSC:58E35