黎曼流形上的廣義向量似變分不等式和向量優化問題

陳勝蘭，方長杰

黎曼流形上的廣義向量似變分不等式和向量優化問題

陳勝蘭，方長杰

(重慶郵電大學理學院，重慶400065)

利用黎曼流形上廣義次微分的概念，定義Minty型和Stampcchia型的廣義(弱)向量似變分不等式，并在不變凸性的假設下建立向量優化問題與廣義弱向量似變分不等式的等價關系.方法和結果是新的，且推廣了這一領域內許多已知結果.

黎曼流形;廣義向量似變分不等式;不變凸函數;向量優化

基于黎曼流形上的變分不等式首先是由S.Z.Németh［1］提出來的.在文獻［1］中，S.Z.Németh研究了Hadamard流形上的變分不等式解的存在性等問題.本文的目的是研究黎曼流形上非可微向量優化問題和廣義弱向量似變分不等式解的等價性.本文的方法和結果是新的，所得結論推廣了文獻［2－3］中的相應結果.

1 預備知識

文中有關黎曼流形的概念，如黎曼流形M上的局部Lipschitz函數、切空間TxM、切叢TM、余切空間TxM*、坐標卡、平行轉移等可參見文獻［4－ 11］.

定義1.1［9］設函數f:M→R在點x∈M附近滿足局部Lipschitz條件，(U，φ)是包含點x的坐標卡，則f在點x處沿方向v∈TxM的廣義方向導數定義為

定義1.2［9］設函數f:M→R在點y∈M附近滿足局部Lipschitz條件，點y的余切空間TyM*的子集

稱為函數f在點y的廣義次微分.

引理1.1［9］設M為有限維黎曼流形，x，y∈M，γ:［0，1］→M是一連結x和y的光滑曲線.設f在γ［0，1］上是局部Lipschitz的，則存在0＜t0＜1和ξ∈?f(γ(t0))使得

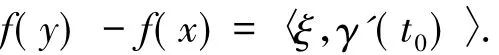
引理1.2［9］設函數f:M→R在點x∈M附近滿足局部Lipschitz條件，則有:

(i)?cf(x)是TxM*的非空凸緊子集，且對任意的ξ∈?cf(x)，有‖ξ‖*≤K，其中K為Lipschitz常數;

(ii)設{xi}和{ξi}分別是M和TxM*中的2個序列，且ξi∈?cf(xi).若{xi}收斂于x，且{(ξi)}收斂于ξ(其中，γ(ti)=xi，γ(t)=x)，則有ξ∈?cf (x).

定義1.3［5］設K為M的非空子集，η:M×M→TM為一向量值函數，且對任意的x，y∈M有η(x，y)∈TyM.若對任意的x，y∈K，存在唯一的測地線γ:［0，1］→M使得

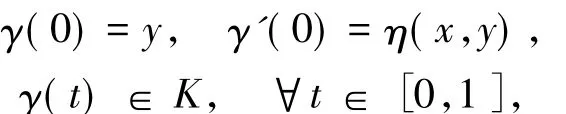
則稱K關于η為不變凸集.

注1.1在上述定義中，考慮γ(t)，γ(u)∈K，并定義

β(s)=γ((1－s)u+st)，?s，u，t∈［0，1］，則β是連接γ(u)和γ(t)的唯一測地線，且有現在給出黎曼流形上定義在開不變凸集上的不變凸函數的定義.

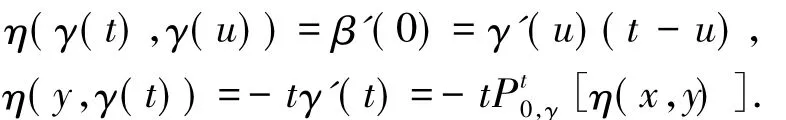
定義1.4［5］設K關于η為不變凸集，f是K上的局部Lipschitz函數，如果對任意的x，y∈K有

則稱f在K上是關于η的不變凸函數.由上述定義不難證明下述引理.

引理1.3設K關于η為不變凸集，f是K上的局部Lipschitz函數.若f在K上關于η為不變凸函數，則對任意的x，y∈K，有如下不等式成立

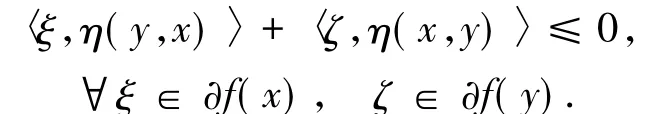
定義1.5［5］設K關于η為不變凸集，f是K上的實值函數，若對任意的x，y∈K有

f(γ(t))≤tf(x)+(1－t)f(y)，?t∈［0，1］，則稱f關于η是預不變凸函數，其中γ是定義1.3中的唯一測地線.

引理1.4設K關于η為不變凸集，f是K上的局部Lipschitz函數.若f是關于η的不變凸函數，則f亦為關于η的預不變凸函數.

證明類似文獻［5］中的定理4.2可證.

設K為M的非空子集，f:K→Rp為一向量值函數，且f=(f1，f2，…，fp).下面考慮黎曼流形M上的向量優化問題(VOP)

定義1.6［12］設珋x∈K，則有:

(i)如果對?x∈K有

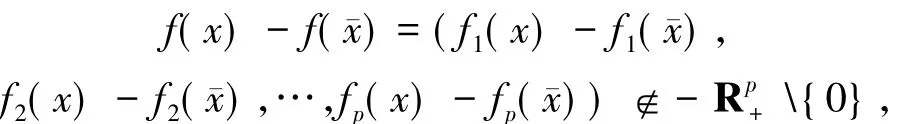
則稱珋x∈K為(VOP)的有效解;

(ii)如果對?x∈K有

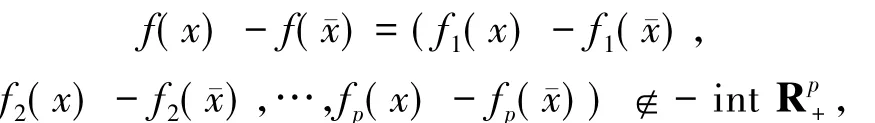
則稱珋x∈K為(VOP)的弱有效解.

類似于歐氏空間關于向量(似)變分不等式的定義(可參見文獻［13－16］)，下面引入黎曼流形上廣義向量變分不等式的概念.

定義1.7設fi(i∈J={1，2，…，p})在K上是局部Lipschitz函數，則有:

(i)Minty型廣義向量似變分不等式(GMVVLIP)是指尋找x∈K，使對?y∈K和ξi∈?fi(y)(i∈J)有

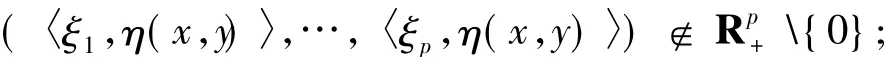
(ii)Stampacchia型廣義向量似變分不等式(GSVVLIP):尋找x∈K，使存在ξi∈?cfi(x)(i∈J)，且對?y∈K有

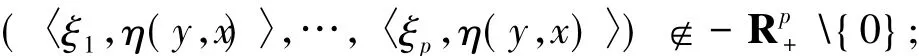
(iii)Minty型廣義弱向量似變分不等式(GWMVVLIP)是指尋找x∈K，使對?y∈K和ξi∈?fi(y)(i∈J)有

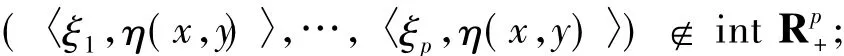
(iv)Stampacchia型廣義弱向量似變分不等式(GWSVVLIP):尋找x∈K，使存在ξi∈?cfi(x)(i∈J)，且對?y∈K有

注1.2若M=Rn，則上述定義為文獻［2－3］中所討論的Minty型和Stampcchia型向量變分不等式.

2 主要結果

下面主要討論黎曼流形上廣義向量變分不等式和向量優化問題的等價關系.

定理2.1設M為有限維黎曼流形，K?M關于η為不變凸集.對?i∈J，fi:K→R在K上是局部Lipschitz的，且為關于η的不變凸函數，則x∈K是(VOP)的有效解當且僅當x亦是(GMVVLIP)的解.

證明設x∈K是(GMVVLIP)的解，但x不是(VOP)的解，則存在y∈K使得即有

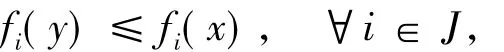
且在某個k∈J處取嚴格不等式.

因K關于η為不變凸集，則存在唯一測地線γ:［0，1］→M使得

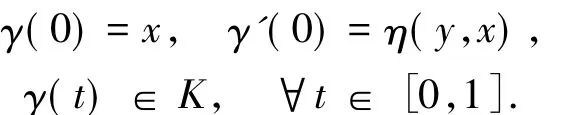
由引理1.4，每個fi(i∈J)關于η是預不變凸函數，故有

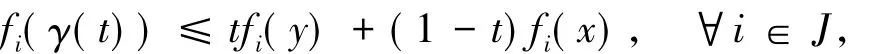
即

現定義β:［0，1］→M如下

由引理1.1知，存在li∈(0，t)和ξi∈?cfi(β(li))使得

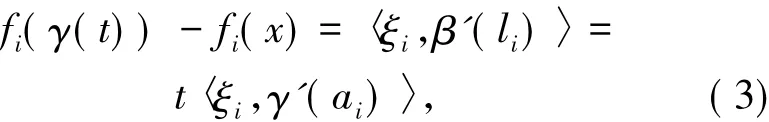
其中，ai=lit＜t，zi=γ(ai).

結合(1)～(3)式，對?i∈J有

且在某個k∈J處取嚴格不等式.現取t0∈(0，1)使對任意的i∈J有t0＜ai.由注1.1知

及

由(4)和(5)式可得

且在某個k∈J處取嚴格不等式.因fi關于η為不變凸函數，由引理1.3可知

且在某個k∈J處取嚴格不等式.又η(x，γ(t0))= (－t0)γ'(t0)，由(6)和(7)式可得

且在某個k∈J處取嚴格不等式.因此，對所有ζi0∈?cfi(γ(t0))(i∈J)有

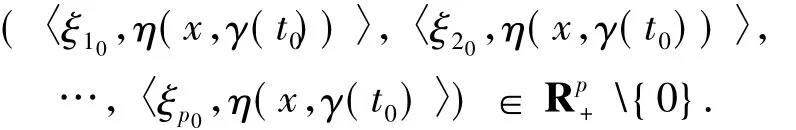
而這與x是(GMVVLIP)的解矛盾.

反之，若x是(VOP)的解但不是(GMVVLIP)的解，則存在y∈K及ξi∈?cfi(y)(i∈J)使得

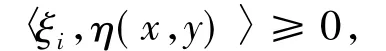
且在某個k∈J處取嚴格不等式.由fi關于η的不變凸性，可知

且在某個k∈J處取嚴格不等式，即有

而這與x是(VOP)的有效解矛盾.證畢.

定理2.2設M為有限維黎曼流形，K?M關于η為不變凸集.對?i∈J，fi:K→R在K上是局部Lipschitz的，且關于η是不變凸函數.若x∈K是 (GSVVLIP)的解，則x為(VOP)的有效解，且亦是(GMVVLIP)的解.

證明因x∈K是(GSVVLIP)的解，對任意的y∈K，存在ξi∈?cfi(x)(i∈J)使得

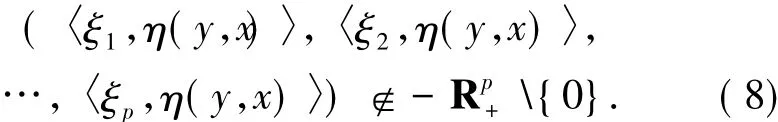
由于每個fi關于η是不變凸函數，所以

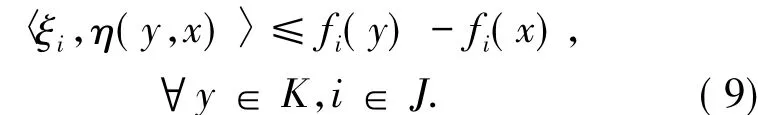
由(8)和(9)式可得

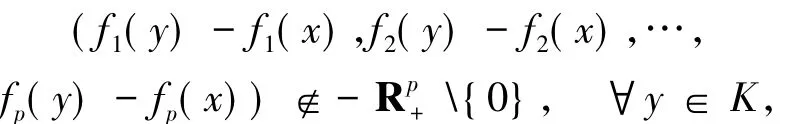
這表明x是(VOP)的有效解.由定理2.1知，x亦為(GMVVLIP)的解.證畢.

定理2.3設K?M關于η為不變凸集.對?i∈J，fi:K→R在K上是局部Lipschitz的，且關于η是不變凸函數.如果x∈K是(GWSVVLIP)的解，那么x亦是(GWMVVLIP)的解.

證明設x∈K是(GWSVVLIP)的解，但x不是(GWMVVLIP)的解，則存在y∈K和ξi∈?fi(y)(i∈J)使得

即

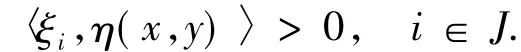
又fi關于η為不變凸函數，由引理1.3有

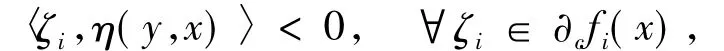
而這與x是(GWSVVLIP)的解矛盾.證畢.

定理2.4設K?M關于η為不變凸集.對?i∈J，fi:K→R在K上是局部Lipschitz的，且關于η是不變凸函數.如果x∈K是(GWMVVLIP)的解，那么x亦是(GWSVVLIP)的解.

證明設x∈K是(GWMVVLIP)的解.設y∈K和{tm}↘0且tm∈(0，1］，因K?M關于η為不變凸集，則存在唯一測地線γ:［0，1］→M使得

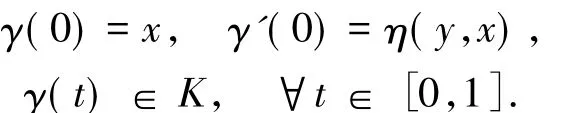
又x∈K是(GWMVVLIP)的解，所以對ξm

i∈?cfi(γ(tm))(i∈J)有

由注1.1知

又fi(i∈J)為局部Lipschitz的，由引理1.1(ii)知存在k＞0，當m充分大時有

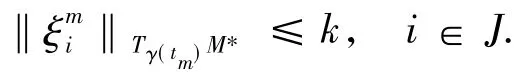
故

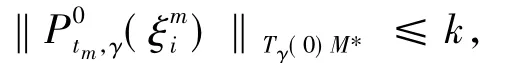
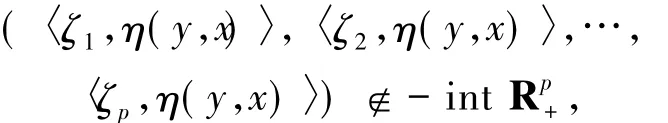
故x是(GWSVVLIP)的解.證畢.

由定理2.3和2.4有如下結論.

定理2.5設K?M關于η為不變凸集.對?i∈J，fi:K→R在K上是局部Lipschitz的，且關于η是不變凸函數，則x∈K是(GWMVVLIP)的解當且僅當x是(GWSVVLIP)的解.

定理2.6設K?M關于η為不變凸集.對?i∈J，fi:K→R在K上是局部Lipschitz的，且關于η是不變凸函數.如果x∈K是(GWSVVLIP)的解，則x是(VOP)的弱有效解.

證明設x∈K是(GWSVVLIP)的解但不是(VOP)的弱有效解，則存在y∈K使得

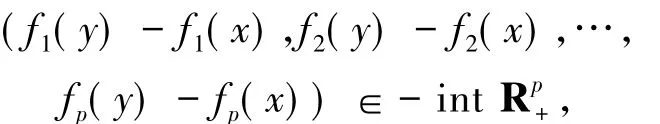
上式等價于

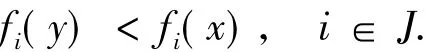
由于fi(i∈J)關于η是不變凸的，所以

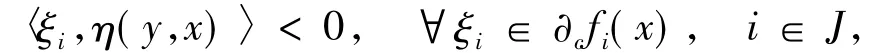
即有

而這與x是(GWSVVLIP)的解矛盾.證畢.

定理2.7設K?M關于η為不變凸集.對?i∈J，fi:K→R在K上是局部Lipschitz的，且關于η是不變凸函數.如果x∈K是(VOP)的弱有效解，那么x是(GWMVVLIP)的解.

證明設x∈K是(VOP)的弱有效解但不是(GWMVVLIP)的解，則存在y∈K和ξi∈?cfi(y)(i∈J)使得

即對?i∈J有

由fi(i∈J)關于η的不變凸性知

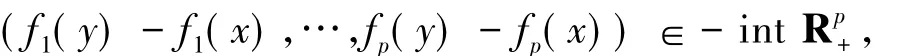
而這與x是(VOP)的弱有效解矛盾.證畢.

由定理2.5～2.7可得到下述結果.

定理2.8設K?M關于η為不變凸集，對?i∈J，fi:K→R在K上是局部Lipschitz的，且關于η是不變凸函數，則x∈K是(VOP)的弱有效解當且僅當x是(GWSVVLIP)的解.

注2.1定理2.1～2.8將歐氏空間中的相關結論(如文獻［2，3］)推廣到了黎曼流形上.

致謝重慶郵電大學博士啟動基金項目(A2015－19)對本文給予了資助，謹致謝意.

［1］NéMETH S Z.Variational inequalities on Hadamard manifolds［J］.Nonlinear Anal，2003，52:1491－1498.

［2］Al－HOMIDIAN S，ANSARI Q H.Generalized Minty vector variational－like inequalities and vector optimization problems［J］.J Optim Theory Appl，2010，144:1－11.

［3］ANSARI Q H，YAO J C.On nondifferentiable and nonconvex vector optimization problems［J］.J Optim Theory Appl，2000，106(3):475－488.

［4］AZAGRA D，FERRERA J，LOPEZ－MESAS F.Nonsmooth analysis and Hamilton－Jacobi equations on Riemannian manifolds［J］.J Funct Anal，2005，220:304－361.

［5］BARANI A，POURYAYEVALI M R.Invex sets and preinvex functions on Riemannian manifolds［J］.J Math Anal Appl，2007，328:767－779.

［6］CHAVEL I.Riemannian Geometry:a Modern Introduction［M］.Cambridge:Cambridge University Press，1993.

［7］RAPSCáK T.Smooth Nonlinear Optimization in Rn［M］.Dordrecht:Kluwer Academic Publishers，1997.

［8］SAKAI T.Riemannian geometry［C］//Translations of Mathematical Monographs，149.Providence:American Mathematical Society，1996.

［9］HOSSEINI S，POURYAYEVALI M R.Generalized gradients and characterization of epi－Lipschitz sets in Riemannian manifolds［J］.Nonlinear Anal，2011，74:3884－3895.

［10］UDRISTE C.Convex Functions and Optimization Methods on Riemannian Manifolds:Mathematics and Its Applications［M］.Dordrecht:Kluwer Academic Publishers，1994:297.

［11］唐國吉，汪星，夏福全.Hadamard流形上極大單調向量場奇點的Mann迭代算法［J］.四川師范大學學報(自然科學版)，2015，38(6):818－823.

［12］ANSARI Q H，YAO J C.Recent Developments in Vector Optimization［M］.New York:Springer－Verlag，2012.

［13］GIANNESSI F.On Minty variational principle［C］//New Trends in Mathematical Programming.GIANNESSI F，KOMLOSI S，TAPCSACK T.Dordrechet:Kluwer Academic，1998:93－99.

［14］GIANNESSI F.Theorems of alternative，ratic programs and complementary problems［C］//Variational Inequality and Complementary Problems.COTTLE R W，GIANNESSI F，LIONS J C.New York:John Wiley＆Sons，1980.

［15］MISHRA S K，WANG S Y.Vector variational－like inequalities and nonsmooth vector optimization problems［J］.Nonlinear Anal，2006，64:1939－1945.

［16］YANG X M，YANG X Q，TEO K L.Some remarks on the Minty vector variational inequality［J］.J Optim Theory Appl，2004，121:193－201.

Generalized Vector Variational-like Inequality and Vector Optimization Problem on Riemannian Manifolds

CHEN Shenglan，FANG Changjie
(College of Science，Chongqing University of Posts and Telecommunications，Chongqing 400065)

In this paper，we introduce a Minty type vector variational inequality，a Stampacchia type vector variational inequality，and the weak forms of them，which are all defined by means of generalized subdifferentials on Riemannian manifolds.We also establish a relationship between generalized vector variational-like inequalities and nonsmooth vector optimization problems on Riemannian manifolds under the assumption of invexity or invariant monotonicity.Our approach and results are new and generalize many known results in this field.

Riemannian manifold;generalized vector variational-like inequality;invex functions;vector optimization problem

O186.12;O224

A

1001－8395(2016)03－0332－05

10.3969/j.issn.1001－8395.2016.03.006

(編輯李德華)

2015－03－13

國家自然科學基金(11426055)和重慶市教委科研項目(KJ070514)

陳勝蘭(1981—)，女，講師，主要從事優化理論及應用的研究，E－mail:chensl@cqupt.edu.cn

2010 MSC:53C25;26D20;58E35