一種基于熵增理論的疲勞-蠕變交互作用損傷模型及試驗驗證

陳　凌　張賢明　劉　飛　歐陽平　劉先斌

1.重慶工商大學廢油資源化技術與裝備教育部工程研究中心，重慶,4000672.重慶大學，重慶,400044

?

一種基于熵增理論的疲勞-蠕變交互作用損傷模型及試驗驗證

陳凌1,2張賢明1劉飛2歐陽平1劉先斌1

1.重慶工商大學廢油資源化技術與裝備教育部工程研究中心，重慶,4000672.重慶大學，重慶,400044

摘要：根據經典熱力學理論，材料疲勞-蠕變交互作用下的損傷過程可視為系統熵增的累積，當熵增積累到臨界值時，材料發生失效斷裂。按此理論，并基于連續損傷力學和能量守恒定律，以系統熵增的變化來描述材料損傷，建立了一種疲勞-蠕變交互作用的損傷模型。為驗證該模型，進行了540℃和520℃環境下1.25Cr-0.5Mo鋼應力控制的梯形波加載試驗，以材料的殘余應變反映熵增積累，選取殘余應變的變化作為損傷變量，用上述損傷模型進行了材料疲勞-蠕變交互作用的損傷演化描述，結果表明實測損傷點數據與該模型的損傷演化規律符合較好。

關鍵詞：疲勞-蠕變；熵增；連續損傷力學；損傷變量；殘余應變

0引言

石油化工、冶金、動力、航空航天等領域的高溫承壓設備在服役過程中通常承受疲勞和蠕變的交互作用，容易引發設備失效，疲勞-蠕變交互作用的損傷演化規律是這類設備進行安全評估的重要依據，一直以來受到國內外工程研究人員的關注。到目前為止，許多學者針對疲勞-蠕變交互作用的損傷演化進行了研究[1-9]，這類研究主要是基于經典的連續損傷力學(continuum damage mechanics，CDM)[10]理論，利用材料有效承載面積的減少定義損傷，分別計算疲勞和蠕變的損傷后進行疊加，再基于相應的假設建立損傷模型，結合合適的損傷變量對損傷演化進行描述。這類模型由于需要分別計算疲勞和蠕變的損傷再進行疊加，大都形式復雜，需要的參數較多，不便于實際應用，同時，一些基于相應假設的簡化模型缺乏足夠的理論基礎。

針對上述情況，本文根據經典熱力學理論，將材料疲勞-蠕變交互作用下的損傷過程視為系統熵增的累積，當熵增積累到臨界值時，材料發生失效斷裂。按此理論，并基于連續損傷力學和能量守恒定律，以系統熵增的變化來描述材料損傷，建立了一種疲勞-蠕變交互作用的損傷模型。為驗證模型的準確性，進行了540℃和520℃環境下1.25Cr0.5Mo鋼應力控制的梯形波加載試驗，以材料的殘余應變反映熵增積累，選取殘余應變的變化作為損傷變量，用上述損傷模型進行了材料疲勞-蠕變交互作用的損傷演化描述。

1一種基于熵增理論的疲勞-蠕變交互作用損傷模型

根據經典熱力學理論，熵是表征系統無序混亂程度的狀態量，材料疲勞-蠕變交互作用下的損傷過程可視為系統熵增的積累，當熵增積累到臨界值時，材料發生失效斷裂。按此理論，材料疲勞-蠕變交互作用下的損傷可定義為

(1)

式中，D為材料損傷；ΔS為材料疲勞-蠕變交互作用過程中的單位質量熵增積累；ΔSf為材料疲勞-蠕變交互作用下失效破壞時的單位質量熵增積累臨界值。

同時，根據經典熱力學理論，物質的熵增定義為

(2)

式中，s為物質的單位質量熵；q為單位質量物質與外部環境之間的熱量交換；T為絕對溫度。

另外，對于金屬材料等連續致密材料，其疲勞-蠕變交互作用的過程滿足自然界的普遍定律——能量守恒定律[11]，即物體內能和動能的增量之和等于物體接受的熱增量與作用于物體的機械功的增量之和。根據經典熱力學理論，能量守恒定律的局部表達式可表示為[12]

(3)

將式(2)代入式(3)中物體與外界的熱量交換變化率(hi,i-ργ)，可得如下關系式：

(4)

將式(4)代入式(3)，可得

(5)

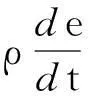
(6)

式中，W為機械功；ηW為機械功的內能轉化率。

對于承受疲勞-蠕變交互作用的材料來說，每一循環過程中的彈性變形是可恢復的，而塑性變形是不可恢復的。因此，可認為材料每一循環過程中的熵增同材料的塑性變形相關，當塑性變形累積到一定程度時，材料的熵增積累達到臨界值，材料即發生失效斷裂。按此理論，根據式(6)，材料疲勞-蠕變交互作用下每一循環過程的熵增可表示為

(7)

式中，Δs為每一循環過程的單位質量熵增；Δtn為疲勞-蠕變交互作用下每一循環過程的時間；σeq為等效應力，與加載應力相關；Δεp為塑性應變范圍。

對于疲勞-蠕變交互作用的加載過程來說，其塑性階段的應力-應變曲線是非線性的。同時，對于金屬材料等工程材料，其塑性階段的應力-應變曲線大都符合冪強化力學模型[13]。因此，式(7)中的函數f(σeq,Δεp)可定義如下：

(8)

式中，m、 a、b為材料常數。

將式(8)代入式(7)，可得材料疲勞-蠕變交互作用下每一循環過程的單位質量熵增：

(9)

如前所述，材料疲勞-蠕變交互作用下的損傷過程可視為系統熵增的積累，因此，利用式(9)，對材料每一循環過程的單位質量熵增進行積分，可得材料疲勞-蠕變交互作用過程中的單位質量熵增積累：

(10)

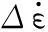
當循環周次N達到材料的失效壽命Nf時，ΔS即為ΔSf。

另外，基于式(1)，材料疲勞-蠕變交互作用下的損傷演化方程可定義如下：

(11)

將式(10)代入式(11)，可得

(12)

根據變上限定積分求導法則[14]，式(12)可改寫為

(13)

根據經典損傷力學理論[10]，材料的損傷會導致有效承載面積減小使得應力增大。考慮到損傷對應力的影響，將式(13)改寫為

(14)

對式(14)求積分，取積分上下限為D|N=0=D0，D|N=Nf=1，可得

D=1-(1-D0)(1-N/Nf)1/(a+1)

(15)

式中，D0為初始損傷。

對于材料疲勞-蠕變交互作用下的損傷演化，其損傷累積與加載應力和溫度相關，因此，可用函數k(σ,T)代替式(15)中的1/(a+1)，將式(15)改寫為

D=1-(1-D0)(1-N/Nf)k(σ,T)

(16)

其中，k(σ,T)為加載應力和溫度的函數(簡寫為k)，用來反映疲勞-蠕變交互作用下的損傷累積程度。

式(16)即為基于熵增理論推導出的一種疲勞-蠕變交互作用損傷模型，該模型形式簡單，理論依據明確，不需要大量的純蠕變或純疲勞試驗來確定相關參數，非常便于實際應用。

2損傷變量選取

根據連續損傷力學，損傷變量是一種用于描述材料內部損傷狀態變化發展及其對材料力學作用影響的內部狀態變量[10]。如前所述，材料疲勞-蠕變交互作用下的損傷過程可視為系統熵增的積累，同時材料每一循環過程中的熵增同材料的塑性變形相關，當塑性變形累積到一定程度時，材料的熵增積累達到臨界值，材料即發生失效斷裂。材料每一循環的塑性變形積累會導致材料的殘余應變增大，因此，可用材料的殘余應變反映熵增積累。定義損傷變量為

(17)

式中，εrN為材料第N次循環后的殘余應變；εrf為材料失效斷裂時的殘余應變。

式(17)所示的損傷變量，相比已有的選取彈性模量、割線模量及應變能密度等的變化作為損傷變量[15-18]來說，工程測量更為方便，具有較好的實時性，應用方便。

3試驗結果及討論

試驗在島津電液伺服疲勞試驗機上進行，試驗溫度為540 ℃和520 ℃，采用螺紋夾持的1.25Cr0.5Mo珠光體耐熱鋼光滑圓棒試樣，試樣按國家標準GB/T15248-2008[19]制作。試驗控制方式采用應力控制，為引入蠕變保載,采用梯形波加載，上下保載時間各為5s，加載頻率0.05Hz。具體的試驗條件及試驗結果見表1、表2，其中Δσ為應力范圍，σa為應力幅，σm為平均應力。

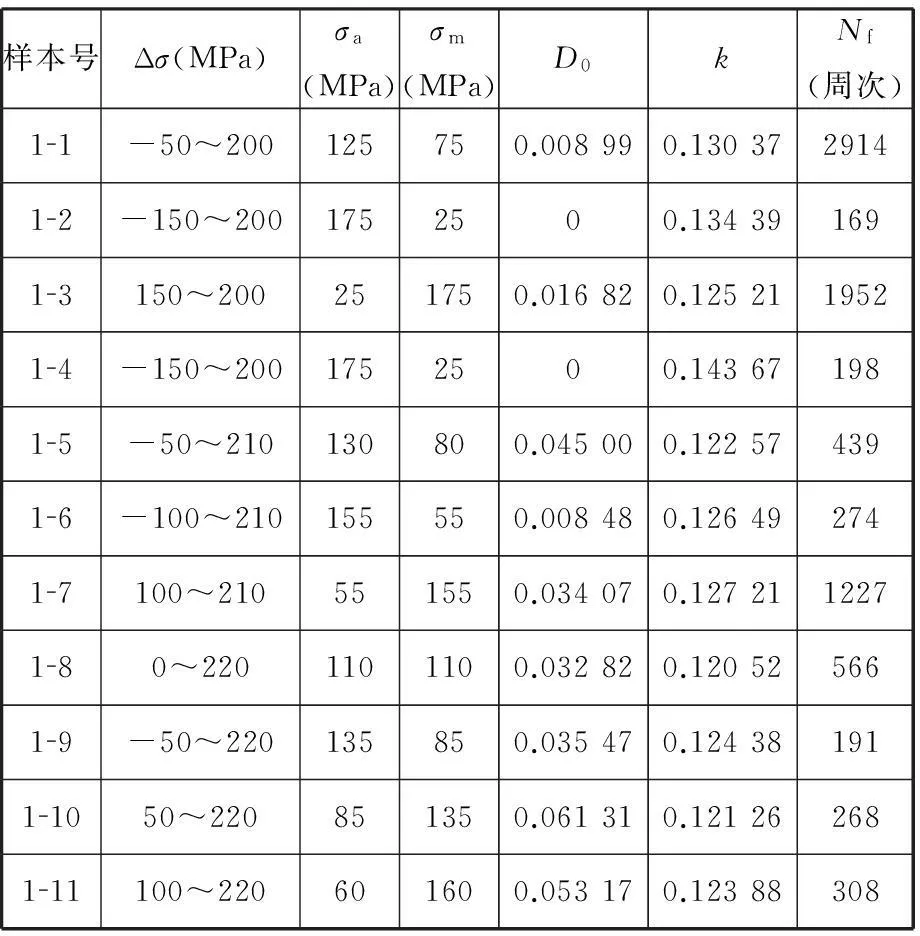
表1　540 ℃下材料疲勞-蠕變交互作用試驗數據表

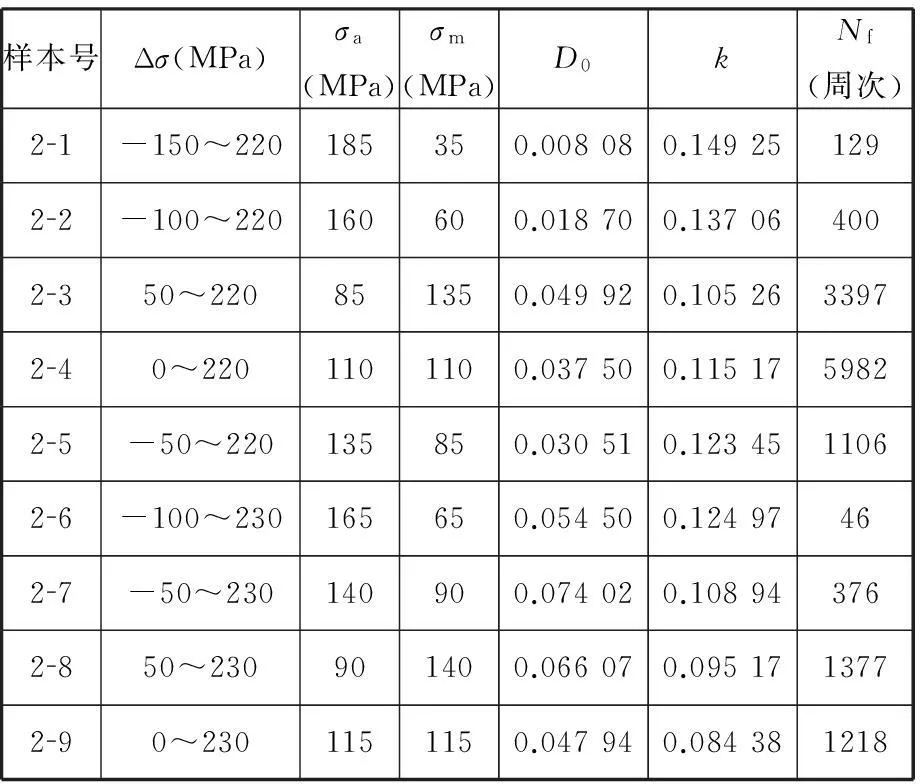
表2　520 ℃下材料疲勞-蠕變交互作用試驗數據表

圖1、圖2分別為根據試驗結果按式(17)所定義的損傷變量求得的1.25Cr0.5Mo鋼在540 ℃和520 ℃環境下疲勞-蠕變交互作用下材料損傷的變化曲線，圖中壽命分數φ=N/Nf。由圖1、圖2可知，材料的損傷在約80%壽命段區間內的增大速率變化不大，在循環后期隨著塑性變形的積累導致材料的熵增積累逐漸接近臨界值，損傷快速增大，當熵增積累達到臨界值時，材料發生失效斷裂。

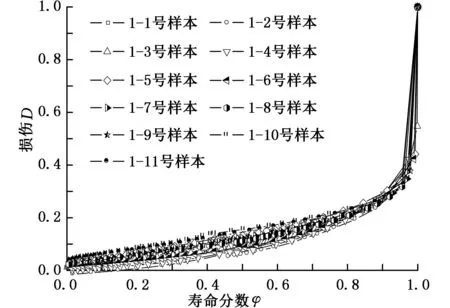
圖1　1.25Cr0.5Mo鋼540 ℃疲勞-蠕變交互作用下的損傷變化曲線

在式(16)所示損傷模型中，以壽命分數φ=N/Nf為橫軸、損傷D為縱軸，材料的損傷根據試驗結果按式(17)所定義的損傷變量進行計算，可擬合求得1.25Cr0.5Mo鋼在540 ℃和520 ℃環境下各樣本的損傷模型和損傷曲線，擬合圖見圖3、圖4(僅給出了代表性的擬合圖)，擬合結果見表1、表2。

圖2　1.25Cr0.5Mo鋼520 ℃疲勞-蠕變交互作用下的損傷變化曲線

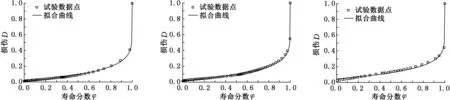
(a)1-1號樣本　　 　　　　　　　　(b)1-3號樣本　 　　　　　　　　　(c)1-5號樣本

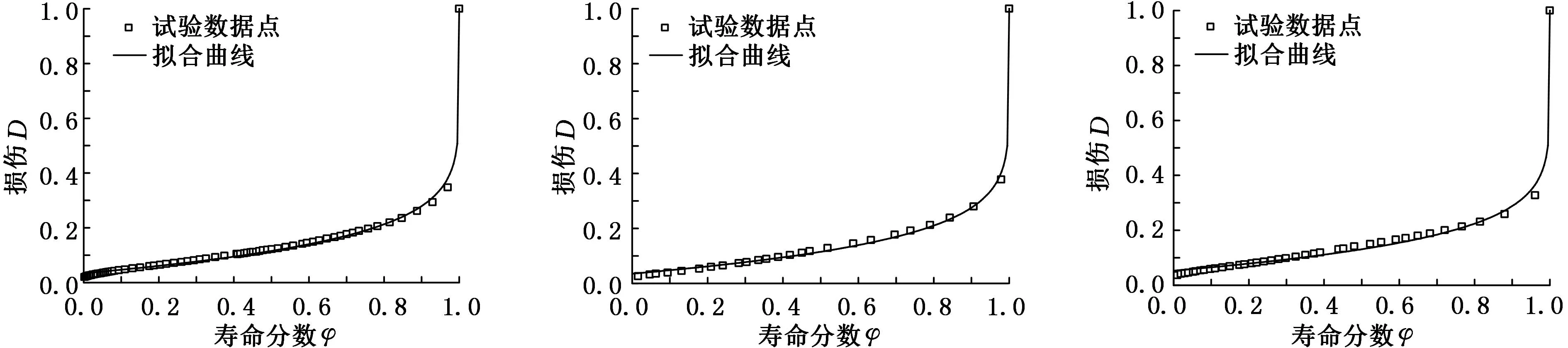
(d)1-7號樣本　　 　　　　　　　　(e)1-9號樣本　 　　　　　　　　　(f)1-11號樣本圖3　1.25Cr0.5Mo鋼540 ℃疲勞-蠕變交互作用損傷模型擬合圖

從圖3、圖4中可以看出，用材料的殘余應變反映熵增積累，選取材料殘余應變的變化作為損傷變量，按式(16)所示損傷模型擬合得到的損傷曲線與試驗實測損傷點數據的符合程度較好，能夠較好地描述材料的損傷演化。

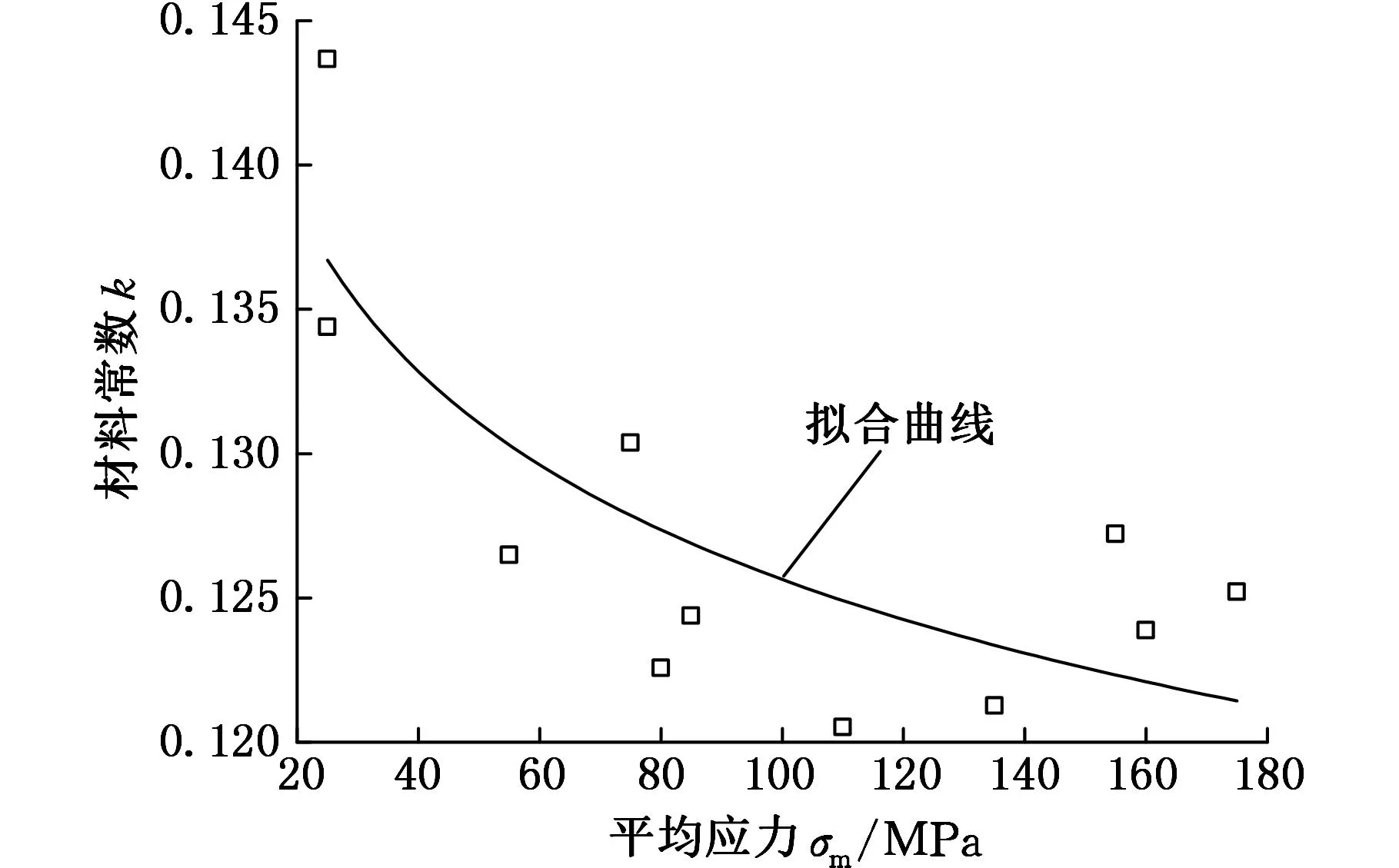
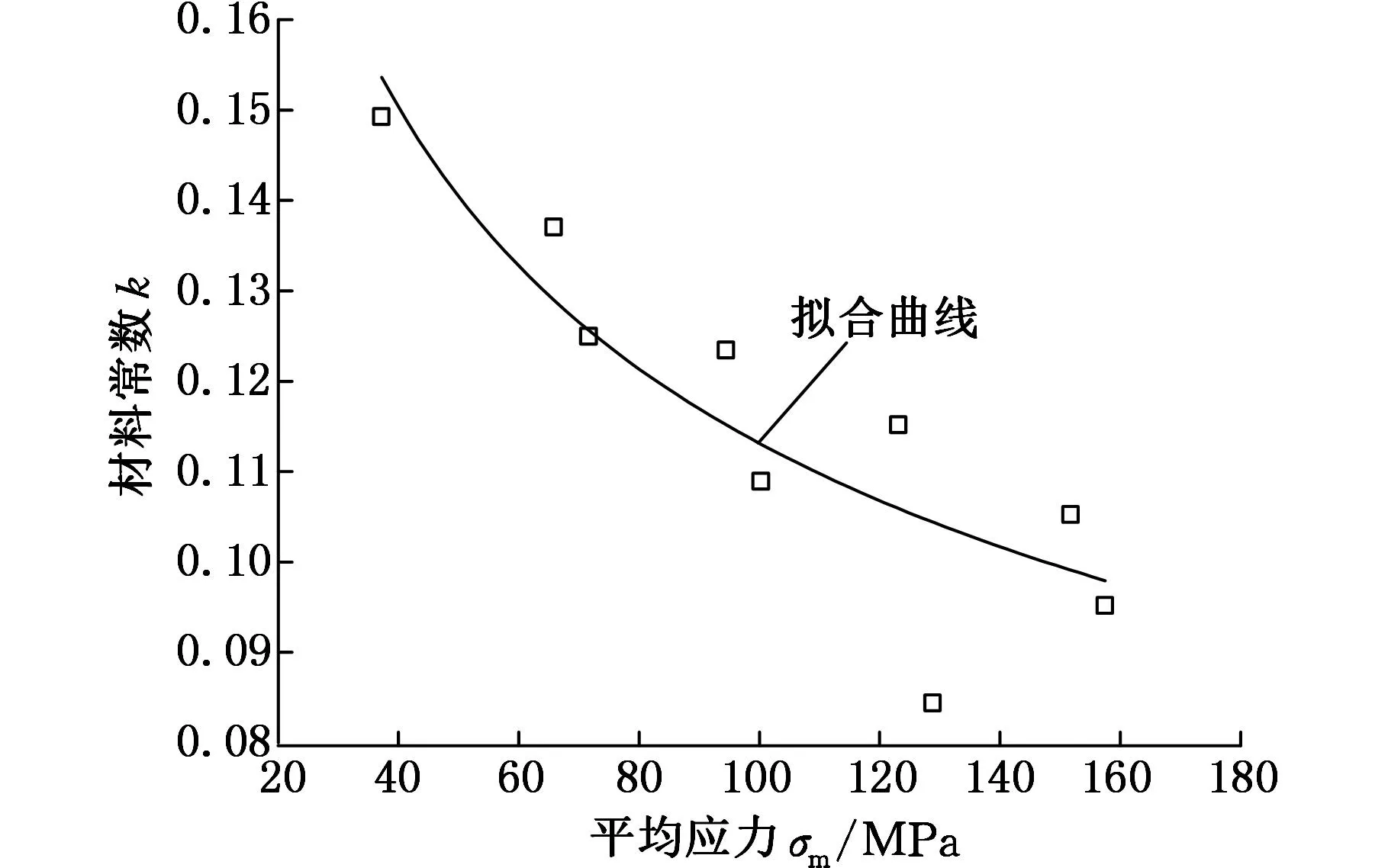
另外，如前所述，式(16)中的材料常數k為加載應力和溫度的函數，在一定的溫度下，k為加載應力的函數，與加載的最大應力、應力幅、保載時間等因素相關。由于加載的最大應力σmax、應力幅σa和平均應力σm具有σm=σmax-σa的關系，所以，當保載時間固定時，在最大應力相差不大的情況下，可用平均應力來反映最大應力和應力幅的影響，將k簡化為平均應力的函數。

圖5給出了1.25Cr0.5Mo鋼在540 ℃、520℃ 時各工況下k隨平均應力的變化趨勢。由圖5可知，材料常數k隨平均應力的增大而減小，其減小趨勢與冪函數形勢較為符合，用冪函數對其進行擬合，擬合曲線見圖5，擬合關系式如下：

540 ℃時

(18)

520 ℃時

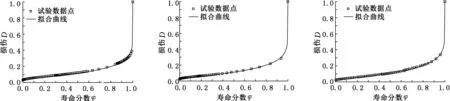
(a)2-3號樣本　　 　　　　　　　　(b)2-4號樣本　 　　　　　　　　　(c)2-5號樣本

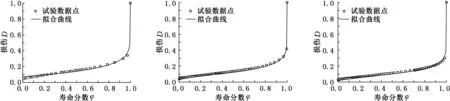
(d)2-7號樣本　　 　　　　　　　　(e)2-8號樣本　 　　　　　　　　　(f)2-9號樣本圖4　1.25Cr0.5Mo鋼在520 ℃疲勞-蠕變交互作用損傷模型擬合圖

(19)將式(18)、式(19)代入式(16)，即可得1.25Cr0.5Mo鋼在540 ℃、520 ℃環境下疲勞-蠕變交互作用的損傷模型如下：

540 ℃時

520 ℃時

(a)　溫度540℃

(b)溫度520℃圖5　k隨平均應力的變化及擬合圖

由上述分析可知，該損傷模型能夠較好地描述材料的損傷演化，同時該模型形式簡單，理論依據明確，具有較好的實際應用價值。

4結論

(1)根據經典熱力學理論，將材料疲勞-蠕變交互作用下的損傷過程視為系統熵增的積累，當熵增積累到臨界值時，材料發生失效斷裂。按此理論，并基于連續損傷力學和能量守恒定律，以系統熵增的變化來描述材料損傷，建立了一種疲勞-蠕變交互作用的損傷模型：

D=1-(1-D0)(1-N/Nf)k(σ,T)

該模型形式簡單，理論依據明確，不需要大量的純蠕變或純疲勞試驗來確定相關參數，非常便于實際應用。

(2)進行了540 ℃和520 ℃環境下1.25Cr-0.5Mo鋼應力控制的梯形波加載試驗，以材料的殘余應變反映熵增積累，選取殘余應變的變化作為損傷變量，用上述損傷模型進行了材料疲勞-蠕變交互作用的損傷演化描述，結果表明，試驗實測損傷點數據與該模型的損傷演化規律符合較好，該模型能夠較好地描述材料的損傷演化。

參考文獻：

[1]姚華堂, 軒福貞, 王正東, 等. 基于連續損傷理論的多軸蠕變設計[J]. 中國機械工程, 2007, 18(12):1439-1443.

YaoHuatang,XuanFuzhen,WangZhengdong,etal.MultiaxialCreepDesignBasedontheContinuumDamageTheory[J].ChinaMechanicalEngineering, 2007, 18(12):1439-1443.

[2]陳凌, 張賢明, 歐陽平. 一種疲勞-蠕變交互作用壽命預測模型及試驗驗證[J]. 中國機械工程, 2015, 26(10):1356-1361.

ChenLing,ZhangXianming,OuyangPing.AModelofLifePredictionforFatigue-creepInteractionandItsExperimentalVerification[J].ChinaMechanicalEngineering, 2015, 26(10):1356-1361.

[3]GharadaAE,ZedirabH,AzaribZ,etal.ASynergisticCreepFatigueFailureModelDamage(CaseoftheAlloyZ5NCTAat550℃) [J].EngineeringFractureMechanics, 2006, 73(6):750-770.

[4]朱順鵬, 黃洪鐘, 何俐萍, 等. 高溫低周疲勞-蠕變的改進型廣義應變能損傷函數方法[J]. 航空學報, 2011, 32(8):1445-1452.

ZhuShunpeng,HuangHongzhong,HeLiping,etal.ImprovedGeneralizedStrainEnergyDamageFunctionMethodforHighTemperatureLowCycleFatigue-creep[J].ActaAeronauticaetAstronauticaSinica, 2011, 32(8):1145-1452.

[5]胡緒騰, 馬曉健, 宋迎東. 含保載彈性應力循環下TA12鈦合金缺口試樣的蠕變疲勞損傷分析[J]. 機械工程材料, 2013, 37(3):90-94.

HuXuteng,MaXiaojian,SongYingdong.Creep-FatigueDamageAnalysisofTA12TitaniumAlloyNotchedSampleatElasticStressCyclewithDwellTime[J].MaterialsforMechanicalEngineering, 2013, 37(3):90-94.

[6]LeilaJL,AbhijitD.AMeso-scaleDamageEvolutionModelforCyclicFatigueofViscoplasticMaterials[J].InternationalJournalofFatigue, 2009, 31(4):703-711.

[7]SullivanRW.DevelopmentofaViscoelasticContinuumDamageModelforCyclicLoading[J].MechanicsofTime-DependentMaterials, 2008, 12(4):329-342.

[8]徐建剛, 許金余. 粉末冶金材料空穴和夾雜的疲勞蠕變損傷分析[J]. 熱加工工藝, 2013, 42(16):61-63,66.

XuJiangang,XuJinyu.AnalysisonFatigueandCreepDamageofPowderMetallurgyMaterialwithVoidandInclusion[J].HotWorkingTechnology, 2013, 42(16):61-63,66.

[9]WenJF,TuST.AMultiaxialCreep-damageModelforCreepCrackGrowthConsideringCavityGrowthandMicrocrackInteraction[J].EngineeringFractureMechanics, 2014, 123:197-210.

[10]沈為. 損傷力學[M]. 武漢: 華中理工大學出版社, 1995.

[11]楊光松. 損傷力學與復合材料損傷[M]. 北京: 國防工業出版社, 1995.

[12]ChenL,JiangJL,FanZC,etal.ANewModelforLifePredictionofFatigue-creepInteraction[J].InternationalJournalofFatigue, 2007, 29(4):615-619.

[13]畢繼紅. 工程彈塑性力學[M]. 天津: 天津大學出版社, 2003.

[14]吳迪光, 張彬. 微積分學(上)[M]. 杭州: 浙江大學出版社, 1995.

[15]LemaitreJ.AContinuousDamageMechanicsModelforDuctileFracture[J].JournalofEngineeringMaterialTechnology, 1985, 107(1):83-89.

[16]YangXH,LiN,JinZH,etal.AContinuousLowCycleFatigueDamageModelandItsApplicationinEngineeringMaterials[J].InternationalJournalofFatigue, 1997, 19(10):687-692.

[17]范志超, 蔣家羚, 陳學東. 16MnR鋼疲勞與循環蠕變交互作用損傷力學模型[J]. 浙江大學學報(工學版), 2006, 40(2):317-321.

FanZhichao,JiangJialing,ChenXuedong.ContinuumDamageMechanicsModelofInteractionbetweenFatigueandCyclicCreepof16MnRSteel[J].JournalofZhejiangUniversity(EngineeringScience), 2006, 40(2):317-321.

[18]DjebliA,AidA,BendoubaM,etal.ANon-linearEnergyModelofFatigueDamageAccumulationandItsVerificationforAl-2024AluminumAlloy[J].InternationalJournalofNon-linearMechanics, 2013, 51:145-151.

[19]中國國家標準化管理委員會,GB/T15248-2008 金屬材料軸向等幅低循環疲勞試驗方法[S]. 北京: 中國標準出版社, 2008.

(編輯蘇衛國)

A Damage Model for Fatigue-creep Interaction Based on Entropy Increase Theory and Its Experimental Verification

Chen Ling1, 2Zhang Xianming1Liu Fei2Ouyang Ping1Liu Xianbin1

1.Engineering Research Center for Waste Oil Recovery Technology and Equipment of Ministry of Education, Chongqing Technology and Business University, Chongqing, 400067 2.Chongqing University, Chongqing, 400044

Abstract:According to the classical theory of thermodynamics, the fatigue-creep interaction damage of the material might be regarded as the accumulation of the entropy increase. When this accumulation reached to the critical point, the failure occured. From this theory, using the change of the entropy increase to describe the material damage, a damage model for fatigue-creep interaction was developed herein based on CDM and the law of energy conservation. To verify this damage model, the fatigue-creep interaction tests of 1.25Cr0.5Mo steel were conducted with the trapezoidal wave loading under stress control at 540℃ and 520℃. According to the tests, the change of the residual strain, which might reflect the accumulation of the entropy increase of the material, was defined as the damage variable. With this definition, the damage curves of different loading conditions were obtained by the above fatigue-creep interaction damage model. Results show that the damage values measured from experiments are in good agreement with these damage curves, which means that the damage model presented herein may describe the fatigue-creep interaction damage evolution well.

Key words:fatigue-creep; entropy increase; continuum damage mechanics(CDM); damage variable; residual strain

收稿日期：2015-07-02

基金項目：中國博士后科學基金資助項目(2015M582523)；國家自然科學基金資助項目(51375516)；重慶市教委科學技術研究項目(KJ1500624)；教育部平臺科技項目(fykf201502)；重慶工商大學科研啟動經費資助項目(2014-56-10)

中圖分類號：O346.5，TG115.5

DOI：10.3969/j.issn.1004-132X.2016.10.019

作者簡介：陳凌，男，1979年生。重慶工商大學廢油資源化技術與裝備教育部工程研究中心高級工程師,重慶大學機械工程學院博士后研究人員。主要研究方向為金屬材料的疲勞、斷裂、腐蝕及機械結構安全評估。獲中國發明專利10項。發表論文50余篇。張賢明，男，1955年生。重慶工商大學廢油資源化技術與裝備教育部工程研究中心教授。劉飛，男，1948年生。重慶大學機械工程學院教授、博士研究生導師。歐陽平，男，1979年生。重慶工商大學廢油資源化技術與裝備教育部工程研究中心副研究員。劉先斌，男，1961年生。重慶工商大學廢油資源化技術與裝備教育部工程研究中心教授。