汽車租賃調度問題建模分析

邰志艷 張若東 朱浩 鄭斌 彭科

【摘要】 國內汽車租賃市場興起于1990年北京亞運會，直至2000年左右，汽車租賃市場開始在其他城市發展。本文根據已有數據建立了單目標的運輸規劃模型，給出未來四周每天的汽車調度方案，使總的轉運費用最低，為汽車租賃調度提供了新思路。

【關鍵詞】 運輸模型 最小元素法 Microsoft Visual C++6.0

一、問題重述

某城市有一家汽車租賃公司，此公司年初在全市范圍內有379輛可供租賃的汽車，分布于20個代理點中。每個代理點的位置都以地理坐標X和Y的形式給出，單位為千米。試給出未來四周內每天的汽車調度方案，在盡量滿足需求的前提下，使總的轉運費用最低。

二、變量說明

Zm：第m天轉運費用；Cij：i地提供給j地的汽車的轉運費用；

xij：i地提供給j地的汽車；aij：j地所需汽車輛；

bij：i地可提供車輛；Z總總運輸費用。

三、模型的建立與求解

將已知數據放入Microsoft Visual C++ 6.0中進行計算得到不同代理點之間的距離，見下表。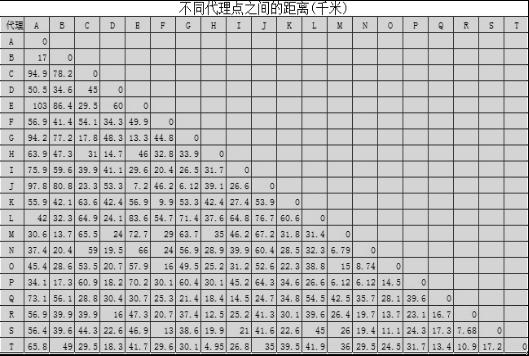

進而計算各代理點之間的轉運成本，第一天為年初各代理點擁有汽車數量，以此為基礎可以算出第二天各代理點之間的供需關系，如下表：

其中正數代表提供汽車，負數代表需求汽車。

建立運輸模型，將提供汽車的代理點視為產地，需求汽車的代理點視為銷地。所以有目標函數：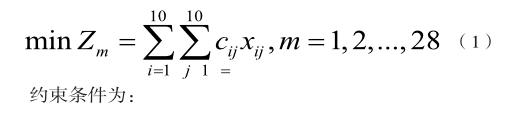

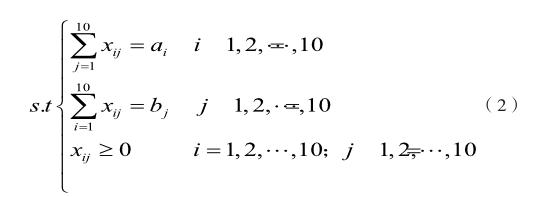
計算得，提供汽車的代理點視為產地，需求汽車的代理點視為銷地，做出下表：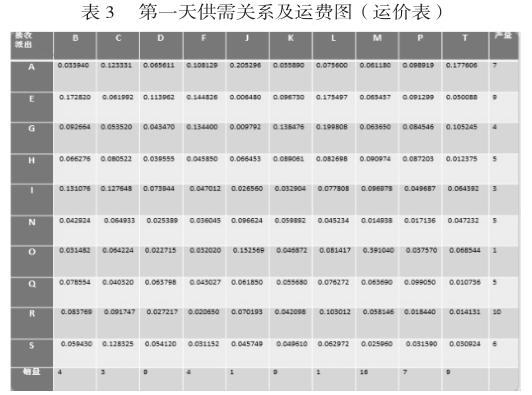

利用Microsoft Visual C++6.0實現最小元素法，得出調度方案為：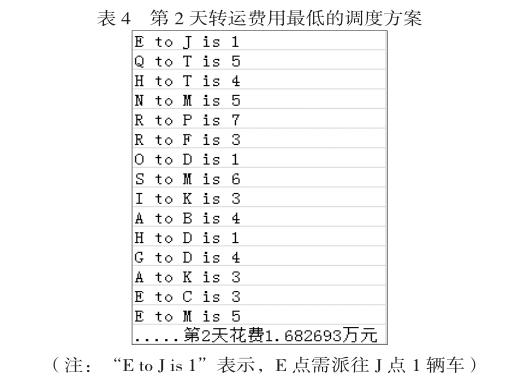

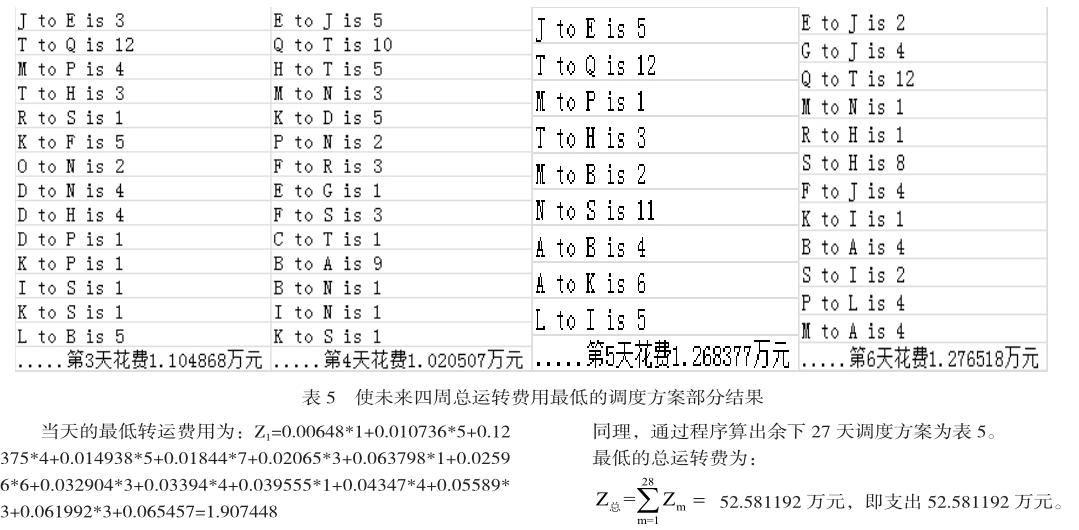
參 考 文 獻

[1]姜啟源、謝金星、葉俊，《數學建模（第四版）》，高等教育出版社，2011.1。

[2]百度百科，最小元素法，http：//baike.baidu.com/link？url=9BqLXt-fOL5ow82yefOPYyNv IKMVdy2N0fGHSS7rQUZxbPj9ABYe7Z1EGxEYDZ0TSpgOLmtNSFPxqTwAQiwdOK

[3] 佟昕、高強，統計學中的數據缺失及解決方法，http：//wenku.baidu.com/view/ ca3f8849e45c3b3567ec8b56.html 2011第二期