根軌跡的中心點研究
2016-05-30 10:55:54董宇
教育教學論壇 2016年13期
董宇


摘要:根軌跡的中心點性質確定了根軌跡中心點的坐標。本文給出了根軌跡中心點性質的新證明方法。首先,證明了當被控對象的傳遞函數為嚴真時,根軌跡存在漸近線;然后,計算了根軌跡漸近線的傾斜角;最后,通過建立漸近線的矢量方程,確定了根軌跡的中心點坐標。與傳統的證明方法相比,本文提出的證明方法具有明確的幾何意義。
關鍵詞:根軌跡;中心點;矢量方程
中圖分類號:G642.4 文獻標志碼:A 文章編號:1674-9324(2016)13-0211-03
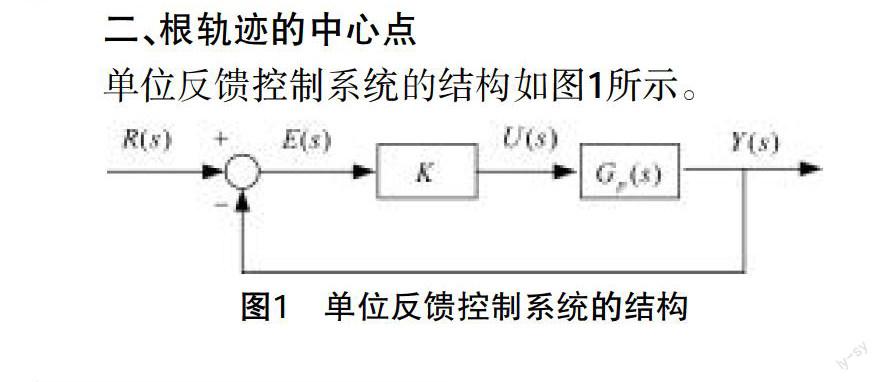
一、引言
根軌跡法是一種基本的控制系統分析設計方法。為了能夠手工繪制根軌跡圖,需要從理論上推測根軌跡在某些位置處的形狀。Evans提出了基本的根軌跡性質。[1]此外,許多學者對根軌跡的性質進行了深入的研究。文獻[2]計算了根軌跡分離點處的出射角和入射角。文獻[3]計算了當原點作為根軌跡的多重零點和多重極點時,相應的入射角和出射角。文獻[4]計算了實數零點和實數極點處根軌跡的入射角和出射角。文獻[5]計算了當傳遞函數為假有理分式時,根軌跡漸近線的傾斜角。文獻[6]計算了多重起始點和終止點處根軌跡的出射角和入射角。而文獻[7]使用矢量分析方法,對上述根軌跡性質進行了重新計算,得到了更為簡潔的計算結果。文獻[8]給出了根軌跡存在分離點的代數形式的充分必要條件。
教科書中闡述的關于根軌跡中心點的性質用于確定根軌跡中心點的坐標。但教科書中對根軌跡中心點性質的證明是形式化的,未能對其中的機理進行深入的分析。本文提出了一種關于根軌跡中心點性質的新證明方法,該證明方法具有明確的幾何意義。首先,證明了當被控對象傳遞函數為嚴真時,根軌跡在無窮遠點處存在漸近線;然后計算了漸近線的傾斜角;最后,通過建立漸近線的矢量方程,確定了根軌跡中心點的坐標。

