一種用于多點定位系統的實時高精度位置解算方法
馬廣亮 劉曉偉


摘 要:多點定位系統是國際民航組織著力推廣的新一代監視設備,工程應用研究正不斷完善,而如何實時地提取目標的精確位置一直是該系統不斷深入研究的難題。該文利用Chan算法、Taylor級數展開法、自適應Kalman濾波算法聯合進行位置解算,確保多點定位系統中心處理單元的解算速度和解算精度,從而實時獲取高精度的目標位置信息,使其能進一步滿足國際民航監視精度要求。
關鍵詞:多點定位 chan算法 Taylor級數Kalman濾波
中圖分類號:V24 文獻標識碼:A 文章編號:1672-3791(2016)07(b)-0121-04
多點定位系統[1]是國際民航推廣的五大監視技術[2]之一。多點定位系統能夠對裝備了普通A/C/S模式應答機的飛機實時高精度可靠監視,但這種實時高精度可靠監視是基于應答信號到達時間(TOA)的高精度測量以及目標位置的實時、精確解算。在工程應用中,尋找一種實時、高效的目標位置解算算法是多點定位系統問世以來深入研究的課題之一。
傳統的多點定位方法主要采用的是Chan算法[3]、Taylor級數展開法[4]、Friedlander算法[5]、Fang算法[6]等為代表的視距定位計算方法。Chan算法計算量小,無需迭代運算,但在非視距環境下定位精度較差;Taylor級數展開法則需要一個迭代初值進行迭代運算,才能在短時間內解算得到精確目標位置;Friedlander算法對遠端單元的數量有較大依賴型,當數量減少時,定位精度明顯降低;Fang算法等為代表的視距算法不符合多點定位系統實際工程超視距的需要。
總之,上述任何一種位置解算方法都或多或少存在缺陷,不能在成本控制、實時性和定位精度3者間取得最佳平衡。因此,必須尋找一種實時、高精度目標位置解算方法,以滿足工程應用中的需求。
1 原理
該文利用算法之間的不同特性并基于所到達時間差(TDOA)對目標位置進行聯合運算。聯合定位算法的流程框圖如圖1所示。
針對上圖中每個步驟的實現原理,后續內容將作詳細的闡述。
首先,對多組數據進行匹配,每隔△t1時間,以主單元接收到信息的時間和內容為基準,與其前后△t2時間長度內其他副單元接收信息內容進行比對。若有相同信息內容的目標,則作為有效信息用于后續運算,否則,每條信息經過△t3時間后被濾除。其中△t1、△t2、△t3三個時間根據各接收單元實際分布情況進行確定;目前該算法中△t1=1 s、△t2=300 ms、△t3=3 s。
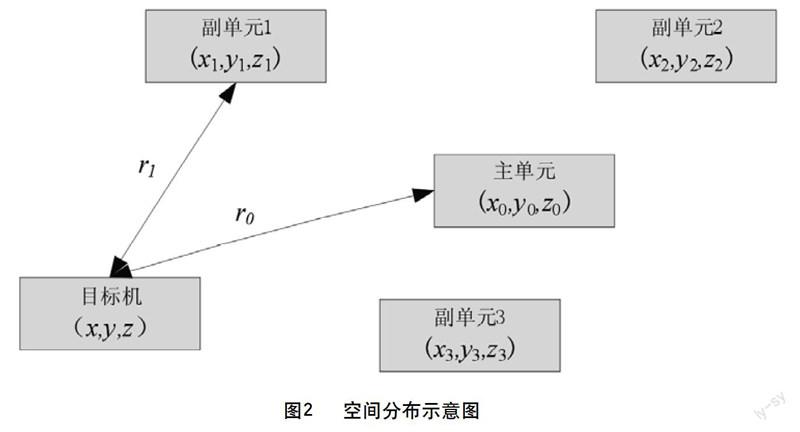
其次,利用上一步所獲取的有效信息進行運算,如圖2所示。
圖中,各遠端接收單元的空間位置為(xi,yi,zi),主單元為(x0,y0,z0)。(x,y,z)為目標的位置坐標,目標與第i個副單元的距離為ri,△ri代表目標到主單元與第i個副單元之間的距離差。
最后,由于應答數據或廣播數據的每種模式速率不同以及TOA的測量誤差,導致上述算法運算后目標點跡分布不均勻,通過自適應Kalman濾波算法后可以形成分布均勻且穩定的初始航跡。同時,該種方法能更好的解決機動目標的定位。
經典卡爾曼濾波[7]:假定A和B為系統參數,H為測量系統的參數,表示利用上一狀態預測的當前狀態,X 表示上一狀態最優結果,U 為系統控制量,W 為系統過程噪聲,的協方差矩陣,A′為A的轉置矩陣,Q為W 的協方差矩陣,Z (k)為當前狀態測量值,Kg為卡爾曼增益,R為U(k)協方差,I 為單位矩陣。則它可由下面5個公式表達:
對于非機動目標來說,其運動數學模型可以精確描述,經典Kalman濾波可以很好地完成對目標的估計和預測。但對于機動目標的定位,則需要對卡爾曼濾波進行適當改進。該算法中采用一種自適應卡爾曼濾波算法,將機動加速度看成虛擬誤差,假定目標仍做勻速運動。則經典的卡爾曼濾波公式可改寫為:
上式中:V(k)為未知的機動加速度,Qw+v為[W(k)+V(k)]的協方差。對于機動目標應強調新近機動加速度數據的作用,對于陳舊的數據應漸漸遺忘,這里采用漸消記憶指數加權方法來實現。即在對加速度假設的噪聲進行統計估值時,式中每項乘以不同的加權系數,按指數加權法,選取加權系數βi 使之滿足:
上式中:b成為遺忘因子,用(1-dk-1)/(k-1)作為權系數,得到指數加權漸消記憶的時變噪聲統計估值器。
2 工程仿真分析
為了驗證該算法的有效性,多點定位系統采用了5個遠端接收單元。在向后臺傳輸數據時,利用150 MHz的無線Wifi組成局域網,后臺通過該局域網實時接收各個遠端單元發送目標信息,并通過聯合算法對目標位置進行運算。
由于聯合解算方法采用chan算法獲取目標的初始位置,其運算收斂的速度比單獨采用Kalman濾波算法收斂得更快,通常會在3~5次迭代過程收斂,這樣,在目標容量大的情況下,能夠大量地減少運算復雜度,降低硬件運行環境配置,減少工程的實施成本;該聯合算法通過迭代獲取的目標位置更趨向目標的真實位置,在相同TOA精度情況下,目標解算位置精度更高;該聯合解算方法采用自適應Kalman濾波進行航跡處理,對于機動能力較高的飛行目標,能夠產生連續穩定的初始航跡,較好地適應高機動目標的監視。
3 結論
綜上所述,采用該文所設計的目標位置聯合解算方法,有如下優點。
(1)算法結構簡單,計算復雜度低,運算量小,對硬件運行環境要求不高,有效降低多點定位系統工程應用成本。
(2)通過Chan算法、Taylor級數展開法和Kalman濾波算法聯合解算,多點定位系統能夠在實時性和定位精度上達到最佳平衡。
(3)工程應用推廣性強,在對隱身飛機、手機定位跟蹤等眾多軍、民用領域有著廣泛的應用前景。
參考文獻
[1] W.H.L.Neven.T.J.Quilter,R.Weedon,R.A. Hogendoorn[J].Wide Area Multilateration Report on EATMP TRS 131/04 Version 1.1.2005(8):9-10.
[2] ICA Organization.Aeronautical Surveillance Manua[M].International Civil Aviation Organization,2010.
[3] Y.T.Chan,K.C.Ho.A Simple and Efficient Estimator for Hyperbolic Location[J].IEEE Transactions on Signal Processing,1994,42(8):1905-1915.
[4] WHFoy.Position Location Solutions by Taylor Series Estimation[J].IEEE Transactions on Aerospace and Electronic Systems,1976,AES-12(2):187-194.
[5] B Friedlander.A passive localization algorithm and its accuracy analysis[J].IEEE Journal of Oceanic Engineering, 1987,12(1):234-245.
[6] BT Fang.Simple solutions for hyperbolic and related position fixes[J].IEEE.Trans.Aerosp.Electron Syst, 1990,26(5):748-753.
[7] B Rudolf.Emil Kalman.A New Approach to Linear Filtering and Prediction[J].ProblemTransactions of the ASME-Journal of Basic Engineering,1960(82):34-45.

