基于H∞方法的控制系統作動器最優控制仿真研究

趙一瑾

(北京航空航天大學 無人駕駛飛行器設計研究所, 北京 100191)

?

基于H∞方法的控制系統作動器最優控制仿真研究

趙一瑾

(北京航空航天大學 無人駕駛飛行器設計研究所, 北京 100191)

摘要:在設計控制系統模型時,首先引入了有限差分法(FDM)離散化后的波動方程,然后基于H∞最優控制原理,檢查閉環控制系統的穩定性和可探測性,對控制系統傳感器和作動器的位置進行優化配置。通過計算閉環反饋系統的范數,最終得到了控制系統的最優控制算法。仿真結果表明,利用波動方程來優化控制系統傳感器和作動器位置的算法是可行的,可廣泛應用于飛控系統的設計中。

關鍵詞:傳感器和作動器; 有限差分法; H∞最優控制

0引言

現代控制領域中最重要的內容之一就是尋找傳感器和作動器的最優位置,以獲得更好的控制結果。傳感器的不當放置,可能會導致其精度降低,影響控制效果。

自20世紀七八十年代起,人們開始了對控制系統和顯示系統中傳感器和作動器位置的研究。1973年,文獻[1]提出通過檢測系統的可觀測性確定傳感器的優化配置。之后,研究者們開始關注于在傳感器位置最優問題上如何減少估計誤差[2]。文獻[3]通過對線性偏微分方程(PDE)模型的控制器進行可控性測量,來得到最佳的作動器的位置。后來文獻[4]將遺傳算法引入到優化控制器增益和作動器位置研究中。對于非線性控制系統,Lou等[5]嘗試用K-S方程的高階離散來計算。盡管這些前期的方法和研究取得了一定的進展,但在魯棒性方面均存在不足。隨著現代控制理論的發展,魯棒控制系統被引入到這一問題中來。文獻[6]利用線性Ginzburg-Landau模型來設計H2控制器,但相較于H∞最優控制理論,H2控制理論存在更多的局限性。

考慮到實際工程應用中飛機作為一個彈性體,在設計控制器時必須考慮柔性結構的因素，本文將現代H∞魯棒控制理論與柔性結構的波動方程相結合,來解決作動器和傳感器位置最優的問題。利用有限差分法(FDM)來離散化波動方程,它的線性偏微分方程可以通過物理學原理推導得出[7]。H∞最優控制原理被應用于設計控制系統,它擁有傳統控制方法的所有優點，并且很好地平衡了控制器的表現和魯棒性[8]。H∞最優控制的目標是減小閉環系統從外界輸入到誤差信號輸出的范數γ∞。

1被控系統的離散化

1.1偏微分方程

由于一維波動方程沒有阻尼項,其所有特征值均在虛軸上即實數部分為零,整個開環系統處于臨界穩定狀態。為了使系統穩定,須引入阻尼項來確保所有矩陣的特征值都處于左半平面上。一維有阻尼項的波動方程的偏微分方程為[7,9]:

(1)

式中:x為波的振幅;s為位置矢量;c為波的傳播速度;λ為阻尼系數。假設在機翼的底端有脈沖輸入信號,則初始條件(IC)和邊界條件(BC)分別為:

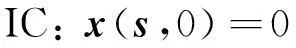
(2)

(3)

1.2有限差分方法

用有限差分法對偏微分方程進行離散化[10],下面是兩種離散方法。

1.2.1全離散有限元差分法

離散化整個系統,將其分為N個點,時間T分為M個節點,所以空間和時間上的步長可分別表示為Δs=L/(N-1),Δt=T/(M-1)。一階差分用向前差分法,二階用中心差分法,可離散化一維有阻尼項的波動方程為:

(4)

式中:i為空間網格;j為時間網格。用p=c2Δt2/Δs2替代,重新整理式(4)可得:

(5)

寫成矩陣格式為:

(6)

1.2.2半離散有限元差分法

半離散法僅在空間上離散而不在時間上進行離散,即Δs=L/(N-1)。離散時對于各節點處n=0,1,…,N-1,可使用二階向前差分、二階向后差分以及二階中心差分法,其表達式分別如式(7)～式(9)所示:

(7)

(8)

(9)

2H∞最優控制系統

2.1H∞最優控制原理

一個典型的H∞反饋控制系統的結構框圖如圖1所示。

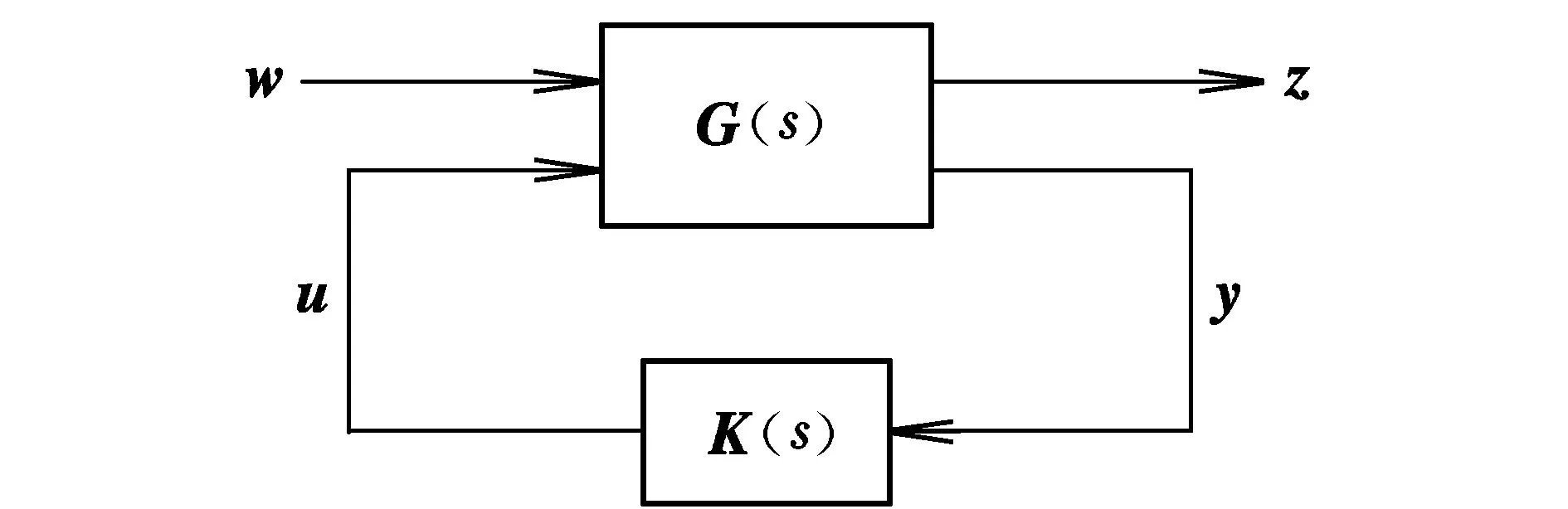
圖1　H∞反饋控制系統結構框圖Fig.1　Structure of H∞ feedback control system

圖1的反饋控制系統可以看作一個下線性分式變換(LFT)。圖中：G(s)為被控對象;K(s)為控制器[11-12];u為控制輸入;y為測量輸出;w為所有外部輸入,包括干擾或噪聲;z為系統的輸出即錯誤信號。該系統可以表示為:

(10)

通過一系列推導可得系統從外部輸入w到誤差信號z的傳遞函數為[13]:

(11)

此系統的狀態空間表示為:

(12)

所以傳遞函數可以表示為:

(13)

系統的H∞范數γ代表系統最壞的情況或可能出現的最大增益。定義為[11-13]:

(14)

2.2H∞閉環控制器的設計

用狀態空間描述開環系統[14]:

(15)

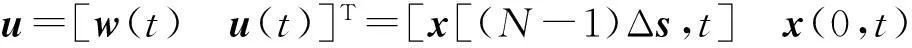
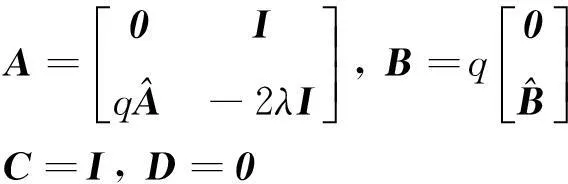
其中:

利用H∞最優控制理論設計一個閉環控制系統,寫成式(12)的形式。

2.3位置最優設計

2.3.1傳感器位置最優

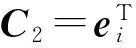
2.3.2作動器位置最優

3仿真結果及分析

假設:波的傳播速度c=1 m/s;介質長度L=10 m;分割節點數N=15;總測量時間T=10 s;時間節點數M=100;外界脈沖輸入的邊界條件uL=10 mm;阻尼項的阻尼系數λ=1。

3.1H∞閉環控制系統

閉環系統的H∞范數γclosed是用來測量H∞最優控制系統的控制效果的一項非常重要的指標。

對于不同的r,閉環系統的脈沖響應分別如圖2所示。當r=0時,為了平衡位于介質末端的正向波動,靠近介質起始端的節點處的響應是負向的。隨著系數r的不斷增大,這個響應在不斷減小,當r趨近于正無窮大時,對比開環和閉環系統的范數可知,γclosed會趨近于γopen,此時意味著控制器對系統的影響小到可以忽略不計。

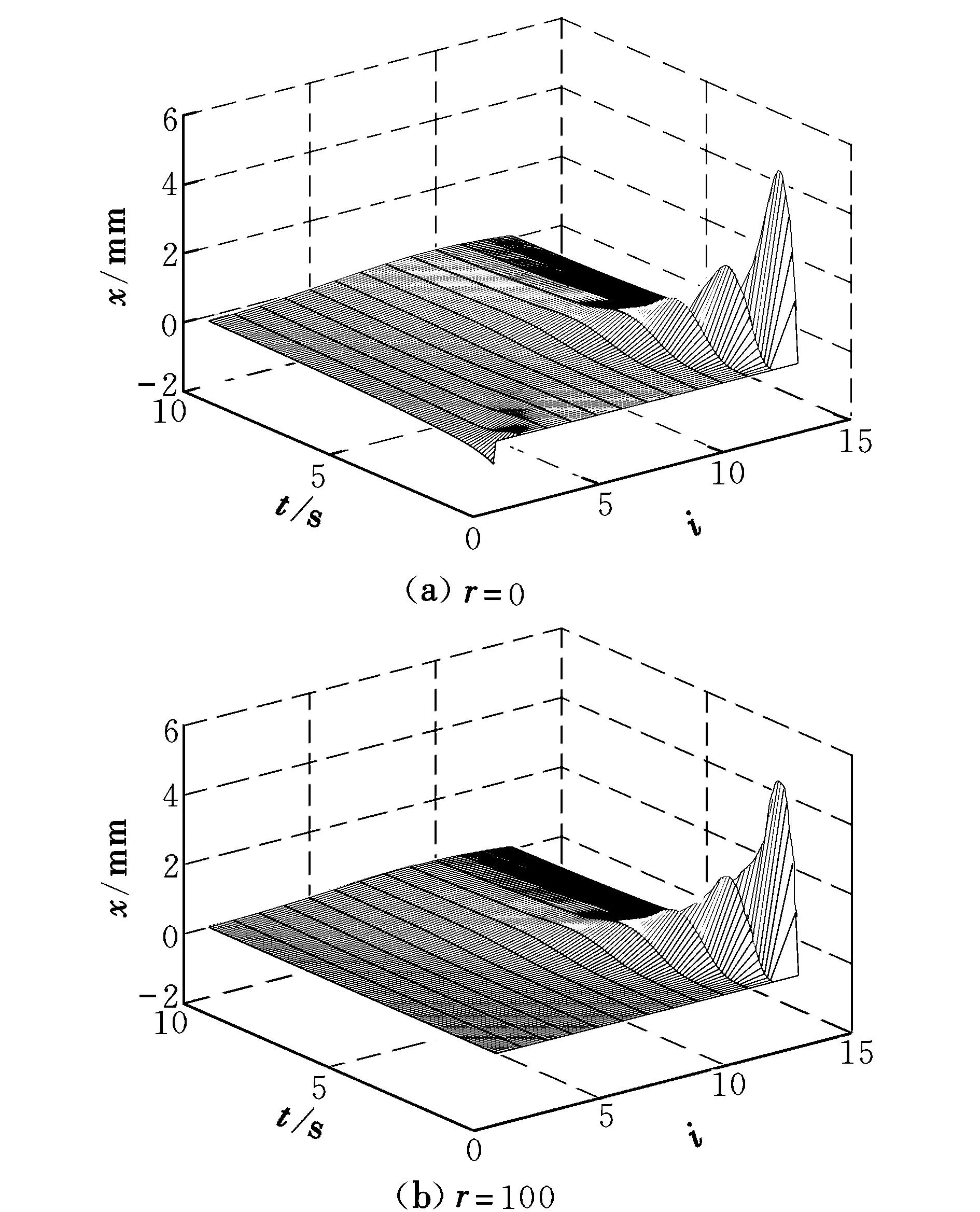
圖2　含阻尼項波動方程的脈沖響應Fig.2　Impulse responses of closed-loop system for wave equation with damping term

通過對比不同r情況下閉環系統和開環系統的H∞范數,可以得出如下結論:當r不斷增大,會使得控制輸入u變小,從而導致控制器在閉環系統中所起到的作用非常小。當r足夠大時,閉環系統的H∞范數會無限趨近于開環系統的H∞范數,這說明閉環系統的控制效果與開環系統一樣變得非常差。

3.2傳感器位置最優

根據第2.3.1節關于傳感器位置最優的研究,移動傳感器測量輸出的位置,則系統的脈沖響應如圖3所示。當測量輸入向位于底端的外界輸入移動時,位于遠離w的作動器反應越來越迅速,這表明了控制器的效果不斷提高。

圖3　移動傳感器位置時波動方程的脈沖響應Fig.3　Impulse responses of closed-loop system with the position of sensor being moved

此時若將u固定在其他節點處,移動測量輸出y的位置時,會出現系統不可探測的情況,增加傳感器的個數可以使系統重新變為可探測的。

3.3作動器位置最優

按照本文第2.3.2節所述的過程進行作動器位置最優的研究,移動作動器即控制輸入的位置。表1為作動器位置不同時閉環系統的H∞范數。其中，γ1為u=x(0,t)時γclosed的最小值;γ2為u=x(Δs,t)時γclosed的最小值。對比可知,將作動器放在起始端,會得到更好的控制效果。繼續移動作動器的位置,可能會出現系統不穩定的情況,這意味著僅用一個作動器無法使系統穩定,此時可以通過增加作動器的個數來解決這一問題。

在研究一個傳感器作動器位置最優問題時,會出現系統不穩定或不可探測的情況,此時可以通過增加傳感器或作動器的數量來使系統重新恢復到穩定、可探測的狀態。

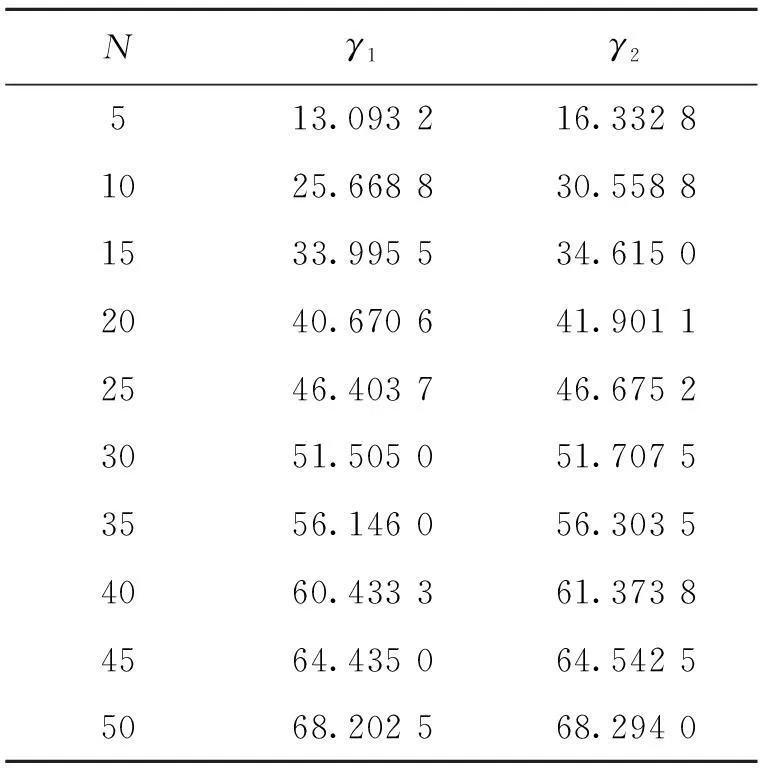
表1　作動器位置不同時閉環系統的H∞范數

4結束語

基于H∞最優控制原理,利用波動方程來優化控制系統傳感器和作動器位置的算法是可行的,可以將傳感器和作動器的位置最優問題轉化為控制系統的優化問題。可以通過測量控制系統的H∞范數判斷閉環系統的控制效果,給復雜的位置最優問題一個固定的檢測標準。在滿足系統穩定性和可探測性的前提下,可以進一步研究多個傳感器及作動器位置最優的問題。

參考文獻：

[1]Yu T K,Seinfeld J H.Observability and optimal measurement location in linear distributed parameter systems[J].International Journal of Control,1973,18(4):787-789.

[2]Kumar S,Seinfeld J H.Optimal location of measurements for distributed parameter estimation[J].IEEE Transactions on Automatic Control,1978,23(4):690-698.

[3]Arbel A.Controllability measures and actuator placement in oscillatory systems[J].International Journal of Control,1981,33(3):565-574.

[4]Rao S S,Pan T S,Venkayya V B.Optimal placement of actuators in actively controlled structures using genetic algorithms[J].American Institute of Aeronautics and Astronautics Journal,1991,29(6):942-943.

[5]Lou Yiming,Christofides P D.Optimal actuator/sensor placement for nonlinear control of the Kuramoto-Sivashinsky equation[J].IEEE Transactions on Control Systems Technology,2003,11(5):737-745.

[6]Chen K K,Rowley C W.H2optimal actuator and sensor placement in the linearised complex Ginzburg-Landau system[J].Journal of Fluid Mechanics,2011,18(6):241-260.

[7]Alterman Z,Karal F C.Propagation of elastic waves in layered media by finite-difference methods[J].Bulletin of the Seismological Society of America,1968,58(1):367-398.

[8]Barmish B R.New tools for robustness of linear systems[M].New York:Macmillan Publishing Company,1992.

[9]Carcione J M.The wave equation in generalized coordinates[J].Geophysics,1994,59(3):1911-1919.

[10]Morton K W,Mayers D F.Numerical solution of partial differential equation[M].Cambridge:Cambridge University Press,1994.

[11]Ackermann J,Bartlett A,Kaesbauer D,et al.Robust control: systems with uncertain physical parameters[M].London:Springer,1993.

[12]Anderson B D O,Moore J B.Optimal control:linear quadratic methods[M].New Jersey:Prentice Hall,Englewood Cliffs,1990.

[13]Skogestad S,Postlethwaite I.Multivariable feedback control:analysis and design[M].second edition.Chichester:Wiley,Chichester,2005.

[14]Katsuhiko Ogata.Modern control engineering[M].fifth edition.New Jersey:Prentice Hall,2009.

(編輯：方春玲)

Simulation of optimal control actuators for a control system based onH∞theory

ZHAO Yi-jin

(Unmanned Aircraft Design and Research Institute, BUAA, Beijing 100191, China)

Abstract:This paper proposes a new way to address this issue, in which wave equation discretized by the finite differential method (FDM) was used to describe the input/output propagation mode for control systems. By utilizing a robust controller design to the models, the complicated optimal actuator and sensor placement problem can be transformed to a judgement on specific characteristics. Check the stability and detectability of the closed-loop control system based on the H∞optimal control principles. The simulation results show that the process of optimizing the placement of sensors and actuators for control and monitoring system could also serve as a natural extension to other structures.

Key words:sensor and actuator; finite differential method (FDM); H∞optimal control

中圖分類號：V249.1

文獻標識碼：A

文章編號：1002-0853(2016)02-0028-04

作者簡介:趙一瑾(1993-)，女，陜西西安人，碩士，研究方向為飛行力學與控制工程。

收稿日期:2015-11-08;

修訂日期:2016-01-19; 網絡出版時間:2016-03-15 14:29