基于動態逆-滑模的高速飛行器控制器設計

李飛, 李新國

(西北工業大學 航天飛行動力學技術國家重點實驗室, 陜西 西安 710072)

?

基于動態逆-滑模的高速飛行器控制器設計

李飛, 李新國

(西北工業大學 航天飛行動力學技術國家重點實驗室, 陜西 西安 710072)

摘要:吸氣式高超聲速飛行器巡航狀態下飛行環境復雜,建模時存在非線性以及參數攝動。基于小擾動假設的傳統經典控制理論難以適應當前任務對魯棒性的要求,對此提出了一種非線性動態逆-滑模控制律改進方法。通過對吸氣式高超聲速飛行器模型精確反饋線性化得到解耦形式的線性方程,為速度和高度設計出動態逆控制律來抵消非線性特性,在動態逆的基礎上采用滑模變結構來補償參數攝動帶來的誤差。仿真結果表明，所設計的控制方法具有良好的動態性能及魯棒性。

關鍵詞:非線性動態逆; 滑動模態變結構控制系統; 反饋線性化

0引言

目前,隨著航天技術的不斷創新與發展,高超聲速飛行器成為各軍事強國爭相研究的焦點。高超聲速飛行器飛行環境復雜,加之飛行器對飛行條件變化敏感,如果控制器設計不合理就會導致飛行過程發散,無法達到既定任務要求,因此有必要設計跟蹤性能好、魯棒性強的飛行控制系統。

傳統的飛行器控制系統是建立在小擾動假設下的,難以適用于高度非線性以及具有參數攝動的高超聲速飛行器飛行控制系統設計中。目前國內外學者的研究主要集中在非線性控制以及魯棒控制方面。文獻[1]采用自適應反步控制器對高超聲速飛行器存在參數不確定的情況進行控制;文獻[2]通過采用μ分析方法設計了高超聲速飛行器魯棒控制系統;文獻[3]對非線性控制中神經網絡法以及魯棒自適應方法做了深入研究;文獻[4]將高超聲速飛行器耦合系統表示為具有非匹配不確定性關聯大系統形式,利用Lyapunov穩定理論及Riccati方程設計滑模變結構控制律。

本文針對高超聲速飛行器耦合控制以及參數攝動問題,提出了動態逆-滑模控制方法。采用動態逆將非線性形式轉化為線性形式,線性化后的系統能夠精確保留原系統的信息,在此基礎上采用滑模控制抵消參數攝動帶來的誤差,充分結合了兩種方法的優勢。因此,較線性飛行控制系統而言，動態逆-滑模控制結構具有較強的控制精度及魯棒性。最后在Matlab/Simulink中進行了數字仿真,針對某吸氣式高超聲速飛行器在巡航狀態下對速度指令、高度指令的跟蹤驗證了控制器的性能。

1吸氣式高超聲速飛行器建模

1.1吸氣式高超聲速飛行器數學模型

假設地球為均勻圓球體,不考慮地球自轉效應,且飛行器側滑角為零,只考慮飛行器縱向運動。將發動機節流閥調節值與舵面偏轉角作為控制量,則吸氣式高超聲速飛行器飛行動力學方程為[5]:

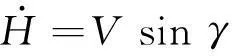
(1)

(2)

(3)

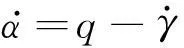
(4)

(5)

(6)

(7)

(8)

(9)

(0.001 2Ma2-0.054Ma+1)

(10)

其中,由迎角產生的力矩系數CM(α)、由俯仰角速度產生的力矩系數CM(q)和由舵偏角產生的力矩系數CM(δe)可由飛行器巡航狀態下的經驗公式得到:

CM(α)=10-4(0.06-e-Ma/3)×

(-6 565α2+6 875α+1)

(11)

(6.83α2+0.303α-0.23)

(12)

CM(δe)=0.029 2(δe-α)

(13)

發動機推力計算公式為:

T=0.5ρV2SCT

(14)

推力系數采用分段形式計算:

(15)

發動機動態方程采用二階系統模型:

(16)

式中:δT為發動機節流閥調節值;δTcom為油門開度;在此可取k1=k2=0,k3=1。

1.2非線性動態逆原理

非線性動態逆通過輸出或狀態反饋,將非線性系統(全部或部分)轉換為解耦規范系統——偽線性系統,采用線性系統設計理論設計控制系統達到設計要求。

考慮多輸入-多輸出系統(MIMO)為:

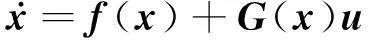
(17)

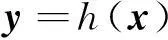
(18)

式中:G(x)=[g1(x),g2(x),…，gm(x)];f和gi(i=1,2,…,m)為光滑向量場;h為光滑函數。輸出方程的李導數為:

(19)

(20)

因此輸出方程可表示為:

(21)

引入反饋控制律:

u=-[G*(x)]-1f*(x)+[G*(x)]-1υ

(22)

式中:G*(x)為非奇異矩陣,加入積分環節來產生有定義的相對階,本文在發動機節流閥控制中加入了積分環節確保相對階完整定義;υ為新的輸入控制量,因此可以設計υ得到非線性控制律u。將式(22)代入式(17)中得到解耦輸出方程:

(23)

2輸入輸出線性化

高超聲速飛行器在巡航狀態下接收到控制指令后,發動機推力以及升降舵會作出響應,因此控制輸入為發動機節流閥調節值δT和升降舵偏轉角δe。為了簡化推導過程,令:

(24)

分別對輸出動態方程式(21)中的V微分3次,h微分4次，可得到關于控制量的表達式,因此輸出方程表示為:

(25)

其中:

(26)

(27)

(28)

(29)

(30)

(31)

向量ω1,π1以及矩陣Ω2,Π2定義見文獻[5]。

按式(22)設計控制律時,G*應為非奇異矩陣,即:

(32)

由式(32)可知,當航跡角γ≠90°且 (T+Lαcosα

+Dαsinα)≠0時,G*為非奇異的。

定義非線性坐標轉換:

(33)

(34)

因此,解耦形式為:

(35)

(36)

其中:

(37)

(38)

3滑動模態變結構控制律設計

滑模變結構控制律設計的主要任務是設計適當的切換函數和變結構控制律,使系統狀態軌跡能夠在有限時間內到達所設計的滑模面上,并以適當的速度沿著它滑向平衡點。

針對系統式(35),引入狀態反饋型滑模控制面s(x)=C1x(t),則簡約型變結構控制系統為:

(39)

根據滑動模態定義,一旦系統狀態x進入滑動模態域將只能沿其運動,且滑動運動滿足:

(40)

將系統狀態方程式(39)中第1式代入式(40)中,可得:

C1A1x+C1b1u=0

(41)

若C1b1非奇異,由上式可解出滿足式(40)的等效控制,則在等效控制ueq的作用下,系統將沿著滑動模態運動。

(42)

在本文中為了消除抖振,引入飽和函數M1(s),則變結構控制律υ1的形式如下:

(43)

同理,可求得變結構控制律υ2的形式如下:

(44)

根據任務要求分別將滑動模態運動極點配置在{-0.5,-1+i,-1-i},{-0.25,-0.5,-1+i,-1-i}。 則式(43)、式(44)中滑動模態參數矩陣C1,C2以及飽和函數M1(s),M2(s)分別為:

(45)

C2=[0.251.753.632.751]

(46)

(47)

(48)

圖1　動態逆-滑模控制結構圖Fig.1　Dynamic inversion-sliding mode controller

4仿真分析

以某型吸氣式高超聲速飛行器為例,在Matlab/Simulink下進行仿真試驗,驗證所設計的動態逆-滑模控制結構的控制性能。初始仿真條件為:V=4 590 m/s,H=33 km,S=335 m2,α0=1.81°,分別在有、無初始擾動的情況下進行仿真分析。其中,加入初始擾動參數如表1所示。

采用第3節所設計的動態逆-滑模控制律,在巡航狀態下給定階躍響應:ΔV=100 m/s,ΔH=500 m,分別在有、無初始擾動的情況下進行對比,仿真結果如圖2所示。

表1　擾動參數邊界

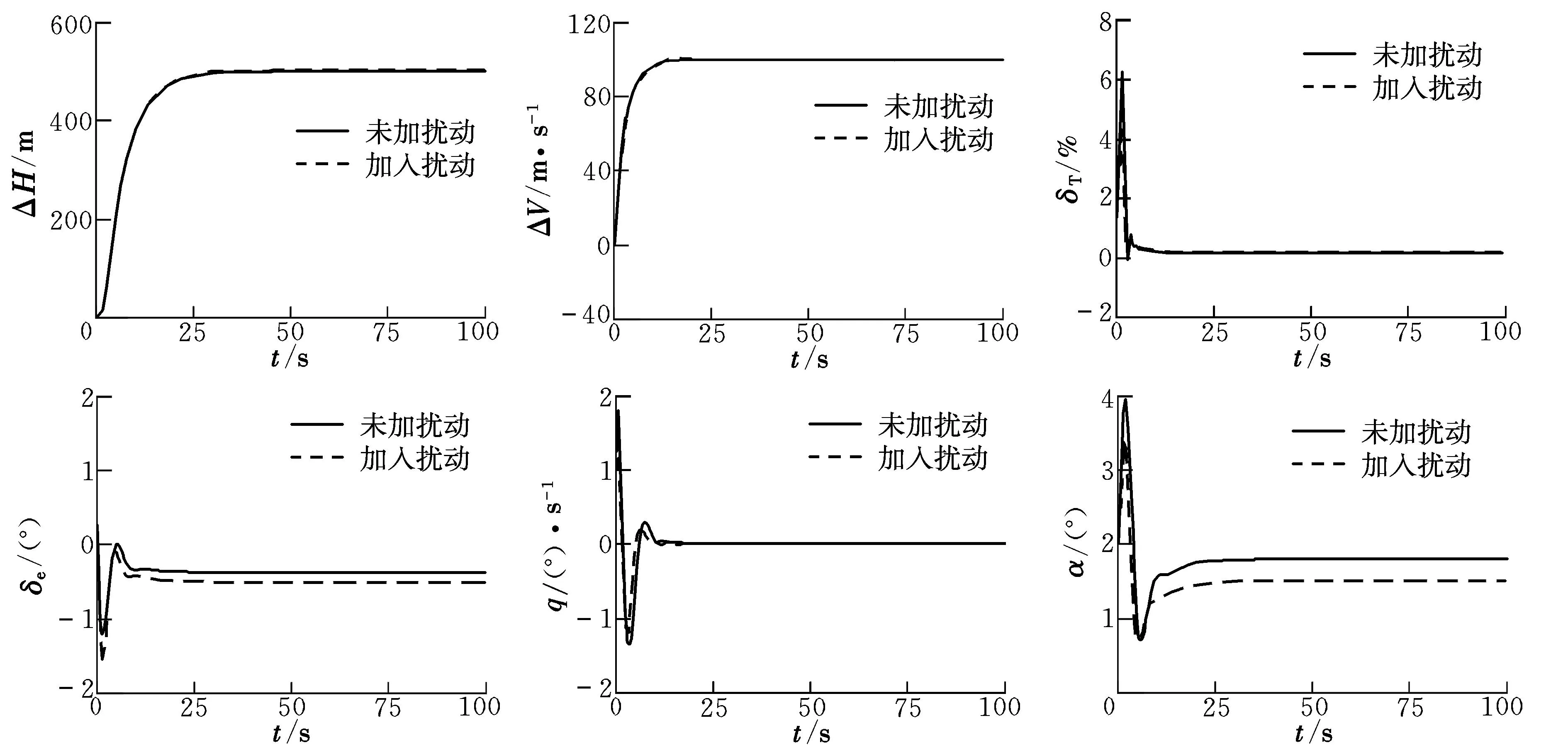
圖2　仿真曲線Fig.2　Simulation curves

由圖可知,所設計的動態逆-滑模控制律對于速度指令以及高度指令能夠在較短時間內達到期望值并保持穩定,且當系統加入過程擾動時跟蹤穩態誤差小,魯棒性強。發動機節流閥開度和舵面偏轉角曲線變化平緩,但由于滑模變結構控制的固有特點導致存在一定的抖振。圖中俯仰角速度迅速收斂為零,迎角曲線迅速收斂為小值,便于維持巡航狀態。

在其他狀態下,所設計的動態逆-滑模控制器響應曲線與前文所述相似,均能使系統具有良好的跟蹤性能及魯棒性,由于篇幅限制,在此就不一一列舉。因此,所設計的動態逆-滑模變結構控制器能夠使飛行器在巡航狀態下抵御由于參數攝動對于系統的影響,具有良好的動態特性和魯棒性。

5結束語

本文針對高超聲速飛行器模型的特點,采用動態逆理論將高度非線性的高超聲速飛行器縱向運動模型解耦,利用滑模控制律對參數攝動不敏感的特點,結合兩者優勢設計出了動態逆-滑模控制結構。通過仿真分析可知,此控制系統對某吸氣式高超聲速飛行器的控制指令能夠做出快速響應,具有良好的跟蹤性能且穩定性好、魯棒性強,為工程應用提供了一種可行方案。

參考文獻：

[1]朱艷明.高超聲速飛行器的非線性控制[D].沈陽:東北大學,2009.

[2]尉建利,于云峰,閆杰.高超聲速飛行器魯棒控制方法研究[J].宇航學報,2008,29(5):1526-1530.

[3]Wu S F,Engelen C J H,Chu Q P.Fuzzy logic based attitude control of the spacecraft X-38 along a nominal re-entry trajectory[J].Control Engineering Practice,2001,9(7):699-707.

[4]周鳳岐,王延,周軍,等.高超聲速飛行器耦合系統變結構控制設計[J].宇航學報,2011,32(1):66-71.

[5]Wang Q,Stengel R F.Robust nonlinear control of a hypersonic aircraft[J].Journal of Guidance,Control,and Dynamics,2000,23(4):577-585.

(編輯：方春玲)

Dynamic inversion-sliding mode for breathing hypersonic vehicle controller design

LI Fei, LI Xin-guo

(National Key Laboratory of Aerospace Flight Dynamics, NWPU, Xi’an 710072, China)

Abstract:Air-breathing hypersonic vehicle cruising flight environment is complex, non-linearity and parameter perturbation exists in modeling. Based on the assumption that it is difficult for small disturbance traditional classical control theory to adapt to the current task robustness requirements, this paper presents a nonlinear dynamic inversion-sliding mode control law improvement. Through the air-breathing hypersonic vehicle model to get precise feedback linearization decoupled linear equations, the dynamic inverse control law is designed for the speed and height to offset the non-linear characteristics. On the basis of dynamic inversion, the sliding mode variable structure is adopted to compensate parameter error caused by perturbation. The simulation results show that the control method is designed with good dynamic performance and robustness.

Key words:nonlinear dynamic inversion; sliding mode variable structure control system; feedback linearization

中圖分類號：V448.2

文獻標識碼：A

文章編號：1002-0853(2016)02-0064-04

作者簡介:李飛 (1990-)，男，河北唐山人，碩士研究生，研究方向為飛行器制導與控制；李新國(1966-)，男，湖南常德人，教授，博士生導師，研究方向為飛行器系統工程與仿真、空天飛行系統與技術。

收稿日期:2015-07-14;

修訂日期:2015-11-03; 網絡出版時間:2016-01-10 14:13