基于直覺模糊的杭州宋城主題公園旅游收入時序預(yù)測的新方法

徐萍麗 張婷婷 張鯤 王鴻緒

摘 要：時序預(yù)測所研究的應(yīng)用問題很廣泛，針對杭州宋城主題公園旅游收入問題，基于直覺模糊時間序列預(yù)測模型進行算法改進與研究，以已知年數(shù)據(jù)進行模擬預(yù)測，得出較小的誤差率，在已有方法的基礎(chǔ)上，構(gòu)造新公式與新算法，從而推論對未知年份預(yù)測方法的可行性，以提高預(yù)測精度。

關(guān)鍵詞：模時間序列預(yù)測；百分比；百分比的分段；逆模糊數(shù)

中圖分類號：F590 文獻標(biāo)志碼：A 文章編號：1673-291X（2016）07-0159-06

引言

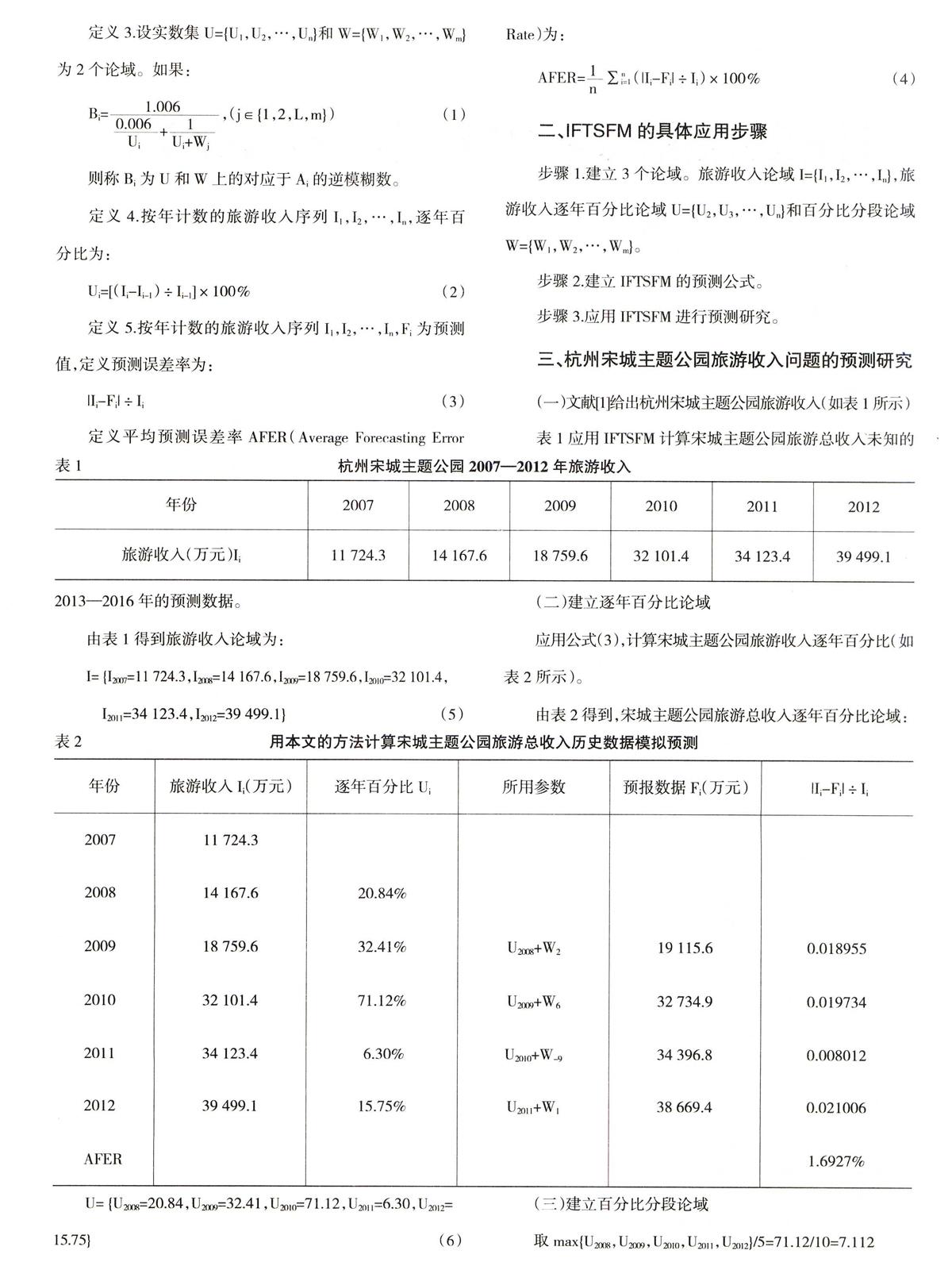
隨機性、缺失相關(guān)的參數(shù)、信息不精確等因素的廣泛存在，使得隨機理論難以有效地解決旅游收入預(yù)測問題。文獻[1]把旅游收入預(yù)測問題看成灰色系統(tǒng)，應(yīng)用GM（1，1）灰色模型研究杭州宋城主題公園旅游收入預(yù)測問題，不僅能進行歷史數(shù)據(jù)的模擬預(yù)測，還能進行未知年數(shù)據(jù)的短中期預(yù)測，是研究該問題的可行方法。Song等[2，3，4]把大學(xué)生入學(xué)率作為模糊系統(tǒng)，用模糊語言表示大學(xué)入學(xué)率的數(shù)據(jù)，首次提出模糊時間序列概念，并提出第一個模糊時間序列模型，應(yīng)用于預(yù)測阿拉巴馬大學(xué)新生入學(xué)率問題。文獻[5]應(yīng)用基于頻率基于密度劃分論域，并首次提出逆模糊數(shù)概念，應(yīng)用提出的模型得到阿拉巴馬大學(xué)新生入學(xué)率預(yù)測的為較小的0.57%；文獻[6]改進文獻[5]的模型，得到同一問題的為很小的0.47%；文獻[7]進一步改進這個模型，得到同一問題的為更小的0.34%，已經(jīng)精確度非常高了。但是，這些模型沒有提及用于研究未知年的數(shù)據(jù)的預(yù)測。文獻[8]不使用文獻[5，6，7]把論域區(qū)間劃分的方法，而是直接應(yīng)用歷史數(shù)據(jù)的逐年百分比和逐年百分比的差，建立論域，應(yīng)用文獻[5，6，7]所使用的逆模糊數(shù)概念，重新建立預(yù)測公式，提出新的模糊時間序列預(yù)測模型NFTSFM（New Fuzzy Time Series Forecasting Model），得到同一問題的為非常小的0.27%，不僅歷史數(shù)據(jù)的模擬預(yù)測精度較高，而且文獻[8]的NFTSFM 能進行未知年數(shù)據(jù)的預(yù)測。本文又對文獻[8]的方法做小的修改，提出改進的模糊時間序列預(yù)測模型IFTSFM（Improved Fuzzy Time Series Forecasting Model）。應(yīng)用IFTSFM重新研究文獻[1]中應(yīng)用GM（1，1）灰色模型來研究杭州宋城主題公園旅游收入預(yù)測問題，得到的歷史數(shù)據(jù)預(yù)測的，IFTSFM比GM（1，1）灰色模型更小。文獻[9]改進了前面的算法，以此應(yīng)用于三亞旅游總收入中，充分證明該方法可行，本文還原新方法應(yīng)用于杭州宋城主題公園旅游收入應(yīng)用于未知年的數(shù)據(jù)的預(yù)測。

一、基本概念

其中Pi和Pi-1分別是i年預(yù)測數(shù)據(jù)和i-1年的預(yù)報數(shù)據(jù)（在本例中，預(yù)測未知年2013年的數(shù)據(jù)時，Pi-1用的是2012年的已知數(shù)據(jù)）。如果ρi是負(fù)數(shù)，說明該年的旅游收入比前一年下降的百分?jǐn)?shù)；如果ρi是零，說明該年的旅游收入和前一年比相同；如果ρi是正數(shù)，說明該年的旅游收入比前一年上升的百分?jǐn)?shù)。

六、關(guān)于應(yīng)用IFTSFM計算未知年2013—2016年間宋城主題公園旅游總收入的預(yù)測數(shù)據(jù)時的說明

當(dāng)計算未知年2013年的預(yù)測數(shù)據(jù)時，需要使用2012年的已知逐年百分比U2012=15.75，百分比分段論域中的元素wj僅取j=-1，0，1，2，3等5個值（把未知年預(yù)測數(shù)據(jù)相對預(yù)測誤差率保持在本文表2中除了特例71.12%外的增長比例，即增長比例保持在15.75%～32.41%之間），得到關(guān)于2013年的5個預(yù)測數(shù)據(jù)。其中粗體字為預(yù)報數(shù)據(jù)，粗體字上方的數(shù)據(jù)為保守預(yù)測數(shù)據(jù)，粗體字下方的數(shù)據(jù)為冒險預(yù)測數(shù)據(jù)。計算未知年2014年的預(yù)測數(shù)據(jù)時，需要使用2013年的預(yù)報數(shù)據(jù)。以此類推，可計算出2014年、2015年和2016年的預(yù)測數(shù)據(jù)，其中粗體字作為預(yù)報數(shù)據(jù)，它的確定如果有決策者的參與可能更符合實際情況。如果預(yù)計發(fā)生和已經(jīng)發(fā)生重大利好或重大利空，調(diào)節(jié)分段論域中的元素的取值便可迅速計算出可能改變的預(yù)測數(shù)據(jù)。

結(jié)束語

杭州宋城主題公園從建成至今，沒有經(jīng)過市場培育期，而是直接步入高速成長期。說明該項目特色鮮明，體現(xiàn)了游客對新時期旅游產(chǎn)品的需求，近年來在我國如麗江、三亞等地都相繼復(fù)制成功，對于杭州宋城主題公園收入預(yù)測分析對于研究整個市場的變化和走勢具有重要作用。而IFTSFM的預(yù)測公式具有結(jié)構(gòu)簡潔，計算工作量小的特點，特別是當(dāng)預(yù)計發(fā)生和已經(jīng)發(fā)生重大利好或重大利空時，調(diào)節(jié)分段論域中的元素的取值便可迅速計算出可能改變的預(yù)測數(shù)據(jù)，以便決策者快速決斷。由于歷史數(shù)據(jù)模擬預(yù)測的平均預(yù)測誤差率非常小，建議應(yīng)用GM（1，1）灰色模型解決歷史數(shù)據(jù)模擬預(yù)測時預(yù)測誤差較大情況下（例如AFER超過5%）時，改用IFTSFM效果更佳。

參考文獻：

[1] 方琳，程乾.基于灰色模型的杭州主題公園游客數(shù)量和經(jīng)濟收入預(yù)測研究[J].經(jīng)濟研究導(dǎo)刊，2014，（15）：223-225.

[2] Song Q.，Chissom B.S.Forecasting enrollments with fuzzy time series—Part I[J].Fuzzy Sets and Systems，1993，（54）：1-9.

[3] Song Q.，Chissom B.S.Forecasting enrollments with fuzzy time series[J].Fuzzy Sets and Systems，1993，（54）：269-277.[4] Song Q.，Chissom B.S.Forecasting enrollments with fuzzy time series—Part II[J].Fuzzy Sets and Systems，1994，（62）：1-8.

[5] T.A.Jilani，S.M.A.Burney，C.Ardil.Fuzzy metric approach for fuzzy time series forecasting based on frequency density based par-

titioning.World Academy of Science[J].Engineering and Technology，2007，（34）：1-6.

[6] Stevenson M.，Porter J.E.Fuzzy time series forecasting using percentage change as the universe of discourse[J].World Academy of Science，

Engineering and Technology，2009，（55）：154-157.

[7] P.Saxena，K.Sharma，S.Easo.Foreeca enrollment based on fuzzy time series with higher forecast accuracy rate[J].International Journal

of Computer Technology and Applications，2012，（3）：957-961.

[8] Wang Hongxu，Guo Jianchun，F(xiàn)eng Hao，Jin Hailong.A new forecasting model of fuzzy time series[J].Applied Mechanics and Ma-

terials，2014：59-63.

[9] 廖民生，張鯤，王鴻緒，李壯，王海豐.基于模糊時間序列模型預(yù)測三亞旅游總收入[J].經(jīng)濟研究導(dǎo)刊，2015，（4）：237-242.

[責(zé)任編輯 王曉燕]