三次參數曲線的區間擴展

李軍成，劉成志（湖南人文科技學院數學系，湖南婁底417000）

?

三次參數曲線的區間擴展

李軍成，劉成志
（湖南人文科技學院數學系，湖南婁底417000）

摘 要：為了在傳統三次參數曲線中引入形狀參數，通過將三次Ferguson曲線、三次Bézier曲線、三次均勻B樣條曲線等傳統三次參數曲線的定義區間由固定區間［0，1］擴展為動態區間［0，α］，構造了3種帶參數α的三次參數曲線，分別稱之為三次α－Ferguson曲線、三次α－Bézier曲線以及三次均勻α－B樣條曲線．所構造的α－曲線是原三次參數曲線的同次擴展，不僅方程結構簡單，繼承了原曲線的性質，而且可通過修改參數α的值實現對曲線形狀的調整，是一種簡單有效的形狀可調參數曲線構造方法．

關 鍵 詞：三次參數曲線；區間擴展；形狀可調

隨著幾何造型工業的發展，常常需要通過改變曲線的形狀來滿足各種幾何造型的需要．Ferguson曲線、Bézier曲線、B樣條曲線等作為傳統幾何造型方法雖然在表示曲線曲面時顯示了較強的能力，但一旦邊界條件或控制頂點固定，用這些方法表示的曲線曲面在形狀修改或調整時就受到了較大的限制，從而制約了其在幾何造型工業中的應用．NURBS曲線雖然能通過權因子對其形狀進行適當調整，但由于采用有理形式，計算比較復雜，使得NURBS曲線在形狀設計與分析中亦存在一定的局限性．近年來，為了克服傳統參數曲線在造型上的不足，國內外許多學者開始構造較為實用的參數曲線模型，其中帶形狀可調的參數曲線逐漸成為研究的熱點．為了構造帶形狀可調的參數曲線，國內外學者提出了許多不同的方法，其中最為常見的有帶形狀參數的多項式曲線［1－5］、帶形狀參數的非多項式曲線［6－10］、帶形狀參數的奇異混合曲線［11－14］．這些方法雖然可通過修改形狀參數值有效調節曲線形狀，但其代價是所構造的曲線模型的次數提高了，或者曲線的方程結構變得復雜．

無論采用何種方法構造形狀可調的參數曲線，其主要目的都是為了在傳統參數曲線中引入形狀參數，通過修改形狀參數的取值實現對曲線形狀的修改或調整，以此來改善傳統參數曲線造型方法的不足．針對形狀可調的參數曲線構造問題，本文提出了在三次Ferguson曲線、三次Bézier曲線、三次均勻B樣條曲線等傳統參數曲線中引入形狀參數的方法，并將其定義區間由固定區間［0，1］擴展為動態區間［0，α］，在這些傳統三次參數曲線中引入形狀參數α，通過調節α的取值，實現對曲線形狀的有效調整．

1 三次α－Ferguson曲線

1．1 三次α－Hermite基函數的構造

傳統三次Ferguson曲線的基函數（也稱為三次Hermite基函數）通常可表示為［15］

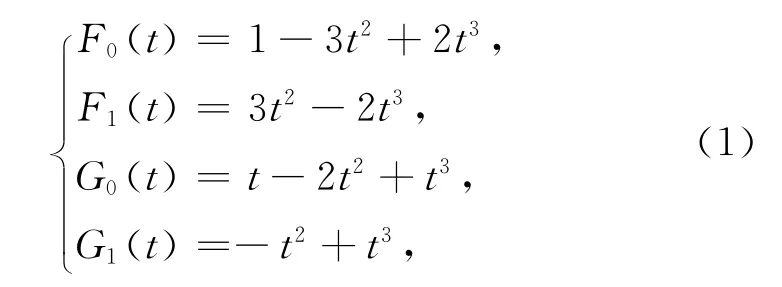
其中0≤t≤1．

由式（1）定義的傳統三次Hermite基函數在端點處滿足

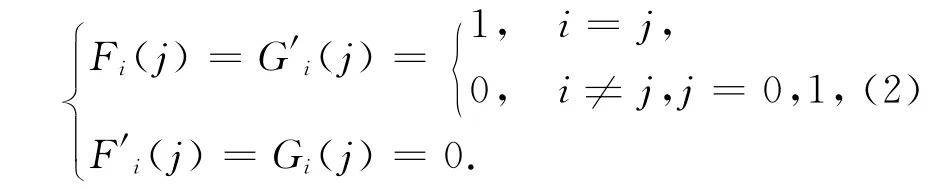
若將傳統三次Hermite基函數的定義區間由t∈［0，1］擴展為動態區間t∈［0，α］（0＜α≤1），則可依據式（2）構造出一種帶參數α的三次Hermite基函數．下面給出具體的構造過程．

設所要構造的4個新基函數為

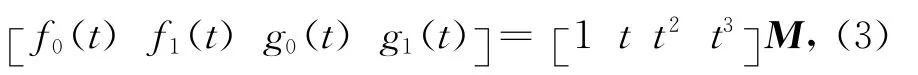
其中，0≤t≤α，0＜α≤1，M為一待定的4×4矩陣．

式（3）兩端對t求導得

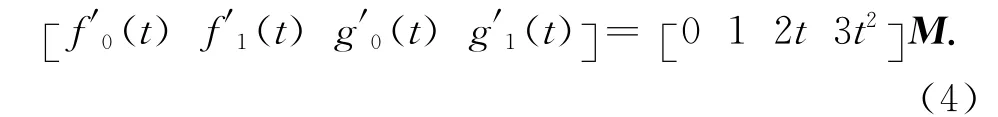
現要求新基函數具有傳統三次Hermite基函數的端點性質，即滿足式（2），有

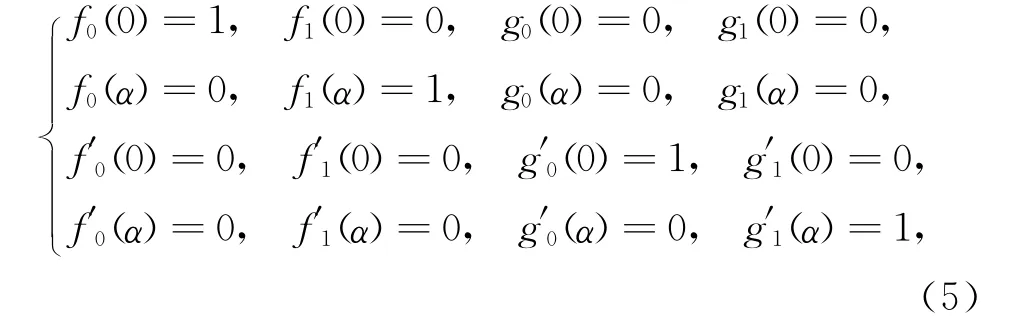
于是，將t＝0與t＝α分別代入式（3）和（4），可得

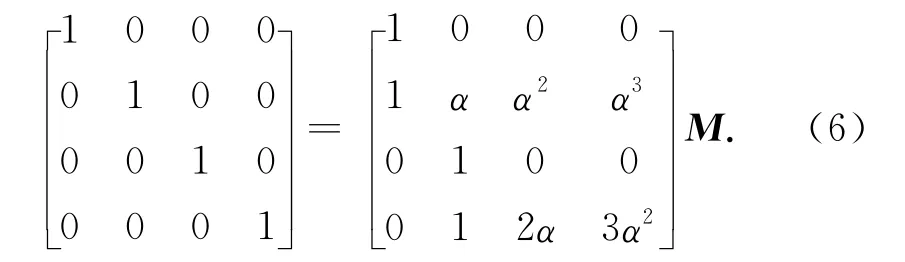
求解式（6）得

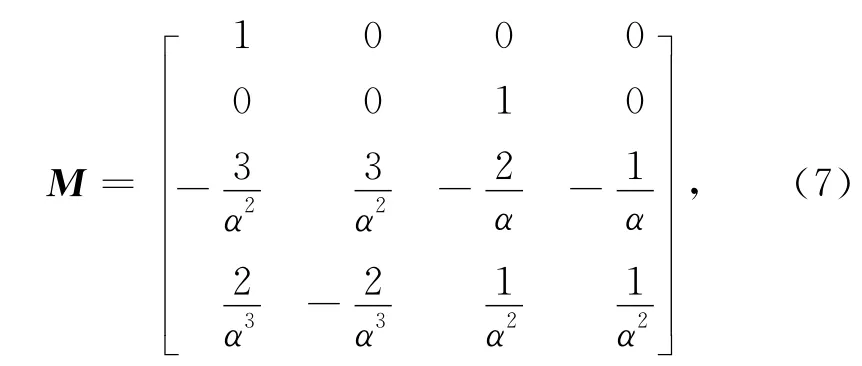
將式（7）代入式（3），可得所要構造的新基函數．

定義1 對于0≤t≤α，0＜α≤1，下列4個關于t的函數

稱為帶參數α的三次Hermite基函數，簡稱為三次α－Hermite基函數．

1．2 三次α－Ferguson曲線的定義及其性質

基于三次α－Hermite基函數，可定義如下帶參數α的三次Ferguson曲線．

定義2 對于0≤t≤α，0＜α≤1，給定曲線段的首、末端點ai及其切矢a′i（i＝0，1），稱曲線

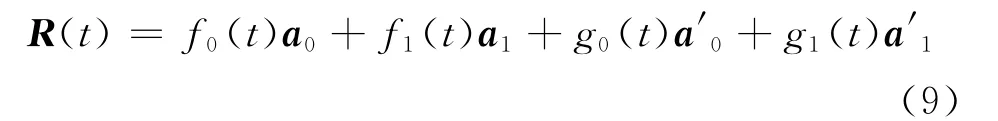
為帶參數α的三次Ferguson曲線，簡稱為三次α－Ferguson曲線，其中fi（t）與gi（t）（i＝0，1）為式（8）定義的三次α－Hermite基函數．

由式（5）與（9），可得三次α－Ferguson曲線具有如下插值性：

定理1 由式（9）定義的三次α－Ferguson曲線插值于給定的首、末端點及其切矢，即

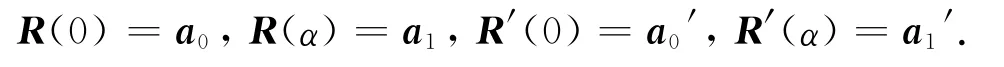
注1 定理1表明，三次α－Ferguson曲線與傳統三次Ferguson曲線具有完全相同的插值性．特別地，當α＝1時，三次α－Ferguson曲線即為傳統三次Ferguson曲線．因此，三次α－Ferguson曲線是傳統三次Ferguson曲線的一種同次擴展．當曲線段的首、末端點及其切矢給定時，傳統三次Ferguson曲線的形狀無法修改，但三次α－Ferguson曲線的形狀可通過修改參數α的值進行調節，從而為曲線的設計提供便利．

當曲線段的首、末端點及其切矢固定時，參數α對三次α－Ferguson曲線的形狀有如下影響：

定理2 固定曲線段的首、末端點ai及其切矢ai′（i＝0，1），則參數α的取值越大，三次α－Ferguson曲線越遠離邊a0a1．

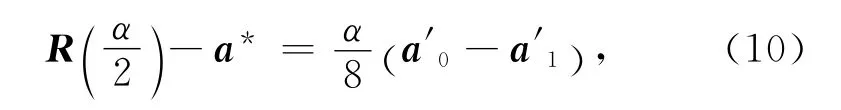
式（10）兩邊同時取范數有

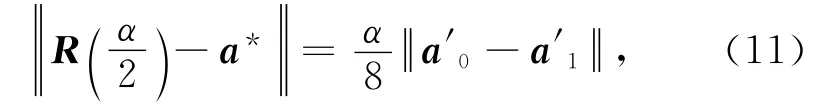
圖1為曲線段的首、末端點及其切矢固定時參數α取不同值時的三次α－Ferguson曲線，圖中各曲線由外到內所取的參數分別為a＝0．2，0．4，0．6，0．8，1．0．

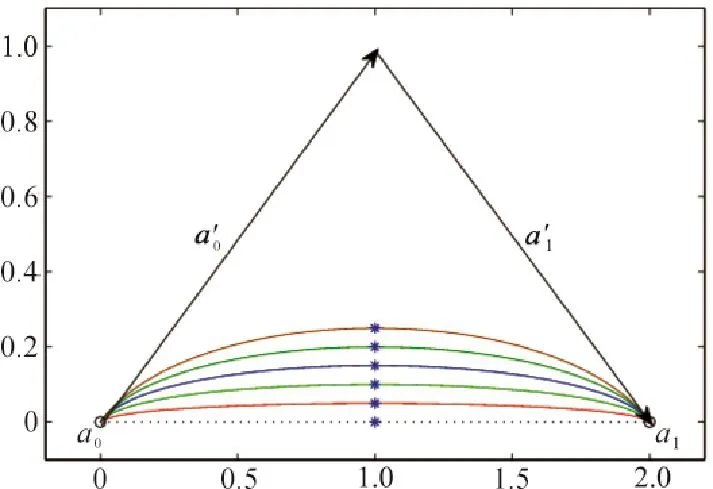
圖1　參數α取不同值時的三次α－Ferguson曲線Fig．1 Cubicα－Ferguson curves with differentα

2 三次α－Bézier曲線

2．1 三次α－Bernstein基函數的構造

傳統三次Bézier曲線的基函數（也稱為三次Bernstein基函數）通常可表示為［15］

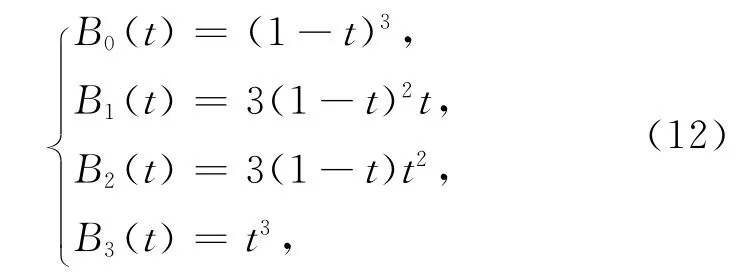
其中0≤t≤1．

由式（12）定義的傳統三次Bernstein基函數在端點處滿足：

若將傳統三次Bernstein基函數的定義區間由t∈［0，1］擴展為動態區間t∈［0，α］（0＜α≤1），則依據式（13）可構造出一種帶參數α的三次Bernstein基函數．下面給出具體的構造過程．

設所要構造的4個新基函數為

式中0≤t≤α，0＜α≤1，M為一待定的4×4矩陣．

式（14）兩端對t求導得

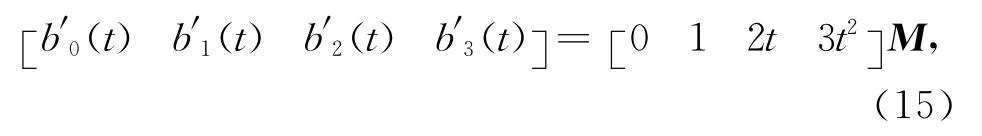
現要求新基函數具有傳統三次Bernstein基函數的端點性質式（13），即有

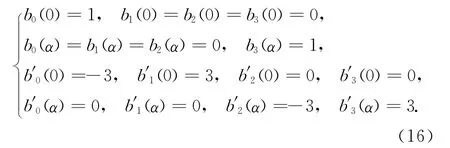
將t＝0與t＝α分別代入式14）和（15），可得

求解式（17），可得

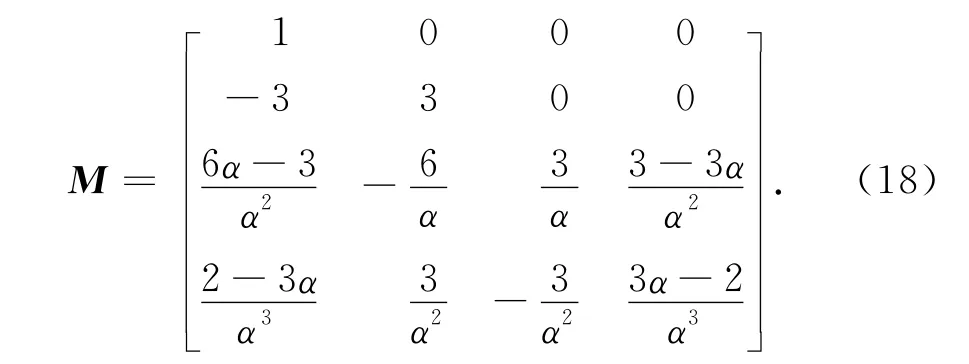
將式（18）代入式（14），可得所要構造的新基函數．

定義3 對于0≤t≤α，0＜α≤1，下列關于t 的4個函數：

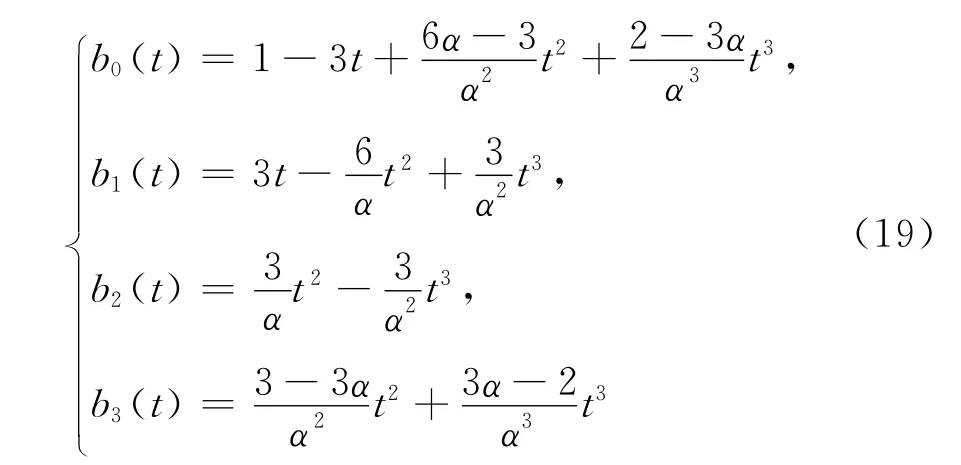
稱為帶參數α的三次Bernstein基函數，簡稱為三次α－Bernstein基函數．

定理3 由式（19）定義的三次α－Bernstein基函數具有如下性質：

（1）非負性：bi（t）≥0（i＝0，1，2，3）；

（2）混合性：b0（t）＋b1（t）＋b2（t）＋b3（t）≡1；

（3）對稱性：bi（t）＝b3－i（α－t）（i＝0，1，2，3）；

（4）端點性質：三次α－Bernstein基函數在端點處滿足式（16）．

證明 （1）式（19）可改寫為

當0≤t≤α，0＜α≤1時，a－t≥0，1－α≥0．故由式（20）可得bi（t）≥0（i＝0，1，2，3）．

（2）由式（19）經簡單計算可得混合性成立．

（3）由式（20）得對稱性成立．

（4）由三次α－Bernstein基函數的構造可知，端點性顯然成立．

2．2 三次α－Bézier曲線的定義及其性質

基于三次α－Bernstein基函數，可定義如下帶參數α的三次Bézier曲線：

定義4 對于0≤t≤α，0＜α≤1，給定平面上或空間中4個控制頂點pi（i＝0，1，2，3），稱曲線

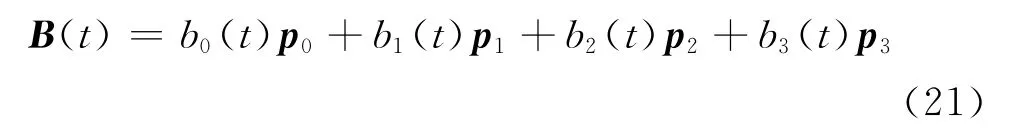
為帶參數α的三次Bézier曲線，簡稱為三次α－Bézier曲線，其中bi（t）（i＝0，1，2，3）為式（19）定義的三次α－Bernstein基函數．

定理4 由式（21）定義的三次α－Bézier曲線具有如下性質：

（1）端點性質：三次α－Bézier曲線插值于首、末控制頂點，且與控制多邊形的首、末邊相切，即有

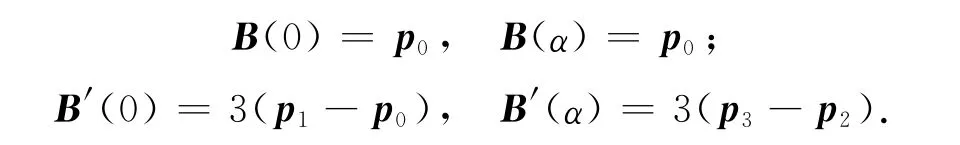
（2）對稱性：對于相同的參數α，由控制頂點pi與p3－i（i＝0，1，2，3）分別確定的三次α－Bézier曲線重合，只是參數化方向相反，即有

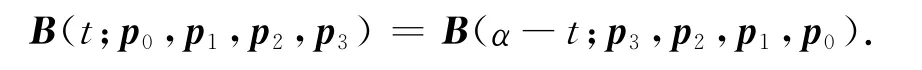
（3）幾何不變性：三次α－Bézier曲線的形狀和位置與坐標系的選取無關．

（4）凸包性與保凸性：三次α－Bézier曲線被完全包含在由控制頂點pi（i＝0，1，2，3）形成的凸包內．當控制多邊形為凸時，三次α－Bézier曲線也為凸．

證明 （1）由式（16）與（21）可得

（2）由三次α－Bernstein基函數的對稱性與式（21）可得

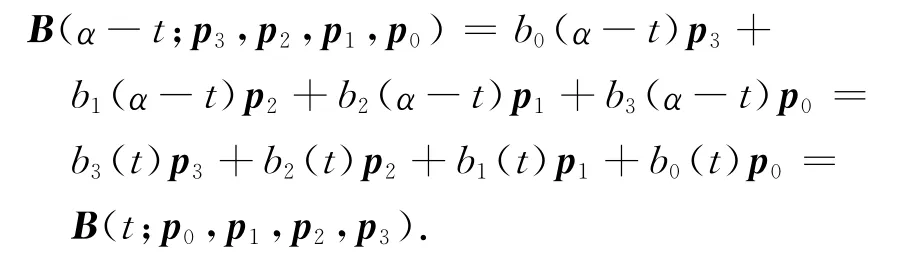
（3）由于式（21）為一矢量函數，故三次α－Bézier曲線的形狀和位置與坐標系的選取無關．

（4）由于三次α－Bernstein基函數bi（t）（i＝0，1，2，3）滿足非負性與權性，而式（21）是控制頂點pi關于bi（t）（i＝0，1，2，3）的加權線性組合，故三次α－Bézier曲線被完全包含在由控制頂點pi（i＝0，1，2，3）形成的凸包內．特別地，當控制多邊形為凸時，三次α－Bézier曲線也為凸．

注2 定理4表明，三次α－Bézier曲線與傳統三次Bézier曲線具有完全相同的性質．特別地，當α＝1時，三次α－Bézier曲線即為傳統三次Bézier曲線．因此，三次α－Bézier曲線是傳統三次Bézier曲線的同次擴展．當控制頂點保持不變時，傳統三次Bézier曲線的形狀無法修改，但三次α－Bézier曲線的形狀可通過修改參數α的值進行調節，從而為曲線的設計提供了便利．

當控制頂點固定時，參數α對三次α－Bézier曲線的形狀有如下影響．

定理5 設給定的控制頂點pi（i＝0，1，2，3）不共線，且p1與p2位于邊p0p3的同側，則參數α的取值越大，三次α－Bézier曲線越靠近控制多邊形．

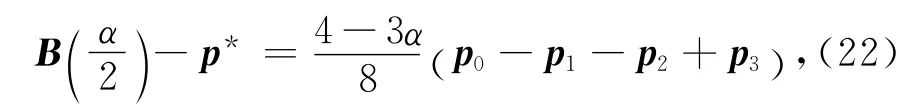
式（22）兩邊同時取范數有

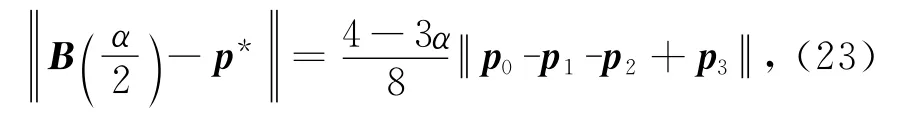
圖2為控制頂點固定時，參數α取不同值時的三次α－Bézier曲線，圖中各曲線由外到內所取的參數分別為α＝0．2，0．4，0．6，0．8，1．0．

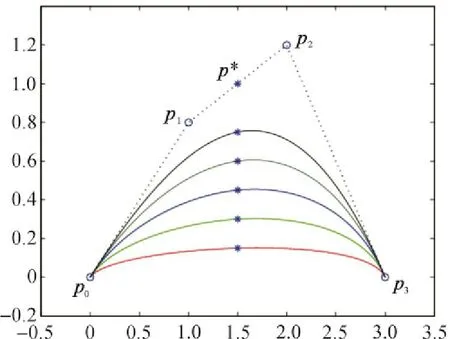
圖2　參數α取不同值時的三次α－Bézier曲線Fig．2 Cubicα－Bézier curves with differentα

3 三次均勻α－B樣條曲線

3．1 三次均勻α－B樣條基函數的構造

傳統三次均勻B樣條基函數的表達式可寫為［15］

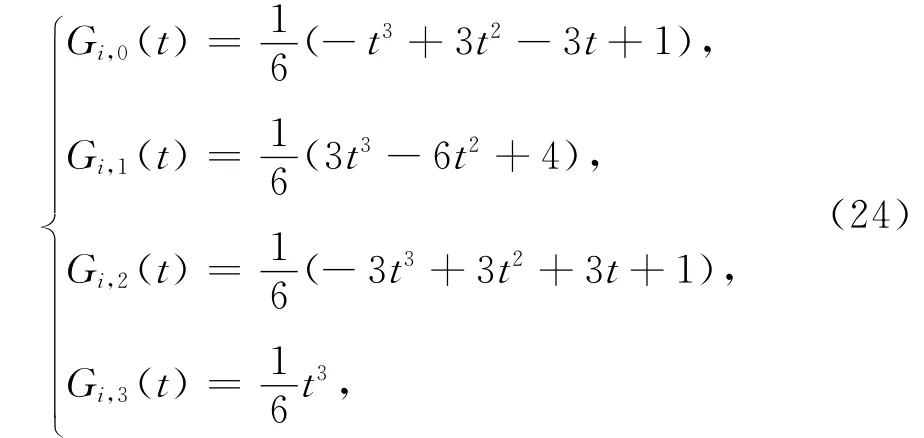
其中，0≤t≤1．其在端點處滿足

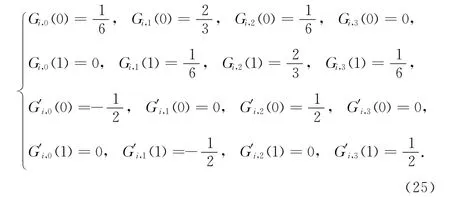
若將其定義區間由t∈［0，1］擴展為動態區間t∈［0，αi］（0＜αi≤1），則可依據式（25）構造出一種帶參數的三次均勻B樣條基函數．下面給出具體的構造過程．

設所要構造的新基函數為

式中0≤t≤αi，0＜αi≤1，M為一待定的4×4矩陣．

式（26）兩端分別對t求導可得

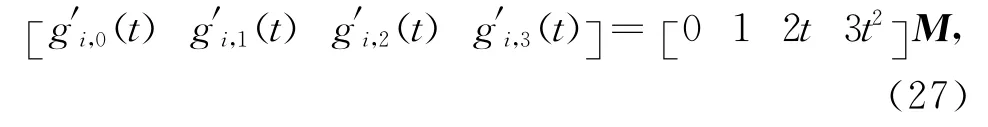
現要求新基函數具有傳統三次Bernstein基函數的端點性質式（25），即滿足

將t＝0與t＝αi分別代入式（26）與（27），則由式（28）可得

求解式（29）得

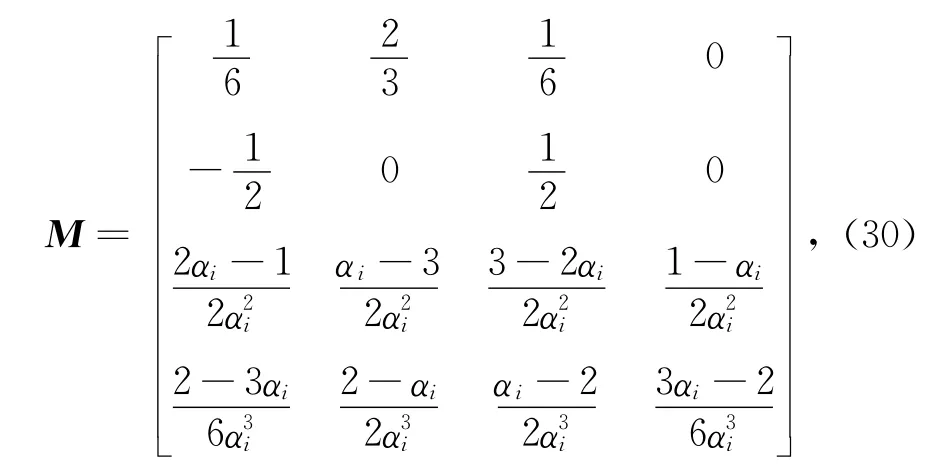
將式（30）代入式（26），可得所要構造的新基函數．

定義5 對于0≤t≤αi，0＜αi≤1，下列關于t的函數

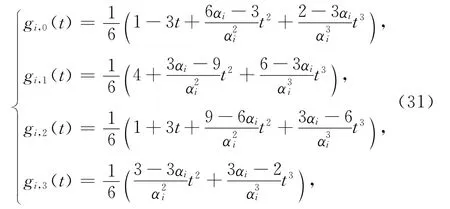
稱為帶參數αi的三次均勻B樣條基函數，簡稱為三次均勻α－B樣條基函數．

定理6 由式（31）定義的三次均勻α－B樣條基函數具有如下性質：

（1）非負性：gi，j（t）≥0（j＝0，1，2，3）；

（2）混合性：

（3）對稱性：

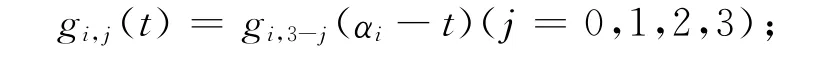
（4）端點性質：三次均勻α－B樣條基函數在端點處滿足式（26）；

（5）單調性：固定t∈［0，αi］（0＜αi≤1），g0（t）與g1（t）關于參數ai單調遞減，g2（t）與g3（t）關于參數αi單調遞減．

證明 （1）固定αi∈（0，1］，當0≤t≤αi時，由式（29）可得

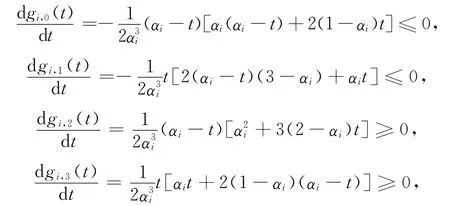
故gi，0（t）與gi，1（t）關于變量t單調遞減，gi，2（t）與gi，3（t）關于變量t單調遞增，于是有

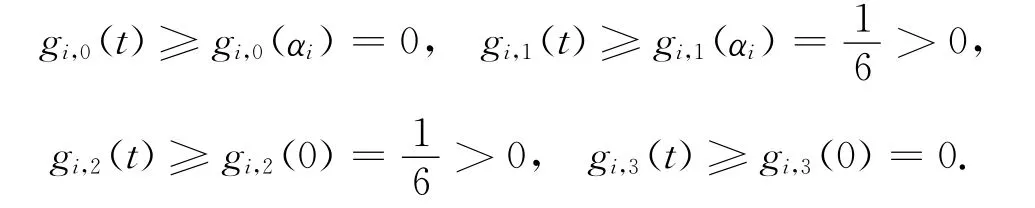
（2）由式（31）經簡單推導，可得混合性成立．

（3）由式（31）經簡單計算，可得對稱性成立．

（4）由三次均勻α－B樣條基函數的構造過程可知，端點性質顯然成立．

（5）固定t∈［0，αi］（0＜αi≤1），由式（31）可得

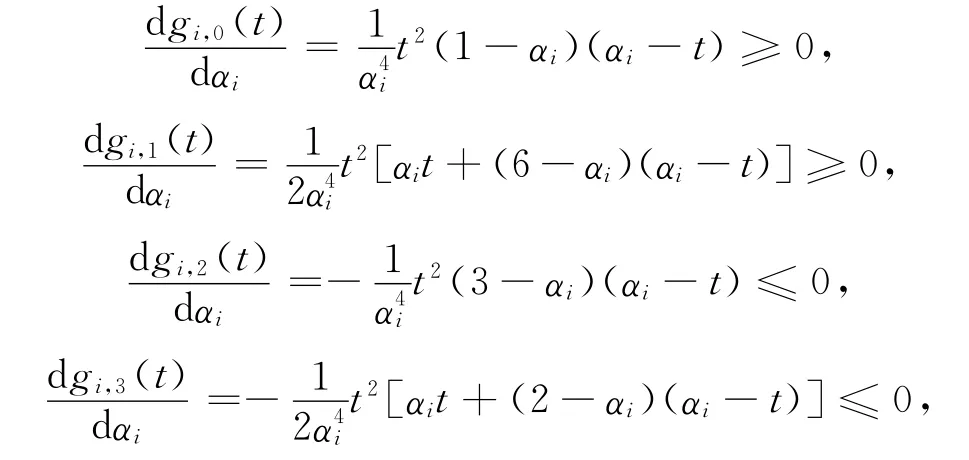
于是，gi，0（t）與gi，1（t）關于參數αi單調遞增，gi，2（t）與gi，3（t）關于參數αi單調遞減．

3．2 三次均勻α－B樣條曲線的定義及其性質

基于三次均勻α－B樣條基函數，可定義如下帶參數αi的三次均勻B樣條曲線：

定義6 對于0≤t≤αi，0＜αi≤1，給定平面上或空間中n＋1控制頂點qj（j＝0，1，2，…，n），稱分段曲線

為帶參數αi的三次均勻B樣條曲線，簡稱為三次均勻α－B樣條曲線，其中gi，j（t）（j＝0，1，2，3）為式（31）定義的三次均勻α－B樣條基函數．

定理7 由式（32）定義的三次均勻α－B樣條曲線具有如下性質：

（1）連續性：三次均勻α－B樣條曲線滿足C1連續，即滿足

（2）對稱性：對于相同的參數αi，分別由控制頂點確定的第i段三次均勻α－B樣條曲線重合，只是參數化方向相反，即有

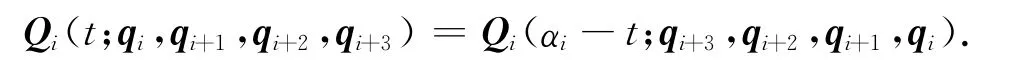
（3）幾何不變性：三次均勻α－B樣條曲線的形狀和位置與坐標系的選取無關．

（4）凸包性與保凸性：第i段三次均勻α－B樣條曲線被完全包含在由控制頂點qi＋j（j＝0，1，2，3）形成的凸包內．特別地，當所有控制頂點形成一個閉凸多邊形時，三次均勻α－B樣條曲線也為一條凸曲線．

證明 （1）由式（28）與（32）可得

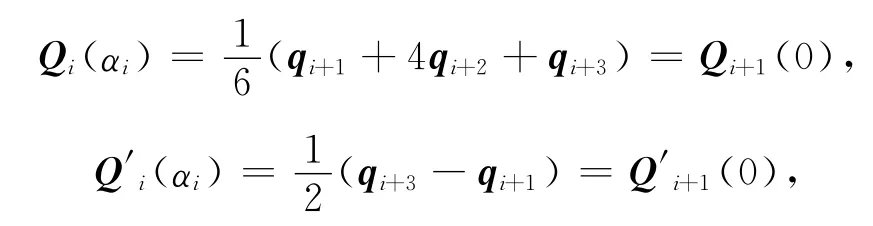
即三次均勻α－B樣條曲線滿足C1連續．

（2）由三次均勻α－B樣條基函數的對稱性與式（32）可得

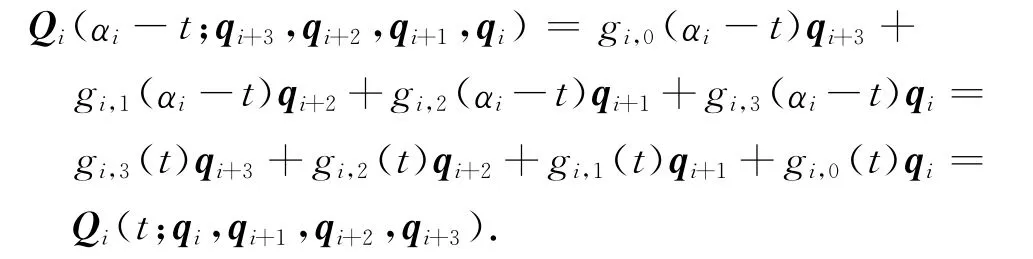
（3）由于式（32）為一矢量函數，故三次均勻α－B樣條曲線的形狀和位置與坐標系的選取無關．

（4）由于三次均勻α－B樣條基函數gi，j（t）（j＝0，1，2，3）滿足非負性與權性，而第i段三次均勻α－B樣條曲線Qi（t）是控制頂點qi＋j關于gi，j（t）（j＝0，1，2，3）的加權線性組合，故第i段三次均勻α－B樣條曲線被完全包含在由控制頂點qi＋j（j＝0，1，2，3）形成的凸包內．特別地，當所有控制頂點形成一個閉凸多邊形時，三次均勻α－B樣條曲線也為一條凸曲線．

注3 定理7表明，三次均勻α－B樣條曲線與傳統三次均勻B樣條曲線具有幾乎完全相同的性質（連續性除外，傳統三次均勻B樣條曲線滿足C2連續）．特別地，當α＝1時，三次均勻α－B樣條曲線即為傳統三次均勻B樣條曲線．因此，三次均勻α－B樣條曲線是傳統三次均勻B樣條曲線的同次擴展．當所有控制頂點保持不變時，傳統三次均勻B樣條曲線的形狀無法修改，但三次均勻α－B樣條曲線的形狀可通過修改參數α1的值進行調節，從而為曲線的設計提供了便利．

當所有控制頂點qj（j＝0，1，2，…，n）固定時，只修改參數α1的值，則只會對第i段三次均勻α－B樣條曲線Qi（t）的形狀有影響，而對其他曲線段無任何影響，即參數α1對整條三次均勻B樣條曲線的形狀具有局部調節作用．進一步，當第i段三次均勻α－B樣條曲線的控制頂點qi＋j（j＝0，1，2，3）保持不變時，參數αi對曲線段的形狀有如下影響：

定理8 設第i段三次均勻α－B樣條曲線Qi（t）的控制頂點qi＋j（j＝0，1，2，3）不共線，且qi＋1與qi＋2位于邊qiqi＋3的同側，則參數α1的取值越大，曲線段越靠近其控制多邊形．

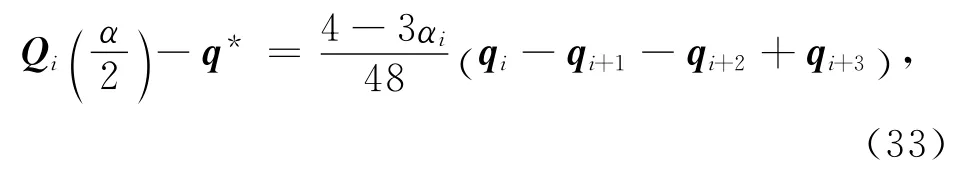
式（33）兩邊同時取范數有

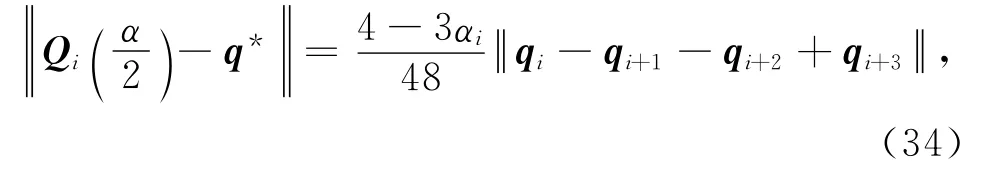
由式（34）可知，參數αi取值越大的值越小，則越靠近q＊，即第i段三次均勻α－B樣條曲線Qi（t）越靠近其控制多邊形．

圖3為當所有控制頂點固定時，參數αi對三次均勻α－B樣條曲線的局部調節，圖中第2段曲線由外到內參數α2＝0．3，0．6，0．9，其余各段曲線參數均為0．6．

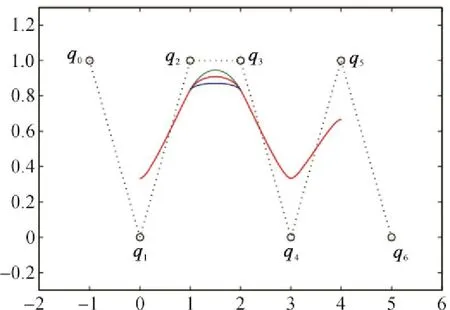
圖3　參數對三次均勻α－B樣條曲線的局部調節Fig．3 Local adjustment of the parameter on a cubic uniformα－B－spline curve

當所有控制頂點qj（j＝0，1，2，…，n）固定時，若將所有三次均勻α－B樣條曲線段Qi（t）（i＝0，1，2，…，n－3）的參數取為同一值α，即取αi＝α（i＝0，1，2，…，n－3），則可通過修改參數α的值實現對三次均勻α－B樣條曲線的整體調節．圖4為當所有控制頂點固定時，參數αi＝α（i＝0，1，2，3）對三次均勻α－B樣條閉曲線的整體調節圖，圖中短虛線對應的參數α＝0．3，長虛線對應的參數α＝0．6，實線對應的參數α＝1．0．

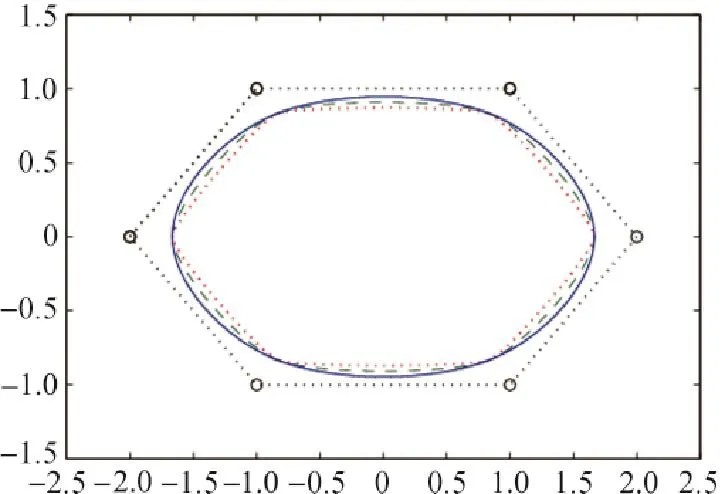
圖4　參數對三次均勻α－B樣條閉曲線的調節Fig．4 Global adjustment of the parameter on a closed cubic uniformα－B－spline curve

4 三次α－曲線之間的關系

三次α－Ferguson曲線的定義式式（9）可改寫成矩陣形式：

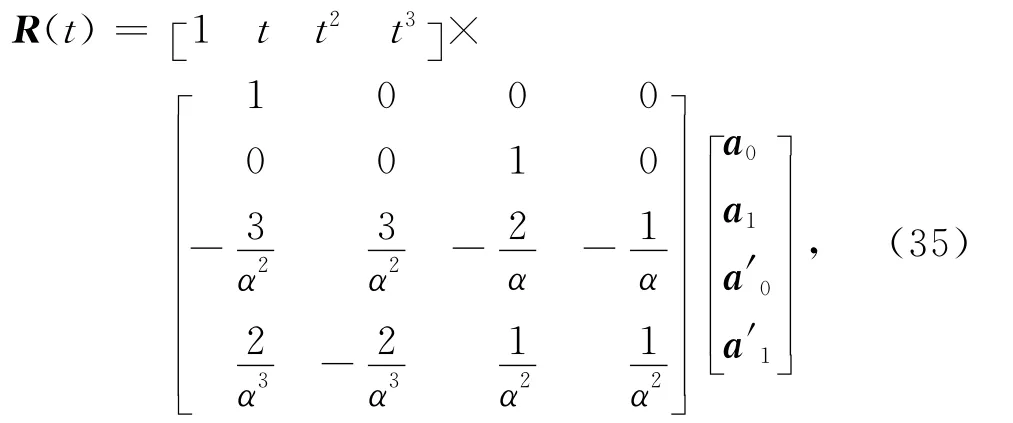
式中0≤t≤α，0＜α≤1．

三次α－Bézier曲線的定義式式（21）可改寫成矩陣形：

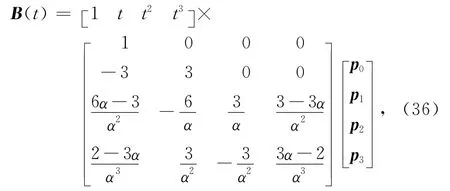
式中0≤t≤α，0＜α≤1．

若僅考慮一段曲線，則三次均勻α－B樣條曲線的定義式式（32）可改寫成矩陣形式：

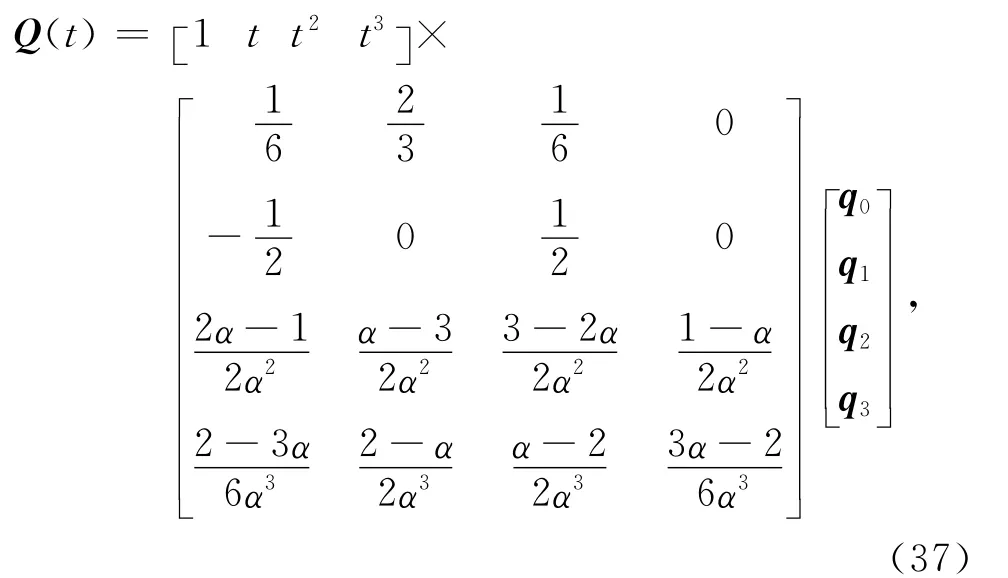
式中0≤t≤α，0＜α≤1．

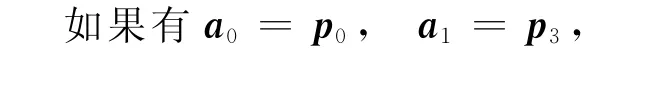
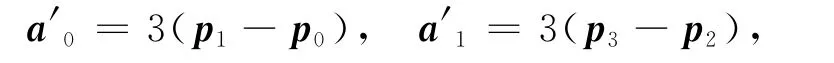
由式（35）與（36），三次α－Ferguson曲線可轉化為三次α－Bézier曲線．

如果有

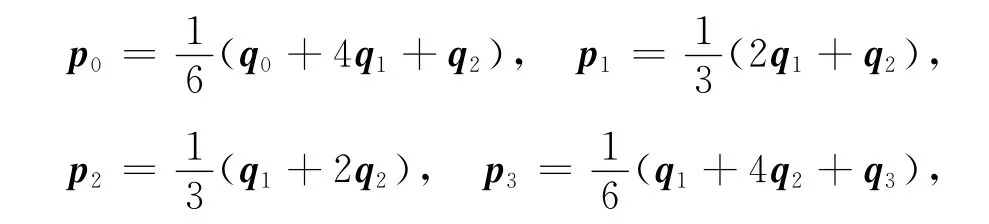
由式（36）與（37），則三次α－Bézier曲線可轉化為三次均勻α－B樣條曲線．

同樣，如果有

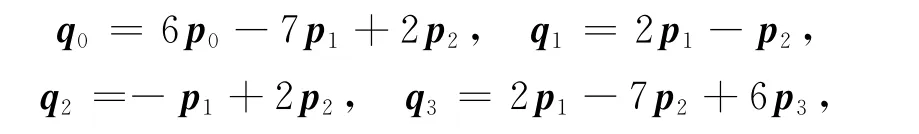
則三次均勻α－B樣條曲線可轉化為三次α－Bézier曲線．

5 結 語

為了構造形狀可調的參數曲線，將三次Ferguson曲線、三次Bézier曲線、三次均勻B樣條曲線等傳統參數曲線的定義區間由固定區間［0，1］擴展為動態區間［0，α］，構造了3種帶參數α的三次曲線．所構造的新曲線不僅完全繼承了傳統三次參數曲線的性質，而且可通過修改參數α的值調整其形狀．另外，所構造的新曲線均為多項式模型，且為相應三次參數曲線的同次擴展，相較其他類似的曲線模型，方程結構更簡潔，因此是一種簡單有效的帶形狀參數的曲線造型方法．目前眾多CAD／CAM系統均采用了三次Ferguson曲線、三次Bézier曲線、三次均勻B樣條曲線等參數曲線，本文所構造的新曲線與傳統參數曲線的方程結構非常接近，因此可將其應用于相應的CAD／CAM系統中．進一步，可繼續研究所構造的新曲線的具體算法，也可將所構造的新曲線推廣到曲面形式，將另文討論．

參考文獻（References）：

［1］ YAN Lanlan，LIANG Qiongfeng．An extension of the Bézier model［J］．Applied Mathematics and Computation，2011，218（6）：2863－2879．

［2］ CHEN Jun，WANG Guojin．A new type of the generalized Bézier curves［J］．Applied Mathematics：A Journal of Chinese Universities，2011，26（1）：47－56．

［3］ CAO Juan，WANG Guozhao．Non－uniform B－splinecurves with multiple shape parameters［J］．Journal of Zhejiang U－niversity SCIENCE C，2011，12（10）：800－808．

［4］ FAN Feilong，ZENG Xiaoming．S－λbases and S－λcurves［J］．Computer－Aided Design，2012，44（11）：1049－1055．

［5］ QIN Xinqiang，HU Gang，ZHANG Nianjun，et al．A novel extension to the polynomial basis functions describing Bézier curves and surfaces of degree n with multiple shape parameters［J］．Applied Mathematics and Computation，2013，223：1－16．

［6］ LIU Xumin，XU Weixiang，GUAN Yong，et al．Hyperbolic polynomial uniform B－spline curves and surfaces with shape parameter［J］．Graphical Models，2010，72（1）：1－6．

［7］ YAN Lanlan，LIANG Jiongfeng．A class of algebraictrigonometric blended splines［J］．Journal of Computational and Applied Mathematics，2011，235（6）：1713－1729．

［8］ HAN Xuli，ZHU Yunpeng．Curve construction based on five trigonometric blending functions［J］．BIT Numerical Mathematics，2012，52（4）：953－979．

［9］ LI Juncheng．A class of cubic trigonometric Bézier curve with a shape parameter［J］．Journal of Information and Computational Science，2013，10（10）：3071－3078．

［10］ BASHIR U，ABBSA M，ALI J M．The G2and C2rational quadratic trigonometric Bézier curve with two shape parameters with applications［J］．Applied Mathematics and Computation，2013，219（20）：10183－10197．

［11］ PAPP I，HOFFMANN M．C2and G2continuous spline curves with shape parameters［J］．Journal for Geometry and Graphics，2007，11（2）：179－185．

［12］ XU Gang，WANG Guozhao．Extended cubic uniform B－spline andα－B－spline［J］．Acta Automatica Sinica，2008，34（8）：980－984．

［13］ JUHáSZ I，HOFFMANN M．Surface interpolationwith local control by linear blending［J］．Annales

Mathematicae et Informaticae，2009，36（1）：77－84．

［14］ ZHU Yunpeng，HAN Xuli，HAN Jing．Quartic trigonometric Bézier curves and shape preserving interpolation curves［J］．Journal of Computational Information Systems，2012，8（2）：905－914．

［15］ 朱心雄．自由曲線曲面造型技術［M］．北京：科學出版社，2000．ZHU Xinxiong．Technology of Free Curves and Surfaces Modeling［M］．Beijing：Science Press，2000．

Interval extension of the cubic parametric curves

LI Juncheng，LIU Chengzhi（Department of Mathematics，Hunan University of Humanities，Science and Technology，Loudi 417000，Hunan Province，China）

Journal of Zhejiang University（Science Edition），2016，43（1）：079－086

Abstract：In order to introduce the shape parameter into the traditional cubic parametric curves，definition interval of cubic Ferguson curve，cubic Bézier curve and cubic uniform B－spline curve is extended from a fixed interval［0，1］to a dynamic interval［0，α］．Then three cubic parametric curves with parameterαare constructed，which are named cubicα－Ferguson curve，cubicα－Bézier curve and cubic uniformα－B－spline curve，respectively．The proposed threeα－curves are extensions of the corresponding cubic parametric curves．They not only have simple structure，inherit the properties of the corresponding cubic parametric curves，but also can be adjusted by altering the value of parameterα．Therefore，the proposed method is a simple and effective method for constructing shape－adjustable parametric curves．

Key Words：cubic parametric curves；interval extension；shape－adjustable

作者簡介：李軍成（1982－），男，博士，副教授，主要從事計算機輔助幾何設計及其應用研究，E－mail：lijuncheng82＠126．com．

基金項目：湖南省教育廳資助科研項目（14B099）；湖南省自然科學基金資助項目（13JJ6081）．

收稿日期：2015－03－26．

DOI：10．3785／j．issn．1008－9497．2016．01．014

中圖分類號：O 241．5；TP391

文獻標志碼：A

文章編號：1008－9497（2016）01－079－08