非對易空間中的三維諧振子Wigner函數

王興忠，李 康（．寧波大紅鷹學院，浙江寧波3575；．杭州師范大學物理系，浙江杭州3）

?

非對易空間中的三維諧振子Wigner函數

王興忠1，李 康2
（1．寧波大紅鷹學院，浙江寧波315175；2．杭州師范大學物理系，浙江杭州311121）

摘 要：概述了量子相空間分布函數引入的依據、非對易空間與非對易相空間的基本性質；討論了非對易空間中量子相空間分布函數的具體表現形式；給出了在對易空間和非對易相空間中定態Schr?dinger方程和Wigner函數能量本征方程的表述式；并對照了它們在3種空間中的演變規律．最后，給出了在三維非對易空間和非對易相空間中諧振子模型Wigner函數的表達式．研究結果可以應用到更復雜的物理體系中．

關 鍵 詞：非對易時空；相空間分布函數；Wigner分布函數

在量子力學的相空間框架中，量子現象可以用盡可能多的經典語言來描述．這種描述只要求處理常數方程而不是算符方程．

在非對易空間中量子相空間分布函數是一個重要的研究領域．1948年MOYAL利用量子相空間中的Wigner分布函數，探討了非對易空間問題，找到了一種量子化方法，即Moyal星乘法．此方法和之前已有的量子化方法（正則量子化、路徑積分量子化等）等價．與其他量子相空間分布函數相比，Wigner分布函數可以進行莫爾星乘量子化，即可以作為量子力學的一種表述形式．

許多復雜的物理模型可以分解為諧振子的組合，而諧振子的Wigner函數有明確的表達形式，所以對此進行深入研究具有十分重要的意義．

1 對易空間中的量子相空間分布函數

1．1 對易空間中的位置與動量關系

對易空間中的位置與動量關系滿足：

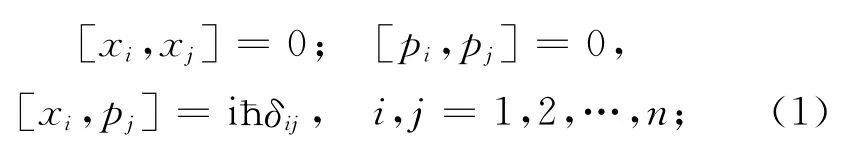
量子相空間分布函數F（q，p，t）的定義式［1］：

根據Cohen分類表［2］，量子相空間分布函數F（q，p，t）的一般類型可以用如下方程來定義：

1．2 三維對易空間中的Wigner函數定義式

由式（3），取f（ξ，η）＝1，即得Wigner分布函數［3］：

此空間中的Wigner函數能量本征方程由星乘形式表示，為

已知，三維諧振子（其質量為μ，頻率為ω）的Hamilton量為

其在坐標表象下的Schr?dinger方程為

解此方程可得［4］：

把式（8）直接代入式（4）或式（5），都可以得到三維對易相空間中諧振子的Wigner函數表示式［5］，即

2 非對易空間中的三維諧振子Wigner函數［6］

非對易空間（NC space）中的位置與動量關系滿足［7］：

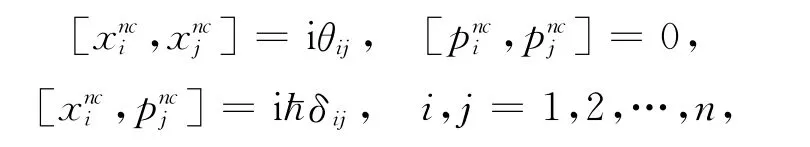
其中，

非對易空間中的薛定諤方程通常可表示為

此空間中相關Bopp變換的表示式為

參照式（3），有非對易空間的三維Wigner分布函數表達式：

非對易空間中關于Wigner函數的能量本征方程為

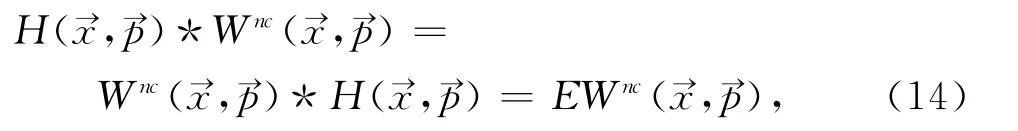
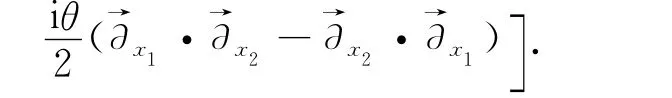
Wigner分布函數的能量本征方程經過式（12）Bopp變換后，可寫成如下形式：

在非對易空間中，三維諧振子的Hamiltonian為（令μ＝1，ω＝1）：

把式（16）代入式（15），經計算可得三維諧振子在非

對易空間中用對易空間中的坐標與動量表示的Wigner函數：

3 非對易相空間中三維諧振子的Wigner函數［8］

非對易相空間（NC phasc space）中的位置與動量的關系滿足：

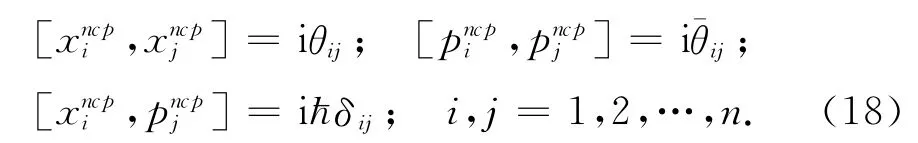
非對易相空間中的定態Schr?dinger方程可以表示為

此空間中相應的Bopp變換式：

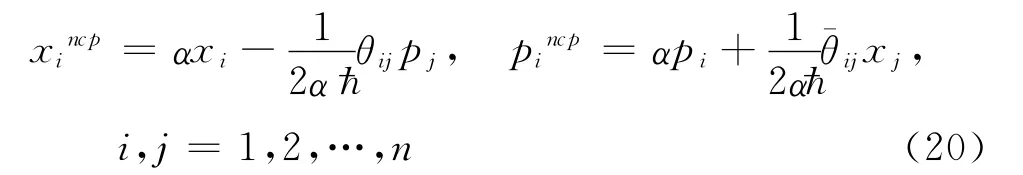
同樣，三維非對易相空間中的Wigner分布函數可以表示為

非對易空間中關于Wigner分布函數的能量本征方程可表示為

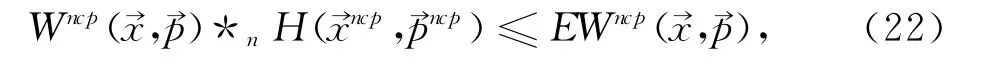
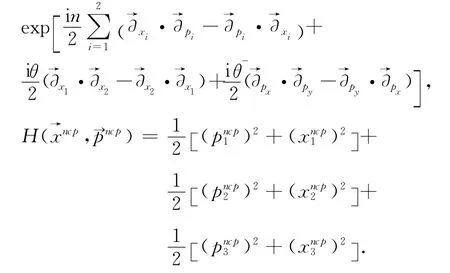
把三維諧振子的波函數式式（8）代入非對易相空間Wigner分布函數的定義式式（21），或利用求解非對易相空間中Wigner分布函數的本征方程式（22），都可以得到三維諧振子在非對易相空間中的Wigner函數：

再利用Bopp變換，最后用對易空間中的坐標與動量來表示處于非對易相空間中的三維諧振子Wigner分布函數，可得如下式子：

4 結 論

簡析了量子相空間分布函數引入的基本依據．系統概述了常規的對易空間、非對易空間與非對易相空間的基本性質．給出了在這3種空間中的定態Schr?dinger方程各自的表達式以及Wigner函數能量本征方程的表達式，從中可以清晰地看到這些表示式在3種空間中的遞進演變規律．最后，給出了在非對易空間和非對易相空間中的三維諧振子的Wigner分布函數表達式．

參考文獻（References）：

［1］ LEE H W．Theory and application of the quantum phase－space distribution functions［J］．Physics Reports，1995，259：147－211．

［2］ COHEN L．Generalized phose space distributions［J］．J Math Phys，1966（7）：781．

［3］ WIGNER E．On the quantum correction for thermodynamic equilibrium［J］．Phys Rev，1932，40：749－759．

［4］ 喀興林．高等量子力學［M］．第2版，北京：高等教育出版社，2001：118．KA Xinglin．Advanced Quantum Mechanics［M］．2nd ed，Beijing：Higher Education Press，2001：118．

［5］ 馬凱，李康，王劍華．非對易相空間中的Moyal方程和Wigner函數［J］．浙江大學學報：理學版，2011，38（2）：163－167．MA Kai，LI Kang，WANG Jianhua．Moyal equation and Wigner function in non－commutative phase space ［J］．Journal of Zhejiang University：Science Edition，2011，38（2）：163－167．

［6］ LI Kang，WANG Jianhua，DULAT S，et al．Wigner functions for Klen－Gordon oscillator in non－commutative space［J］．Int J Theor Phys，2010，49：134－143．

［7］ LI Kang，DULAT S．The Aharonov－Bohm effect in non－commutative quantum mechanics［J］．Eur Phys J，2006，C46：825－828．

［8］ LI Kang，WANG Jianhua，CHEN Chiyi．Representation of noncommutative phase space［J］．Modern Physics Letter A，2005，20（28）：2165－2174．

The Wigner function of the three dimensional harmonic oscillator in non－commutative space

WANG Xingzhong1，LI Kang2（1．Ningbo Dahongying University，Ningbo 315175，Zhejiang Province，China；2．Department of Physics，Hangzhou Normal University，Hangzhou311121，China）

Journal of Zhejiang University（Science Edition），2016，43（1）：075－078

Abstract：Firstly，the basic introduction to the distribution function in quantum phase space and the basic properties of non－commutative space and non－commutative phase space were briefly introduced．Then the specific forms of the quantum phase space distribution functions in non－commutative space were also discussed；The specific forms of expression of the static Schr?dinger equation and the energy eigenvalue equation of Wigner function were introduced in commutative space and non－commutative phase space；The evolution rule of the forms in the three dimension spaces had been clearly proposed by comparison．Finally，the Wigner distribution functions of the harmonic oscillator in three dimensional non－commutative space were given explicitly．The result of the study can be applied to more complex physical systems．

Key Words：non－commutative space－time；phase space distribution functions；Wigner distribution function

作者簡介：王興忠（1966－），男，工程師，碩士，主要從事量子相空間分布函數研究及電化教育工作，E－mail：wangxz665049＠163．com．

基金項目：國家自然科學基金資助項目（11175053，11475051）．

收稿日期：2015－03－23．

DOI：10．3785／j．issn．1008－9497．2016．01．013

中圖分類號：O 411．1

文獻標志碼：A

文章編號：1008－9497（2016）01－075－04