磁懸浮永磁直線電動機控制系統非脆弱魯棒控制的研究

藍益鵬　陳其林　胡學成　劉宇菲

(沈陽工業大學電氣工程學院　沈陽　110870)

?

磁懸浮永磁直線電動機控制系統非脆弱魯棒控制的研究

藍益鵬陳其林胡學成劉宇菲

(沈陽工業大學電氣工程學院沈陽110870)

摘要由于磁懸浮永磁直線電動機控制系統存在參數變化、擾動的不確定性以及控制器參數的攝動，因此對該電動機控制系統提出非脆弱魯棒控制，以實現數控機床磁懸浮永磁直線電動機驅動系統的精密控制。建立包含磁懸浮永磁直線電動機參數攝動和外界干擾的狀態空間模型；基于Riccati不等式，推導出滿足非脆弱魯棒性能指標的H∞控制器的解析表達式；在Matlab環境下對控制系統進行仿真研究，仿真結果表明磁懸浮永磁直線電動機控制系統對參數和擾動的不確定性以及對控制器參數攝動具有魯棒性，實驗結果驗證了該控制方法的有效性。

關鍵詞：磁懸浮永磁直線電動機控制系統非脆弱魯棒控制

0引言

磁懸浮永磁直線電動機是在永磁直線電動機的基礎上設計的特種直線電動機，以實現數控機床伺服系統加工過程中的直接驅動與無摩擦進給。由于取消了中間環節以及處于磁懸浮運行方式，電動機本身更容易受到自身參數變化和外部擾動的影響，即對不確定性的影響更加敏感[1-3]，因此，如何設計控制器來保證電動機的穩定運行顯得尤為重要。

數控機床磁懸浮永磁直線電動機控制系統通常是一個高精度的運動控制系統[4，5]，不僅要求電動機在磁懸浮和直接驅動運行過程中對參數攝動和外界干擾具有良好的抑制作用，為了保證足夠的加工精度和表面粗糙度，對控制器自身參數的攝動也要具有良好的魯棒性[6，7]，即要求整個系統是一個非脆弱魯棒控制系統。

本文提出一種非脆弱魯棒H∞控制方法，建立了包含磁懸浮永磁直線電動機參數攝動和外界干擾的狀態空間模型，推導出非脆弱H∞魯棒控制器的解析表達式。對控制系統進行了仿真研究和部分實驗研究。這對進一步提高數控機床伺服系統的性能具有重要意義。

1磁懸浮永磁直線電動機的狀態空間數學模型

磁懸浮永磁直線電動機進給系統的數學模型可描述為[8]

(1)

式中，Fd為端部效應力；Fl為負載阻力；v為動子線速度；Rs為動子電阻；L為d、q軸電感；Ψf為永磁體基波勵磁磁鏈；np為極對數；Kf為電磁推力系數；uq、iq分別為q軸動子電壓和電流。

令

由于電動機中電樞回路電流引起電阻溫度上升，導致Rs發生變化，并且磁路飽和程度不同，引起電感L發生變化，且永磁體充磁的不均勻性，特別是懸浮高度不同，導致Ψf發生變化。因此需要考慮參數攝動問題的數學模型改寫為

(2)

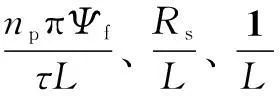
2磁懸浮永磁直線電動機非脆弱魯棒H∞控制的描述

將式(2)簡寫為

(3)

式中，A、B1、B2、C1、D12均為已知矩陣；ΔA、ΔB為參數攝動矩陣，且

[ΔA,ΔB]=EΣ[Fa,Fb]

(4)

式中，E、Fa、Fb均為已知常數矩陣；Σ為未知矩陣，且Σ∈Ω， ΣTΣ≤1。

C1、D12為加權系數矩陣，分別為

考慮控制器攝動針對系統(3)設計的控制器為

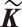
(5)

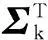
將控制器(5)代入ΔA、ΔB的表達式中，整理得

(6)

式中

Ak=A+B2(K+ΔK), ΔAk=EΣFk

Fk=Fa+Fb(K+ΔK), Ck=C1+D12(K+ΔK)

(7)

從擾動w到評價函數z的傳遞函數為

(8)

3磁懸浮永磁直線電動機非脆弱魯棒H∞控制器的設計

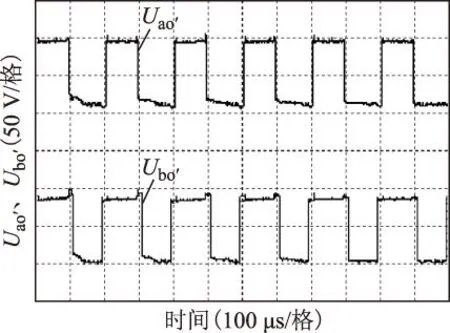
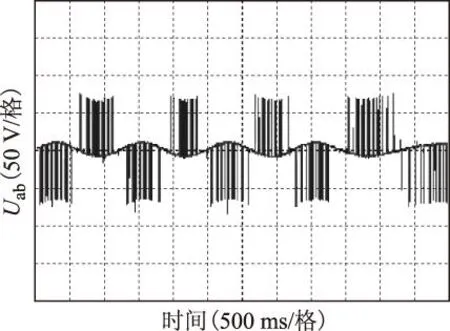
引理1[9]：對于任意矩陣M、N、E和F(FTF

HFE+ETFTHT≤ε-1HHT+εETE

(9)

引理2[10]：對于任意適當維數的矩陣M、N、E和F(FTF>1)，對于任意常數ε>0， 則式(10)成立

(M+HFE)TX-1(M+HFE)<

MT(X-ε-1HHT)M+ε-1EET

(10)

定理：對于給定的被控對象(3)，存在非脆弱狀態反饋控制器式(5)，使得式(8)對于任意的Σ∈Ω都成立的充分必要條件是：對于任意常數ε1、ε2、ε3、ε4均大于0，Riccati不等式為

(11)

存在正定解X，則閉環系統內部穩定，且滿足H∞魯棒性能準則。相應的控制器表達式為

(12)

證明：

1)必要性

由H∞性能指標與Riccati不等式的等價性，存在適當的正定矩陣X使式(13)成立。

(13)

將式(7)代入式(13)得到

X[A+ΔA+(B2+ΔB)(K+ΔK)]+

[A+ΔA+(B2+ΔB)(K+ΔK)]TX+

(14)

整理得

ATX+XA+(B2K)TX+XB2K+X(ΔA+ΔBK)+

(ΔA+ΔBK)TX+XB2ΔK+(B2ΔK)TX+XΔBΔK+

[(C+D12K)+D12ΔK]<0

(15)

考慮引理1和引理2，將式(15)進一步整理得

(16)

(17)

式(17)兩邊同時加上

得到

(18)

式中

(19)

當S=0，控制器K的表達式為

(20)

相應Riccati不等式為

(21)

2)充分性

假設存在任意常數ε1、ε2、ε3、ε4>0，使得Riccati不等式(21)成立且存在正定解X，構造如式(20)的狀態反饋控制器，恒等式

因此不等式

4仿真與實驗結果

4.1磁懸浮永磁直線電動機非脆弱魯棒控制仿真研究

磁懸浮永磁直線電動機的參數：動子質量M=50 kg，動子電阻Rs=1.687 8 Ω，d、q軸電感相等均為L=25.92 mH，極對數np=3，永磁體基波勵磁磁鏈Ψf=0.175 4 Wb，極距τ=33 mm。當懸浮高度在0～2.5 mm之間變化時，對樣機進行實際測試得到參數攝動最大值為：Δ1=7.5%，Δ2=12.5%，Δ3=10%。

取攝動形式的矩陣Σk為

圖1　電流響應曲線Fig.1　Current response curve

圖2　速度響應曲線Fig.2　Speed response curve

圖3　位移響應曲線Fig.3　Displacement response curve

由圖可知，設計的非脆弱的H∞魯棒控制器使閉環系統在0.4 s時達到穩定狀態，且位移無超調。當控制器產生攝動增益時，閉環系統同樣可在0.4 s時趨于穩定，電流響應曲線和速度響應曲線無太大變化，位移響應曲線與攝動前相比基本一致，表明系統對控制器參數變化有魯棒性。

4.2磁懸浮永磁直線電動機非脆弱魯棒控制與PI控制的仿真對比

將非脆弱魯棒控制與PI控制方法進行對比，在0.6 s時突加外部擾動，在0.7 s時卸去擾動，得到電流、速度和位移響應曲線如圖4～圖6所示，圖中1線為非脆弱魯棒控制，2線為PI控制。受到參數攝動的影響，PI控制方法在尚未完全進入穩態的情況下，非脆弱魯棒控制已能較好地實現對系統的控制作用，即對不確定性的影響具有魯棒性。

圖4　電流響應曲線Fig.4　Current response curve

圖5　速度響應曲線Fig.5　Speed response curve

圖6　位移響應曲線Fig.6　Displacement response curve

4.3磁懸浮永磁直線電動機的實驗結果

圖7　磁懸浮永磁直線電動機控制系統Fig.7　The control system of magnetic levitation permanent magnet linear motor

速度參考值對應的標幺值為：Speedref=0.1，對應于0.8 Hz，周期1.25 s，速度52.8 mm/s。直流母線電壓Ud=80 V。此時，對直流中性點o′的相電壓Uao′和Ubo′波形如圖8所示，相電壓只有±Ud/2兩個電平，即+40 V和-40 V。線電壓波形如圖9所示，Uab=Uao′-Ubo′。 Uab線電壓波形有±Ud和0三個電平，即±80 V和0 V，圖9的波形中相對寬的地方是減速反向過程，與理論分析結果一致。空載起動時，用示波器測量電動機的A相電流波形如圖10所示，與電動機動態過程分析一致。

圖8　Uao′、Ubo′相電壓波形Fig.8　Uao′ and Ubo′ phase voltage waveform

圖9　減速反向過程Uab線電壓波形Fig.9　Reverse the process of deceleration Uab line voltage waveform

圖10　A相電流波形Fig.10　A phase current waveform

為測試在非脆弱魯棒控制時系統對參考信號的跟隨性能，在實驗中，速度參考值遇到限位開關時反向，電動機的速度能夠較好地跟隨輸入變化。系統為數字控制系統，采用直線光柵尺測速，速度是經過DSP計算后在虛擬示波器上進行顯示的，其計算過程需要采用標幺值。當速度的標幺值調整為0.08時，對應的速度為42.24 mm/s，采用虛擬示波器測量的v波形如圖11所示，對應的q軸電流波形如圖12所示。圖中，進給系統具有對參考信號的快速跟隨作用，而波形波動明顯，主要是因為動子處于懸浮狀態所引起。通過以上的實驗研究，對該電動機非脆弱魯棒控制的可行性進行了實際驗證。

圖11　速度波形Fig.11　Velocity waveforms

圖12　q軸電流波形Fig.12　Iq current waveforms

5結論

1)針對磁懸浮永磁直線電動機的特殊運行方式，特別是要運行在不同的懸浮高度，存在參數攝動突出的問題，建立了包含磁懸浮永磁直線電動機參數攝動和不確定性擾動的數學模型，進而得到描述系統魯棒控制的狀態空間模型。

2)根據H∞性能指標與Riccati不等式的等價性，推導出參數不確定性的磁懸浮永磁直線電動機控制系統的非脆弱魯棒H∞控制器的解析表達式。

3)在Matlab下，對非脆弱魯棒H∞控制的磁懸浮永磁直線電動機系統進行了仿真研究，該控制器能夠有效抑制電動機參數變化、控制器參數攝動及外部擾動對控制系統的影響。

4)對磁懸浮永磁直線電動機控制系統進行了部分實驗研究。測量了系統的相電壓和線電壓，空載起動時相電流以及速度波形，與理論分析結果基本一致。通過實驗對該電動機磁懸浮運行的可行性進行了實際驗證，為進一步深入研究提供了科學依據。

參考文獻

[1]張魯，寇寶泉，趙斌超，等.新型Halbach次級結構永磁同步直線電機[J].電工技術學報，2013，28(7)：39-45.

Zhang Lu，Kou Baoquan，Zhao Binchao，et al.A novel synchronous permanent magnet linear motor with halbach secondary structure[J].Transactions of China Electrotechnical Society，2013，28(7)：39-45.

[2]陸華才，江明，郭興眾，等.永磁直線同步電機推力波動約束[J].電工技術學報，2012，27(3)：128-132.

Lu Huacai，Jiang Ming，Guo Xingzhong，et al.Thrust ripple suppression for permanent magnet linear synchronous motor[J].Transactions of China Electrotechnical Society，2012，27(3)：128-132.

[3]劉成穎，王昊，張之敬，等.基于非線性電感分析的永磁直線同步電機電磁推力特性研究[J].中國電機工程學報，2011，31(30)：69-76.

Liu Chengying，Wang Hao，Zhang Zhijing，et al.Research on thrust characteristics in permanent magnet linear synchronous motor based on analysis of nonlinear inductance[J].Proceedings of the CSEE，2011，31(30)：69-76.

[4]王昊，張之敬，劉成穎.永磁直線同步電機縱向端部效應補償方法[J].中國電機工程學報，2010，30(36)：46-52.Wang Hao，Zhang Zhijing，Liu Chengying.Compensation methods of longitudinal end in permanent-magnet linear synchronous motor[J].Proceedings of the CSEE，2010，30(36)：46-52.

[5]閆光亞，艾武，陳冰，等.永磁直線同步電機ADRC控制系統[J].電工技術學報，2011，26(9)：60-66.

Yan Guangya，Ai Wu，Chen Bing，et al.PMLSM active disturbance rejection control[J].Transactions of China Electrotechnical Society，2011，26(9)：60-66.

[6]陳一秀，王永初.直線伺服系統的魯棒保性能控制研究[J].中國電機工程學報，2006，26(24)：174-178.Chen Yixiu，Wang Yongchu.Study on robust guaranteed cost control for linear motor servo system[J].Proceedings of the CSEE，2006，26(24)：174-178.

[7]申鐵龍.H∞控制理論及應用[M].北京：清華大學出版社，1996.

[8]藍益鵬，劉宇菲.磁懸浮直線電動機H∞魯棒控制器及其蟻群算法優化設計[J].控制理論與應用，2015，32(4)：527-532

Lan Yipeng，Liu Yufei.Maglev linear motor H∞ robust controller design optimization and ant colony optimization algorithm design[J].Control theory and Applications，2015，32(4)：527-532.

[9]Peterson I R，McFarlane D C.Optimal guaranteed cost control of uncertain linear systems[C]//America Control Conference，Chicago，IL：2929-2930.

[10]Li S H，Zhou M M，Yu X H.Design and implementation of sliding mode control method for PMSM speed regulation system[J].IEEE Transactions on Industrial Informatics，2013，4(9)：1879-1891.

藍益鵬男，1962年生，副教授，博士，博士生導師，研究方向為電機及其控制、魯棒控制。

E-mail：lanyipengg@163.com(通信作者)

陳其林男，1990年生，碩士研究生，研究方向為直線電機伺服系統。

E-mail：1172732825@qq.com

Research on Non-Fragile Robust Control for Magnetic Levitation Permanent Magnet Linear Motor Control System

LanYipengChenQilinHuXuechengLiuYufei

(School of Electrical EngineeringShenyang University of TechnologyShenyang110870China)

AbstractIn the magnetic levitation permanent magnet linear motor control system, there are the problems of parameter variation, disturbance uncertainties, and parameter perturbation in controller. Therefore, in order to realize the precise control for the levitation permanent magnet linear motor drive system of computerized numerical control machine tools, the non-fragile robust control is proposed. The state-space model considering magnetic levitation permanent magnet linear motor parameters perturbation and external disturbances is firstly set up. Then, based on Riccati inequality, the analytic expressions of the H∞ controller are derived to meet the non-fragile robust performance. The simulation research is carried out with the Matlab software. Simulation results show that the magnetic levitation permanent magnet linear motor control system has robustness for the parameter and disturbance uncertainties as well as the controller parameter perturbation. The results of the experimental prove the effectiveness of the control method.

Keywords：Magnetic levitation，permanent magnet linear motor，control system，non-fragile robust control

作者簡介

中圖分類號：TM 383

收稿日期2015-09-10改稿日期2015-12-02

國家自然科學基金資助項目(50975181)。