中心型圓錐曲線內(nèi)接三角形外心的一個(gè)性質(zhì)研究

宋汶釗　王海峰

摘 要：本文修正了中心型圓錐曲線內(nèi)接三角形外心的一個(gè)性質(zhì)，提出并解決了三個(gè)問(wèn)題。首先分析了以往錯(cuò)誤推理的原因，接著修正了中心型圓錐曲線三角形外心的一個(gè)性質(zhì)，在此基礎(chǔ)上，探索了具有上述性質(zhì)的中心型圓錐曲線內(nèi)接三角形面積最值的存在性。本文的研究對(duì)于中心型圓錐曲線的教學(xué)有較好的借鑒和指導(dǎo)作用。

關(guān)鍵詞：中心型圓錐曲線；橢圓；雙曲線；內(nèi)接三角形

一、提出問(wèn)題

筆者首先就張敬坤在《數(shù)學(xué)通訊》期刊中的“圓錐曲線內(nèi)接三角形外心的一組性質(zhì)”（以下簡(jiǎn)稱“例文”）進(jìn)行了研究。例文研究了三種圓錐曲線內(nèi)接三角形外心的一個(gè)性質(zhì)，并且基于反證法得到了圓錐曲線內(nèi)接三角形外心的一組結(jié)論：

結(jié)論1：橢圓內(nèi)接三角形外心不會(huì)與其中心重合。

結(jié)論2：雙曲線內(nèi)接三角形外心不會(huì)與其中心重合。

結(jié)論3：拋物線內(nèi)接三角形外心不會(huì)與其焦點(diǎn)重合。

事實(shí)上，經(jīng)由圖形直觀地分析以及嚴(yán)格數(shù)學(xué)論證，我們發(fā)現(xiàn)例文給出的結(jié)論1和結(jié)論2是錯(cuò)誤的，僅有結(jié)論3是正確的。

本文試圖探討有中心的圓錐曲線，如橢圓和雙曲線（以下稱中心型圓錐曲線）的內(nèi)接三角形外心的性質(zhì)。

我們首先以橢圓為例，通過(guò)圖形直觀分析橢圓內(nèi)接三角形外心的特征。

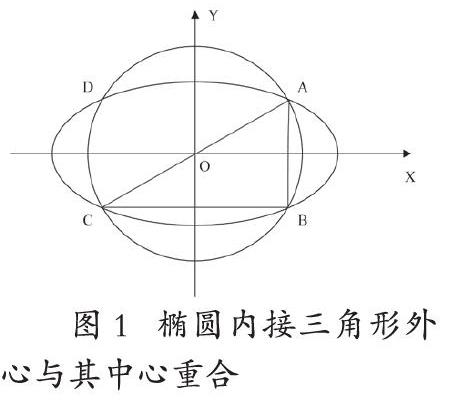
設(shè)橢圓O：（a>b>O），以橢圓中心O為圓心，以半徑a>r>b作圓，則圓O與橢圓必有四個(gè)交點(diǎn)A，B，C，D，則上述任意三個(gè)點(diǎn)組成的橢圓內(nèi)接三角形的外心就是橢圓的中心O，如圖1所示。易知，△ABC為直角三角形，其外心與橢圓的中心重合。

根據(jù)以上事實(shí)，本文提出并探討以下問(wèn)題：

Q1：對(duì)于中心型圓錐曲線，例文看似嚴(yán)密論證的不足之處在哪里？

Q2：中心型圓錐曲線的內(nèi)接三角形外心與其中心是否能夠重合？

Q3：中心型圓錐曲線的內(nèi)接三角形外心與其中心重合時(shí)（下面簡(jiǎn)稱滿足（Q2）），內(nèi)接三角形面積的最大（小）值是否存在？

二、分析問(wèn)題

1.探究例文的問(wèn)題所在

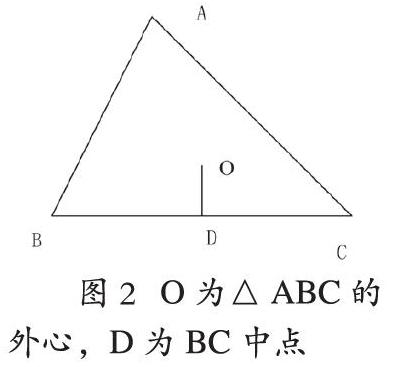
我們仔細(xì)分析例文后，發(fā)現(xiàn)其問(wèn)題所在：例文在推理中用到△ABC的外心O在△ABC各邊的中垂線上，在沒(méi)有仔細(xì)論證的情況下，想當(dāng)然認(rèn)為是圖2中的情形，認(rèn)為OD斜率與BC斜率的乘積為-1。事實(shí)上，由于O點(diǎn)與D點(diǎn)重合，OD的斜率是不存在的。而例文的證明以O(shè)D⊥BC為前提條件，這對(duì)于圖1情形來(lái)說(shuō)，顯然是不妥當(dāng)?shù)摹Ｓ纱耍覀兊玫絾?wèn)題Q1的結(jié)論。

結(jié)論1：例文的論證不足之處在于，使用可能不存在的圖形來(lái)論證，所以得出了錯(cuò)誤的結(jié)論。

由結(jié)論1可得，在探索一個(gè)問(wèn)題時(shí)，僅靠直觀分析是不夠的，還應(yīng)以嚴(yán)格的推理為基礎(chǔ)。

2.探索中心型圓錐曲線的內(nèi)接三角形外心的性質(zhì)

實(shí)際上，上述四組解剛好對(duì)應(yīng)著圖1中的A，B，C，D四個(gè)點(diǎn)。任意取3點(diǎn)可以構(gòu)成一個(gè)三角形，記為△ABC，則此△ABC為直角三角形。根據(jù)直角三角形的性質(zhì)有：斜邊AC的中點(diǎn)就是△ABC的外心，即O（0，0）。

由上面的分析可知，對(duì)于任意一個(gè)橢圓來(lái)說(shuō)，一定存在內(nèi)接三角形，使得該三角形外心與橢圓的中心重合，且該三角形為直角三角形。

需要注意的是，由于b

對(duì)于雙曲線O：（圖3），我們同理可得類似的結(jié)論：

對(duì)于任意一個(gè)雙曲線來(lái)說(shuō)，一定存在內(nèi)接三角形，使得該三角形外心與雙曲線的中心重合，且該三角形為直角三角形。類似可知，該直角三角形的頂點(diǎn)不能落在雙曲線的頂點(diǎn)上。

綜上，我們得到中心型圓錐曲線內(nèi)接三角形外心的性質(zhì)特征：

結(jié)論2：對(duì)于任意一個(gè)中心型圓錐曲線來(lái)說(shuō)，一定存在內(nèi)接三角形，使得該三角形外心與這個(gè)圓錐曲線橢圓的中心重合，且該三角形為直角三角形。

3.探究滿足（Q2）的中心型圓錐曲線內(nèi)接三角形面積最大（小）值是否存在

因此，當(dāng)θ=，時(shí)有S→∞，故不存在最大值；當(dāng)θ→∞，π，2π時(shí)，S→0，故不存在最小值。綜上所述，我們得到下面的結(jié)論：

結(jié)論3：滿足條件（Q2）的中心型圓錐曲線內(nèi)接三角形中，橢圓內(nèi)接三角形面積存在最大值ab，不存在最小值（可以無(wú)限趨于0）；雙曲線內(nèi)接三角形面積不存在最大值（可以趨于無(wú)窮大），也不存在最小值（可以無(wú)限趨于0）。

三、結(jié)論

本文分析中心型圓錐曲線內(nèi)接三角形外心的性質(zhì)，提出并解決了三個(gè)問(wèn)題（Q1，Q2和Q3）。

首先指出例文的錯(cuò)誤在于根據(jù)一個(gè)不存在的圖形進(jìn)行推理（解決了Q1）；其次，我們證明了對(duì)于任意一個(gè)中心型圓錐曲線，一定存在內(nèi)接三角形，使得該三角形外心與這個(gè)圓錐曲線橢圓的中心重合，且該三角形為直角三角形（解決了Q2）；最后，我們證明了滿足條件（Q2）的中心型圓錐曲線內(nèi)接三角形中，橢圓內(nèi)接三角形面積存在最大值ab，不存在最小值（可以無(wú)限趨于0）；雙曲線內(nèi)接三角形面積不存在最大值（可以趨于無(wú)窮大），也不存在最小值（可以無(wú)限趨于0）（解決了Q3）。

本文的研究對(duì)于中心型圓錐曲線的教與學(xué)都具有較好的指導(dǎo)與借鑒意義。

參考文獻(xiàn)：

張敬坤.圓錐曲線內(nèi)接三角形外心的一組性質(zhì)[J].數(shù)學(xué)通訊，2009（20）：30-31.