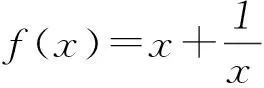歸還權利,創造空間
——數學教學中培養學生數學思級的探索與實踐
?
歸還權利,創造空間
——數學教學中培養學生數學思級的探索與實踐
◇安徽吳亞零
《考試大綱》中指出:“數學思想方法是數學的靈魂、是學生形成良好認知結構的紐帶、是知識轉化為能力的橋梁、是培養學生良好的數學觀念和創新思想的載體,在教學中我們應重視數學思想方法的滲透教學.”從近幾年高考數學試題看,多數題目偏重于運用數學思維解決新問題,“思維容量大”,使得忽視思維訓練的學生得不到高分.因此,數學思維訓練應當引起重視.
本文從數學解題的3個過程(審題、確定解題方法和思想、了解知識點考查的“陷阱點”)出發,闡述如何培養數學思維.
1審題之初:注重“問題導向”構建數學思維
所謂審題,就是弄清楚題目內涵,找已知和未知的關系,并用數學符號表示出來.和審題密切相關的是“問題表現”,即通過審題認識和了解問題的結構,激活與之相關的知識經驗,形成對所要解決問題的一種完整印象.如“二元一次不等式組”的應用.


故在“二元一次不等式組”新授課時應注重引導學生探究“線性規劃”知識可用于解決的問題類型,激發學習興趣.
2解題之中:留足“思考空間”激發數學思維
有的學生只會做講過的題,不會思考新題,缺乏獨立解決問題的能力.課堂教學時應多讓學生講,讓學生思考,留給學生空間.

學生利用函數y=2x與y=lnx在(0,+∞)上無交點,得出“當a>1時函數y=ax與函數y=logax在(0,+∞)上都無交點”.筆者并未指出錯誤,而讓同學們在同一個直角坐標系中畫出2個函數圖象.有的同學結論是沒交點,有的是1個、有的是2個.同學們發現結論不全面.
其中一位同學認為結果可能相交,也可能無交點,與底數a有關.可利用函數f(x)=ax-logax在(0,+∞)的零點個數來確定a的范圍.
筆者肯定了他的結論,又引導他思考y=ax與y=logax互為反函數,于是又有學生指出判斷函數f(x)=ax-x在(0,+∞)上的零點個數即可,y=ax與y=logax是互為反函數,圖象關于y=x對稱.
學生解題過程如下.

當1
f(x)≥f(x0)=ax0-x0=logae-loga(logae).
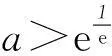
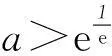
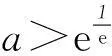
這節課強調學生思考,比直接讓學生判斷零點個數有效.
復習課注重問題設計,一般分為基礎題和綜合題.設計基礎題時要注意以下幾點.
1) 覆蓋課本上最重要和基本知識.
2) 有利于提煉思想方法及檢查學生的概括和應變能力.
3) 問題的設計要新穎,要按邏輯順序編排、由淺入深.盡量設計具有現實意義的問題,能運用一定的思想方法解決的問題.
求參變量的取值范圍.適合采用變式教學,因為當學生產生認知失衡導致緊張感后,為了消除緊張,就會產生認知需要,萌發探索未知的強烈愿望.

分析理解任意和存在這2個邏輯連詞,得出題意是求gmin(x2)≤fmin(x1)+7/2.
變式1若存在x1∈[-1,1],x2∈[1,e],使得g(x2)≤f(x1)+7/2,求實數a的取值范圍.
(gmin(x2)≤fmax(x1)+7/2).
學生嘗試編寫如下變式:
變式2若對任意的x1∈(-1,1], 存在x2∈[1,e],使得g(x2) (gmin(x2) 變式3若對任意x1∈[-1,1], 存在x2∈[1,e],使得g(x2)=f(x1)+7/2,求實數a的取值范圍.(Af?Bg(其中Af與Bg分別為f(x)和g(x)的值域)) 變式4對任意x∈[1,e],使得g(x)≤f(x)+7/2,求實數a的取值范圍.(分離參數法) 同學們通過自己變題并解決問題,并加深了對“求參變量的取值范圍問題”的理解. 3發現“陷阱點”增強學生的數學思維 高三一輪復習重點是夯實基礎,防止解題失誤.學生考試后常感覺題目都做了,得分卻不理想.原因是不清楚命題者的用意.這就要求學生扎實基礎知識,深入理解概念,教師應在上新課時設計好問題串,幫助學生深入理解和掌握所學內容. 例如:“函數的極值”概念的理解. 問題1f(x)=x3在區間(-∞,+∞)上有極大值與極小值嗎? (驗證導函數等于零的根與存在極值點之間的邏輯關系.) (驗證極大值是否一定大于極小值.) 問題3求f(x)=x3-2x2+x在區間[-1,1]上的極值. (驗證區間的端點是否可以為極值點.) 問題4如果函數f(x)的導函數為f′(x)=(x-1)(x-2)(x-3)(x-4),求f(x)極大值點與極小值點. (驗證極大值與極小值的個數是否唯一.) “問題式”概念的理解效果遠大于“說教式”,對概念的詮釋更深刻.也為高三復習做好了鋪墊,再復習這個知識點時學生能有的放矢,了解題目的“陷阱”,減少易錯點. (作者單位:安徽合肥市第六中學) 筆者給出以下變式: