數(shù)學(xué)題的創(chuàng)新解法，貴在反思與領(lǐng)悟

?

數(shù)學(xué)題的創(chuàng)新解法，貴在反思與領(lǐng)悟

◇甘肅吳冠瑛

解題實(shí)踐表明:熟知解題過(guò)程中的一些易錯(cuò)點(diǎn)、失分點(diǎn),有利于將錯(cuò)誤消滅在萌芽狀態(tài),避免走彎路,提高解題的針對(duì)性、實(shí)效性.具體解題中應(yīng)如何有效避錯(cuò)呢？

1要重視對(duì)“基本知識(shí)”的理解

A銳角三角形;B直角三角形;

C鈍角三角形;D以上均有可能

剖析對(duì)向量夾角的概念及銳角三角形的性質(zhì)沒(méi)有理解到位.

反思1) 向量夾角須滿足2個(gè)向量的起點(diǎn)重合(若不重合,可通過(guò)“平移”實(shí)現(xiàn)). 2) △ABC為銳角三角形的充要條件是3個(gè)內(nèi)角都是銳角.

2要重視對(duì)“隱含條件”的深度挖掘

剖析沒(méi)有充分利用一個(gè)三角形為銳角三角形的充要條件.

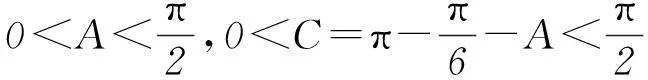
反思1) 本題不但要對(duì)cosA+sinC準(zhǔn)確變形,而且最為關(guān)鍵的是要準(zhǔn)確分析內(nèi)角A的取值范圍. 2) 利用△ABC為銳角三角形的充要條件是不等式0

3要重視對(duì)“聯(lián)系觀點(diǎn)”的理解與運(yùn)用

第(1)問(wèn)通過(guò)求導(dǎo)分析函數(shù)的單調(diào)性,即可求得函數(shù)的最小值.

剖析因放縮過(guò)大導(dǎo)致不能解決目標(biāo)問(wèn)題.

正解(1) 所求最小值為50/27 (具體過(guò)程,略).

又易知0

于是,將上述同向不等式兩邊分別相加得

故得證.

反思本題第(2)問(wèn),大部分同學(xué)沒(méi)有考慮第(1)問(wèn)與第(2)問(wèn)之間的緊密聯(lián)系,即缺乏靈活運(yùn)用“聯(lián)系”的觀點(diǎn)去分析、解決問(wèn)題的思想意識(shí).

(甘肅省教育科學(xué)“十二五”規(guī)劃課題GS[2014]GHB0978)

(作者單位：甘肅靖遠(yuǎn)縣第四中學(xué))