基于技術站改編作業的集裝箱空箱調運魯棒優化

李永軍，段剛，陳莉，田麗娜，蘇旺輝

(1.蘭州城市學院 數學學院，甘肅 蘭州 730070;蘭州交通大學 交通運輸學院，甘肅 蘭州 730070)

?

基于技術站改編作業的集裝箱空箱調運魯棒優化

李永軍1，段剛2，陳莉1，田麗娜1，蘇旺輝1

(1.蘭州城市學院 數學學院，甘肅 蘭州 730070;蘭州交通大學 交通運輸學院，甘肅 蘭州 730070)

摘要:對一般的集裝箱辦理站，考慮到技術站改編時間和運輸走行時間對空箱需求站時間窗的影響，以集結費用、技術站改編費用、車輛走行費用以及空箱早到庫存成本或延誤損失成本之和最小為目標，以車站作業能力和線路通過能力為約束條件，建立基于技術站改編作業的空箱調運模型。針對集裝箱空箱運輸過程中走行時間不確定的特點，建立魯棒軟時間窗組合優化模型。通過等價變換和對偶變換，將魯棒軟時間窗組合優化模型轉換為線性規劃模型，極大地簡化了模型。然后構造基于技術站改編作業的空箱調運魯棒優化模型，并將其轉換為一般的整數線性規劃模型。算例表明，該方法簡單有效。最后對不確定走行時間的個數p進行靈敏度分析，結果表明其存在一個較小的上界。

關鍵詞：鐵路運輸；優化；魯棒軟時間窗；空箱調運；技術站改編作業；不確定走行時間

集裝箱運輸是鐵路貨物運輸發展方向之一。北美的鐵路集裝箱運輸收入早已高居第一，然而我國鐵路集裝箱運輸卻發展緩慢，集裝箱運輸量僅占鐵路貨物發送量的3%。這既有鐵路運能緊張等客觀因素的影響，也受到集裝箱運輸作業組織等方面的制約。科學合理的空箱調運是提高集裝箱周轉率、增加鐵路集裝箱運量和順利完成集裝箱運輸作業組織的重要保證，具有重要意義。Li等[1]對海運業在綠色供應鏈中的責任問題進行了分析，揭示了空箱的合理調運不但可以增加公司利潤，而且還能夠減少供應鏈中的浪費。Song等[2]考慮動態與隨機環境下的空箱配送問題，制定了一個靈活的配送策略：即空箱配送的目的地和數量事先不確定，而是在途中根據港口最新的即時信息來確定。靈敏度分析表明這一策略受貿易不平衡方式、船隊規模和邊界值因素的影響很大，但對需求分布類型和船舶容量并不敏感。Long等[3]通過樣本均值逼近方法求解隨機空箱調運問題，將拉丁超立方設計和過飽和設計相結合，可以得到滿意的逼近結果。通過對一些非獨立同分布數據的計算檢驗表明，該方法不僅適用于隨機空箱調運問題，而且能夠得到高質量的解。閆海峰等[4]建立了結點站間基于徑路選擇的空箱調配優化模型，利用二級耦合反饋系統來設計算法。朱德輝等[5]以運輸費用最小為目標，對罐式集裝箱重箱流和空箱流調配進行了綜合優化。張得志等[6]則分別建立了基于顧客偏好的模糊運輸規劃模型與帶時間窗的運輸規劃模型。段剛等[7]考慮技術站改編作業對空箱調運的影響，建立了基于軟時間窗的鐵路空箱調運優化模型，但卻忽視了走行時間不確定這一重要因素。雖然可以采用隨機規劃的方法建立模型，但求解卻非常復雜。在缺乏統計數據或統計數據不準確時，難以確定隨機變量的概率分布，這時可以采用魯棒優化方法。在已知走行時間變化范圍的情況下，魯棒優化假設這些不確定的走行時間都按照最壞的情況發生。這樣的假設過于保守，因為現實中很少出現所有走行時間都是不確定的情況，即使走行時間都不確定，也不一定都按最壞情況。Bertsimas等[8]放松了這一要求，認為最多有Γ個不確定參數會發生變化，而其余參數都是確定的，取其均值。而且從理論上證明，即使那些確定的參數也發生變化時，原來得到的魯棒解仍會以較大的概率保證其可行性。該方法不但具有很大的靈活性，而且魯棒優化模型與對應的確定型模型具有相同的計算復雜度。本文利用該方法，將走行時間分為確定的和不確定的2類，并只對不確定的時間采用魯棒優化方法。Bertsimas等[8]所建立的模型中，其不確定參數位于約束條件中，而所考慮的不確定的走行時間則位于目標函數中的時間窗里，因此，將其稱為魯棒軟時間窗模型。由于集裝箱中心站或運量較大的辦理站間，其空箱調運大多通過集裝箱班列組織運輸，空箱調運也是以整列直達方式運行。而對大多數二級和三級集裝箱辦理站來說，由于貨源不足且去向不穩定，無法組織專列，空箱調運也只能采取混編形式，這樣就會在前方技術站進行改編中轉作業，從而增加了調運時間，而且只能按指定徑路運輸。在編組計劃確定的條件下，本文對后一種情況進行優化，以集結費用、技術站改編費用、車輛走行費用以及空箱早到庫存成本或延誤損失成本之和最小為目標，以集裝箱辦理站作業能力和線路通過能力為約束，建立了基于技術站改編作業的空箱調運魯棒優化模型。

1時間窗的魯棒優化

1.1基于技術站改編作業和時間窗的集裝箱空箱調運模型

決策變量：xij為表示i站到j站調運的空箱數，(i,j)∈E。

基于技術站改編作業和時間窗的集裝箱空箱調運優化模型如下：

(1)

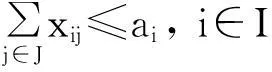
(2)

(3)

(4)

(5)

xij≤rij, (i,j)∈E

(6)

(7)

xij≥0且為整數，(i,j)∈E

(8)

1.2魯棒軟時間窗模型

(9)

(10)

(11)

(12)

其中，式(9)中的βij表示走行時間不確定情況下空箱的最早到達時刻早于時間窗的時間；式(10)中的γij表示走行時間不確定情況下空箱的最晚到達時刻晚于時間窗的時間；式(11)中的ωij表示走行時間確定情況下空箱的最早到達時刻早于時間窗的時間；式(12)中的δij表示走行時間確定情況下空箱的最晚到達時刻晚于時間窗的時間。

由于魯棒軟時間窗模型不僅考慮早到和晚到時間，還考慮了它們的成本，所以也考慮早到和晚到成本。令

λij=max{ujβij,vjγij}, (i,j)∈E

(13)

μij=ujωij+vjδij, (i,j)∈E

(14)

其中，式(13)中的λij表示走行時間不確定情況下空箱的單位早到成本與單位晚到成本的最大值，式(14)中的μij表示走行時間確定情況下空箱的單位早到成本與單位晚到成本之和。

所以，得到魯棒軟時間窗模型：

(15)

2基于技術站改編作業的空箱調運魯棒優化模型及等價變換

2.1基于技術站改編作業的空箱調運魯棒優化模型

將魯棒軟時間窗模型加到式(1)中，替換目標里的早到或晚到成本，就得到基于技術站改編作業的空箱調運魯棒優化模型：

(16)

s.t. yij≥xij, (i,j)∈E

(17)

式(2)-式(8)

式(16)為目標函數，式(17)是對變量yij的限制，其余約束與基于技術站改編作業和時間窗的集裝箱空箱調運模型相同。

2.2魯棒軟時間窗的等價變換

令

(18)

下面給出魯棒軟時間窗R(yij,p)的等價線性規劃形式。

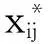
(19)

(20)

0≤zij≤1, (i,j)∈E

(21)

定理1引理1中的線性規劃問題式(19)～(21)的對偶問題為

(22)

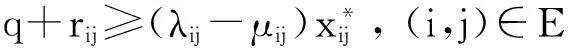
(23)

q≥0

(24)

rij≥0, (i,j)∈E

(25)

證明：顯然

(26)

所以，下述線性規劃問題

(27)

s.t. 式(20)，式(21)

的對偶為

(28)

s.t. 式(23)-式(25)

證畢。

2.3基于技術站改編作業的空箱調運魯棒優化模型的等價形式

定理2基于技術站改編作業的空箱調運魯棒優化模型等價于下面的整數線性規劃模型：

(29)

s.t. 式(2)～式(8)，式(23)～式(25)

定理2的證明見文獻[9]。

由此，將基于技術站改編作業的空箱調運魯棒優化模型轉換為一般的整數線性規劃模型，轉換后的模型與基于技術站改編作業的空箱調運魯棒優化模型相比，僅多了1個連續變量q，且除了非負限制，沒有增加新的約束條件，但將基于技術站改編作業的空箱調運魯棒優化模型目標中的組合優化部分轉換成了線性函數，使之更易于求解。

3算例

某鐵路局有8個空箱供應站，6個空箱需求站，5個技術站。供應站的空箱供應量、出發時間、作業能力和集結費用見表1，需求站的空箱需求量、時間窗、作業能力、早到庫存成本和晚到機會損失如表2所示，供應站與需求站間走行時間范圍及經過的技術站見表3，表4為空箱調運成本和線路間的集裝箱通過能力，表5為技術站改編時間和改編費用。

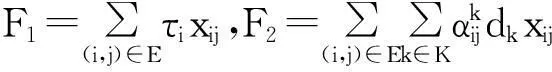
1.2.2 對照組 在基礎疾病治療的基礎上,給予1.25×102 mg美多巴,口服,3次/d。3 w為1療程。

表1　空箱供應站信息

表2　空箱需求站信息

表3供應站與需求站間走行時間范圍(h)及經過的技術站

Table 3 Transportation time and technique station between OD

供應站需求站1234561[7,9]/1[3,7][8,12]/1[5,9][4,6][2,6]2[4,8]/4[7,9]/3[5,9][9,15][3,5][7,8]/33[3,5][5,9][3,7]/5[5,6][2,6]/4[4,8]4[4,6][1,5]/2[5,7]/2[5,8]/1[4,6][8,10]5[9,11]/2[7,8][2,4][3,5][5,7]/4[3,5]/56[3,5][6,8][7,11][6,9][3,4][5,7]/47[2,4]/3[7,14]/2[5,9][3,8]/3[4,10][2,6]8[5,8][5,7][6,8]/5[7,9][4,6]/1[2,5]

注：分子表示走行時間范圍，分母表示經過的技術站。

表4空箱調運成本(元·箱-1)和線路的集裝箱通過能力(箱)
Table 4 Empty container allocation cost and transportation ability between OD

供應站需求站123456140/5060/3020/4030/4070/3030/40270/4040/3020/2030/2050/2090/30320/3070/2090/2060/2030/2040/10430/3020/3070/3030/2040/6060/20510/2040/2060/3020/3030/3020/20690/3030/3070/3040/1060/1090/20760/4050/4040/3020/2030/2090/30830/4060/3020/3060/4090/1070/10

注：分子表示調運成本，分母表示線路的集裝箱通過能力。

表5　技術站改編時間和改編費用

最優解中共有12個xij大于零，即發生了12次空箱調運。由于p= 4，所以只有4個rij取值大于0，分別為r31= 65,r45= 438,r73= 246,r83= 230。由互補松弛定理[10]知，在最優解中，當rij>0時，式(20)中與rij對應的約束條件等式成立，即對應的變量zij=1，也就是說與這4個rij對應的走行時間tij是不確定的。在不確定的走行時間中，供應站3向需求站1調運的空箱，走行時間取其最短時間3 h，6∶00從供應站3出發，因此到達需求站1的時間為9∶00，早于時間窗3 h。其余3個不確定走行時間都取其最大值，因此空箱到達需求站的時間都晚于各自需求站的時間窗。其中，供應站4向需求站5調運的空箱，到達需求站5的時間比時間窗晚2 h；供應站7向需求站3調運的空箱，到達需求站3的時間比時間窗晚6 h；供應站8向需求站3調運的空箱，由于在技術站5進行改編，多消耗了6 h，因此到達需求站3的時間比時間窗晚3 h。

由于在改編站作業會增加運到時間，因此，為滿足時間窗要求，應盡量減少改編作業發生。在最優調運方案中，僅有2次調運發生改編，供應站4向需求站2調運的空箱在改編站2進行改編，供應站8向需求站3調運的空箱在改編站5進行改編，且只有第2個調運發生延誤。共有3條OD路徑的空箱調運量達到了通過能力上限，分別是供應站2到需求站3(20個空箱)，供應站6到需求站2(30個空箱)，供應站8到需求站3(30個空箱)。

p的取值不同時，最優解顯然也會變化，下面p值做靈敏度分析。圖1給出了總成本F，q與p的關系，顯然，總成本F是p的增函數，而q則是p的減函數。但當p= 5時，總成本就不再增加，達到最大值12 910，所以p的上界是5。也就是說，僅有5個不確定走行時間對最優解的影響最大，并使得總成本達到最大。當p≥5時，q= 0。

當p= 0時，所有走行時間都是確定的，此時成本最小，為11 861元，其中F1= 1747，F2= 380，F3= 8 080，F4= 1 654，F5= 0，F6= 0，q= 448。圖2為成本F1,F2,F3,F4,F5,F6隨p的變化情況，可以看出：F2隨p減少；F5隨p增加；F1，F3和F6隨p先增后減；F4則先減后增。

圖1　總成本F和q與p的關系Fig.1 Relationship between total cost F and p

圖2　成本F1, F2, F3, F4, F5和 F6與p的關系Fig.2 Relationship between cost F1, F2, F3, F4, F5 , F6 and p

4結論

1)根據一般集裝箱辦理站適箱貨源少、去向分散、大多要在前方技術站進行改編作業的特點，并考慮走行時間不確定對需求時間窗的影響，建立了基于技術站改編作業的集裝箱空箱調運魯棒優化模型。

2)利用等價變換和對偶變換將空箱調運魯棒優化模型目標中的組合優化部分轉換成了線性函數，轉換后的模型與原來的模型模型相比，僅多了1個連續變量，且沒有增加新的約束條件，因此，極大地簡化了計算難度。

3)算例表明了模型的正確性和有效性。在最優方案中，由于充分考慮到不確定走行時間、空箱改編時間和集結時間的影響，將這些成本降到了最低(共3 158元)，僅占總成本的1/4。且不確定走行時間的個數p的上界僅為6。

參考文獻：

[1] Li Ling, Wang Bin. Enhancing green supply chain initiatives via empty container reuse[J]. Transportation Research Part E, 2014(70):190-204.

[2] Song D P, Dong J X. Effectiveness of an empty container repositioning policy with flexible destination ports[J]. Transport Policy, 2011,18(1):92-101.

[3] Long Y, Chew E P, Lee L H. Sample average approximation under non-i.i.d. sampling for stochastic empty container repositioning problem[J]. OR Spectrum, 2015, 37(2): 389-405.

[4] 閆海峰, 董守清. 鐵路集裝箱結點站間空箱調配的優化[J]. 中國鐵道科學, 2009, 30(1): 131-135.

YAN Haifeng, DONG Shouqing. Optimization of the empty containers distribution among railway network container freight stations[J]. China Railway Science, 2009,30(1): 131-135.

[5] 朱德輝,何世偉.鐵路罐式集裝箱空箱調配優化模型及遺傳模擬退火算法[J].中國鐵道科學, 2008, 29(6): 104-110.

ZHU Dehui, HE Shiwei. Optimization model of railway empty tank container allocation and genetic simulated annealing algorithm[J]. China Railway Science, 2008, 29(6): 104-110.

[6] 張得志, 謝如鶴, 黃孝章. 鐵路集裝箱空箱調度模型及求解算法[J]. 中國鐵道科學, 2003, 24(3): 125-129.

ZHANG Dezhi, XIE Ruhe, HUANG Xiaozhang. Dispatch model and solution algorithm of railway empty container[J]. China Railway Science, 2003,24(3):125-129.

[7] 段剛,李引珍,田麗娜,等.基于技術站中轉作業的集裝箱空箱動態調運優化模型與算法[J].交通運輸系統工程與信息,2012,12(2):111-118.

DUAN Gang, LI Yingzhen, TIAN Lina, et al. Dynamic empty container allocation model and algorithm based on technique station transfer operation[J]. Journal of Transportation Systems Engineering and Information Technology, 2012, 12(2): 111-118.

[8] Bertsimas D, Sim M. The price of robustness[J]. Operations Research, 2004, 52 (1):35-53.

[9] 段剛,陳莉,李引珍，等.基于魯棒軟時間窗的鐵路集裝箱空箱調運優化研究[J]. 鐵道學報,2015,37(9):8-16.

DUAN Gang, CHEN Li, LI Yingzhen, et al. Optimization on railway empty container allocation with robust soft time window[J]. Journal of the China Railway Society, 2015,37(9):8-16.

[10] 李引珍.管理運籌學[M].北京：科學出版社,2012.

LI Yingzhen. Management operations research[M]. Beijing: Science Press, 2012.

(編輯陽麗霞)

Robust optimization on railway empty container allocation under reclassifying operationLI Yongjun1, DUAN Gang2, CHEN Li1, TIAN Lina1, SU Wanghui1

(1. Department of Mathematics, Lanzhou City University, Lanzhou 730070, China;2. School of Traffic and Transportation, Lanzhou Jiaotong University, Lanzhou 730070, China)

Abstract:Taking the impact of reclassifying time and transport time on the time window of demand into consideration for common container terminal, an empty container allocation model based on reclassifying operation in technique station is proposed for minimizing the sum of reclassifying cost, transport cost, accumulation cost and inventory cost for early arriving or loss cost for delaying and subjects to container operating ability and routing transport ability, According to the uncertain transport time, a robust soft time window model of combinatorial optimization is proposed. Equivalent transformation and dual transformation methods were used to simplify the robust soft time window model to a linear programming one A robust optimization of empty container allocation with reclassifying operation in technique station was constructed for transforming it to integer linear programming model. A numerical example demonstrates that the model is simple and effective for improving the efficiency of railway container transportation.

Key words:railway transportation; optimization; robust soft time window; empty container allocation; reclassifying operation; uncertain transportation time

中圖分類號：U292; U294

文獻標志碼：A

文章編號：1672-7029(2016)03-0583-07

通訊作者：段剛(1977-)，男，吉林吉林人，副教授，博士，從事交通運輸系統分析研究；E-mail：dg_77@163.com

基金項目：國家自然科學基金資助項目(11261027，61364026)；甘肅省財政廳基本科研業務費資助項目(213060)；蘭州交通大學青年科學研究基金資助項目(2011020)；蘭州城市學院校長科研創新基金資助項目(LZCU-XZ2014-05)

收稿日期：2015-08-06