改進的雙變量收縮函數模型腦電信號消噪方法*

陳順飛，羅志增，周鎮定

（杭州電子科技大學智能控制與機器人研究所，杭州310018）

?

改進的雙變量收縮函數模型腦電信號消噪方法*

陳順飛，羅志增*，周鎮定

（杭州電子科技大學智能控制與機器人研究所，杭州310018）

摘要：針對傳統小波消噪全局閾值處理獨立性假設和雙變量函數模型對沒有父系數的最高層小波系數不做處理的缺陷，提出一種高密度離散小波變換中利用雙變量收縮函數對腦電信號進行消噪的方法。子小波系數根據雙變量函數實現局部自適應收縮處理。同時根據父系數趨于0時，閾值函數近似于軟閾值函數，對最高尺度小波系數進行軟閾值法消噪。從實際信號處理效果和客觀定量指標兩方面進行評價，結果表明這種改進算法都優于軟閾值法、硬閾值法以及雙變量收縮法。

關鍵詞：腦電信號；信號消噪；高密度小波變換；雙變量收縮函數

腦電信號EEG（Electroencephalogram）是由頭皮表面大量神經元突觸后電位同步綜合而形成的，反映大腦運行狀態和神經細胞活動情況的生物電信號。因此，對于腦電信號的分析可以獲得大量的生理、心理及病理信號［1-2］。腦電信號是一種非平穩非線性極其微弱的隨機信號，其幅值是μV級，極易受到噪聲干擾，如工頻干擾、靜電干擾、眼電偽跡、心電偽跡等［3-4］。去除腦電信號中的噪聲信號，提升腦電信號的信噪比是腦電信號處理中的首要環節。小波變換由于其具有良好的時頻局部化特性、多分辨率特性、解相關性、選基靈活性［5］等特點，在生物醫學信號消噪領域中得到廣泛應用［6］。小波閾值消噪法［7］將信號通過小波分解轉化為一系列的分解系數，對不同尺度下的小波系數作閾值收縮處理，可以起到消噪作用。常用的閾值消噪方法有：軟閾值法［8］、硬閾值法［9］等。傳統的小波閾值消噪方法都假定不同尺度上的小波系數之間是相互獨立的，忽視了父小波系數與子小波系數之間的強相關性［10］。信號與噪聲的小波變換在各尺度下的不同傳播特性表明，父系數與子系數之間的強相關性恰恰是普遍存在的。因此基于獨立性假設的閾值消噪算法將導致原本相關的信息被重復處理，使信號消噪過程中丟失一些重要的細節特征，不利于信號奇異點的檢測，且易出現偽吉布斯現象，給進一步分析帶來誤差［11］。針對傳統小波閾值消噪方法的不足，本文提出一種改進的雙變量收縮函數模型消噪方法。在高密度離散小波變換出色的信號特征表達能力的基礎上，結合雙變量收縮函數［12-14］具有考慮父小波系數與子小波系數之間強相關性的特性，實現小波系數閾值的局部自適應收縮處理，避免了由于獨立性假設導致的重復處理。考慮到傳統的雙變量收縮函數模型缺乏對最高層小波系數的處理，而最高層小波系數雖然處于較低頻帶，但同樣含有噪聲［15］。本文提出的方法將對最高層小波系數采用軟閾值法進行閾值處理。改進算法在腦電信號消噪處理實驗應用中取得了較好的消噪效果。

1　雙變量收縮函數

假設腦電信號是被方差為σ2n的加性高斯白噪聲所污染，則有：

式（1）中，n為高斯白噪聲，x為腦電信號。消噪的目的就是要從含噪信號s中估計出腦電信號x，將含噪信號s由時域變換到小波域，分解得到多尺度的小波系數，如式（2）。

式（2）中的y代表含噪信號的小波系數，w為腦電信號所對應的小波系數，n為噪聲的小波系數。由于雙變量收縮函數需考慮小波系數及其父系數的相關性，故設w1k表示第k層的小波系數，w2k表示下一層中與w1k位置相對應的父節點小波系數，可得向量表示為：

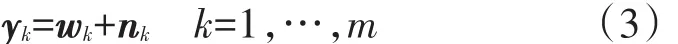
其中yk=（y1k，y2k），wk=（w1k，w2k），nk=（n1k，n2k），m為子小波系數的數目。采用最大后驗概率公式估計未受噪聲污染的信號的小波系數w^ (yk)，記為式（4）。

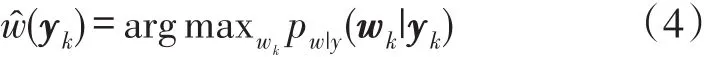
由貝葉斯概率估計作進一步推導之后，可將式（4）轉換為式（5）。

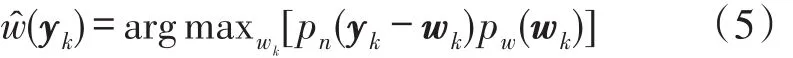
由式（5）可知，只有分別求得噪聲系數的概率密度函數pn（n）和目的信號系數的概率密度函數pw（wk），才可得到真實信號的系數估計(yk)。假設各層噪聲信號n1k，n2k為獨立同分布的高斯變量，因此n的概率密度函數pn（n）可表示為：

而不同尺度下小波系數的概率密度函數pw（wk）可表示為［12］：

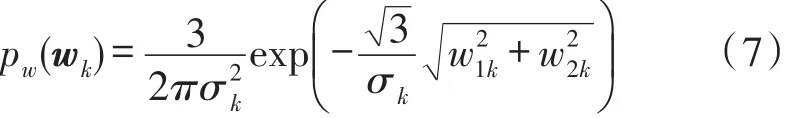
其中(g)+={0 g＜0 g g≥0。式（8）表明真實信號第k層小波系數的估計值不僅與子小波系數y1k有關，還與父小波系數y2k、第k層的信號方差σ2k和噪聲信號方差σ2n有關，使系數收縮處理具有較強的局部自適應能力。當父系數較大時，小波系數估計值的收縮比例較小，而當父系數趨于零時，公式計算得到的閾值函數就近似于軟閾值函數。估計值的雙變量收縮閾值函數如圖1所示。結合式（8）與圖1的結果表明，當含噪子小波系數和含噪父小波系數的平方和小于閾值時，估計值為0。由于小波變換后較小的小波系數中含有多數噪聲，因此雙變量收縮閾值處理可以有效的濾除噪聲。同時，圖1中子小波系數的估計值小于相對應的含噪子小波系數y1k，實現了小波系數的收縮變換。傳統的雙變量收縮函數模型對于沒有父系數的最高層小波系數不做任何處理，最高層小波系數雖然處于較低頻段，但是同樣含有噪聲［15］。從上述的分析中得知，當父系數趨于零時，閾值函數類似于軟閾值函數。因此本文提出的算法模型在雙變量函數模型的基礎上，增加對最高層小波系數的軟閾值處理。

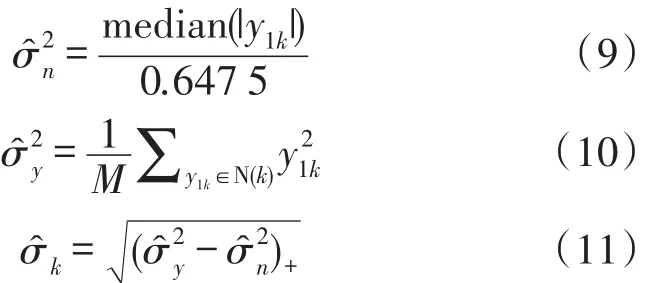
圖1　?的雙變量收縮函數圖

2　高密度離散小波變換

高密度離散小波變換HDDWT（High Density Discrete Wavelet Transform）［16-17］是一種改進的小波變換，相比于一代小波分析，它具有近似的平移不變的特性，更出色的信號表達能力，能夠在時頻域上更加細致地刻畫信號，擁有更佳的信號降噪性能。

農業始終是我國重要的產業之一，我國人民就沒有放松對農業生產技術的追求和鉆研，近些年，規模化、現代化、產業化的農業已經逐漸代替傳統農業生產方式，科學技術對于農業生產的重要性日益顯著。玉米作為我國重要的糧食作物和經濟作物，相較水稻和小麥，玉米在耐旱等方面更具優勢，山區氣候和地質條件對玉米的產量和質量有更高的需求，我國近些年一直在研究山區玉米高產栽培技術，并進行推廣應用。

HDDWT最大特點是具備間尺度分析的特性，即第二個母小波是按1/2的倍數進行平移，這使得HDDWT在時頻域上的采樣密度為非冗余小波變換的三倍。基于高時頻采樣密度的HDDWT在降低對信號平移敏感性的同時獲得了出色的時頻域分辨能力。HDDWT對信號進行分解重構示意圖如圖2所示。它由三個通道濾波器組來實現。圖2中hi（n）（i=0，1，2）分別表示小波的低通濾波器、帶通濾波器和高通濾波器。

圖2　HD-DWT對信號進行分解重構示意圖

HDDWT尺度系數與小波系數分別由式（12）～式（14）計算得到

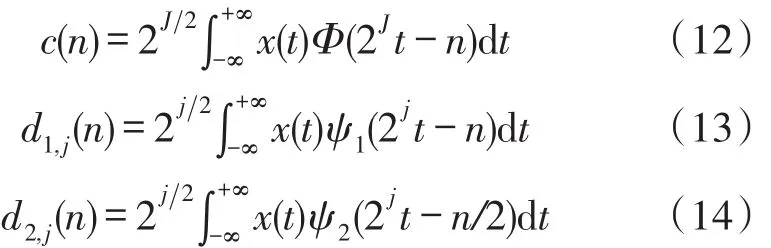
其中，di，j（n）表示第j級分解后得到的第i個小波系數。同時HDDWT的尺度函數與兩個母小波函數需分別滿足以下的約束關系。

式中，Φ（t）為基函數，ψ1(t)、ψ2(t)分別代表兩個小波函數，值得注意的是ψ2(t)是以1/2的整數倍作平移的。根據多采樣率信號處理的關系，HDDWT若要實現重構需滿足表達式（18）和式（19）。

其中Hi（z）為hi（n）（i=0，1，2）的z變換，其中H2（z）可通過H0（z）和H1（z）因式分解得到。如果達到上述重建條件，且Φ（t）足夠正則，則信號重構的表達式為：

本文基于雙變量收縮函數的局部自適應能力和高密度離散小波變換出色的信號描述能力，對腦電信號進行消噪分析。具體算法實現步驟如下：

Step 2對任意的一列小波系數y1k找到其對應的父系數y2k。

Step 3根據公式（8）求得對應小波系數收縮后的估計值，并以代替原始的小波系數，完成消噪處理。同時對最高尺度的小波系數進行軟閾值法消噪處理。

Step 4對各尺度的系數自下而上進行重構，即可得到消噪后的腦電信號。

3　實驗結果分析

3.1實驗設計與結果

本文應用美國NeuroScan公司的scan4.3腦電采集系統對腦電信號進行采集實驗，設備采樣頻率為250 Hz，精度為32 bit，并選擇陷波濾波濾除50 Hz工頻干擾。本實驗以3位身體健康的在校男性研究生作為受試者，在受試者意識清醒的情況下進行腦電實驗。腦電電極按照國際標準導聯10/20系統放置，以左側乳突和右側乳突為參考電極。本文選擇典型樣本C3通道進行腦電信號消噪實驗分析。本實驗通過采集想象左手、右手、雙腳、舌頭所產生的腦電信號進行消噪處理。每次實驗的持續時長為9 s：0～2 s，受試者處于想象運動準備狀態；2 s時，系統發出“叮”提示音，提示受試者集中注意力；3 s～6 s時，受試者根據屏幕上出現上（↑）、下（↓）、左（←）、右（→）四個方向的誘導圖片分別想象雙腳腳趾前曲、舌頭后卷、左手揮動和右手揮動這4種運動，直至第6 s時系統發出“嘟”的提示音，受試者結束想象，放松調整。一次完整實驗的采樣時序如圖3所示。完成4種想象運動實驗各采集4組腦電數據，每組進行10次實驗，總共160次實驗數據。

圖3　實驗設計流程時序圖

選取一組實驗中C3通道運動想象部分（第3 s～7 s）的腦電信號波形進行消噪處理。因為db小波函數在時頻域上都有較好的局域性，所以選擇db5作為小波分解的母小波進行對比實驗分析。實驗通過多次對比發現，當小波分解的層數為3層時，信號消噪效果較好。將原始信號分別經過小波軟閾值、小波硬閾值以及改進的BSF-HDDWT法進行消噪效果對比分析，分析結果如圖4所示。從圖4可以看出三種算法都取得一定的消噪效果。雖然經前兩者算法處理后的信號噪聲得到了明顯的消除，但原始腦電信號中一些細節信息與邊緣特征亦被過濾，出現過平滑的現象。而采用改進的BSF-HDDWT方法消噪后的腦電信號波形相對清晰，更重要的是原始信號的細節特征也被很好地保留下來。

為了定量分析改進算法的優越性，利用兩個常用的去噪指標均方根誤差RMSE與信噪比SNR來評價信號的消噪效果。對160次實驗數據求得3種消噪算法的RMSE和SNR，并取均值和標準差如表1所示。根據RMSE與SNR的評判標準可知，RMSE的值越小，SNR的值越大表示信號的消噪效果越好。從表1可以看出，改進的BSF-HDDWT法在SNR和RMSE方面都得到較好的提高，從定量上說明改進的BSF-HDDWT算法優于其他2種算法。

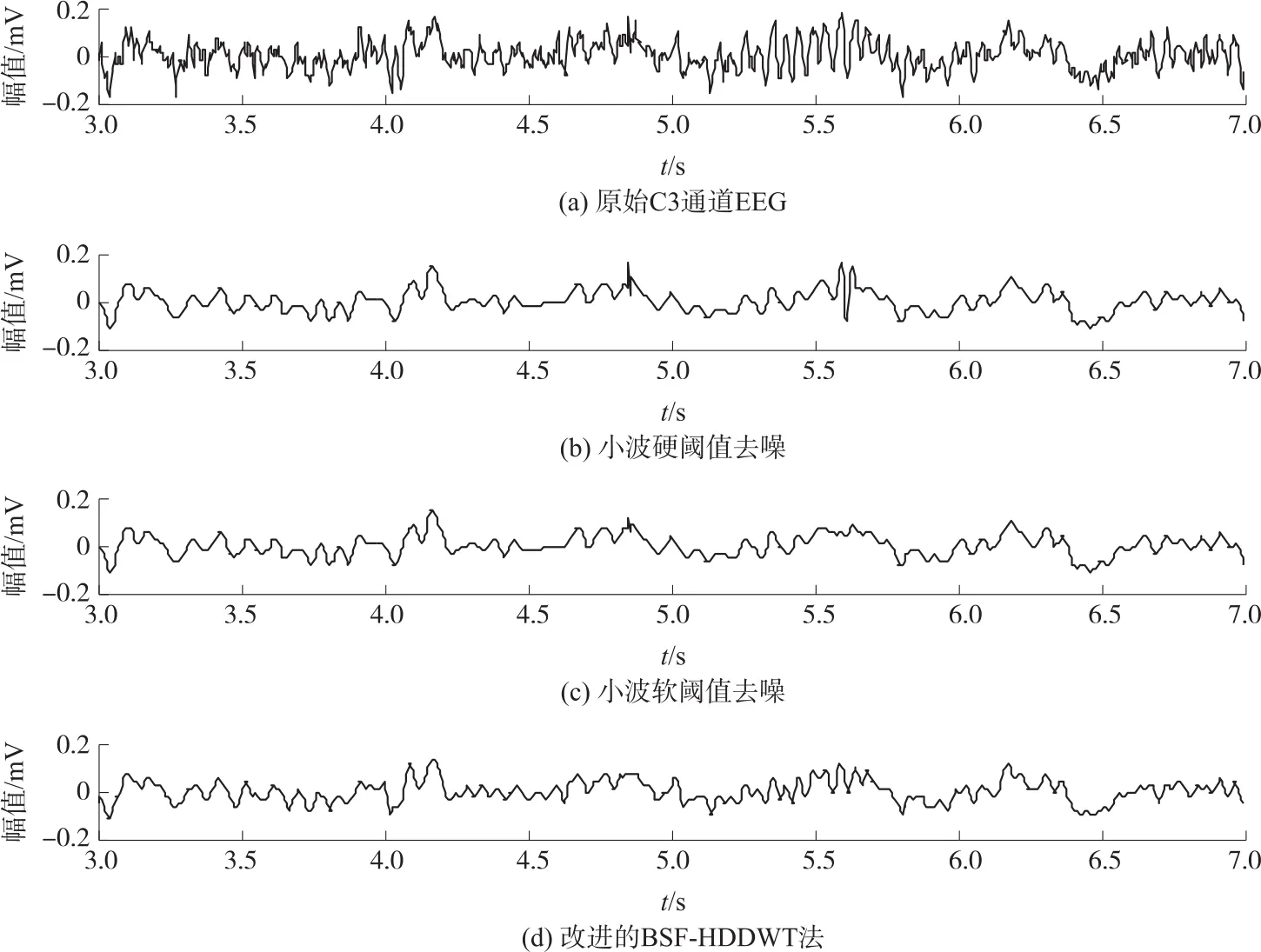
圖4　多種消噪方法消噪效果對比圖

表1　3種消噪算法的RMSE和SNR結果對比

3.2仿真實驗與結果分析

為進一步驗證改進BSF-HDDWT算法的消噪效果，用Matlab構造一個采樣頻率為250 Hz，采集時長為6 s的仿真信號S（t），如式（21）所示。

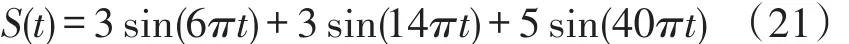
在仿真信號中添加信噪比為5的高斯白噪聲，對混合后的信號利用軟閾值法、BSF-HDDWT法、以及改進的BSF-HDDWT法進行消噪分析，對消噪后的信號進行傅里葉變換轉化到頻域如圖5所示。從圖5中可以看出，軟閾值法雖然濾除了大部分噪聲，但是由于軟閾值法閾值選取的全局性缺陷，忽略小波系數層與層之間的相關性，造成對細節信號多次重復處理，使得仿真中的高頻成份40 Hz的信號被嚴重削弱，這會造成信號的失真現象嚴重。BSF-HDDWT法相比于軟閾值法在細節保持方面得到明顯改善，從圖中可以看出信號的三個峰值，但是由于該方法沒有對最高層的小波系數進行處理，因此在低頻信號存在較多的噪聲，如14 Hz～40 Hz之間的噪聲較多，而在實際腦電信號分析中，14 Hz～40 Hz頻率段含有豐富的腦電信號特征。而本文對BSF-HDDWT的改進算法，相比于前兩者，既可以保留更多的細節信號，又可以濾除最高層小波系數中的低頻噪聲信號。

對信噪比為1、5、10加噪后的信號進行分析，用小波軟閾值法、小波硬閾值法、小波BSF法、BSFHDDWT法、改進的BSF-HDDWT法分別進行消噪處理，評價結果如表2所示。

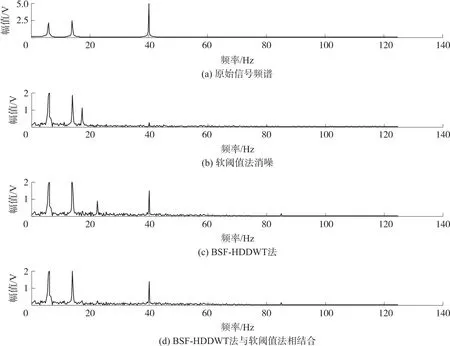
圖5　多種消噪方法的消噪效果頻域對比圖

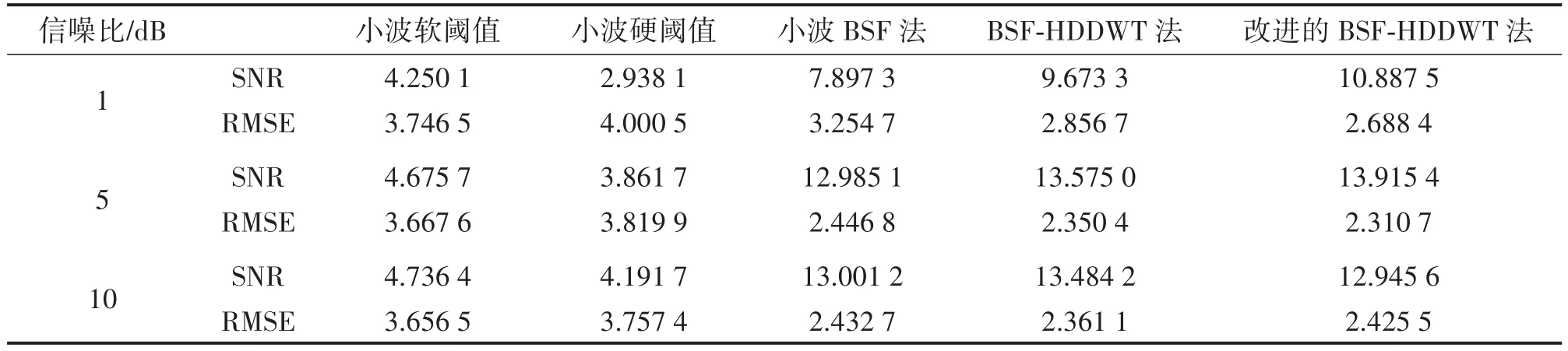
表2　5種消噪方法的去噪評價結果對比

結合圖5和表2，小波軟閾值法和硬閾值法由于全局性的閾值處理，使得幅值為5 V，頻率為40 Hz的信號分量被嚴重削弱，因此SNR和RMSE的評價效果較差。而以雙變量收縮函數為基礎的3種算法的消噪結果則明顯優于上述兩種方法。雙變量收縮閾值函數利用各層小波系數的局部方差對消噪閾值大小進行調整，同時考慮父系數與子系數之間的強相關性對小波系數作收縮處理，使小波閾值消噪具有局部自適應的能力，進而更好的保留信號的細節特征。從表2中可以看出，相比于一代離散小波，具備近似平移不變特點的HDDWT能更細致地刻畫信號的時頻域特點，使處理之后的信號更接近于目標信號的真實波形特征，具有更佳地信號消噪能力。對比BSF-HD?DWT法與改進的BSF-HDDWT法的SNR和RMSE評價結果，當信噪比為1和5時，由于噪聲干擾較強，改進的BSF-HDDWT法能夠改善對最高層小波系數的閾值消噪處理，因此具有相對BSF-HDDWT法較好的消噪效果。而當信噪比為10時，BSF-HDDWT法的消噪效果則優于改進算法，這是因為此時噪聲干擾較小，改進的BSF-HDDWT法會對信號進行過度處理，導致消噪效果變差。從中可以得出結論，本文改進的BSF-HDDWT法比較適合頻帶復雜的強噪聲信號的消噪處理。由于實驗采集到的腦電信號是一種極其微弱且噪聲較強的信號，因此可以采用本文改進的BSF-HDDWT法對其進行消噪處理。

4　結論

本文針對腦電信號微弱且頻域特征復雜、噪聲干擾強的特點，引入對不同尺度的小波系數有局部自適應能力，能有效刻畫信號細節特征的雙變量收縮閾值函數，并結合擁有出色信號表達能力的高密度離散小波變換對腦電信號進行消噪處理。同時對含有低頻噪聲的最高尺度小波系數進行軟閾值法消噪處理。利用多種消噪方法進行實驗對比分析，通過實際信號與仿真信號的處理效果觀察和SNR、RMSE客觀指標進行評價，實驗結果表明，本文改進的BSF-HDDWT法具有更強的噪聲抑制能力，同時可以更好地保留信號的細節特征。良好的消噪效果和保留信號細節的能力，為后續腦電信號的特征提取與和模式識別打下堅實的基礎。

參考文獻：

［1］馬玉良，許明珍，佘青山，等.基于自適應閾值的腦電信號去噪方法［J］.傳感技術學報，2014，27（10）：1368-1372.

［2］Mporas I，Tsirka V，Zacharaki E I，et al.Seizure Detection Using EEG and ECG Signals for Computer-Based Monitoring，Analysis and Management of Epileptic Patients［J］.Expert Systems with Applications，2015，42（6）：3227-3233.

［3］王兵，王魁，梁曉霖，等.腦電信號中工頻干擾去除的綜合研究［J］.傳感技術學報，2010，23（1）：87-92.

［4］吳明權，李海峰，馬琳.單通道腦電信號中眼電干擾的自動分離方法［J］.電子與信息學報，2015，37（2）：367-372.

［5］潘泉，孟晉麗，張磊，等.小波濾波方法及應用［J］.電子與信息學報，2007，29（1）：236-242.

［6］羅志增，周鎮定，周瑛，等.雙樹復小波特征在運動想象腦電識別中的應用［J］.傳感技術學報，2014，27（5）：575-580.

［7］吳光文，王昌明，包建東，等.基于自適應閾值函數的小波閾值去噪方法［J］.電子與信息學報，2014，36（6）：1340-1347.

［8］Donoho D L.De-Noising by Soft-Thresholding［J］.IEEE Transac?tions on Information Theory，1995，41（3）：613-627.

［9］Zhang X，Feng X，Wang W，et al.Image Denoising via 2D Diction?ary Learning and Adaptive Hard Thresholding［J］.Pattern Recog?nition Letters，2013，34（16）：2110-2117.

［10］Simoncelli E P.Bayesian Denoising of Visual Images in the Wave?let Domain［M］.New York：Springer，1999：291-308.

［11］Cho D，Bui T D.Multivariate Statistical Modeling for Image De?noising Using Wavelet Transforms［J］.Signal Processing：Image Communication，2005，20（1）：77-89.

［12］Sendur L，Selesnick I W.Bivariate Shrinkage Functions for Wave?let-Based Denoising Exploiting Interscale Dependency［J］.IEEE Transactions on Signal Processing，2002，50（11）：2744-2756.

［13］Min D，Jiuwen Z，Yide M.Image Denoising via Bivariate Shrink?age Function Based on a New Structure of Dual Contourlet Trans?form［J］.Signal Processing，2015，109：25-37.

［14］Sethunadh R，Thomas T.Spatially Adaptive Image Denoising Us?ing Inter-Scale Dependence in Directionlet Domain［J］.IET Im?age Processing，2014，9（2）：142-152.

［15］李向軍，姜玉莉.一種改進的雙變量收縮模型圖像去噪［J］.現代電子技術，2014（8）：132-134，137.

［16］Qin Y，Tang B，Wang J.Higher-Density Dyadic Wavelet Trans?form and Its Application［J］.Mechanical Systems and Signal Pro?cessing，2010，24（3）：823-834.

［17］Selesnick I W.A Higher Density Discrete Wavelet Transform［J］.IEEE Transactions on Signal Processing，2006，54（8）：3039-3048.

陳順飛（1992-），男，浙江麗水人，碩士研究生，研究方向為生物醫學信息檢測、信息融合與信息處理，142060149@hdu.edu.cn；

周鎮定（1989-），男，碩士研究生，研究方向為生物醫學信息檢測、信息融合與信息處理。

羅志增（1965-），男，浙江慈溪人，博士生導師，1998年在浙江大學獲博士學位，主要從事智能機器人技術、傳感器及多信息融合、生物醫學信息檢測與利用等領域的研究，luo@hdu.edu.cn；

EEG Denoising Method Based on Improved Bivariate Shrinkage Function*

CHEN Shunfei，LUO Zhizeng*，ZHOU Zhending
（Robot and Intelligent Control Research Institute，Hangzhou Dianzi University，Hangzhou 310018，China）

Abstract：Traditional wavelet denoising methods have an assumption that the wavelet coefficients are independent in global thresholding.Then traditional bivariate shrinkage function model has a deficient in not considering the highest scale wavelet coefficients with no parents coefficients.To tackle these defects，in this paper an EEG denois?ing method is proposed based on high density discrete wavelet transform using bivariate shrinkage function.In this method，the children coefficients will achieve local and adaptive shrinking treatment using bivariate function.Then because of the appearance when the parents coefficients tend to zero，the threshold function approximate to the soft threshold，the soft threshold is used for denoising in the highest scale wavelet coefficients.The results show that this improved method is better than the soft threshold，the hard threshold method and bivariate shrinkage method from two perspectives，the actual signal processing effect and the objective quantitative indicators.

Key words：EEG signal；signal denoising；high density discrete wavelet transform；bivariate shrinkage function

doi：EEACC：523010.3969/j.issn.1004-1699.2016.02.016

收稿日期：2015-08-27修改日期：2015-10-14

中圖分類號：TP391

文獻標識碼：A

文章編號：1004-1699（2016）02-0242-06

項目來源：國際自然科學基金項目（61172134，61201302）