基于CE/SE方法模擬空氣中RDX-Al懸浮粉塵的兩相爆轟*

昝文濤,洪 滔,董賀飛

(1.北京理工大學,北京 100081;2.北京應用物理與計算數學研究所,北京 100094)

基于CE/SE方法模擬空氣中RDX-Al懸浮粉塵的兩相爆轟*

昝文濤1,2,洪 滔2,董賀飛2

(1.北京理工大學,北京 100081;2.北京應用物理與計算數學研究所,北京 100094)

通過CE/SE方法模擬了空氣中炸藥-鋁粉塵的兩相爆轟過程,研究了雙粉塵爆轟過程中粒子不同密度對爆轟波速度、壓力的影響,得到密度與波速、爆壓間的線性關系。模擬得到懸浮粉塵在復雜通道中的爆轟波傳播過程,研究了雙粉塵爆轟的流場演化過程,選取流場中的一些點對該處流場的壓力及溫度隨時間的變化進行重點研究,對比了單鋁粉塵在同種條件下的爆轟過程,發現雙粉塵爆轟明顯提高了爆轟波波速和流場的壓力及溫度。模擬結果表明CE/SE方法可以成功模擬雙粉塵的爆轟過程,可為多粉塵爆轟的研究提供參考。

爆炸力學；粉塵爆轟；CE/SE；懸浮炸藥-鋁粉塵

溫壓彈作為一種非常規武器,具有耐高溫高壓、作用時間長、作用范圍廣等優點。在對固體云爆劑的研究中,鋁作為一種質輕含能高的金屬被廣泛采用,因此對于炸藥粉塵鋁粉塵等多種粉塵形成的兩相爆轟過程發展及傳播的研究具有極其重要的意義。含鋁復合裝藥具有爆溫爆壓高、作用范圍廣的優點[1]；陳朗等[2]研究了鋁粉塵尺寸對于爆炸性能的影響,發現了小尺寸粉塵作用時間短放能快；洪滔等[3]數值模擬了炸藥顆粒與鋁顆粒混合粉塵的雙波陣面爆轟,分析對比了雙顆粒與單顆粒爆轟的爆轟波參數。

爆轟模擬過程中最重要的是捕捉強間斷問題,近些年發展出了一系列的格式方法,例如TVD格式、ENO格式、WENO格式、BGK格式和RKDG格式等。CE/SE(時-空守恒元解元)方法是一種解雙曲守恒方程的新方法,它在概念和方法上都不同于已有的方法[4],將時間和空間作為一個整體統一對待,使得從整體和局部都滿足守恒律。Y.Wu等[5]將這種方法拓展應用到化學反應流。董賀飛等[6]應用CE/SE方法模擬了RDX顆粒在空氣中的爆轟問題。

本文中應用CE/SE方法并采用兩相流模型,分析顆粒不同密度對爆轟速度的影響,并研究RDX顆粒和鋁顆粒懸浮粉塵在復雜通道中的爆轟過程。

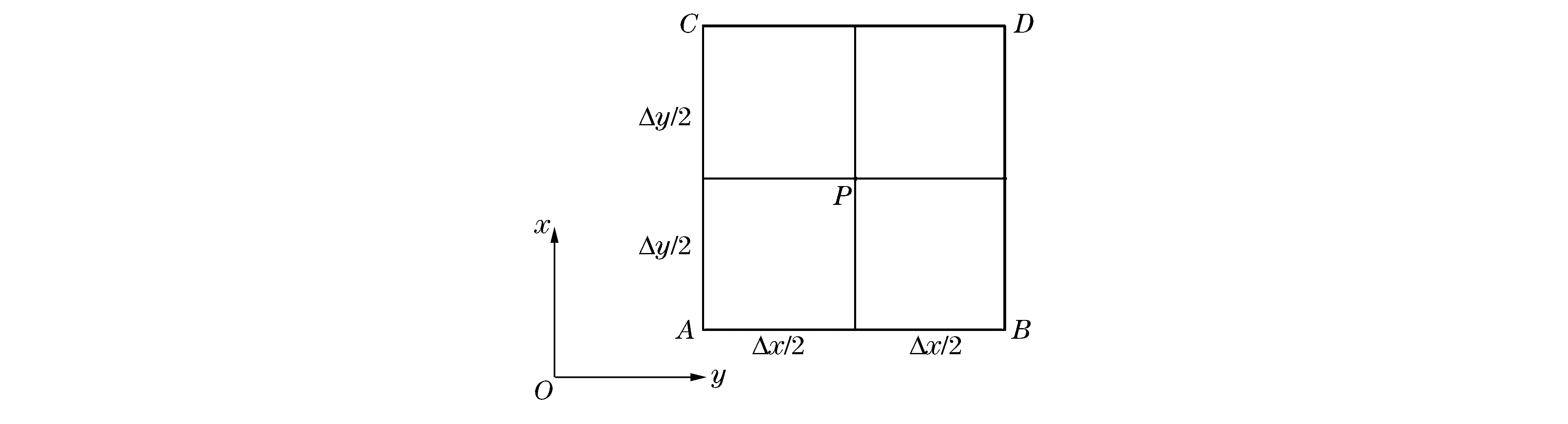
圖1 CE/SE求解區域模型Fig.1 CE/SE area model

1 數值方法及爆轟模型

時-空守恒元解元方法[4,7-8]與傳統差分方法相比,具有構造簡單、格式精度高、分辨率較高等特點。對于二維守恒方程組：

(1)

(2)

式中：

(3)

(4)

(5)

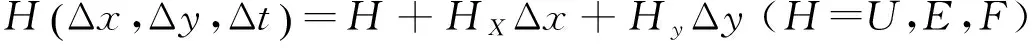
物理量偏導數為:

(6)

式中：I=x,y;α=1～2;U-I,U+I為在相應方向上的左右導數,對其采用中心差分。然后帶入方程得到其他物理量導數。

(7)

(8)

(9)

(10)

采用CE/SE方法求解不含源項歐拉方程,對歐拉方程中的源項采用4階龍格庫塔方法求解。

模擬過程采用了兩相流模型,假設顆粒為球形,初始直徑都相同,顆粒的溫度都是均衡的,忽略了粒子間的作用,粒子化學反應產生的能量假定都被氣體吸收,氣體的組分都是均勻的,略了粒子和墻壁間的熱傳導,忽略粒子與氣體間的輻射作用,固相和氣相都滿足方程。

氣相方程：

(11)

(12)

(13)

(14)

固相方程：

金融行業與相關市場是一種唇齒相依的關系，比如，沒有證券期指、股票對沖等投資工具，證券投資人就不得不承受市場單邊下行的風險。

(15)

(16)

(17)

(18)

(19)

組分方程：

(20)

氣體狀態方程：

(21)

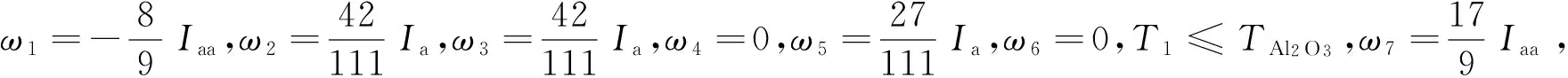
對于RDX炸藥,采用洪滔等[9]提出的模型,計算公式如下：

(22)

式中：Tm為炸藥顆粒的熔點,L為炸藥潛熱。炸藥顆粒在激波作用下運動,并在熱傳導作用下升溫,當到達炸藥顆粒熔點后開始熔化,發生剝離現象,在高溫氣體環境中瞬時分解,釋放能量。

對于鋁顆粒,采用以下模型[10]：

(23)

(24)

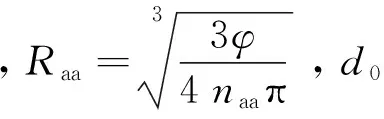
(25)

(26)

式中：Re為雷諾數,Qa為氣體與粒子間的熱傳導,

(27)

式中：λ1為氣體導熱系數,Nu為Nusselt數,q為單位質量的粒子的反應能。

當溫度高于金屬氧化物沸點TAl2O3時,金屬氧化物會發生分解[11],生成氣態Al和O2,因此溫度將保持在金屬氧化物沸點。

2 模擬結果

為了驗證程序的正確性,分別對單獨炸藥顆粒和鋁顆粒情況進行了模擬。炸藥密度為750 g/m3,半徑為20 μm,起爆條件為φ1=1、ρ1=3 kg/m3、u1=1 000 m/s、T1=3 600 K。粉塵從左端起爆,邊界條件為左端封閉,右端開口。得到爆轟波傳播速度約為1.899 km/s,峰值壓力約4.75 MPa。S.Eidelman等[12]得到的峰值壓力為4.84 MPa,D.L.Zhang等[7]在計算中得到的爆轟波傳播速度為1 802 m/s,董賀飛等[13]得到的爆轟波速度為1 916 m/s,鋁粉塵的密度為304 g/m3,鋁顆粒半徑為1.7 μm,爆轟管直徑為15.2 cm。起爆條件為φ1=1、ρ1=3kg/m3、u1=1 000 m/s、T1=3 600 K。從左端起爆,邊界條件為左端閉合,右端開口,上下為固壁。得到的爆轟波參數為D=1 630 m/s、ρCJ=2.43 kg/m3、uCJ=673 m/s、PCJ=2.04 MPa、T=3 800 K,峰值壓力為P=3.31 MPa,文獻[14]中結果為D=1 630 m/s、ρCJ=2.48 kg/m3、uCJ=681 m/s、PCJ=1.91 MPa、T=3 800 K,與A.J.Tulis等[15]由實驗中得到的鋁粉塵爆速1 650 m/s符合較好。

3 變密度下雙粉塵在空氣中的爆轟模擬

由于炸藥顆粒與鋁顆粒混合爆轟問題的復雜性,我們還研究了顆粒定直徑下的爆轟波波速及峰值壓力隨密度的變化關系。炸藥密度565 g/m3、半徑為10 μm,鋁粉塵半徑為3.5 μm,起爆條件為φ1=1、ρ1=2.2 kg/m3、u1=2 000 m/s、T1=3 200 K。粉塵從左端起爆,邊界條件為左端封閉,右端開口。如圖2～3所示,通過擬合關系可以看出,在不改變炸藥顆粒密度的情況下，爆轟波波速和峰值壓力基本隨密度呈線性關系。

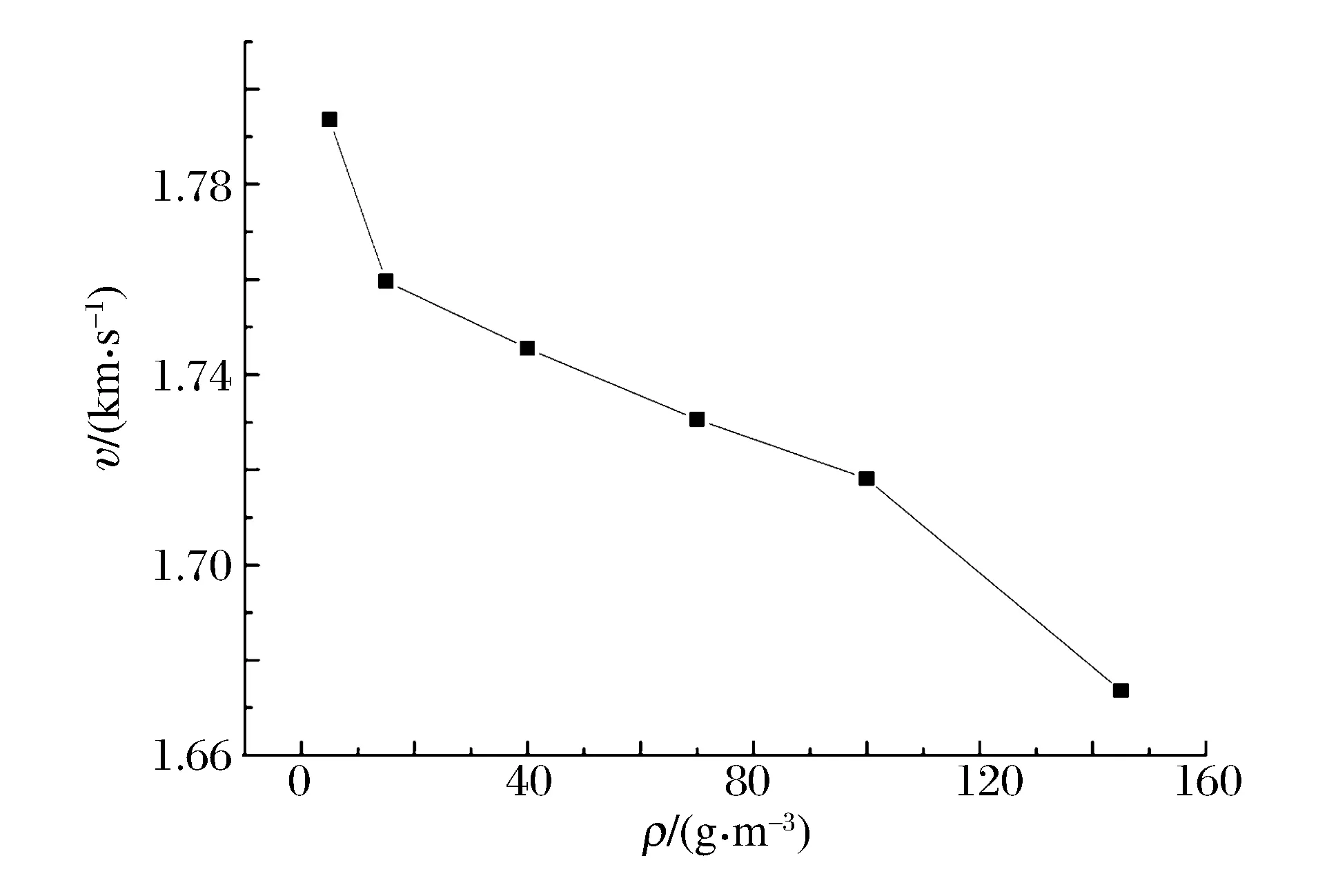
圖2 爆轟波速度隨雙粉塵中鋁粉塵密度的變化Fig.2 Wave speed varying with dust density

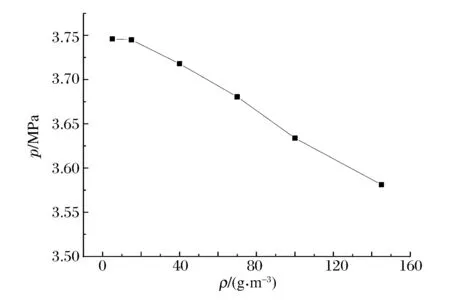
圖3 爆轟波壓力隨雙粉塵中鋁粉塵密度的變化Fig.3 Detonation pressure varying with dust density

4 復雜通道中的爆轟模型

模擬了在復雜通道中兩種粉塵的起爆及爆轟波傳播模型,模型如圖4所示,通道長3.2 m、寬1.5 m、障礙物長0.4 m、寬0.4 m,分別位于0.5、1.4和2.3 m處,網格數為600×240。炸藥顆粒密度為450 g/m3、半徑為20 μm,鋁顆粒密度為140 g/m3、半徑為2 μm。從左端起爆,起爆條件為φ1=1、ρ1=10 kg/m3、u1=1 000 m/s、T1=3 000 K,邊界條件為左端封閉、右端為開口,其余為固壁。選取坐標分別為A(0.25,0.75)、B(1.15,0.75)、C(1.15,0.25)、D(2.05,0.75)、E(2.05,0.25)、F(3.0,0.75)、G(3.0,0.25)的7個點進行研究。

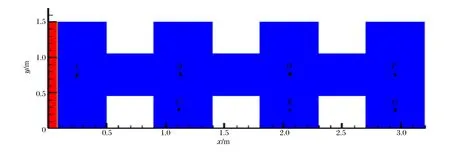
圖4 模擬區域幾何模型Fig.4 Geometrical model of simulated area

圖5為爆轟波在復雜通道中傳播的壓力圖,p1代表氣體流場壓力。在0.318 ms時,爆轟波到達0.7 m處,與0.5 m處障礙物發生反射,形成反射沖擊波,在第1個障礙物左固壁處形成高壓區域,局部壓力達到7 MPa；0.568 ms時,爆轟波到達1.15 m處,爆轟波從狹窄通道進入寬闊區域發生繞射,在拐角區域形成低壓區域,在通道左端可見兩道明顯的左行反射波,反射波經過0.5 m處拐點形成向右繞射波,并與爆轟波形成疊加,在爆轟波最右端可見明顯高壓區域；0.871 ms時爆轟波進入第2段狹窄通道,與第2障礙物左固壁形成的反射波與初始沖擊波疊加形成4個高壓奇點,并在通道左端可見反射形成第2道右傳沖擊波；1.178 ms時,爆轟波最右端形成高壓區域,由于爆轟波繞射拐角處出現低壓區域,而第2段寬闊通道內由于各種反射波的相互作用,流場變得復雜,形成了2個高壓區域；1.648 ms時在第3段寬闊通道內形成了類似0.871 ms時第2段寬闊通道內的高壓區域,而此時第2段寬闊通道內的2個高壓區向上運動疊加形成了蘑菇狀的高壓區域。

圖6中從左至右依次為點A(0.25,0.75)、B(1.15,0.75)、D(2.05,0.75)、F(3.0,0.75)處的壓力值隨時間變化曲線。在爆轟波向右傳播過程中逐漸趨于穩定,可以看出當爆轟波到達D點時,已經變成穩定爆轟,此時爆轟波壓力3.44 MPa,爆轟波傳播速度為1 656.78 m/s。從C、D2點的壓力值曲線圖中可以見到明顯的2個峰值,第1個峰值為初始爆轟波形成,第2個峰值為爆轟波在與壁面作用形成的反射波。

圖7中曲線從左到右依次為A(0.25,0.75)、B(1.15,0.75)、D(2.05,0.75)、F(3.0,0.75)點處的溫度隨時間變化曲線。從B、D、F這3點的溫度曲線可以看出,當爆轟波到達時,溫度迅速提升到3 400 K左右,而后溫度經過緩慢下降,在反射波到達后溫度會再次小幅度升高,流場溫度始終保持在3 000 K以上。

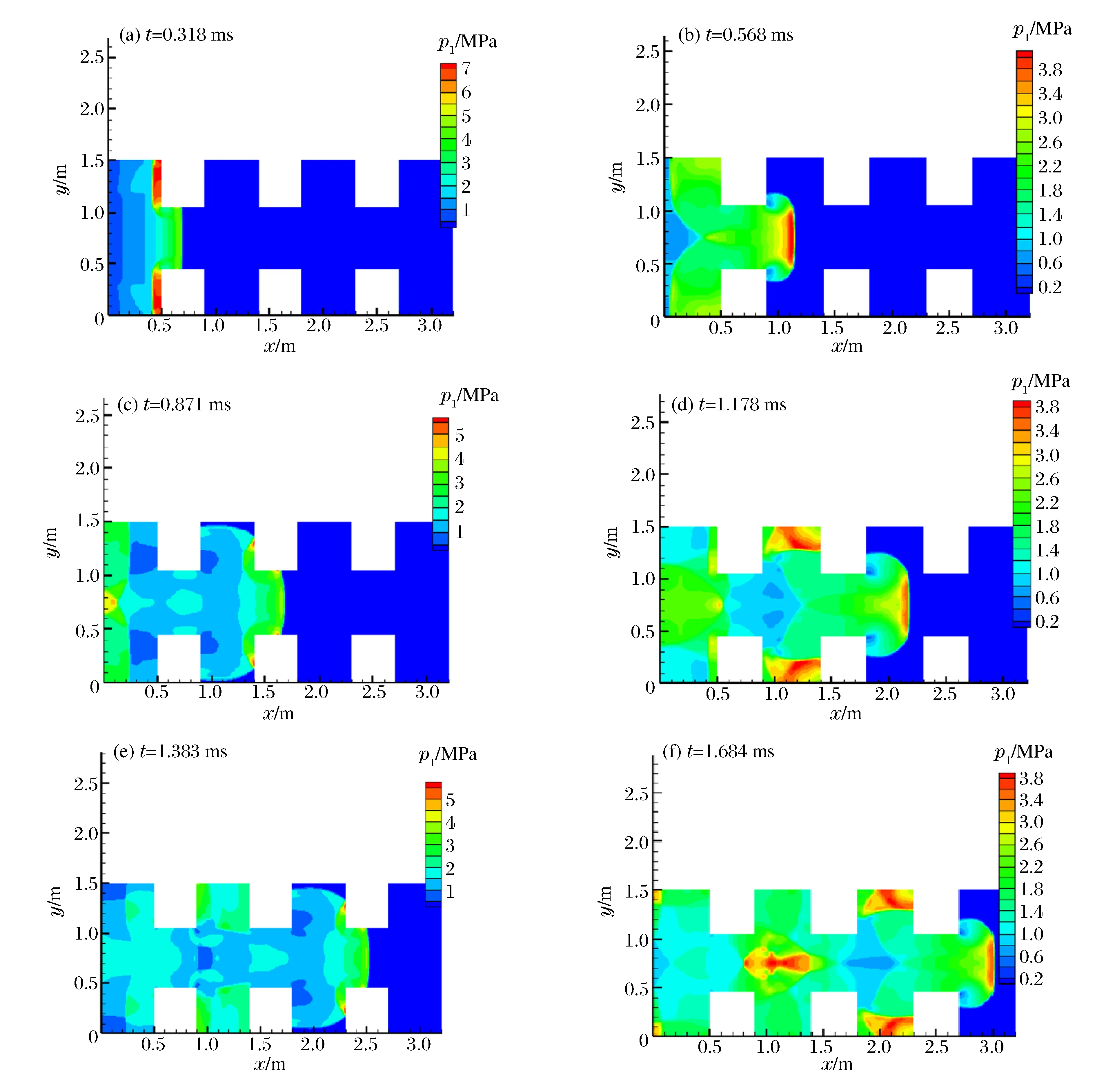
圖5 不同時刻流場壓力演化圖Fig.5 Detonation pressure varying with time

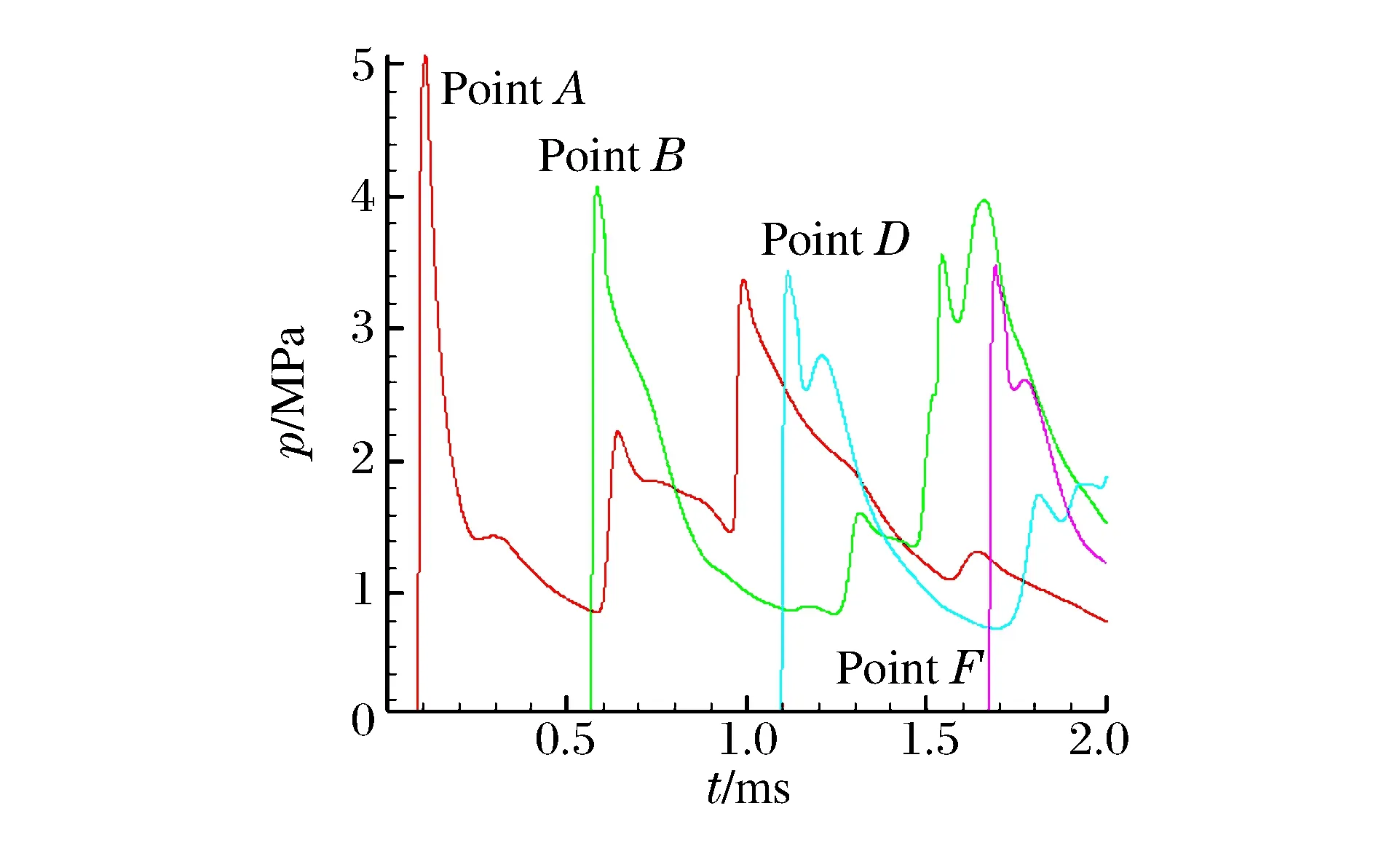
圖6 不同點的壓力隨時間變化曲線Fig.6 Pressure varying with time at different points

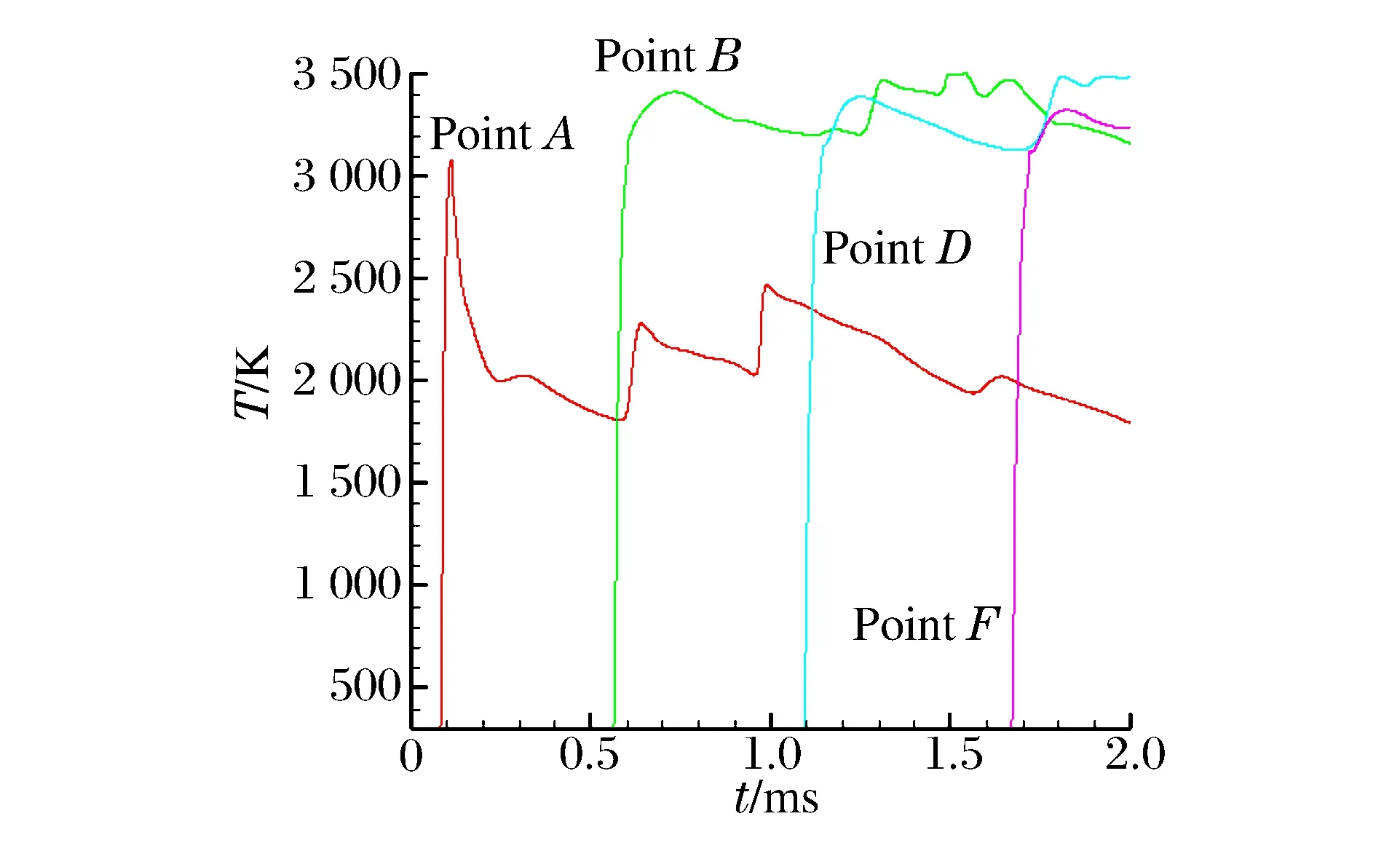
圖7 不同點的溫度隨時間變化曲線Fig.7 Temperature varying with time at different point

對比模擬了鋁顆粒單顆粒懸浮粉塵在同種情況下的爆轟過程,圖8中曲線從左到右依次為A(0.25,0.75)、B(1.15,0.75)、D(2.05,0.75)、F(3.0,0.75)點處的壓力隨時間變化曲線。對比圖6可以看出,到達穩定爆轟的距離也變長,流場壓力峰值比雙顆粒情況低約1 MPa,模擬得到的爆轟波傳播速度約為1 468.25 m/s,遠小于雙顆粒情況。對比圖6與圖8,在F點處都為穩定爆轟狀態,而雙粉塵爆轟時爆轟波經過F點處,壓力下降非常明顯,說明此時爆轟波寬度較窄,而單顆粒情況下壓力下降比雙粉塵時明顯變緩,說明此時爆轟波的反應區明顯加大。圖9中曲線從左到右依次為A(0.25,0.75)、B(1.15,0.75)、D(2.05,0.75)、F(3.0,0.75)點處的溫度隨時間變化曲線。流場溫度變化規律與雙顆粒情況基本相同,但是流場溫度明顯低于雙顆粒情況,并且流場溫度變化范圍高于雙顆粒情況。

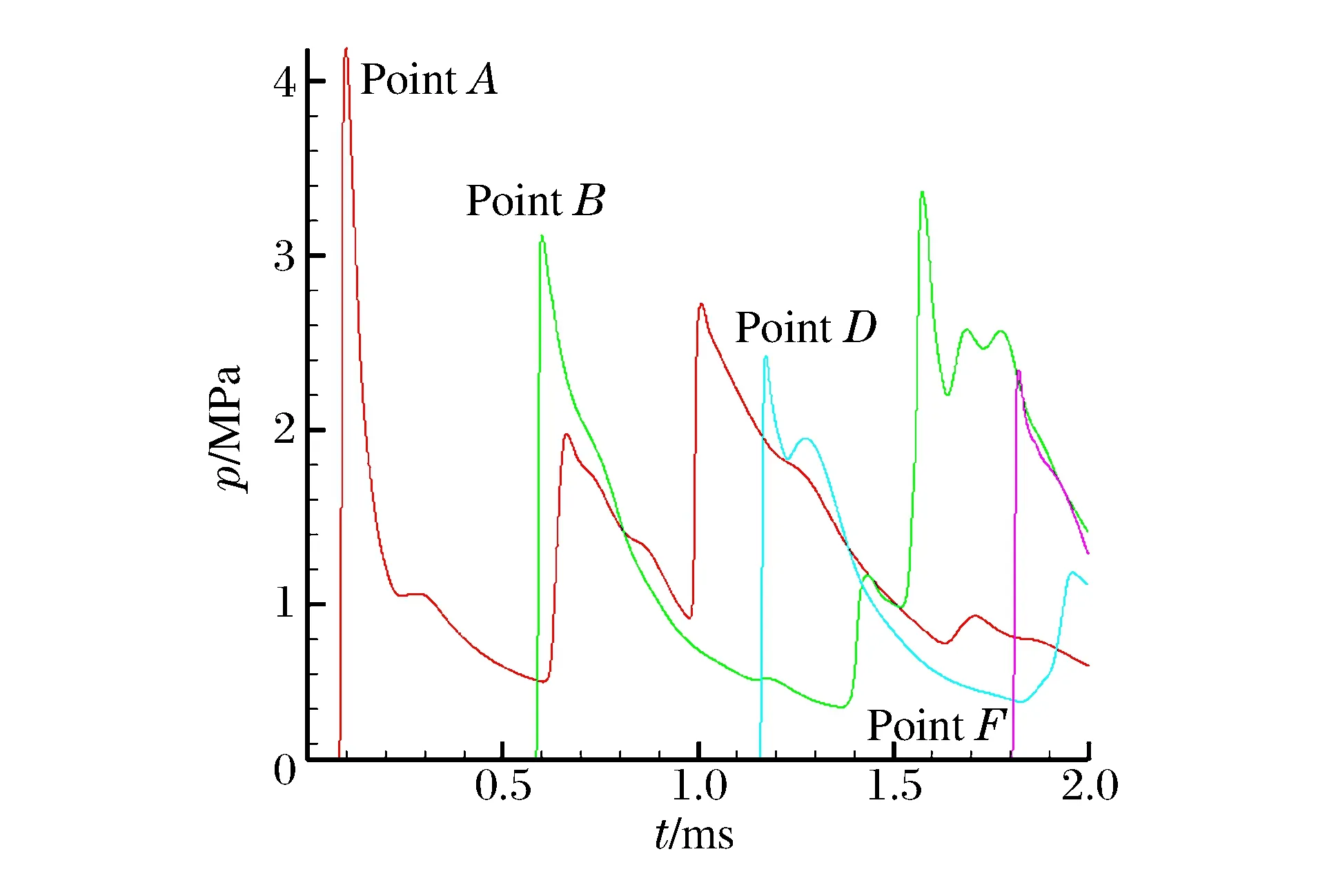
圖8 鋁單顆粒時不同點的壓力隨時間變化曲線Fig.8 Pressure varying with time at different points of Al

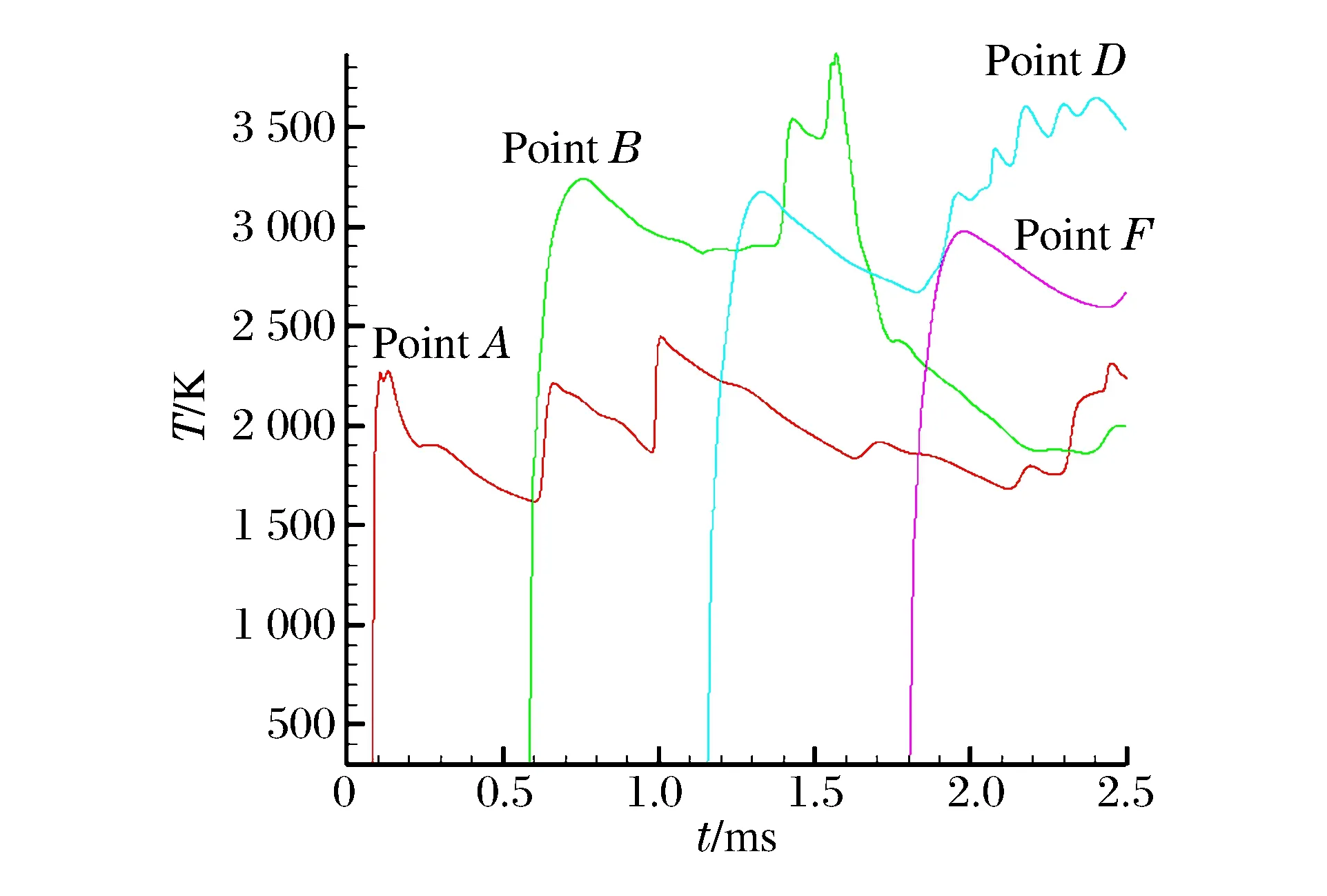
圖9 鋁單顆粒時不同點的溫度隨時間變化曲線Fig.9 Temperature varying with time at different points of Al

5 結 論

用CE/SE方法模擬了空氣中懸浮炸藥-鋁粉塵的二維爆轟模型,通過對比文獻驗證了模型程序的正確性。研究了雙粉塵爆轟過程中顆粒密度對爆轟波速度、爆轟波壓力的影響,得到了關于顆粒密度與波速壓力的線性關系。模擬了炸藥顆粒密度為450 g/m3、半徑為20 μm,鋁顆粒密度為140 g/m3、半徑為2 μm的懸浮粉塵在復雜通道中的傳播過程及流場演化過程,對比單種鋁顆粒在同種情況下的爆轟波過程發現,雙顆粒爆轟明顯提高了流場的峰值壓力、溫度及爆轟波傳播速度,并且爆轟波后的流場溫度要比單顆粒的更穩定。

很好地模擬了雙粉塵的兩相爆轟過程,為以后研究多粉塵復雜情況下的爆轟奠定了基礎。本次模擬研究了微米尺度下顆粒的爆轟過程,在納米尺度下粉塵放能加快,爆轟過程更復雜,在以后的模擬中還要對納米尺度下多種粉塵的爆轟過程進行細致的研究。

[1] 惠君明,劉榮海,葛桂蘭.提高FAE威力的研究(Ⅰ)----高能量燃料的選擇[J].南京理工大學學報,1995,19(5):472-476. Hui Junming, Liu Yonghai, Ge Guilan. Study on increasing the power of FAE(Ⅰ)-selection of high energy fuels[J]. Journal of Nanjing University of Science and Technology, 1995,19(5):472-476.

[2] 陳朗,張壽齊,趙玉華.不同鋁粉尺寸含鋁炸藥加速金屬能力的研究[J].爆炸與沖擊,1999,19(3):l-7. Chen Lang, Zhang Shouqi, Zhao Yuhua. Study of the metal acceleration capacities of aluminized explosives with spherical aluminum particles of different diameter[J]. Explosion and Shock Waves, 1999,19(3):l-7.

[3] 洪滔,秦承森,林文洲.懸浮RDX炸藥和鋁顆粒混合粉塵爆轟的數值模擬[J].爆炸與沖擊,2009,29(5):468-473. Hong Tao, Qin Chengsen, Lin Wenzhou. Numerical simulation of detonation in suspended mixed RDX and aluminum dust[J]. Explosion and Shock Waves, 2009,29(5):468-473.

[4] Chang S C. The method of space-time conservation element and solution element-A new approach for solving the Navier-Stokes and Euler equations[J]. Journal of Computational Physics, 1995,119(2):295-324.

[5] Wu Y, Yang V, Chang S C. Space-time method for chemically reacting flows with detailed kinetics[M]. Heidelberg: Springer Berlin Heidelberg, 2001:207-212.

[6] Dong Hefei, Hong Tao, Zhang Deliang. Application of the CE/SE method to a two-phase detonation model in porousmedia[J]. Chinese Physics Letters, 2011,28(3)：30203-30206.

[7] Zhang D L, Wang J T, Wang G. High-order CE/SE method and applications[J]. Chinese Journal of Computational Physics, 2009,26(2):211-220.

[8] Wang J T, Zhang D L, Liu K X. A Eulerian approach based on CE/SE method for 2D multimaterial elastic-plastic flows[J]. Chinese Journal of Computational Physics, 2007,24(4):395-401.

[9] 洪滔,林文洲.激波管中懸浮炸藥粉塵爆轟的數值模擬[J].高壓物理學報,2010,24(1):15-20. Hong Tao, Lin Wenzhou, Qin Chengsen. Numerical simulation of suspended RDX dust detonation in a shock tube[J]. Chinese Journal of High Pressure Physics, 2010,24(1):15-20.

[10] Price E W. Combustion of metalized propellants[C]∥Progress in Astronautics and Aeronautics: Fundamenals of Solid-Propellant Combustion,AIAA. New York, 1984,90:479-513.

[11] Steinberg T A, Wilson D B, Benz F. The combustion phase of burning particle[J]. Combustion and Flame, 1992,91(2):200-208.

[12] Eidelman S, Yang X L. Detonation wave propagation in combustible particle/air mixture with variable particle density distributions[J]. Combustion Science and Technology, 1993,89:201-218.

[13] 董賀飛,洪滔,張曉立.CE/SE方法數值模擬炸藥粉塵爆轟[J].中國計算物理通訊,2012,29(4):495-502. Dong Hefei, Hong Tao, Zhang Xiaoli. Numerical simulation of explosive dust detonation with CE/SE method[J]. Chinese Journal of Computational Physics, 2012,29(4):495-502.

[14] 洪滔,秦承森.懸浮鋁粉塵爆轟波參數[J].含能材料,2004,12(3):129-133. Hong Tao, Qin Chengsen. Parameters of detonation in suspended aluminum dust[J]. Energetic Materials, 2004,12(3):129-133.

[15] Tulis A J, Selman J R. Detonation tube studies of aluminum particles dispersed in air[J]. Symposium on Combustion, 1982,19(1):655-663.

(責任編輯 曾月蓉)

Numerical simulation of two-phase detonation of suspending RDX-Al dust in air with CE/SE

Zan Wentao1,2, Hong Tao2, Dong Hefei2

(1.BeiJingInstituteofTechnology,Beijing100088,China;2.InstituteofAppliedPhysicsandComputationalMathematics,Beijing100088,China)

In the present work we studied the detonation of Al-RDX suspended in air using CE/SE. The two-phase detonation process of two dusts with different density were simulated and the effects of different particle density on the detonation wave speed and pressure were investigated. It was found that there is a linear relationship between the density ratio and the wave speed and pressure. The flow field evolution of the two dusts detonation in a complex channel was discussed. Compared with the single dust detonation, the detonation wave speed, pressure, and temperature of the two dusts detonation were obviously higher. It is shown that CE/SE is an ideal method at present to simulate the two dusts detonation and can provide useful reference for multi-dust detonation study.

mechanics of explosion; dust detonation; CE/SE; RDX-Al dust

10.11883/1001-1455(2016)05-0603-08

2015-02-10； < class="emphasis_bold">修回日期：2016-01-20

2016-01-20

昝文濤(1988— ),男,博士研究生;

洪 滔,hongtao@iapcm.cn。

O381 <國標學科代碼：13035 class="emphasis_bold"> 國標學科代碼：13035 文獻標志碼：A國標學科代碼：13035

A