基于FLUENT-EDEM耦合的爆炸拋擲特性研究*

顧 強,張世豪,安曉紅,張 亞

(中北大學機電工程學院，山西 太原 030051)

基于FLUENT-EDEM耦合的爆炸拋擲特性研究*

顧 強,張世豪,安曉紅,張 亞

(中北大學機電工程學院，山西 太原 030051)

為了研究彈丸起爆后巖土碎屑的拋擲特性,針對爆炸后侵徹通道內(nèi)復(fù)雜的氣固兩相流動問題，提出了一種FLUENT軟件與EDEM軟件聯(lián)合的數(shù)值模擬方案，分析了不同深徑比條件下鉆地通道內(nèi)介質(zhì)碎屑的拋擲過程。進一步研究了介質(zhì)碎屑運移特性的影響因素。結(jié)果表明：介質(zhì)碎屑的運移能力與爆炸荷載峰值成正比，與鉆地通道深徑比及碎屑粒徑成反比。

爆炸力學；拋擲特性;FLUENT-EDEM;碎屑粒徑;爆炸荷載;深徑比

隨著軍事科技的發(fā)展，現(xiàn)代戰(zhàn)爭已從地面、海上和空中的較量向太空、地下和深海方向發(fā)展。為了防御大規(guī)模殺傷性武器的襲擊，針對高價值重要軍事目標,世界各國的地下掩體日益堅固化[1-2]。鉆地彈侵徹目標介質(zhì)時，隨著深度的不斷增加，堆積在鉆地通道底部的破碎介質(zhì)勢必會阻礙鉆地類武器的繼續(xù)侵徹。基于此，研究侵徹彈丸起爆碎屑的拋擲特性，對于研發(fā)新型鉆地武器，提高鉆地彈毀傷目標的能力，具有重要的意義。

由分析可知，該物理模型的本質(zhì)為爆炸荷載作用下侵徹通道內(nèi)的氣固兩相流動問題。因此，本文中首先運用氣固兩相流理論[3]，提出流體動力學軟件FLUENT與離散元軟件EDEM聯(lián)合的數(shù)值模擬方案，對深徑比分別為2/3、8/3的侵徹通道內(nèi)介質(zhì)碎屑受爆炸荷載作用下的流動運移特性進行分析，并進一步討論碎屑運移特性的影響因素。文中涉及的模擬數(shù)據(jù)結(jié)果均由FLUENT軟件及EDEM軟件聯(lián)合計算所得，兩者缺一不可。在分析碎屑顆粒體積分數(shù)時運用了FLUENT軟件中的顆粒體積分數(shù)云圖，其余的數(shù)據(jù)均是在EDEM軟件中提取。

1 EDEM軟件與FLUENT軟件耦合

當前針對侵徹通道內(nèi)氣體流動的CFD模擬，雖然得到了模擬區(qū)域內(nèi)的體積分數(shù)的分布，但對于處于離散狀態(tài)的固體顆粒與顆粒(物料)間，以及顆粒與通道壁間力的作用無法精確計算，從而大大降低對碎屑的運動精度[4]。所以，經(jīng)過深入研究，聯(lián)合FLUENT軟件與EDEM軟件耦合模擬。

1.1 氣固耦合控制方程

顆粒相與氣體相的耦合模型中主要包括Eulerian-Lagrangian法和Eulerian-Eulerian法[5-6]。由于Eulerian-Eulerian法是基于多相流框架的耦合方法，更加適用于密相兩相流問題，因為它可以加入顆粒相對氣體相的作用力，可包含質(zhì)量、動量和能量的交換。因此本文中選用Eulerian-Eulerian法對侵徹通道內(nèi)爆炸荷載作用下的碎屑運移進行模擬。Eulerian-Eulerian法耦合控制連續(xù)性方程和N-S方程為：

(1)

式中:ρg為氣體密度，t為時間，ug為氣體速度，εg為氣體空隙率，p為氣體壓力，μg為氣體動力黏度，g為重力，S為動量交換源相。

在氣固兩相流中，顆粒i的運動規(guī)律遵循牛頓第二定律：

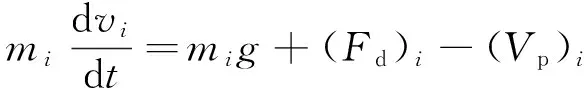
(2)

式中:mi、vi、(Vp)i分別表示顆粒i的質(zhì)量、速度和體積；(Fd)i、pi表示顆粒i的曳力和壓力梯度。

將巖土碎屑和侵徹通道材料定義為巖土，彈體材料定義為鋼，其中，碎屑-碎屑，碎屑-彈體，碎屑-壁面受力計算采用Hertz模型，具體參數(shù)如表1所示。其中巖土與鋼的密度取實驗測量的平均值，泊松比通過查閱文獻[7]得到，剪切模量通過相關(guān)計算公式得到。

表1 材料參數(shù)Table 1 Material parameters

1.2 計算模型

為了更好地分析不同鉆地通道深度下的碎屑運移特性，取深徑比γ作為衡量侵徹通道深度的指標。當深徑比γ=2/3、8/3時，侵徹過程形成的通道近似可表示為圓柱直筒型通道，外界空氣近似看作圓筒型，并且兩圓筒相連。圖1為深徑比γ=8/3的侵徹通道的物理模型及幾何模型圖。其中，侵徹通道直徑為0.15 m，高度為0.4 m。外界空氣圓柱直徑為6 m，高度為2 m。將入口邊界定義為速度入口，將出口邊界條件定義為壓力出口，其出口氣體壓力為1個標準大氣壓(1.01×105Pa)，并均勻分布。另外，將侵徹通道壁面定義為無滑移的氣相速度邊界條件。

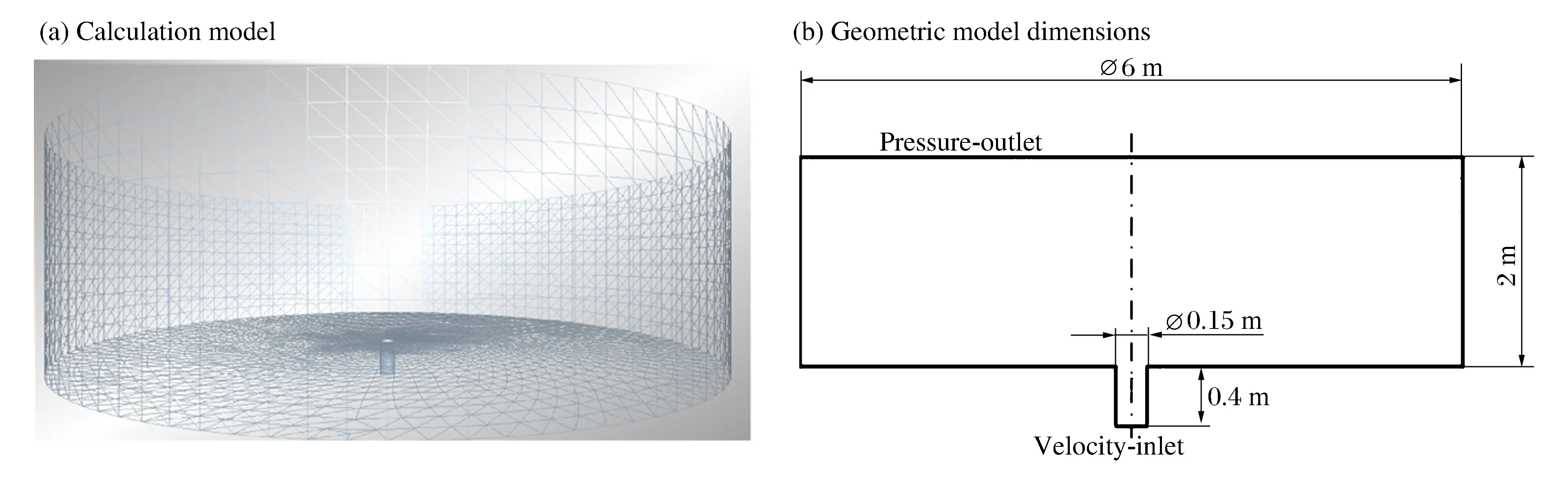
圖1 深徑比γ=8/3時計算模型Fig.1 Calculation model for a depth-diameter ratio γ as 8/3

1.3 模型驗證

為驗證耦合模擬模型及材料參數(shù)的合理性，將數(shù)值模擬結(jié)果與理論計算結(jié)果進行比較。文獻[8]認為碎屑最大拋距為:

Lmax=v2/g

(3)

式中:Lmax為碎屑顆粒最大拋擲距離，v為碎屑初速度，g=9.81 m/s2。

將上式進行量綱一分析，則式(3)可變?yōu)?/p>

n=tanα=v2/(gH)

(4)

式中:n為拋擲指數(shù)，H為爆坑深度，如圖2所示。

圖3為侵徹通道深度H與拋擲指數(shù)n的關(guān)系曲線圖。由圖3可知，理論結(jié)果擬合曲線與數(shù)值模擬結(jié)果擬合曲線走勢大致相同。當通道深度低于0.4 m時，曲線斜率較大；當坑深大于0.4 m時，兩者曲線平緩，斜率變小。由巖土中爆炸相似定律可知，本文中所建物理模型和各參數(shù)設(shè)置較為合理。

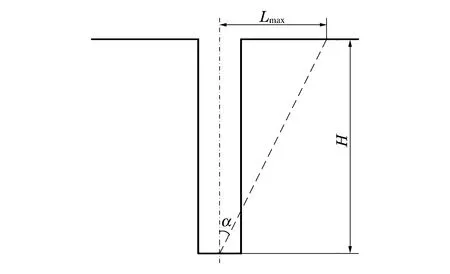
圖2 拋擲爆炸示意圖Fig.2 Schematic of throw explosion

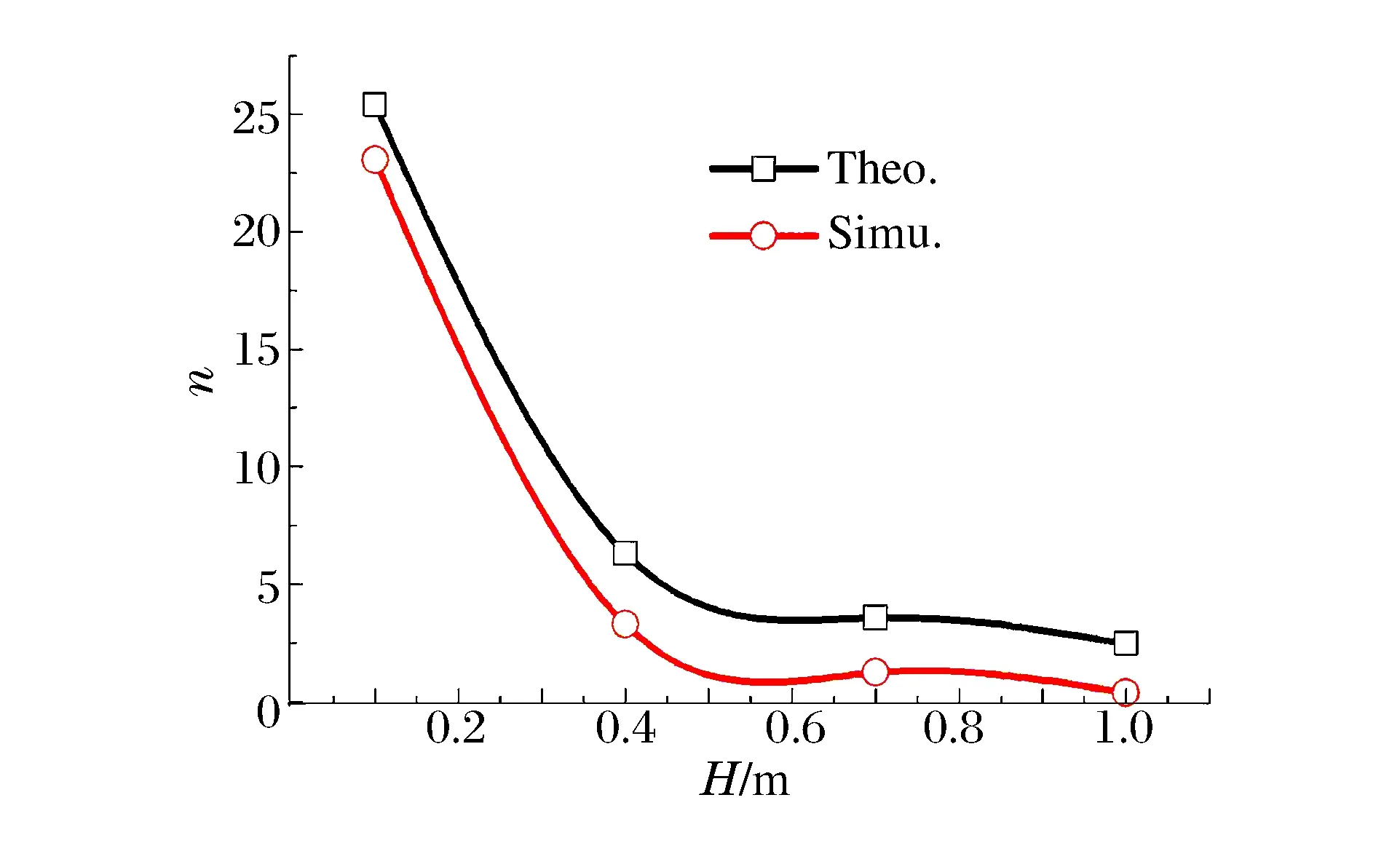
圖3 侵徹通道深度與拋擲指數(shù)關(guān)系曲線Fig.3 Curves of channel depth vs. throw exponential

2 模擬結(jié)果分析

2.1 拋擲特性分析

圖4給出了侵徹通道深徑比γ=2/3(即通道尺寸為?0.15 m×0.1 m)、γ=8/3(即通道尺寸為?0.15 m×0.4 m)時對稱軸上碎屑體積的分布曲線。從圖4(a)可以看出，當深徑比γ=2/3時，0.1 s時刻碎屑受爆炸荷載的驅(qū)動被拋出通道，在軸向0.5 m處碎屑體積分數(shù)達到峰值，約為0.006。約在0.4 s時達到最高點，體積分數(shù)在1.0 m時達到峰值0.001 5。此后開始下落，1.0 s時少數(shù)巖土碎屑落回至通道底部，大部分碎屑散落在水平面，碎屑整體開始向徑向擴散，體積分數(shù)逐漸下降，在0.4 s時刻后，巖土碎屑整體下降，最后在1.0 s時刻體積分數(shù)變?yōu)?。當深徑比γ=8/3時，結(jié)合圖4(b)可知，0.1 s時刻碎屑運移至爆坑上端口，但受到侵徹通道壁面的約束，體積分數(shù)較高，約為0.075。隨著時間的推移，碎屑整體持續(xù)向上運動，并且開始徑向擴散，在0.4 s時刻運移至最高處1 m左右，但碎屑體積分數(shù)峰值降低為0.01。此后，碎屑開始下降，最后降落至水平面，其相應(yīng)的體積分數(shù)也變?yōu)?。

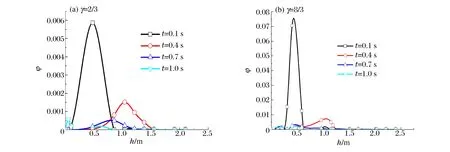
圖4 不同深徑比下對稱軸上碎屑體積分布Fig.4 Debris volume distribution on symmetrical axis with different γ

2.2 影響因素分析

2.2.1 爆坑深度

圖5為侵徹通道深徑比與拋擲距離x的關(guān)系。由圖5可知，隨著通道深徑比的增加，拋擲距離逐漸減小，在γ=2/3時拋擲距離最大，約為2.5 m；而在γ=20/3時拋擲距離最小，約為0.4 m。究其原因，當侵徹通道變深，碎屑與壁面發(fā)生碰撞次數(shù)變多，消耗能量較大，故作用在拋擲方面的能量相應(yīng)減小，相應(yīng)的拋擲距離也變小。

綜上所述，拋擲距離與侵徹通道深徑比成反比關(guān)系，即鉆地通道越淺，其碎屑拋擲距離越大，運移能力越強。

2.2.2 爆炸荷載峰值

針對爆炸載荷特征參數(shù)，本文中重點討論荷載峰值對碎屑運移特性的影響規(guī)律。取鉆地通道深徑比γ=2/3進行研究，其中氣流速度荷載峰值分別取為30、50、70 m/s。

圖6～7分別給出了不同荷載峰值條件下，0.4 s時刻深徑比γ=2/3的通道內(nèi)爆炸碎屑體積分數(shù)云圖及對稱軸上碎屑體積分布。結(jié)合圖6～7可以看出，隨著載荷峰值的逐漸增加，對稱軸上碎屑體積分數(shù)峰值由0.001 8降低為0.001 3。由此可知，載荷峰值對碎屑運移影響較大，即隨著載荷峰值的增加，同一高度下碎屑顆粒數(shù)目減小，相應(yīng)的體積分數(shù)較低。

圖8給出了不同荷載峰值條件下碎屑拋擲高度與拋擲距離。從圖8可知，隨著荷載峰值的增加，相應(yīng)的拋擲高度y與拋擲距離x均逐漸變大，但是拋擲距離的斜率明顯大于拋擲高度的斜率。由于氣流的荷載峰值增大，其攜帶的碎屑初速度變大，故拋擲高度逐漸變大。綜上可知，不同荷載峰值對深徑比γ=2/3時碎屑運移特性影響較大，隨著荷載峰值的增大，碎屑拋擲距離與拋擲高度變大，但是對拋擲距離的影響更大。所以，荷載峰值與運移特性成正比，即荷載峰值越大運移能力越好。

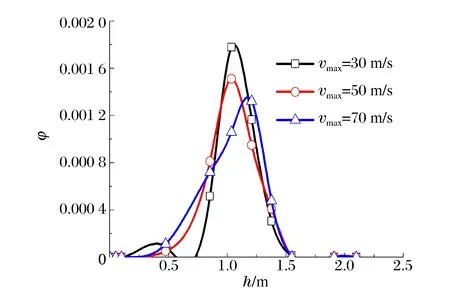
圖7 不同荷載峰值條件下碎屑體積分數(shù)分布曲線Fig.7 Curves of volume fractionunder different loading

圖8 拋距x、拋高y隨著荷載的變化Fig.8 Variation of throw distance x andthrow height y with loading

2.2.3 碎屑粒徑

在軟件模擬計算過程中，碎屑顆粒半徑遵循正態(tài)分布，平均半徑為1 mm，標準差為0.1 mm。故針對碎屑的特征參數(shù)，本文中重點討論碎屑顆粒平均直徑對其運移特性的影響規(guī)律。取鉆地通道深徑比γ=2/3進行研究，其中碎屑平均直徑分別取為1、2、3 mm。

圖9～10分別給出了不同碎屑直徑條件下，鉆地通道深徑比γ=2/3在0.4 s時刻碎屑體積分數(shù)云圖及對稱軸上碎屑體積分布。結(jié)合圖9～10可以看出，隨著碎屑直徑的增加，3種工況下碎屑體積分數(shù)云圖范圍逐漸減小，其中，碎屑直徑為3 mm時云圖范圍最小，但其碎屑體積分數(shù)峰值最大，約為0.001 3。由此可知，碎屑直徑對碎屑運移影響較大，即隨著直徑的增加，同一高度下碎屑顆粒數(shù)增多，碎屑運移能力越差。

圖11給出了不同碎屑直徑對碎屑拋擲高度與拋擲距離的影響。由圖可知，隨著碎屑直徑的增加，相應(yīng)的拋擲距離逐漸變小，拋擲高度先增大后減小。究其原因，由于碎屑直徑增大，相同空間內(nèi)的碎屑間隙必然變小，發(fā)生碰撞的幾率增多，能量損失較大；另一方面，碎屑的質(zhì)量與碎屑直徑成正比，即重力變大。綜上可知，不同碎屑直徑對近地表條件下碎屑運移特性影響較大，隨著平均直徑的增大，其運移能力逐漸變差。

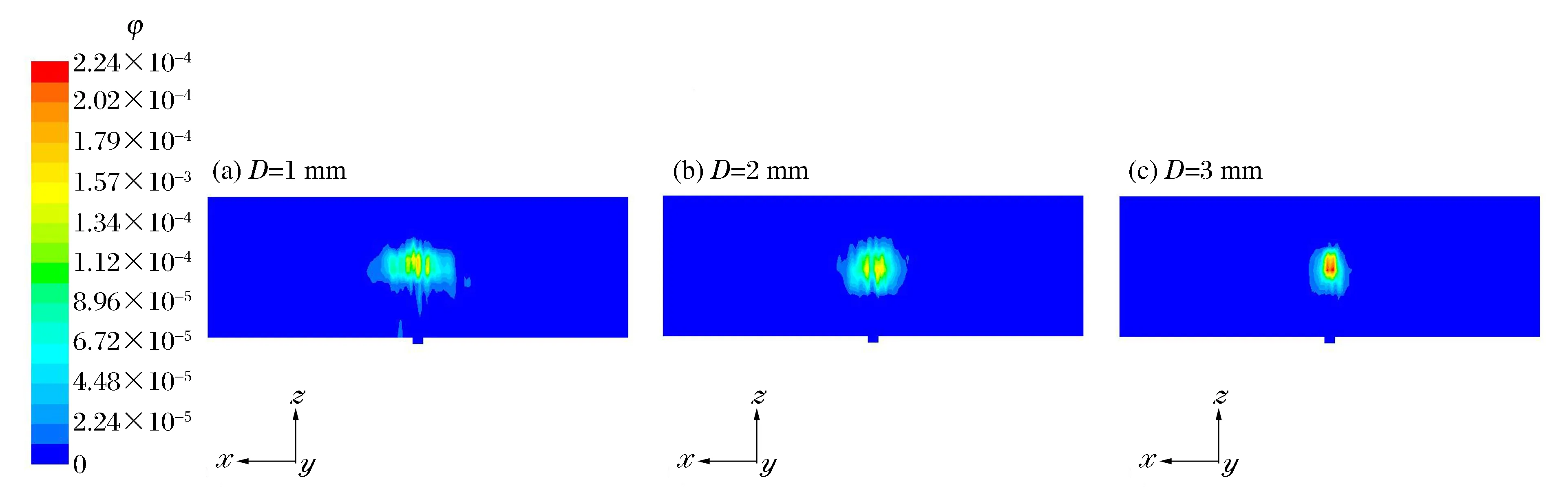
圖9 不同碎屑直徑下通道內(nèi)碎屑體積分數(shù)云圖Fig.9 Debris volume fraction contours for different debris particle sizes

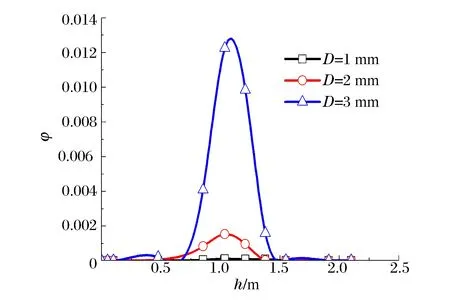
圖10 不同碎屑粒徑下碎屑體積分數(shù)分布曲線Fig.10 Curves of volume fraction underdifferent debris particle sizes

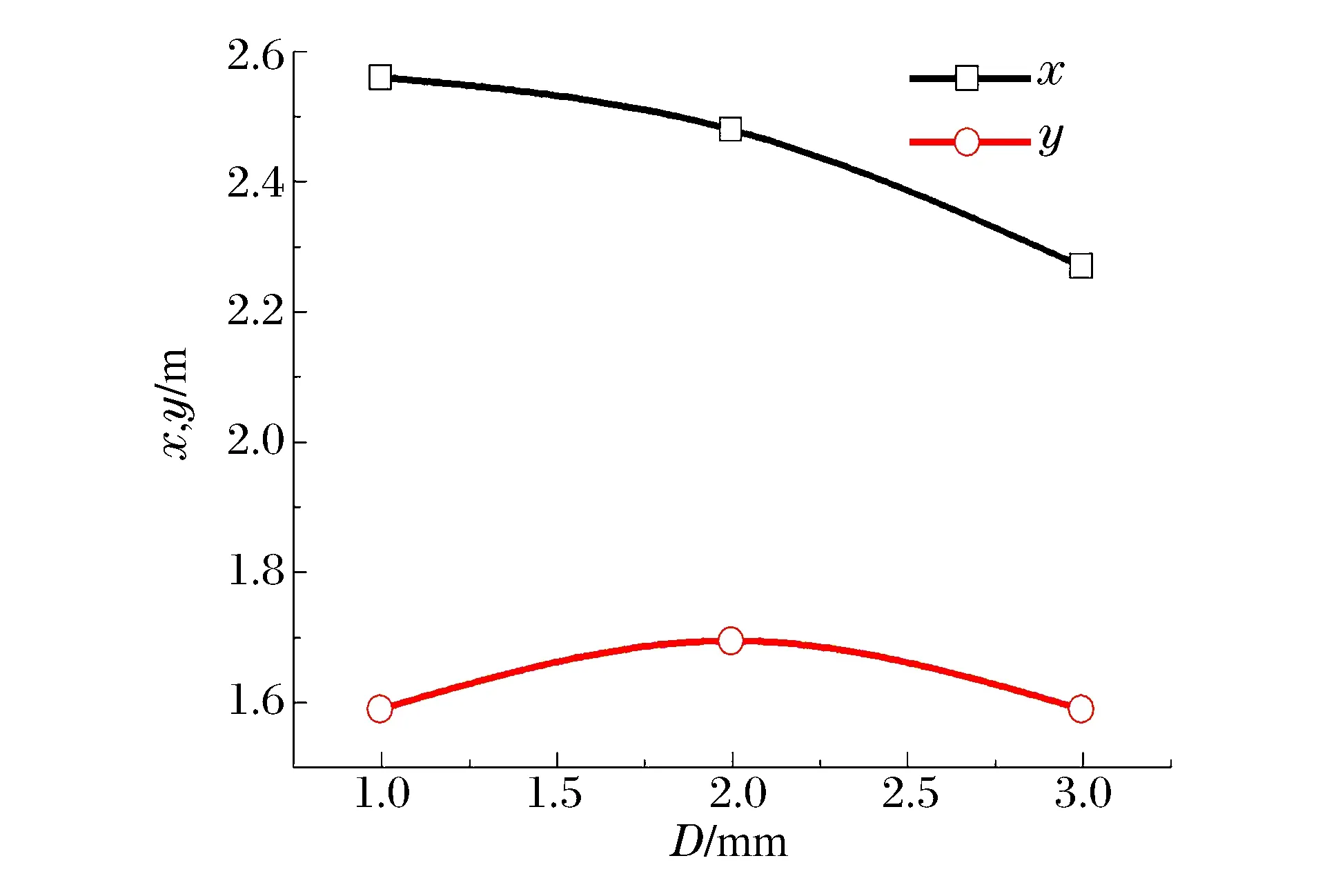
圖11 拋距x、拋高y隨著碎屑粒徑的變化Fig.11 Variation of throw distance x and throw height ywith debris particle size

3 結(jié) 論

(1)針對侵徹通道內(nèi)起爆后復(fù)雜的氣體流動問題，提出一種新型的CFD模擬方法，即聯(lián)合FLUENT軟件與EDEM軟件耦合模擬。通過采用Hertz-Mindlin無滑動接觸模型來模擬顆粒-顆粒和顆粒-邊界的接觸碰撞，以及采用具有相間耦合作用的Eulerian-Lagrangian 耦合算法，來近似模擬了鉆地通道內(nèi)起爆后介質(zhì)碎屑的運移特性。由模型的驗證可知，本文中所運用的模擬方法、物理模型和各參數(shù)設(shè)置較為合理。(2)當鉆地通道深徑比γ=2/3、8/3時，介質(zhì)碎屑開始時刻由于受到爆炸荷載作用整體向上運動，某時刻碎屑整體開始向徑向擴散，最后降落到水平面。另外，碎屑數(shù)量隨著與鉆地通道軸線距離的增大而逐漸變少。(3)研究了鉆地通道深徑比、爆炸荷載峰值、碎屑平均粒徑3個因素對介質(zhì)碎屑拋擲特性的影響。結(jié)合模擬結(jié)果可知，荷載峰值與碎屑拋擲特性成正比，荷載峰值越大，碎屑運移能力越好；而鉆地通道深徑比、碎屑平均粒徑與碎屑拋擲特性成反比，隨著數(shù)值變大，運移能力逐漸變差。

[1] 王濤,余文力,王少龍，等.國外鉆地武器的現(xiàn)狀與發(fā)展趨勢[J].導(dǎo)彈與航天運載技術(shù),2005(5):51-56. Wang Tao, Yu Wenli, Wang Shaolong, et al. Present status and tendency of foreign earth-penetrting weapons[J]. Missiles and Space Vehicles, 2005(5):51-56.

[2] 汪斌,曹仁義,譚多望.大質(zhì)量高速動能彈侵徹鋼筋混凝土的實驗研究[J].爆炸與沖擊,2013,33(1):98-102. Wang Bin, Cao renyi, Tan Duowang. Experimental study on penetration of reinforced concrete by a high-speed penetrator with large mass[J]. Explosion and Shock Waves, 2013,33(1):98-102.

[3] 袁竹林,朱立平,耿凡,等.氣固兩相流動與數(shù)值模擬[M].南京:東南大學出版社,2013.

[4] 潘振海,王昊,王習東,等.油砂干餾系統(tǒng)的DEM-CFD耦合模擬[J].天然氣工業(yè),2008,28(12):124-126. Pan Zhenhai, Wang Hao, Wang Xidong, et al. DEM-CFD coupled simulation of oil sands retorting in a rotary kiln[J]. Natural Gas Industry, 2008,28(12):124-126.

[5] 戚華彪,周光正,于福海.顆粒物質(zhì)混合行為的離散單元法研究[J].化學進展,2015,27(1):113-124. Qi Huabiao, Zhou Guangzheng, Yu Fuhai. Researches on mixing of granular materials with discrete element method[J]. Progress in Chemistry, 2015,27(1):113-124.

[6] 心男.基于EDEM-FLUENT耦合的氣吹式排種器工作過程仿真分析[D].長春:吉林大學,2013.

[7] 王國強,郝萬軍,王繼新.離散單元法及其在EDEM上的實踐[M].西安:西北工業(yè)大學出版社,2010.

[8] 張奇.球形裝藥巖石拋擲爆破初速度的數(shù)值模擬[J].煤炭學報,1993,18(5):27-32. Zhang Qi. Numerical modelling of initial speed of throw blasting using spherical charge[J]. Journal of China Coal Society, 1993,18(5):27-32.

(責任編輯 曾月蓉)

Research on throw characteristics of rock debris explosion based on coupled FLUENT-EDEM

Gu Qiang, Zhang Shihao, An Xiaohong, Zhang Ya

(CollegeofMechatronicEngineering,NorthUniversityofChina,Taiyuan030051,Shanxi,China)

In order to study the throw characteristics of rock debris after explosion, with a view of solving complicated problems involved in the two-phase gas-solid flow in a penetration channel, we propose a simulation scheme combining the use of FLUENT and EDEM softwares. Based on this scheme, we analyzed the medium debris’s blasting process for different depth-diameter ratios and studied the factors that bear on the debris’s transporting characteristics. The results show that debris transporting capability is directly proportional to the peak value of the explosion load, and is inversely proportional to the ratio of the channel depth to the channel diameter and the debris particle size.

mechanics of explosion; throw characteristics; FLUENT-EDEM; debris particle size; explosion load; depth to diameter ratio

10.11883/1001-1455(2016)05-0611-06

2015-03-20； < class="emphasis_bold">修回日期：2016-01-20

2016-01-20

顧 強(1961— )，男，碩士，教授，hg14gu@163.com。

O383 <國標學科代碼：13035 class="emphasis_bold"> 國標學科代碼：13035 文獻標志碼：A國標學科代碼：13035

A