膨脹柱殼恒定應變率的本構關系*
郭昭亮任國武張世文湯鐵鋼劉倉理
(1.中國工程物理研究院流體物理研究所,四川 綿陽 621999;2.中國工程物理研究院,四川 綿陽 621999)
膨脹柱殼恒定應變率的本構關系*
郭昭亮1,任國武1,張世文1,湯鐵鋼,劉倉理2
(1.中國工程物理研究院流體物理研究所,四川 綿陽 621999;2.中國工程物理研究院,四川 綿陽 621999)
考慮到金屬柱殼膨脹過程中隨機裂紋萌生對測試結果的可能干擾,設計了預置有中心穿透圓孔的柱殼樣品,采用多普勒光纖探針測量系統(tǒng)獲得了柱殼外壁更優(yōu)的徑向速度歷史。基于膨脹柱殼實驗中固有的非恒定應變率現(xiàn)象,研究了獲得恒定應變率下本構方程的方法,并采用改進后的本構方程確定方法,獲得了20鋼恒定應變率下的應力應變關系。
固體力學;本構方程;多普勒光纖探針;膨脹柱殼;恒定應變率
材料與結構在高應變率下的變形與破壞規(guī)律研究,對深入認識材料的動態(tài)響應機理以及工程防護有著重要的作用。爆炸膨脹環(huán)作為材料在高應變下動態(tài)力學性能的實驗手段,最早由P.C.Johnson 等[1]建立,后逐步發(fā)展為獲得高應變率拉伸加載下材料性能的重要工具。近年來,T. Hiroe等[2-3]采用線起爆技術研究了內部爆炸載荷作用下的材料動力學行為。在測試材料力學性能的實驗中,對試件的幾何設計有著嚴格的要求,以避免不合適的試件設計帶來的非材料因素的影響。湯鐵鋼等[4-7]討論了爆炸膨脹環(huán)一維應力假定,爆炸膨脹環(huán)實驗數(shù)據(jù)處理方法以及爆炸膨脹環(huán)界面尺寸效應等問題,并指出在爆炸膨脹環(huán)實驗研究中,適當增加膨脹環(huán)的寬度既可以提高加載應變率,又可以增加膨脹環(huán)運動的穩(wěn)定性。在此理念上,本文中發(fā)展了用于研究材料高應變率拉伸本構的膨脹柱殼樣品設計。R.H.Warnes等[8]曾指出,膨脹環(huán)實驗中應變率在實驗過程中減小,這并不是一個缺點,可以通過多次實驗畫出給定材料的應力-應變-應變率曲線。遺憾的是在其分析過程中依然采用了數(shù)據(jù)窗口中心的數(shù)據(jù)來計算應變率,這實際上依舊是采用平均應變率的概念,并未在應力應變關系中剝離應變率變化帶來的影響。尤其是對于應變率敏感材料,其動態(tài)力學性能將會隨應變率較小的變化而發(fā)生較大的改變,在材料的應力應變關系測試中需要將應變率的影響分離,進而獲得更清晰的認識。霍普金森壓桿(SHPB)實驗中,可以通過控制加載實現(xiàn)恒應變率條件下的測試[9],但膨脹環(huán)實驗中的非恒定應變率是由實驗的基本原理確定的,變化范圍太大,可能已經不能繼續(xù)選擇平均應變率這一概念。
為了獲得膨脹環(huán)、膨脹柱殼的恒定應變率本構關系,本文中首先分析爆炸柱殼實驗中非恒定應變率的由來;隨后針對金屬柱殼膨脹斷裂過程中隨機裂紋的萌生,設計預置中心圓孔的樣品,成功避免隨機裂紋萌生對測速的干擾;最后給出獲得金屬柱殼恒定應變率下本構關系的方法。
1 膨脹柱殼非恒定應變率起源
中心線起爆加載下的膨脹環(huán)、膨脹柱殼實驗中(實驗裝置示意圖見文獻[4]),一般采用試樣外壁的徑向速度歷史反演應力應變關系,膨脹柱殼的運動分析如圖1所示。

圖1 膨脹柱殼運動分析示意圖Fig.1 Schematic of dynamic analysis of expanding cylinder
在柱殼中心附近沿著z軸選取高度為dz的范圍,在自由飛行階段,金屬柱殼僅在環(huán)向應力σθ作用下做減速運動,假定材料不可壓,在靠近柱殼中心附近局域沿軸向的變形可以忽略不計。環(huán)向流動應力、應變、應變率分別為(理論分析類似于膨脹環(huán),見文獻[5]):
(1)
(2)
(3)
式中:ρ0為材料密度,r0為初始外半徑,r為隨時間變化的膨脹半徑,vr為瞬時速度。柱殼自由飛行階段,近似為平面應變狀態(tài)[10],σz=(σr+σθ)/2,σr=0,等效應力可寫為:
(4)
假定體積不可壓,應變之間的關系滿足:
εz=0
(5)
εr=-εθ
(6)
因此,等效塑性應變可寫為:
(7)
典型的膨脹柱殼外壁徑向速度曲線如圖2(a)所示,由公式(3)得到對應的應變率隨時間的變化,如圖2(b)所示。應變率在自由膨脹階段,從1.0×104s-1遞減至5.0s-1左右,在建模過程中,不能簡單采用應變率平均值描述材料的動態(tài)響應。
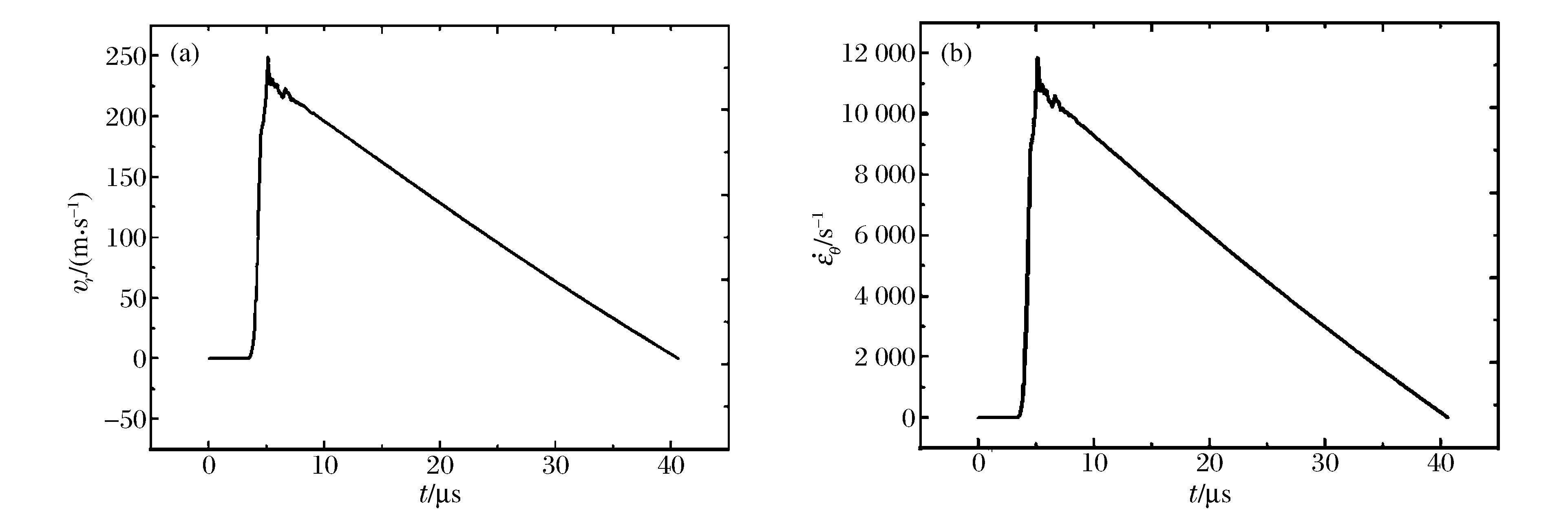
圖2 膨脹柱殼典型的速度、應變率隨時間的變化曲線Fig.2 Curves for typical velocity and strain rate of expanding cylinder
應變率隨著時間減小,是由膨脹環(huán)、柱殼實驗基本原理決定的,在實驗中無法避免。直接采用速度歷史獲得的應力應變關系本質上不同于應變率下的應力應變關系。一般地,我們希望獲得某一恒定應變率下的應力應變關系,以便建模;然而,由于爆炸膨脹環(huán)、柱殼特殊的幾何結構,造就了在整個膨脹變形過程中,應變率的非恒定性。為此,我們將通過一組20鋼爆炸膨脹柱殼實驗,建立獲得恒定應變下應力應變關系的方法。
2 實驗設計
膨脹柱殼實驗裝置示意圖如圖3(a)所示。諸實驗中驅動器為20鋼,幾何尺寸不變,炸藥采用泰安粉末均勻填裝于裝藥套筒,裝藥高度為56 mm,實驗參數(shù)如表1所示,表中r、R、h、D、m、ρ分別表示試樣內徑、試樣外徑、試樣高度、裝藥直徑、裝藥質量、裝藥密度。
實驗中除了裝藥量不同外,其他狀態(tài)完全一致,其中實驗2、3為重復性實驗。
實驗測試布局示意圖如圖3(b)所示,樣品為含有中心穿透圓孔(直徑為1 mm)的金屬柱殼,測速點位于圓孔正對的位置,以避免在測速點鄰近區(qū)域萌生裂紋,從而影響速度測量(不含預置缺陷的金屬柱殼在內部載荷作用下,裂紋將隨機萌生,測速點附近可能會受到局域卸載波的干擾,具體見實驗結果分析)。另一方面,我們采用高速攝影技術觀測預置缺陷局部的變形、裂紋萌生及裂紋擴展等現(xiàn)象,以此估計預置缺陷對測速點的干擾。
3 實驗結果與分析
采用激光干涉測速技術(DPS),獲得了20鋼柱殼實驗1~4的外壁徑向膨脹速度歷史,如圖4所示。20鋼柱殼自由膨脹階段持續(xù)約40~50 μs,由于裝藥量不同,20鋼柱殼的徑向速度響應不同,其中實驗2與實驗3為重復性實驗,在結構完全一致、裝藥量完全相同的情況下,由于裝藥密度微小的差異(0.6%),速度差異約為3.1%。從速度曲線可以得到,自由膨脹階段,20鋼實驗1~4的應變率變化范圍分別為6.14×103~0 s-1、8.62×103~8.1×102s-1、8.76×103~8.1×102s-1、1.01×104~2.6×103s-1。在如此大的應變率變化情況下,如果采用自由膨脹數(shù)據(jù)窗口中心處的應變率作為平均值,是不合適的。
通過回收樣品可以看出,如圖5所示,實驗1中,圓孔經歷大變形之后,局部萌生裂紋,裂紋微小的擴展(約0.5 mm)后,裂紋滯止;實驗2與實驗3變形較大,但均未完全破壞;實驗4中樣品完全破碎。
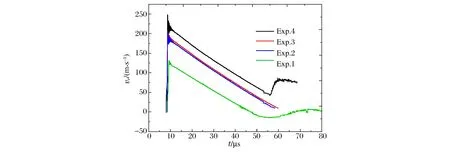
圖4 20鋼柱殼徑向速度曲線Fig.4 Velocity along radial direction of 20 steel expanding cylinder

圖5 20鋼實驗1~4回收樣品Fig.5 Recovered samples of 20 steel experiments
高速攝影采用前照明,每幅之間間隔2 μs。圖6給出了實驗3高速攝影圖像,可以清晰地看到預置圓孔局域的膨脹變形,裂紋萌生、擴展及止裂等現(xiàn)象。

圖6 實驗3膨脹斷裂高速分幅圖像Fig.6 High-speed image frames of expanding and fracture
在裝置的動作過程中,炸藥在中心線起爆之后約4 μs沖擊波傳遞至試樣,由實驗3高速攝影圖像可以看出,在20 μs時,裂紋萌生,隨后裂紋擴展,當擴展至一定長度后裂紋止裂。隨著裂紋的擴展,所發(fā)射的Mott卸載波將會繞射至速度的測試點,下面我們將估計Mott卸載波對速度測試的影響。

依據(jù)公式(1)~(2)可以得到實驗1~4的環(huán)向應力與環(huán)向應變隨時間的變化關系,再由公式(4)、(7)可以獲得等效塑性應力應變關系,如圖7(a)所示。需要注意的是,此處的應力應變關系曲線上不同點的應變率不同,這種數(shù)據(jù)對于建模而言,使用比較困難。

圖7 應力應變曲線及恒定應變率數(shù)據(jù)點分布Fig.7 Curve of stress vs. strain and distribution of constant strain rate dates
本輪20鋼實驗1~4的應變率變化范圍分別為6.14×103~0 s-1、8.62×103~8.1×102s-1、8.76×103~8.1×102s-1、1.01×104~2.6×103s-1,其公共應變率范圍為6.14×103~2.6×103s-1。為了獲得恒定應變率下的流動應力應變關系,原則上可以選擇4發(fā)實驗公共應變率范圍內的任意數(shù)據(jù)點進行處理。不失一般性,選擇5.5×103、5.0×103、4.5×103、4.0×103、3.5×103、3.0×103s-1等6組應變率點,盡可能均勻覆蓋公共應變率范圍,如圖7(b)所示。可以看出,隨著應變率的線性增加,流動應力準線性增加,實驗數(shù)據(jù)展現(xiàn)出明顯的應變率效應。
標準的JC本構方程為
(8)
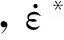
(9)
并采用修正后的JC本構方程擬合6組應變率點,如圖8所示。

圖8 恒定應變率下的應力應變曲線Fig.8 Stress-strain curves at constant strain rates
最終確定20鋼在拉伸加載下應變率為3.0×103~5.5×103s-1時的JC本構參數(shù)為:A=0.25 GPa、B=0.54 GPa、n=0.31、c=0.002、d=5×10-5。從圖8可以看出,采用應變率修正后的JC本構方程,可以更好的擬合20鋼柱殼在拉伸加載下的寬應變率范圍下的實驗結果。需要說明的是,公式(9)是一個單調遞增函數(shù),在應變較大時無法描述應變軟化特征。
上述數(shù)據(jù)處理方法,通過一組不同載荷強度下膨脹柱殼的實驗數(shù)據(jù),在其公共的應變率范圍內選擇了6組應變率下的應力應變數(shù)據(jù),通過擬合,獲得了恒定應變率下的20鋼柱殼拉伸應力應變關系,這種處理手段避免了膨脹環(huán)、膨脹柱殼實驗中應變率變化范圍過大的缺陷。另一方面也發(fā)現(xiàn),利用膨脹環(huán)、柱殼實驗裝置研究材料的拉伸應力應變關系,僅通過單次實驗是無法準確獲得某一恒定應變率下的本構關系。這就要求在相同的裝置結構上,獲得載荷強度存在一定差異的一組數(shù)據(jù),再通過后期的數(shù)據(jù)處理得到恒定應變率下的本構關系。雖然為了獲得恒定應變率下的本構關系需要的實驗數(shù)量較多,但回報卻是非常豐厚的,理論上可以獲得對應應變率變化范圍內任意恒定應變率下的應力應變關系。
4 結 論
針對膨脹環(huán)、柱殼實驗中非恒定應變率現(xiàn)象,從理論和實驗兩方面進行研究,初步得到如下結論:
(1)分析了膨脹柱殼非恒定應變率的來源,指出這一現(xiàn)象是實驗基本原理導致,在實驗中無法避免;
(2)設計了預置中心圓孔的金屬柱殼實驗,可以有效避免隨機裂紋對速度測試的影響;
(3)采用不同載荷下相同結構的膨脹柱殼實驗,建立了獲得恒定應變率下本構方程的方法,獲得了20鋼柱殼在恒定應變率(3.0×103~5.5×103s-1)下的本構方程。
感謝張振濤、金山、陳浩玉在實驗開展中的幫助,感謝劉明濤、范誠在本文撰寫過程中的建議。
[1] Johnson P C, Stein B A, Davis R S. Measurement of dynamic plastic flow properties under uniform stress[C]∥Symposium on the Dynamic Behavior of Materials. ASTM Special Publication, 1963:195-198.
[2] Hiroe T, Matsuo H, Fujiwara K, et al. Dynamic behavior of materials induced by explosive loadings initiated using wire explosion techniques[J]. Journal of Materials Processing Technology, 1999,85(1/3):56-59.
[3] Hiroe T, Fujiwara K, Hata H, et al. Deformation and fragmentation behavior of exploded metal cylinders and the effects of wall materials, configuration, explosive energy and initiated locations[J]. International Journal of Impact Engineering, 2008,35(12):1578-1586.
[4] 湯鐵鋼,李慶忠,陳永濤,等.實現(xiàn)材料高應變率拉伸加載的爆炸膨脹環(huán)技術[J].爆炸與沖擊,2009,29(5):546-549. Tang Tiegang, Li Qingzhong, Chen Yongtao, et al. An improved technique for dynamic tension of metal ring by explosive loading[J]. Explosion and Shock Waves, 2009,29(5):546-549.
[5] 湯鐵鋼,桂毓林,李慶忠,等.爆炸膨脹環(huán)實驗數(shù)據(jù)處理方法討論[J].爆炸與沖擊,2010,30(5):505-510. Tang Tiegang, Gui Yulin, Li Qingzhong, et al. A discussion of data processing techniques for expanding ring tests[J]. Explosion and Shock Waves, 2010,30(5):505-510.
[6] 湯鐵鋼,李慶忠,劉倉理,等.爆炸膨脹環(huán)的截面尺寸效應[J].爆炸與沖擊,2010,30(1):39-44. Tang Tiegang, Li Qingzhong, Liu Cangli, et al. Size effects of expanding ring by explosive loading[J]. Explosion and Shock Waves, 2010,30(1):39-44.
[7] 湯鐵鋼,李慶忠,陳永濤,等.爆炸膨脹環(huán)一維應力假定的分析與討論[J].爆炸與沖擊,2010,30(6):577-582. Tang Tiegang, Li Qingzhong, Chen Yongtao, et al. Discussion about one-dimensional stress presume for explosion expanding ring test[J]. Explosion and Shock Waves, 2010,30(6):577-582.
[8] Warnes R H, Karpp R R, Follansbee P S. The freely expanding ring test-A test to determine material strength at high strain rates[J]. Journal De Physiques IV, 1985,46(C5):583-590.
[9] 宋力,胡時勝.SHPB測試中的均勻性問題及恒應變率[J].爆炸與沖擊,2005,25(3):207-216. Song Li, Hu Shisheng. Stress uniformity and constant strain rate in SHPB test[J]. Explosion and Shock Waves, 2005,25(3):207-216.
[10] 奧爾連科.爆炸物理學[M].孫承緯,譯.北京:科學出版社,2011:822-825.
[11] Grady D E, Kipp M E. The growth of unstable thermoplastic shear with application to steady-wave shock compression in solids[J]. Journal of the Mechanics and Physics of Solids, 1987,35(1):95-119.
[12] Grady D E. Fragmentation of Rings and Shells: The Legacy of N. F. Mott[M]. New York: Springer, 2006.
[13] 劉旭紅,黃西成,陳裕澤,等.強動載荷下金屬材料塑性變形本構模型評述[J].力學進展,2007,37(3):361-374. Liu Xuhong, Huang Xicheng, Cheng Yuze, et al. A review on constitutive models for plastic deformation of metal materials under dynamic loadings[J]. Advances in Mechanics, 2007,37(3):361-374.
(責任編輯 曾月蓉)
Constitutive equation of expanding cylindrical shell at constant strain rate
Guo Zhaoliang1, Ren Guowu1, Zhang Shiwen1,Tang Tiegang1, Liu Cangli2
(1.InstituteofFluidPhysics,ChinaAcademyofEngineeringPhysics,Mianyang621999,Sichuan,China;2.ChinaAcademyofEngineeringPhysics,Mianyang621999,Sichuan,China)
In this work, taking into account of the interference of random cracks in the expansion process, we designed a cylindrical sample made with a preset hole. Then, using the Doppler pins system (DPS), we obtained some better curves for the cylinder’s radial speed histories. Based on the non-constant strain rate phenomena in the expanding ring and expanding cylinder experiments, we conducted experiments and studied a method for obtaining constitutive equation at constant strain rate. The improved constitutive equation method was used to obtain the modified constitutive equation at constant strain rate for 20 steel.
solid mechanics; constitutive equation; Doppler pins system(DPS); expanding cylindrical shell; constant strain rate
10.11883/1001-1455(2016)05-0583-07
2015-01-12; < class="emphasis_bold">修回日期:2015-05-06
2015-05-06
國家自然科學基金項目(11172279,11102191)
郭昭亮(1984— ),男,博士研究生,助理研究員,glogos@caep.cn。
O347.3 <國標學科代碼:13015 class="emphasis_bold"> 國標學科代碼:13015 文獻標志碼:A國標學科代碼:13015
A

