起伏濕氣管路持液率和壓降計算模型

王文光，顏慧慧，曲兆光，劉春雨，萬宇飛

1.中海石油（中國）有限公司天津分公司，天津 300452

2.中石化天津石油分公司，天津 300100

起伏濕氣管路持液率和壓降計算模型

王文光1，顏慧慧2，曲兆光1，劉春雨1，萬宇飛1

1.中海石油（中國）有限公司天津分公司，天津 300452

2.中石化天津石油分公司，天津 300100

濕氣集輸管道在天然氣開發中發揮著重要作用，如果濕氣管道內存在積液，會導致能耗增加、腐蝕加劇和生成水合物等問題，但目前尚沒有一個瞬態兩相流模型能夠準確地計算起伏濕氣管道中的積液和壓降規律。在已有的兩相流雙流體模型基礎上，基于連續性方程和動量方程，建立了一種新的適用于起伏管路的瞬態兩相流理論模型，并利用數值方法通過編制MATLAB程序實現對起伏濕氣管道中持液率及壓降等的計算。利用普光氣田現場濕氣集輸管道的運行數據對模型進行了驗證，并與多相流軟件OLGA的模擬計算結果進行了對比。驗證結果證明所建立的模型計算精度較高，持液率和壓降的相對誤差分別為±15%、±5.5%，可以應用于起伏濕氣管道兩相流的模擬。

起伏濕氣管路；瞬態兩相流模型；持液率；壓降

濕氣集輸管道中如果存在積液會導致能耗增加，腐蝕加劇，同時還存在生成水合物的風險[1]；而在復雜的地形條件下，管道的起伏對管內兩相流流型、氣液相相間作用有很大的影響，從而導致積液規律等問題更加復雜化。因此，探索起伏濕氣管道內的持液率和壓降計算方法，對預防管道積液，提高管道輸送效率和安全性，具有十分重要的意義[2]。

近年來許多學者對起伏管道內的兩相流機理和流動規律進行了實驗及理論研究，提出了若干適用于起伏或者傾斜管路的兩相流理論模型。

1991年，Wood提出一種適用于起伏凝析氣管道的機理模型[3]，該模型以實驗為基礎，是一種一維準穩態模型。模型可以計算出能夠帶走管道低洼處積液的臨界氣體速度、最大穩定段塞長度以及初始段塞特性。Zheng通過研究總結了兩相流管路的起伏對流動的影響[4]，并針對單個起伏管道提出了一種段塞跟蹤的理論模型[5]，研究了單個起伏管道中段塞的流動特性。1995年，Henau與Raithby提出了一種適用于多起伏管道的段塞流模型[6]，提出了關于阻力系數和虛擬質量力的新關系式，并利用實驗進行了驗證。

宋立群、李玉星針對復雜地形條件下的低含液率管道[7]，提出了穩態的水力計算模型，給出了凹面濕壁分數、摩擦因子等參數的計算式。喻西崇等人針對起伏管道對多個持液率計算相關式進行了比較[8]，包括Eaton相關式、Dukler II相關式、BB相關式等，給出了各相關式適用的傾角范圍。

國內外對起伏管路兩相流的研究現狀表明，管道起伏對氣液兩相流流型、氣液相分布和管道壓降等具有十分顯著的影響，但目前尚沒有一個較好的模型能夠準確地預測復雜多起伏濕氣管道內的流動特性，且多數兩相流模型是建立在穩態工況條件之上的，對起伏管道內瞬態模型的研究較少。

1 瞬態兩相流理論模型

為實現對起伏濕氣管路中持液率和壓降等參數的計算，本文將結合已有的雙流體模型，針對起伏管路中常見的流型，選擇合適的閉合關系式，建立適用于絕熱條件下的瞬態氣液兩相流的理論模型。

1.1 基本方程

兩相流瞬態模型的建立以流體力學基本守恒方程為基礎，作出以下假設[9]：

（1）認為管道處于絕熱條件下，可忽略能量方程。

（2）管道內氣體可以近似作為理想氣體處理。

（3）不考慮相變與相間傳質。

根據以上假設，兩相流中k相（k=g表示氣相、k=l表示液相）的連續性方程和動量方程分別為：

式中：A為管道截面積，m2；t為時間，s；αk為k相占管道截面積的比例；ρk為k相密度，kg/m3；uk為k相速度，m/s；S′mk為單位長度上的質量源項，kg/（s·m）；Pk為k相壓力，Pa；x為長度，m；Fkx為單位質量力，N/kg；Tkw為k相與管道壁面通過剪切力產生的單位面積動能交換，N/m；Tki為k相在相界面處的單位面積動能交換，N/m；x為x位置處的單位向量；k為k相界面單位向量，l=-g；l、g分別為氣、液相界面單位向量；τkw為k相壁面剪切應力，N/m2；ΔPki為k相在相界面處的壓力差，Pa；P′ki為k相由于相對速度導致的壓力波動，Pa；τki為k相在相界面處的剪切應力，N/m2；Pgi、Pli為氣、液相局部界面壓力，Pa；τgi、τli分別為氣、液相在相界面處的剪切應力，N/m2；σ為相界面表面張力，N/m；Ri為相界面平均曲率半徑，m。

1.2 閉合方程

1.2.1 分層流

為推導分層流閉合方程，需要作出以下假設（見圖1）：第一，假設分層流中氣液界面為水平界面。第二，假設氣液相界面的曲率半徑足夠大，表面張力作用可以忽略。第三，忽略相界面壓力波動P′ki。

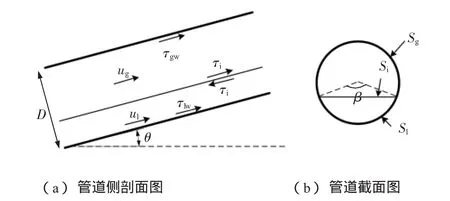
圖1 分層流氣液相分布

可以得出分層流的閉合方程為[9]：

式中：P′gi為由于相對速度導致的氣相壓力波動，Pa；ΔPgi、ΔPli分別為氣、液相在相界面處的壓力差，Pa；ρg、ρl分別為氣、液相密度，kg/m3；g為重力加速度，取9.8 m/s2；αg、αl分別為氣、液相占管道截面積的比例。

假設k相與壁面的剪切力沿Ckw（k相在截面內與管壁的交線，m）不變，則k相與壁面的單位面積動能交換可以寫作：

式中：Sk為k相的濕周，m；fk為k相壁面摩擦系數。

k相壁面摩擦系數fk的計算公式[10]：

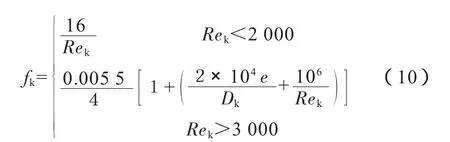
當2 000≤Rek≤3 000時，取上述兩者中計算值較大者。

式中：e為管壁粗糙度，m；Rek為k相雷諾數；Dk為k相水力直徑，m。

氣液界面處的單位面積動能交換等于界面處的剪切應力：

式中：Tgi、Tli分別為氣、液相在相界面處的單位面積動能交換，N/m；fi為界面摩擦系數；ur為相對速度，m/s，ur=ug-ul，當ug＞ul，氣相產生壓力降，反之液相產生壓力降。

界面摩擦系數fi選用Andritsos[11]所提出的計算公式：

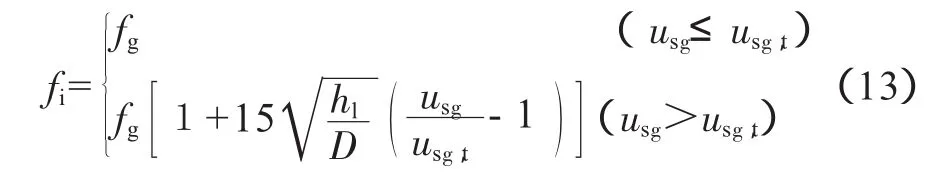
式中：fg為氣相壁面摩擦系數；usg為氣相表觀速度，m/s；usg，t為臨界氣相表觀速度，m/s；hl為穩態分層流液膜厚度，m。

式中：P為系統壓力，Pa。

1.2.2 環狀流

環狀流的閉合方程為：

由于認為環狀流的液膜很薄，所以可以認為相平均壓力[Pk]（Pa）等于界面平均壓力Pi（Pa），故可得：

環狀流中壁面摩擦系數與分層流公式相同，即公式（9）、（11）。

界面摩擦系數fi按照下面的公式計算[12]：

式中：Reg為氣相雷諾數；δ為分層流液膜厚度，m；μg為氣相動力黏度，Pa·s。

1.2.3 分散流

為了便于推導，方程中使用下標d表示分散相，下標c表示連續相。

假設管道截面內分散相的壓力等于連續相的壓力，即：

式中：Pc、Pd分別為連續相、分散相平均壓力，Pa。

根據上述假設，氣液界面動量方程可以化簡為：

式中：Tci、Tdi分別為連續相、分散相在相界面處的單位面積動能交換，N/m。

Stuhmiller給出了分散流界面處Tci的表達式：

式中：CD為阻力系數，按照文獻[13]中的方法計算；ρc為連續相密度，kg/m3；ur為相對速度，m/s，ur= ud-uc；uc、ud分別為連續相、分散相速度，m/s；αc、αd分別為連續相、分散相占管道截面積的比例；r為分散相半徑，m；CVM為虛擬質量力系數；εc為連續相濕壁系數，對于均勻分布的混合物，εc=αc；dur/dt為遷移導數，m/s2。

分散流壁面剪切力依然使用公式（9）計算。

1.2.4 段塞流

對于段塞流，假設一個段塞內的壓力不變，氣、液相壓力均等于截面上的平均壓力Px，即：

式中：[Pg]、[P1]分別為氣、液相平均壓力，Pa。

與分散流類似，段塞流界面動量方程可以化簡為：

參考公式（22），段塞流中Tli的表達式可以化簡為：

式中：l為段塞總長度l=ls+lf，m，；ls、lf分別為液塞和液膜段的長度，m；ur為氣相與液相之間的平均相對速度，m/s；u′r為段塞平移速度vt與液膜速度vlf之差，u′r=vt-vlf，m/s。

段塞流中，流體壁面剪切力應該分別計入液塞段和液膜段的壁面剪切力[14]，因此一個段塞內的剪切應力可以寫為：

式中：τkf、τks分別為液膜段、液塞段k相的剪切應力，N/m2；Skf、Sks為液膜段、液塞段k相濕周，m。

1.3 氣體狀態方程修正

對于壓力較高的氣田集輸管道，理想氣體的假設會帶來較大誤差，因此需要對模型進行修正。

考慮到天然氣組分較為復雜，采用BWRS方程對模型中氣體密度的計算進行修正。BWRS方程形式如式（27） 所示[15-16]：

式中：p為系統壓力，kPa；R為通用氣體常數，R= 8.314 J/（mol·K）；T為系統溫度，K；A0，B0，C0，D0，E0，a，b，c，d，α，γ為狀態方程的11個參數，具體計算方法請參考文獻[17]。

由于BWRS方程形式十分復雜，如果采用線性化、離散的處理辦法會大大增大程序的復雜程度，導致計算速度降低，因此程序中采用延時修正的方法，即先假設氣體為理想氣體（壓縮因子Z=1），計算出各點壓力后，再利用計算出的壓力值計算氣體密度和壓縮因子，然后在循環過程中不斷更新壓縮因子，從而達到對氣體密度的修正。

2 現場起伏濕氣管道數據驗證

普光氣田采用濕氣集輸系統，管道內氣、液相并存[18]，由于受地形影響，管道起伏比較劇烈，管道內兩相流動較為復雜，因此探究管道內氣液兩相流流動規律對管路的優化設計和經濟、安全運行具有十分重要的意義。

圖2為普光氣田P201集氣站至集氣末站的管道高程圖[19]，從圖中可以看出，管道起伏劇烈，管道最大的傾角可以達到47.8°。

圖2 普光氣田P201-集氣末站管道高程

為了驗證本文模型的可靠性，利用該管道的現場運行數據對模型的計算結果進行驗證，同時與瞬態多相流軟件OLGA的計算結果進行對比，結果見表1和表2。

表1 持液率計算結果與測量值對比

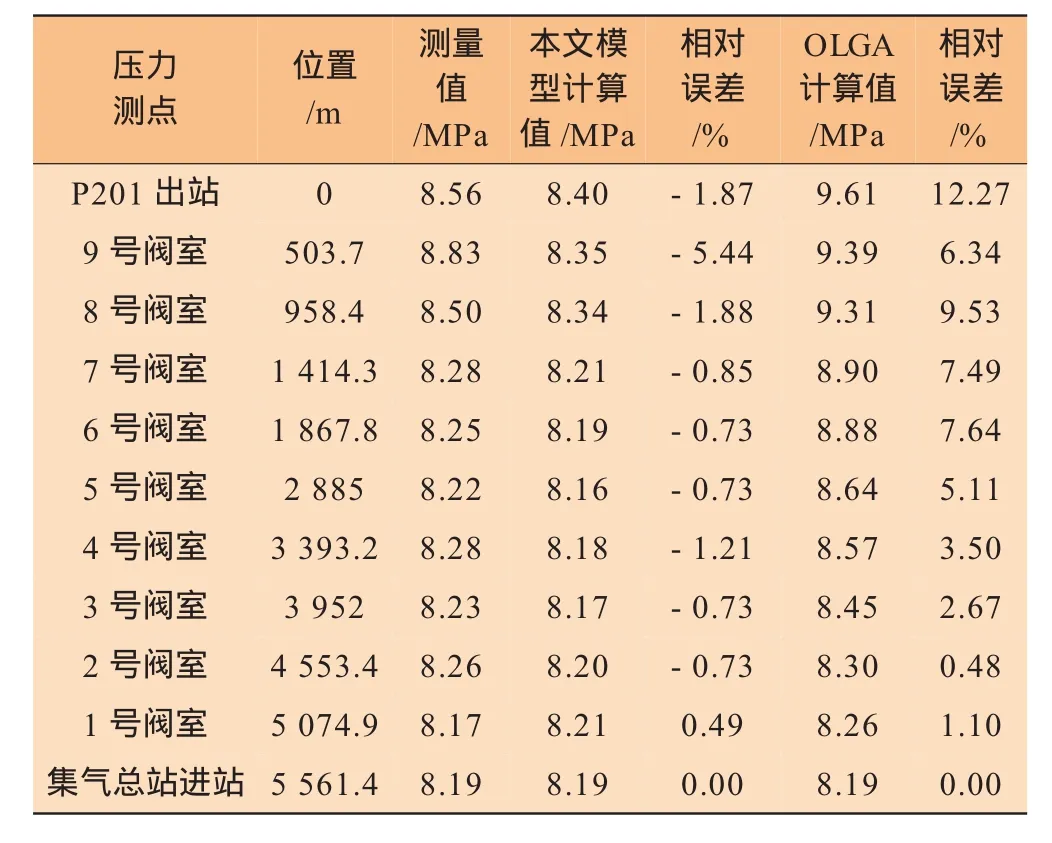
表2 管道壓力分布計算結果與測量值對比

從表1管道持液率的計算結果分析，本文模型和OLGA軟件對管道持液率的計算結果誤差均在±15%以內，能夠很好地預測管道內液相分布規律。

從表2中可以看出，OLGA軟件計算的管道壓力結果普遍偏大，原因是OLGA對流型的判斷準確性較差，由于在較大范圍內存在段塞流，因此導致管道壓力升高。由于引入了BWRS方程對氣體密度進行修正，本文模型對管道壓力的計算精度明顯提高，相對誤差均在±5.5%以內。

3 結論

與現場多起伏濕氣管道實際運行數據的對比表明，本文的瞬態兩相流模型能夠很好地模擬起伏濕氣管道內的兩相流流動，其中，采用本文模型計算持液率的計算精度為±15%，壓力計算精度可達±5.5%，與OLGA計算結果相比，本文模型對壓力的計算精度更高，兩者對持液率的計算精度相近。

[1]張欽杰.氣液兩相流管道振動機理研究[D].青島：中國石油大學（華東），2009.

[2]周良勝.復雜地表條件下天然氣集輸管線積液規律研究 [D].青島：中國石油大學（華東），2009.

[3]WOOD D.Mechanistic modeling of terrain-induced slugs in gas/condensate lines[C]//Proceedings of BHRG Multiphase Conference.Cannes，France：BHRG，1991.

[4]ZHENG G.Two-phase slug flow in hilly terrain pipelines[D]. Tulsa，US：University of Tulsa，1991.

[5]ZHENG G，BRILL J P，TAITEL Y.Slug flow behavior in a hilly terrain pipeline[J].International journal of multiphase flow，1994，20（1）：63-79.

[6]De HENAU V，RAITHBY G D.A transient two-fluid model for the simulation of slug flow in pipelines—I.Theory[J]. International journal of multiphase flow，1995，21（ 3）：335-349.

[7]宋立群，李玉星.復雜地形條件下氣液兩相混輸工藝水力模型建立[J].化工學報，2012，62（12）：3 361-3 366.

[8]喻西崇，趙金洲，馮叔初.起伏多相流管路持液率計算方法研究[J].西南石油學院學報，2000，22（3）：94-97.

[9]DE HENAU V.A study of terrain-inducedsluggingin two-phase flow pipelines[D].Waterloo，Canada：University of Waterloo，1992.

[10]BENDIKSEN K，MAINES D，MOE R，et al.The Dynamic Two-Fluid Model OLGA：Theory and Application[J].Spe Production Engineering，1991，6（2）：171-180.

[11]ANDRITSOS N，HANRATTY T J.Influence of interfacial waves in stratified gas-liquid flows[J].AIChE Journal，1987，33（3）：444-454.

[12]FORE L B，BEUS S G，BAUER R C.Interfacial friction in gas-liquid annular flow：analogies to full and transition roughness [J].International Journal of Multiphase Flow，2000，26（11）：1 755-1 769.

[13]ISHII M，MISHIMA K.Two-fluid model and hydrodynamic constitutive relations[J].Nuclear Engineering and Design，1984，82（84）：107-126.

[14]曹學文，周鵬.油氣水三相段塞流的壓降研究[C]//中國工程熱物理學會多相流學術會議論文集.重慶：中國工程熱物理學會，2006.

[15]STARLING KE，HAN M S.Thermo data refined for LPG--14. Mixtures [J].Hydrocarbon Processing，1972，51（ 5）：129-132.

[16]苑偉民.修改的BWRS狀態方程[J].石油工程建設，2012，38（6）：9-12.

[17]吳玉國，陳保東.BWRS方程在天然氣物性計算中的應用[J].油氣儲運，2003，22（10）：16-21.

[18]李玉浩，曹學文，雷毅，等.基于超聲回波特性的濕氣集輸管線積液檢測技術[J].石油學報，2013，34（6）：1 200-1 205.

[19]李玉浩，曹學文，梁法春，等.多起伏濕氣集輸管線工藝計算方法優選[J].天然氣工業，2013，33（8）：114-118.

Calculation Model of L iquid Holdup and Pressure Drop in Undulating Wet-gas Gathering Pipeline

WANG Wenguang1，YAN Huihui2，QU Zhaoguang1，LIU Chunyu1，WAN Yufei1
1.CNOOC Tianjin Company，Tianjin 300452，China
2.Sinopec Tianjin Company，Tianjin 300100，China

Wet-gas gathering pipeline plays an important role in natural gas development.Liquid accumulation in the wet-gas pipeline will result in higher energy consumption，corrosion and more hydrates.However，the prediction of the flow behavior in the undulating wet-gas pipeline is difficult，thus no accurate modelis available now.Based on the existing two-phase flow model，a transient two-phase flow model applicable for the undulating wet-gas pipeline is developed in this paper.AMATLAB code is developed and applied to simulate the flow in wet-gas pipeline.In order to testify the accuracy of the model，the liquid holdup and pressure drop of the wet-gas gathering pipeline in Puguang Gas Field are calculated with the errors of±15%and±5.5%respectively.The results are also compared with those calculated by OLGA，which shows the modelcan be applied to simulate the two-phase flow in undulating wet-gas gathering pipeline.

undulating wet-gas pipeline；transient two-phase flow model；liquid holdup；pressure drop

10.3969/j.issn.1001-2206.2016.06.001

王文光（1989-），男，山東濱州人，助理工程師，2015年畢業于中國石油大學（華東）油氣儲運工程專業，主要從事海上油氣田開發前期研究、管道安全流動保障工作。Email：wangwg17@cnooc.com.cn

2016-05-24