基于四叉樹原理的多波段遙感影像區域合并算法

劉耀林，丁名時

(武漢大學資源與環境科學學院，湖北 武漢 430079)

?

基于四叉樹原理的多波段遙感影像區域合并算法

劉耀林，丁名時

(武漢大學資源與環境科學學院，湖北 武漢 430079)

A Region-merging Algorithm toward Multiband Remote Sensing Image Based on the Quadtree Principle

LIU Yaolin，DING Mingshi

摘要：隨著計算機技術的發展，通過處理分析遙感影像數據獲取信息達到科研或工程應用目的已成為一種普遍的模式。遙感影像數據在包含豐富信息量的同時，其自身的海量特性也逐漸成為制約其應用的障礙之一。在諸多關于遙感影像壓縮合并方法的研究中，四叉樹原理一直是一個重點研究方向。但傳統的四叉樹算法在處理遙感影像過程中總會存在過度分割現象；而且以往的相關研究中，總是針對單一波段影像進行處理，其應用價值會有一定的局限性。針對這兩點不足，本文提出并實現了一種基于四叉樹原理的多波段遙感影像合并算法，并通過試驗進行了驗證，與傳統的四叉樹方法相比，其在壓縮比方面平均可以提高50%以上，且在壓縮精度方面也取得了良好的效果。

關鍵詞：四叉樹；區域合并；多波段；屬性空間

遙感影像是信息的重要載體。近年來，隨著計算機技術的發展，通過對遙感影像的分析處理，進而獲得相關信息已成為諸多科研及工程領域研究、應用的一種重要模式[1-2],但其數據量龐大且具有一定冗余度，成為制約其應用的一大障礙。因此，一直以來，關于遙感影像數據的壓縮編碼及空間對象合并技術都是相關領域研究和關注的重點。

在諸多關于遙感影像壓縮合并方法的研究中，四叉樹原理以其優良的表現和簡潔的編碼過程一直以來都是一個重點的研究方向，而且相關的研究成果較多[3-8]。

關于四叉樹原理的壓縮研究主要分為兩個研究重點：一個研究重點是研究在一定誤差范圍內，提高數據的壓縮程度。這個問題上比較典型的有3個子方向：一是各種自適應判別謂詞的改進，如倪林提出一種自適應四叉樹分割處理方法，有效提高了遙感圖像的壓縮比[4]；二是引入新的理論對分割結果進行優化[6]；三是分割形狀的改進[5]。另一個研究重點是研究如何提高壓縮過程效率。這個問題的主要研究內容是將四叉樹自上而下的遞歸構建過程改為自底至上的線性編碼過程，以及對這種線性編碼過程進行優化[3]。

諸多研究工作者在這兩個問題的研究上取得了顯著的成果。但其中也有一些尚待研究的問題，如在諸多相關研究文獻中，基于四叉樹原理的遙感影像處理研究大都是基于單一波段的灰度圖像。而在對于遙感影像數據的分析研究中大都是基于多個波段的影像進行的。另外，四叉樹算法由于其原理的特性，會在數據分塊壓縮過程中產生過度分割現象，但在相關文獻中，對于這個問題的解決卻很少涉及。

本文針對以往研究中存在的這兩點待改進之處，提出一種基于四叉樹原理的多波段遙感圖像區域合并有損壓縮算法。該算法能夠將多波段的遙感圖像數據進行區域合并，經試驗驗證，比傳統的四叉樹算法具有更高的壓縮比。

一、多波段遙感圖像的區域合并算法

1. 經典四叉樹算法原理

在介紹本文算法之前，首先來簡要介紹一下經典的四叉樹算法原理。四叉樹是一種樹形數據結構，它的每個節點下可以有4個子節點或沒有子節點(如圖1所示)。

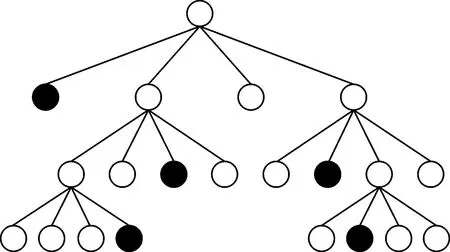
圖1　四叉樹示意圖

在構建圖像四叉樹編碼的過程中，算法首先要設立一個判斷謂詞，以對節點區域是否需要繼續分割進行判斷；而后將原始數據作為根節點，判斷節點是否可以繼續分割，若滿足繼續分割條件，則將節點區域分為4組相同的象限；而后對4組象限繼續迭代執行判斷分割過程，直到所分節點區域不滿足繼續分割條件而終止(如圖2所示)。

圖2　四叉樹圖像壓縮示意圖

從算法原理上看，四叉樹的構造過程本質是遞歸構造，這在算法實現的過程中具有編碼簡潔、易于理解等優點。

下面本文將對所提出的改進算法進行詳細的闡述。

2. 針對多波段圖像的判別謂詞設計

通過上一節關于經典四叉樹算法原理的介紹可以看出，在對數據進行四叉樹處理的過程中，首先就是要確定區域可分割條件，即判別謂詞。對于單一波段遙感影像，其可用以下形式表示

式中，fij為坐標為(i，j)的像元的灰度值。這種情況下，四叉樹的判別謂詞基本上都是對區域灰度值的一些統計信息的一些判別。而多波段圖像中，每一個像元在每個波段上都有一個對應的屬性值，這使得對其可分割條件的確定造成了一定的困難。

在此，引入“屬性空間”這一概念，即將任一像元所對應的各波段的屬性值看作該像元所對應的屬性向量，對于k個波段的遙感影像可表示為

式中，像元(i，j)的屬性為一個k維向量，向量的每一維分量對應著該像元的一個波段的屬性值。

引入屬性空間概念后，一個區域內的像元屬性即可看作是屬性空間中分布的一些離散點。由灰度圖像處理中的判別謂詞設計方式很容易聯想到，此時，對于判別謂詞可以設計為針對這些屬性點的某些統計信息的判別。

在對于灰度圖像的四叉樹分解中，比較常用的一種判別方案是對區域灰度級差的閾值判別，即若區域內灰度最大值與最小值的差大于預設閾值，即判定此區域為非同質區域，需要繼續對其進行分解；否則判定為同質區域，保留區域為四叉樹的一個葉節點。在“屬性空間”的統一表達之下，這種灰度值的級差可以用區域內屬性點的最遠點距代替。因此，本文所采用的判別謂詞為區域內屬性點中最遠點對的絕對值距離與預設閾值的大小比較，若最遠點距大于閾值，則區域需要繼續分割；若小于閾值，則保留區域為四叉樹的一個葉節點。即對于區域Fk，通過判斷與預設閾值的大小關系，來判定區域是否繼續分割。其中，p-m≥0，q-n≥0，且p-m和q-n不同時為0。

確定了判別條件之后，需要設計一套具有可行性的具體方案。由于遙感數據的海量特性，在對其中某個區域進行最遠點距計算的過程中不可能采用暴力搜索的方式。本文采取的辦法是首先求出區域屬性點的凸包點集，屬性點中的最遠點對顯然會產生在凸包點集內。因此，只需要計算凸包點集中最遠點對的距離，即可求得區域屬性點中的最遠點對距離。

在求區域屬性點凸包點集的過程中，有一點需要注意，即對于多波段的遙感影像數據，其屬性點都是多維的，而某區域內屬性點在屬性空間中的分布形態維度有可能會與屬性空間維度不同，如三維空間中的共面分布或共線分布的離散點。而產生最遠點距的凸包點集顯然是針對于分布形態下的凸包點集，且對于不同維度的離散點數據，求取凸包點集的過程是有所差別的。因此，在求區域屬性點凸包點集之前，需要首先對屬性點的分布形態進行確定，而后再針對分布形態，求其凸包點集，并進行最遠點距的計算。

對于區域屬性點分布形態的確定，本文采用如下策略，以三維數據為例，某區域內的屬性點可以表示為

式中，矩陣中每一行代表一個屬性點數據，每一列分別代表不同波段。對于屬性點集P，首先將其中第一個點移至原點，其余點作相應移動，去掉原點后，得到新點集P′，如下所示

由相關知識易知，原始點集的分布形態維度與新點集矩陣P′的秩相同，即若原始點集呈三維形態分布，則矩陣P′的秩為3；若呈二維形態分布(共面分布)，則矩陣P′的秩為2，以此類推。

因此，可以通過取矩陣P′的一個列極大線性無關組來選取對確定屬性點位置有獨立貢獻的分量。那么，就可以通過取原始點集P中的對應列分量，將原始點集投影到相應維度的空間，由選取條件保證，點集分布形態的維度與投影空間的維度必然相等。因此，可以在投影空間中求出凸包點集，再將其對應到原始點集求出屬性點的最遠點對距離。

采用以上一整套執行方案，不僅可以在多波段遙感影像區域分割條件判別過程中避免錯誤，還能夠極大限度地減少判別過程的運算量，提高程序的效率。

3. 基于四叉樹原理的區域合并算法

(1) 數據結構設計

在上文關于經典四叉樹原理的介紹中得知，四叉樹算法在處理圖像數據過程中，在具有相應優勢的同時，也存在著過度分割的現象。本文針對這種不足，設計出如圖3所示的數據結構，用于在四叉樹處理遙感數據過程中進行區域合并操作。

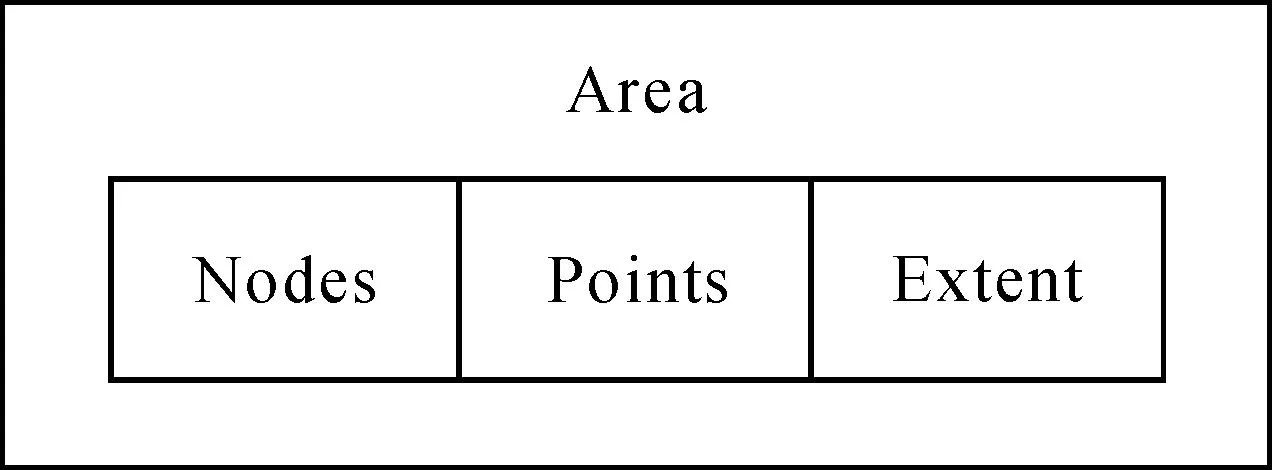
圖3　區域數據結構示意圖

該結構分為3個部分：第一部分稱為Nodes，用于存儲Area結構內每個四叉樹葉節點的上下左右四邊界在圖中的位置；第二部分稱為Points，用于存儲對應葉節點內原始像元的屬性向量；第三部分稱為Extent，用于存儲整個Area結構的四方邊界位置。

對于這種結構，本文的使用方式為在四叉樹分割構建過程中，對于不滿足可繼續分割的葉節點，首先將其按Area結構進行存儲。由于經典的四叉樹構建為一種自頂至下的迭代過程，因此在其分割完成之后，必然會存在一個自底至上的返回值過程，其返回的值即為本次迭代區域的四叉樹編碼序列。本文正是基于這種自底至上返回過程的存在，設計出一種在返回值階段的區域合并策略。

(2) 合并方案設計

首先，對于不滿足繼續分割條件的區域，算法會自動將其按Area結構進行存儲，即在遞歸過程的最底層，算法可以獲得最基礎的Area結構對象。這些Area結構對象將會被返回到遞歸的上一層。本文所提出的區域合并過程，就是從算法接收到由下層遞歸返回的基礎Area結構開始進行的。而這種接收下層返回、合并、返回上一層的模式將一直進行到四叉樹的根節點層，以完成全部輸入數據的區域合并操作。

確定整體合并過程模式之后，本文重點介紹算法合并環節的具體執行策略。由于算法的合并環節位于四叉樹遞歸的返回值階段之前，因此，對于任意一個非葉節點，它所接收到的下層返回值都是本節點區域4個象限內已經完成合并的Area結構集合。因此，在本節點將Area結構集合返回給上層節點之前，需要完成本節點內的區域合并任務，而本節點的區域合并任務，即為橫縱兩條分界線上的Area結構的合并。

具體的合并策略如下，以橫向分界線為例。

① 獲取相關元素集合

首先，搜索Area集合中Extent上界和下界落在分界線位置的元素，會得到兩個Area結構的集合

式中，第一個集合為分界線上方，區域下邊界落在分界線上的Area結構集合；第二個集合為分界線下方，區域上邊界落在分界線上的Area結構集合。由于Area結構中可能存在多個葉節點，而不是每個葉節點都與分界線相鄰，因此，為盡可能減小計算量，需要從兩個Area集合中選出相應邊界落在分界線上的葉節點，可以得到相應的兩個葉節點的集合

式中，第一個集合為分界線上方，下邊界落在分界線上的四叉樹葉節點集合；第二個集合為分界線下方，上邊界落在分界線上的四叉樹葉節點集合。

② 合并

獲取分界線上的葉節點集合之后，分別對兩個集合中的葉節點按其節點左邊界進行集合內排序，然后從左至右對兩集合中的葉節點進行合并判斷。

合并判斷的過程如下：

a. 首先判斷兩個葉節點是否鄰接，判別的方法為判斷表達式

(LNia,left-LNjb,right)(LNia,right-LNjb,left)

與0的大小，若表達式小于等于0，則兩葉節點鄰接；否則，兩葉節點不鄰接。若兩個葉節點不相鄰，則將右邊界較小的葉節點用其右側相鄰的節點代替，繼續判斷節點相鄰；若兩節點相鄰，則進行下一步。

b. 對于相鄰葉節點，取兩個葉節點所在Area的Points部分，計算兩個Area結構的屬性點最遠點距，判斷其是否小于閾值。

若小于閾值，則證明兩個Area結構可以合并，將這兩個Area結構的ID記錄下來。記錄ID的目的是用于全部判斷完畢之后的合并操作，以及防止有相同Area的重復合并。

若最遠點距不小于閾值，證明兩個Area不滿足合并條件，則在兩個葉節點集合中，右邊界較小的節點跳過與參與本次判斷的葉節點相鄰的同Area節點，而后返回步驟1)進行節點相鄰判斷。

c. 完成全部判斷之后，按記錄的可合并Area結構對Area結構進行合并。

(3) 算法流程

綜上所述，本文所提出的多波段遙感影像的區域合并算法流程如圖4所示。

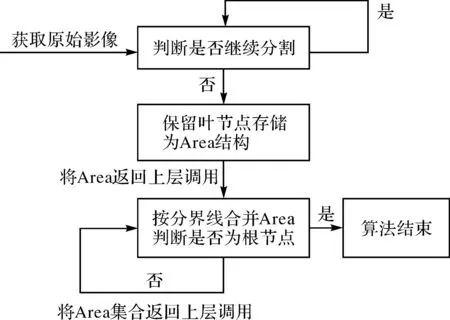
圖4　本文算法流程

如圖4所示，本文算法主要步驟如下：

1) 獲取原始影像數據，根據判別方案判斷區域是否需要分割：①若滿足分割條件，將區域四分，重復迭代步驟1)；②若不滿足分割條件，將區域保留為葉節點，并存儲為Area結構，返回給迭代上層。

2) 將接收到的下層Area集合返回值按本層分界線進行合并，并判斷是否為根節點：①若不是根節點，則將Area結構集合返回給迭代上層，重復迭代步驟2)；②若是根節點，算法結束。

二、試驗結果及分析

本文隨機選取Landsat8衛星某區域1024×1024像素尺度的多波段遙感影像數據，將本文提出的區域合并算法與傳統的四叉樹算法進行對比試驗。并通過對結果進行比較分析，闡述本文提出算法的優勢。

本文所選數據波段為2、3、4、5、6共5個波段，由于波段數量較多，本文用其自然真彩色波段來展示試驗區的直觀概況，如圖5所示。

圖5　試驗區真彩色波段遙感影像

在試驗過程中，本文所采取的預設閾值策略為用區域整體屬性點最遠點距乘以一個精度系數作為算法閾值，系數不同則算法的精度也有相應的差異。試驗所采取的具體系數為0.1、0.085、0.070、0.055、0.04、0.025、0.01共7種不同的精度。試驗結果數據對比見表1。

關于表1有幾點需要說明：

1) 本文所選區域的原始數據量為區域像元數，即1024×1024像素=1 048 576像素。

2) 本文在合并后的誤差相關值計算都是以區域內屬性均值代替區域內各像元屬性值進行的。

3) 表中的數據距平均值是將各個波段的屬性值除以波段值范圍(65 535)后的相應計算值。在各項數據中，誤差均值反映出壓縮后數據與原始數據誤差的平均程度；誤差變異系數反映出誤差分布的穩定性。

從壓縮比一項中可以看到，本文所選取的算法精度控制系數對數據的壓縮范圍基本涵蓋了從低精度壓縮到高精度壓縮的有效范圍，因此，這兩組試驗的參數選取是有意義的。

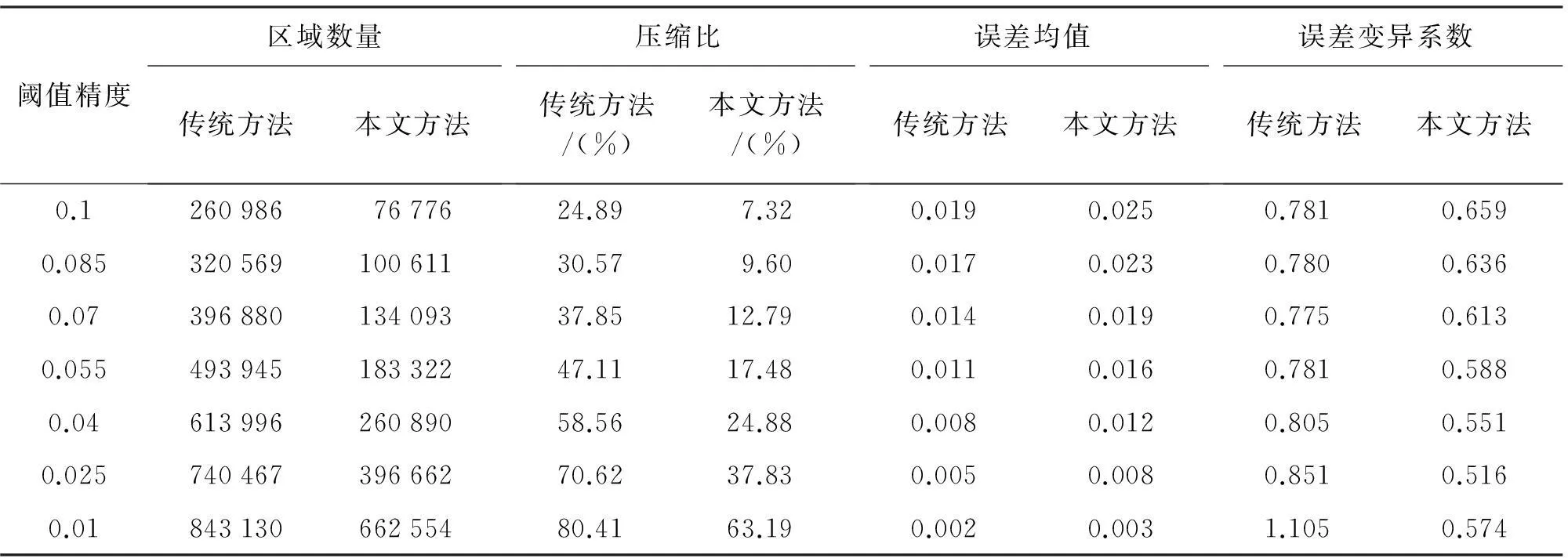
表1　傳統四叉樹試驗結果數據表

從表1可以看出，兩種算法在壓縮程度和壓縮精度方面都有不錯的表現，壓縮后的數據在概念上的數據量都有明顯的減少，而且與原始數據的誤差均值都能夠保持在一個較小的范圍內。傳統的四叉樹算法由于對數據的分割較細，因此在誤差均值方面總體上比本文算法要略好一些。但是隨著算法精度的提升，本文算法在誤差均值方面逐漸減小的同時，其與傳統四叉樹在這方面的差異也在縮小。同時，通過對誤差變異系數的對比可以看出，本文算法處理后的數據，其誤差的分布較之傳統四叉樹算法都是相對穩定的，這種誤差分布的穩定性優勢也是不可忽視的一個方面。

下面，本文將兩種算法的試驗結果相關數據繪制成圖，以便更直觀地對兩種算法的效果進行比較，如圖6—圖8所示。

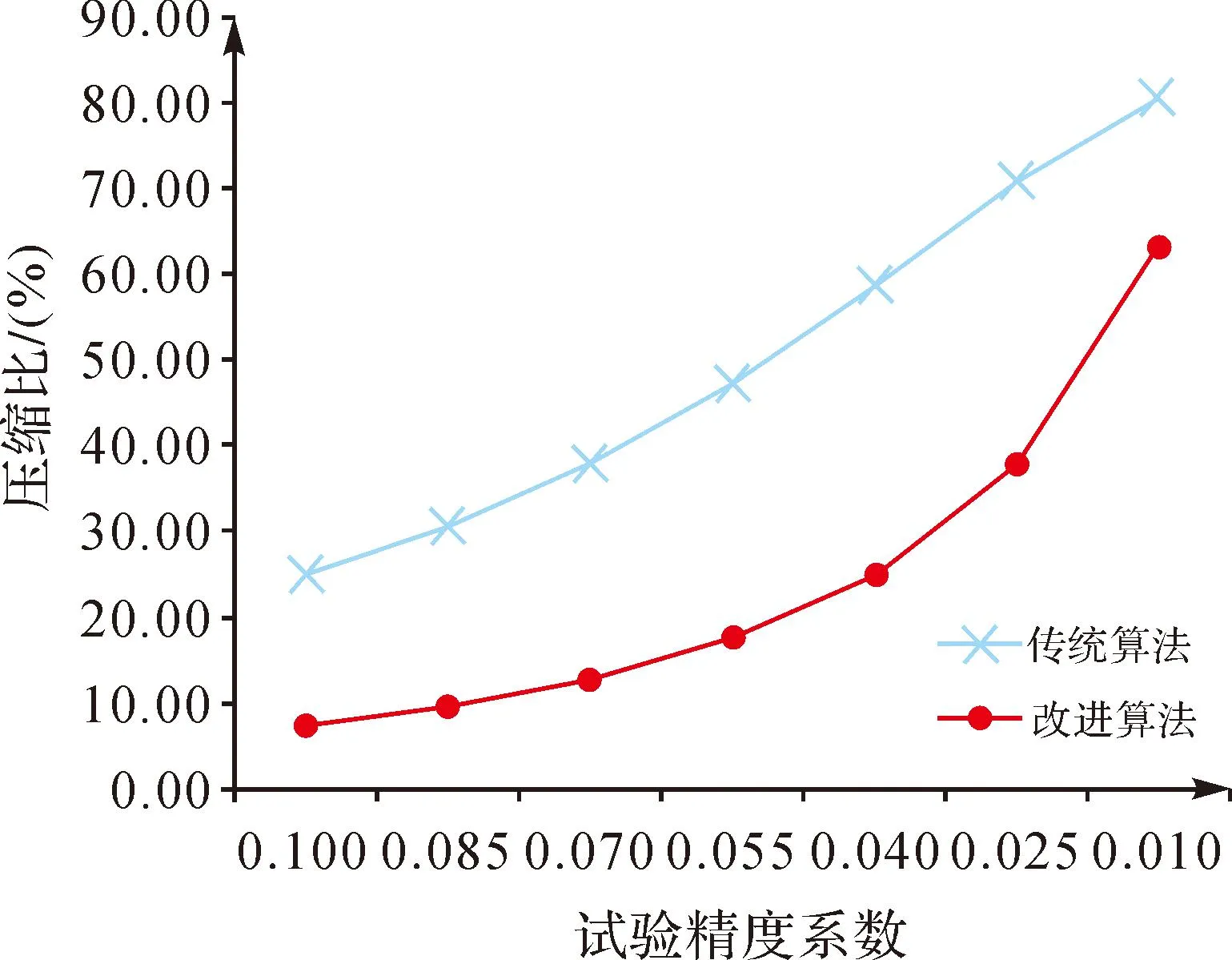
圖6　試驗結果壓縮比比較

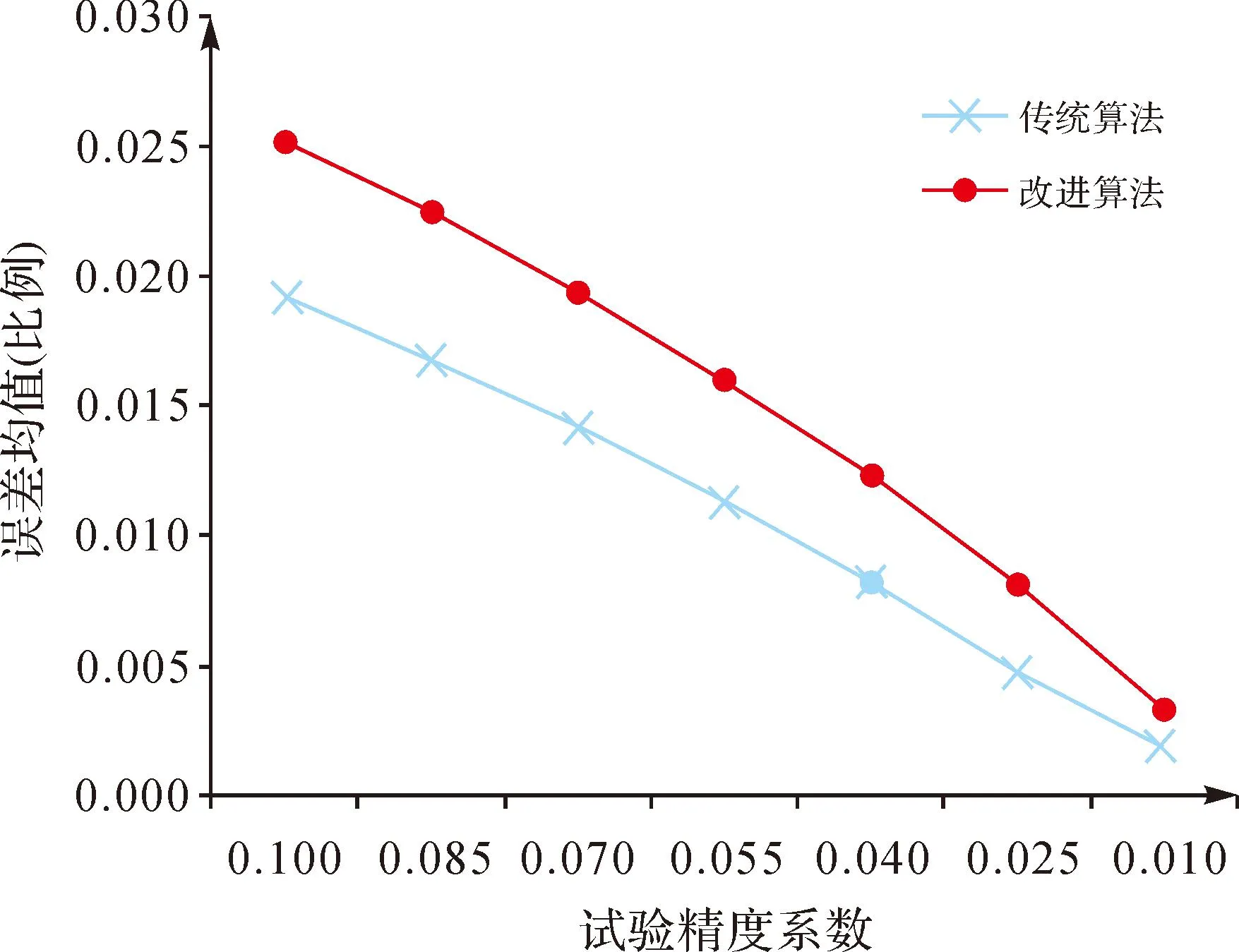
圖7　試驗結果誤差均值比較

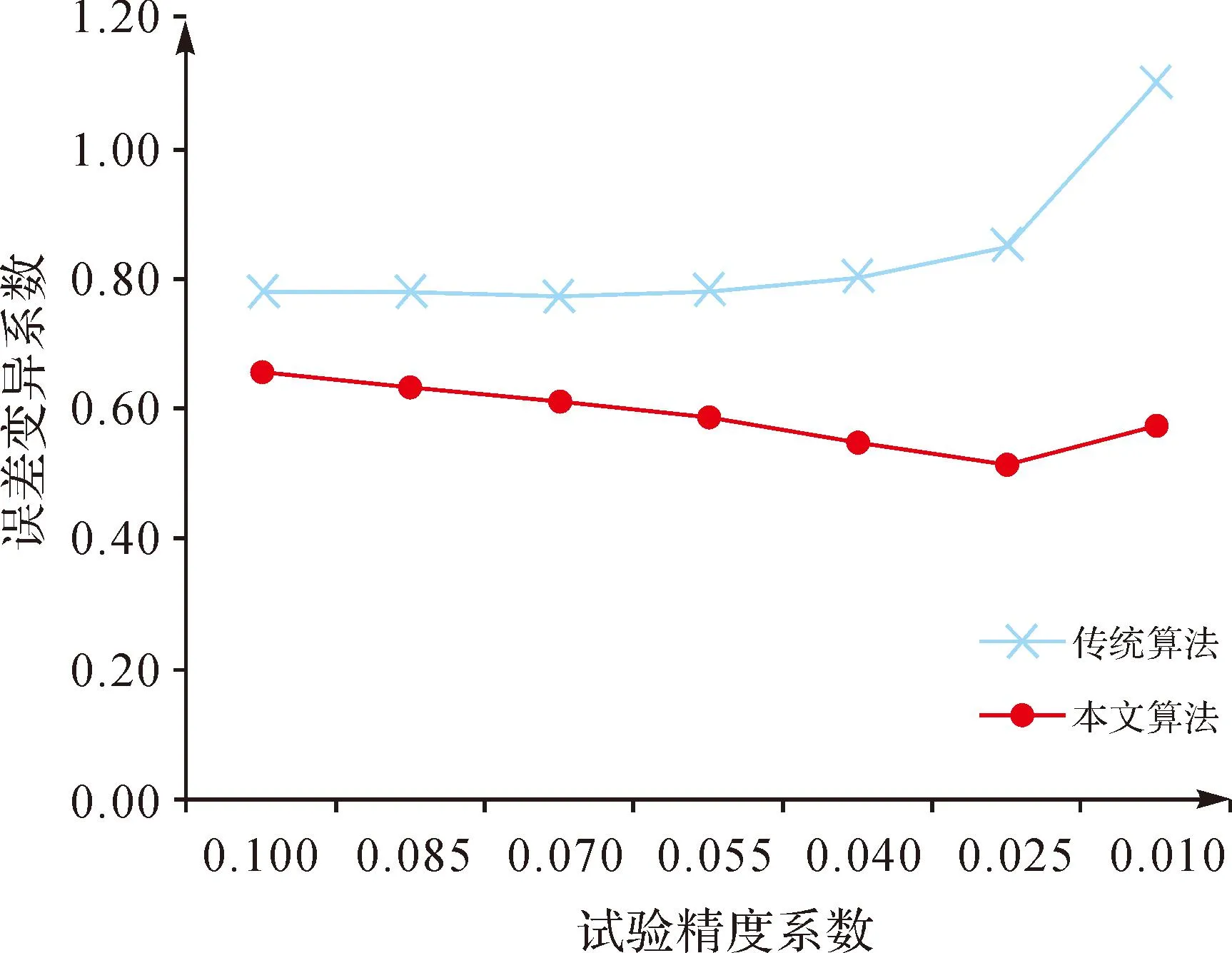
圖8　試驗結果誤差變異系數比較

通過以上3張試驗結果數據比較圖能夠比較直觀地看出，雖然隨著算法精度的提升，兩種算法在壓縮程度上都有所減弱，但是本文算法與傳統的四叉樹算法相比，其在壓縮程度上的表現是具有穩定性和明顯優勢的。由于無限高精度的壓縮是無意義的，因此，在有意義的壓縮精度范圍內，本文算法在壓縮程度上是明顯優于傳統的四叉樹算法的。

通過圖7可以看出，雖然本文算法在誤差均值上比傳統四叉樹算法略有不足，但是，在算法精度達到某一個程度之后，這種差異是明顯減弱的，而由于兩種算法本身在誤差方面的控制就相對比較出色，因此，在一定算法精度內，這種誤差均值上的差異是可以忽略的。而且從圖8中也可以看出，傳統四叉樹算法在誤差分布的穩定性上有明顯的不足，而這種誤差分布穩定性方面的不足會使相同精度下的數據信息丟失更多。與之相比，本文算法在誤差分布上較之傳統四叉樹算法是相對穩定的。因而隨著算法精度的提高，誤差均值的差異逐漸減小，本文算法在誤差分布穩定性上的優勢會使原始數據信息量獲得更大程度的保留。因此，從以上圖表的分析中可以看出，從整體上來說，本文算法較之傳統的四叉樹壓縮算法無論在壓縮程度還是壓縮精度上的表現都是具有較為明顯優勢的。

四、結束語

針對以往基于四叉樹原理的數據壓縮研究中存在的過度分割問題和多波段數據處理問題，本文首先引入“屬性空間”這一概念，將多波段與單一波段數據進行統一化表達，而后針對四叉樹算法的過程特點，在算法迭代返回前設計區域合并方案以彌補過度分割的問題。通過試驗驗證，對于多波段遙感影像數據的壓縮去冗余過程，本文算法較之傳統四叉樹算法在壓縮程度上有50%以上的提升，在誤差控制上都有較為顯著的優勢。同時，由于本文算法可以對任意數量波段進行壓縮合并處理，使其應用范圍突破了以往的數據壓縮存儲局限，因而能夠在基于遙感影像的相關分析處理中達到去除冗余信息、精簡數據的目的。

致謝：感謝武漢大學資源與環境科學學院劉殿鋒老師在論文撰寫過程中給予的大力支持與幫助。

參考文獻：

[1]趙英時.遙感應用分析原理與方法[M].北京：科學出版社，2003.

[2]賈坤,李強子,田亦陳,等. 遙感影像分類方法研究進展[J].光譜學與光譜分析，2011,31(10):2618-2623.

[3]謝順平,馮學智,王結臣,等.一種基于優勢屬性存儲的四叉樹結構及其構建算法[J].武漢大學學報(信息科學版),2009,34(6):663-666.

[4]倪林.基于自適應四叉樹分割的遙感圖像壓縮算法[J].遙感學報,2002,6(5):343-351.

[5]范東光. 圖像的自適應分解算法及應用研究[D].杭州：杭州電子科技大學，2013.

[6]周四龍,粱棟,王慧,等.基于四叉樹與圖割的遙感圖像分割方法[J].計算機工程,2010,36(8):224-226.

[7]ADAM S, PIER LUIGI D. Quadtree Structured Image Approximation for Denoising and Interpolation[J]. IEEE Transactions on Image Processing, 2014, 23(3): 1226-1239.

[8]CHEN H H, DING J J, SHEU H T. Image Retrieval Based on Quadtree Classified Vector Quantization[J]. Multimedia Tools and Applications, 2014, 72(2): 1961-1984.

中圖分類號：P237

文獻標識碼：B

文章編號：0494-0911(2016)02-0032-06

通信作者：丁名時

作者簡介：劉耀林(1960—)，男，教授，主要從事地理數據挖掘與空間分析等方面的研究。E-mail：yaolin610@163.com

收稿日期：2014-12-30

引文格式： 劉耀林，丁名時. 基于四叉樹原理的多波段遙感影像區域合并算法[J].測繪通報，2016(2)：32-37.DOI:10.13474/j.cnki.11-2246.2016.0043.