低軌衛(wèi)星星載GPS數(shù)據(jù)偽距粗差及相位周跳探測(cè)與分析
龔學(xué)文,王甫紅
(武漢大學(xué)測(cè)繪學(xué)院,湖北 武漢 430079)
?
低軌衛(wèi)星星載GPS數(shù)據(jù)偽距粗差及相位周跳探測(cè)與分析
龔學(xué)文,王甫紅
(武漢大學(xué)測(cè)繪學(xué)院,湖北 武漢 430079)
Pseudo-range Outlier and Phase Cycle-slip’s Detection and Analysis of Spaceborne-GPS Data of LEO Satellites
GONG Xuewen,WANG Fuhong
摘要:研究了星載GPS觀測(cè)數(shù)據(jù)中偽距粗差與相位周跳的探測(cè)方法,重點(diǎn)闡述了粗差與周跳探測(cè)有效性檢驗(yàn)的方法。采用自主編制的軟件對(duì)國(guó)內(nèi)外9顆低軌衛(wèi)星(包括我國(guó)的HY2-A與ZY3-A衛(wèi)星)的星載GPS觀測(cè)數(shù)據(jù)的粗差與周跳進(jìn)行了處理與分析。
關(guān)鍵詞:星載GPS數(shù)據(jù);偽距粗差;相位周跳;有效性檢驗(yàn)
隨著GPS接收機(jī)硬件技術(shù)的發(fā)展,將接收機(jī)置于低軌衛(wèi)星平臺(tái)上,可以獲取連續(xù)而密集的GPS觀測(cè)數(shù)據(jù);采用相應(yīng)的數(shù)據(jù)處理技術(shù)進(jìn)行處理,可以用于精確地計(jì)算低軌衛(wèi)星的軌道[1-2]。近些年來(lái),各種類(lèi)型的星載接收機(jī)廣泛搭載在各式不同的低軌衛(wèi)星平臺(tái)上[3-11],星載GPS測(cè)量也成為低軌衛(wèi)星軌道確定的主流技術(shù)之一。進(jìn)行星載GPS實(shí)時(shí)定軌或事后精密定軌,準(zhǔn)確探測(cè)GPS數(shù)據(jù)中的偽距粗差與相位周跳,不但十分必要且重要。與地面載體的GPS測(cè)量不同,低軌衛(wèi)星以每秒數(shù)千米的速度在地球電離層中飛行,星載GPS接收機(jī)處于高速飛行的狀態(tài)中,電離層變化異常顯著,觀測(cè)數(shù)據(jù)所受的電離層延遲變化十分劇烈,偽距粗差及相位周跳等信息往往與地面觀測(cè)數(shù)據(jù)不同,傳統(tǒng)的粗差及周跳探測(cè)方法已不能有效地用于數(shù)據(jù)編輯[12]。
國(guó)內(nèi)外學(xué)者的研究主要集中在相位數(shù)據(jù)的周跳探測(cè)方法上。Bae等對(duì)CHAMP衛(wèi)星數(shù)據(jù)的研究表明,傳統(tǒng)方法(如電離層殘差法、TurboEdit方法等)周跳探測(cè)的成功率低于50%[13]。國(guó)內(nèi)相關(guān)學(xué)者相繼提出了用于相位周跳探測(cè)的歷元間相位差分殘差法(VAREC方法)[14]、二次探測(cè)法[15]與累積和法(CUSUM算法)[16]等,相比于傳統(tǒng)方法,這些方法探測(cè)周跳的效率都有所提高,但對(duì)于方法的有效性,并未提出科學(xué)的檢驗(yàn)體系,同時(shí)也缺乏基于不同衛(wèi)星實(shí)測(cè)數(shù)據(jù)的廣泛驗(yàn)證;此外,對(duì)于偽距粗差的探測(cè),相關(guān)研究往往關(guān)注較少。
本文研究適合于星載GPS數(shù)據(jù)的偽距粗差及相位周跳探測(cè)方法,并重點(diǎn)分析其探測(cè)的有效性檢驗(yàn)方法。基于實(shí)測(cè)數(shù)據(jù),對(duì)國(guó)內(nèi)外常見(jiàn)的處于不同軌道高度的9顆低軌衛(wèi)星的星載GPS觀測(cè)數(shù)據(jù)的粗差與周跳情況進(jìn)行了詳細(xì)的比較分析,從而對(duì)探測(cè)方法進(jìn)行驗(yàn)證。
一、粗差與周跳探測(cè)方法
1. 粗差(周跳)探測(cè)方法
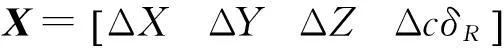
(1)
式中,P為無(wú)電離層偽距組合(一般取P1碼與P2偽距組合);εP為偽距觀測(cè)噪聲(含多路徑效應(yīng));L*為相鄰歷元無(wú)電離層相位組合的差分觀測(cè)值;εL*為其觀測(cè)噪聲(含多路徑效應(yīng))。無(wú)論是探測(cè)粗差或周跳,利用最小二乘原理估計(jì)X,線性化后的方程都可以表示為
(2)
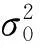
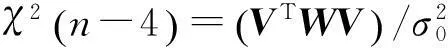
根據(jù)χ2分布假設(shè)檢驗(yàn)結(jié)果,如果判斷該歷元存在粗差,則必須確定哪顆或哪幾顆衛(wèi)星存在粗差。如何從解算殘差V中對(duì)粗差觀測(cè)值進(jìn)行定位,文獻(xiàn)[14]給出了處理步驟:
1) 列出觀測(cè)方程,線性化并進(jìn)行迭代計(jì)算待估量。
2) 對(duì)計(jì)算結(jié)果進(jìn)行χ2分布檢驗(yàn),若檢驗(yàn)接受原假設(shè),表明不含粗差,計(jì)算結(jié)束。

4) 首先認(rèn)為只含有一個(gè)粗差,則先把w1的衛(wèi)星標(biāo)記為剔除,返回到步驟1)和步驟2)重新計(jì)算。若仍不接受原假設(shè),表明該衛(wèi)星數(shù)據(jù)不含粗差或多于1顆衛(wèi)星數(shù)據(jù)含粗差。取消w1的衛(wèi)星剔除標(biāo)記,對(duì)w2的衛(wèi)星作剔除標(biāo)記,重新計(jì)算,直至找出含粗差的衛(wèi)星。
5) 如果進(jìn)行一個(gè)粗差定位時(shí),遍歷所有衛(wèi)星后,依然無(wú)法接受原假設(shè),則認(rèn)為衛(wèi)星數(shù)據(jù)中含有兩個(gè)甚至多個(gè)粗差,一次將兩顆甚至多顆衛(wèi)星標(biāo)記剔除,重新計(jì)算,直至χ2分布檢驗(yàn)接受原假設(shè)結(jié)果。
2. 有效性檢驗(yàn)方法

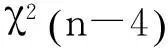
(3)
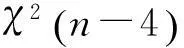
根據(jù)上述分析,為保證粗差(周跳)探測(cè)的有效性及實(shí)際意義,筆者對(duì)σ2的取值設(shè)置遵循以下兩個(gè)基本原則:
1) 一致性原則。本文會(huì)比較不同衛(wèi)星的星載GPS數(shù)據(jù)質(zhì)量情況,因此對(duì)不同的低軌衛(wèi)星的星載GPS數(shù)據(jù)進(jìn)行粗差探測(cè)時(shí),σ2的取值都保持一致,這樣就能夠客觀地比較分析不同衛(wèi)星星載GPS數(shù)據(jù)同一量級(jí)粗差出現(xiàn)的比例情況。
2) 合理性原則。在設(shè)置σ2時(shí),首先應(yīng)該根據(jù)觀測(cè)值的實(shí)際噪聲及誤差情況,控制σ2的合理取值范圍,防止σ2過(guò)大;然后,在合理取值范圍內(nèi),調(diào)整σ2的大小,比較對(duì)應(yīng)的探測(cè)有效率DR,選擇合適的取值。
二、星載GPS實(shí)測(cè)數(shù)據(jù)處理

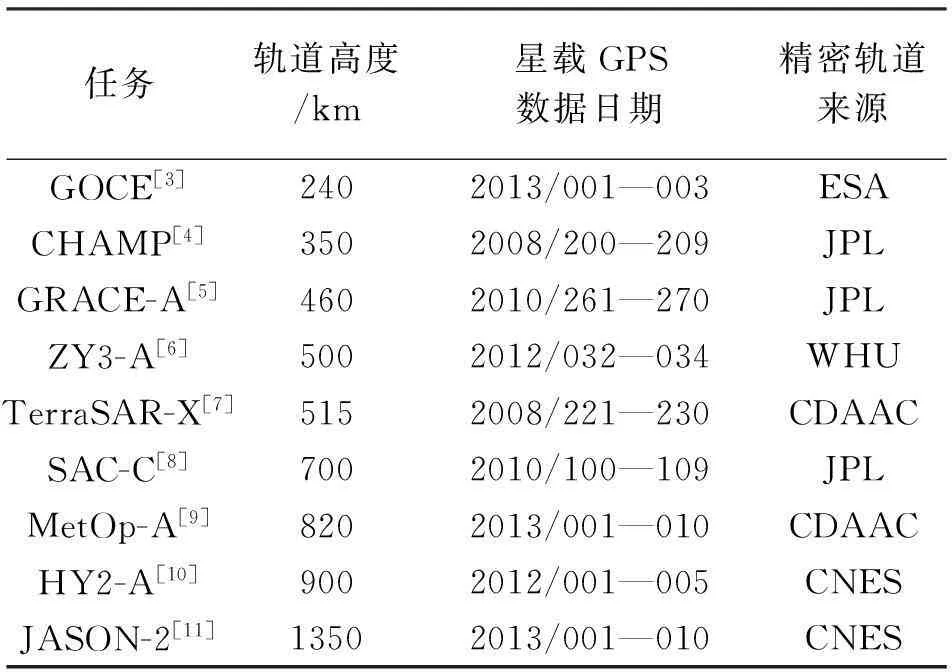
表1 低軌衛(wèi)星及相關(guān)數(shù)據(jù)的主要信息
探測(cè)偽距粗差時(shí),σ2的設(shè)置主要考慮偽距觀測(cè)值多路徑效應(yīng)及噪聲的大小,本文設(shè)置σ2=25.0 m2,即相當(dāng)于探測(cè)大小在3σ=15.0 m以上的粗差。探測(cè)相位周跳時(shí),首先采用TurboEdit方法將一些較大周跳探測(cè)出來(lái),然后采用VAREC方法進(jìn)行探測(cè)。相位觀測(cè)值的多路徑效應(yīng)與噪聲較小(mm級(jí),優(yōu)于1 cm);與GPS真實(shí)的位置及鐘差相比,IGS事后最終星歷與鐘差依然存在一定的誤差(軌道精度為2.5 cm,鐘差精度為75 ps,約為2.25 cm)[18],σ2的設(shè)置綜合考慮相位觀測(cè)值本身的誤差、GPS精密星歷與鐘差的精度及前后歷元差分時(shí)對(duì)誤差的放大,利用近似計(jì)算,取σ2=0.002 5 m2,近似計(jì)算過(guò)程為
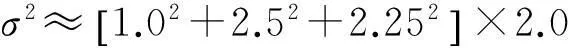
(4)
1. 偽距粗差探測(cè)結(jié)果及分析

從表2可以看出,偽距粗差與衛(wèi)星高度角沒(méi)有必然聯(lián)系,并不是高度角越低,粗差比例就越高,特別說(shuō)明的是,MetOp-A衛(wèi)星的星載接收機(jī)事先剔除了高度角在[0,10°)范圍內(nèi)的觀測(cè)數(shù)據(jù)。GOCE衛(wèi)星偽距觀測(cè)值的粗差比例最低,粗差觀測(cè)值僅有7個(gè);SAC-C衛(wèi)星偽距觀測(cè)值的粗差比例最高,15.512%的歷元存在粗差。
關(guān)于粗差探測(cè)的有效性,所有衛(wèi)星的探測(cè)有效率都在94%以上,部分衛(wèi)星粗差探測(cè)有效率達(dá)到100%。以我國(guó)的HY2-A衛(wèi)星為例,分析粗差探測(cè)有效性驗(yàn)證情況。HY2-A衛(wèi)星的偽距觀測(cè)值共有322 234個(gè),而粗差觀測(cè)值僅有210個(gè)。圖1給出了偽距觀測(cè)值在剔除粗差前后定位誤差的比較,可以看出,如果不剔除粗差,定位誤差高達(dá)千米級(jí),剔除粗差后,定位誤差明顯較小,減小到40 m以下,粗差探測(cè)檢驗(yàn)的有效率達(dá)到100%。
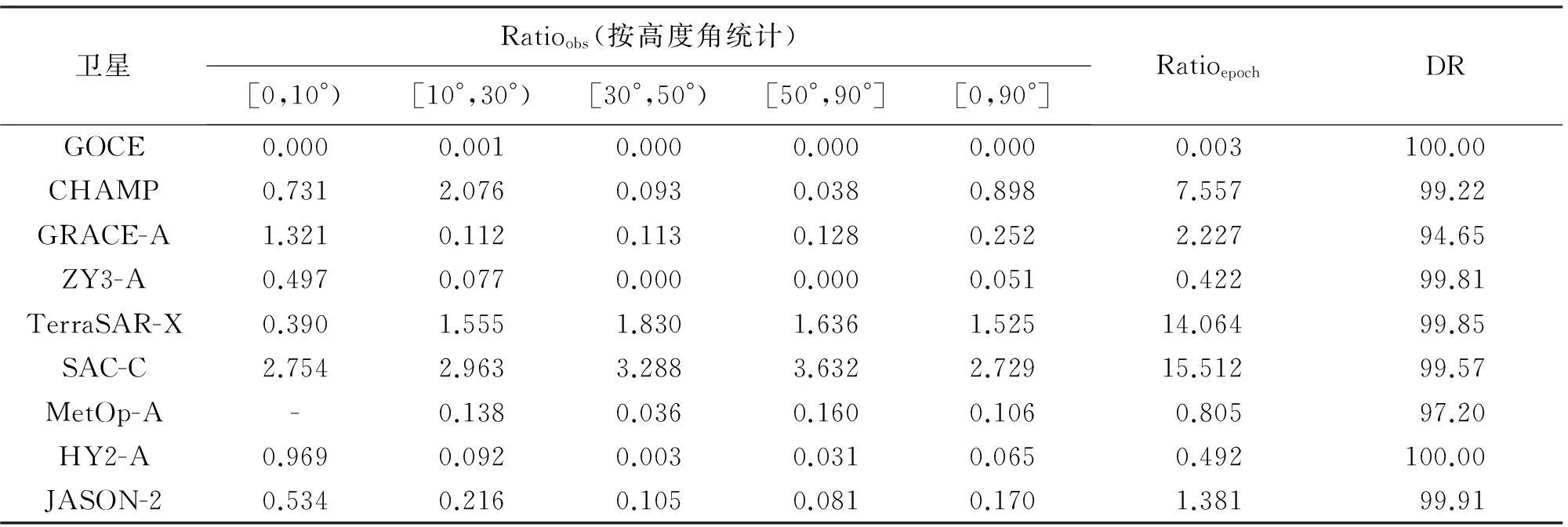
表2 偽距粗差探測(cè)結(jié)果的3個(gè)指標(biāo)參數(shù) (%)
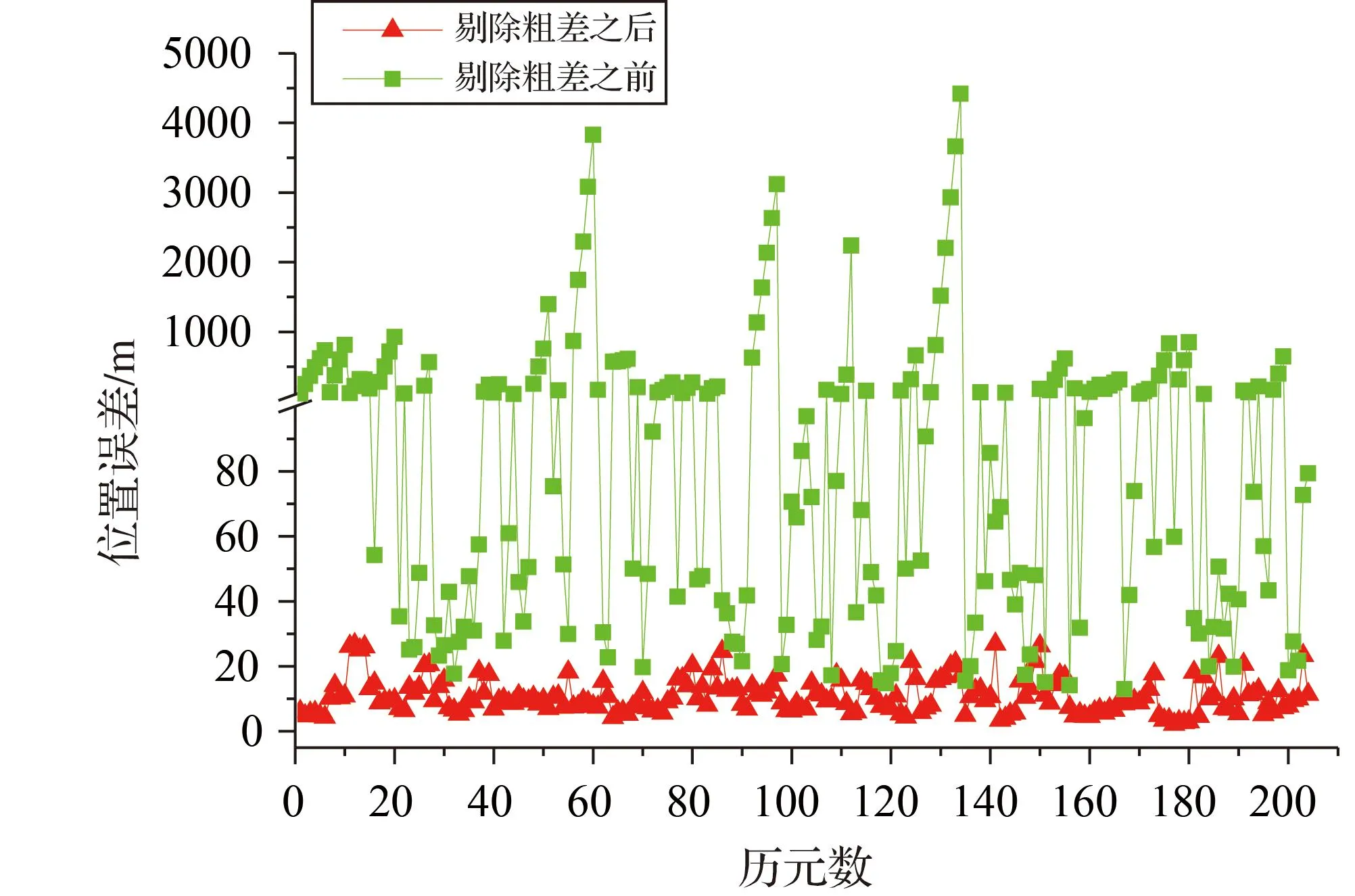
圖1 HY2-A衛(wèi)星偽距粗差探測(cè)有效性檢驗(yàn)
2. 相位周跳探測(cè)結(jié)果及分析


表3 相位周跳探測(cè)的3個(gè)指標(biāo)參數(shù) (%)
從表3可以看出,高度角越低,相位周跳比例就越高,且絕大部分的相位周跳發(fā)生在衛(wèi)星高度角為[0°,10°)與[10°,30°)的范圍內(nèi)。TerraSAR-X與SAC-C衛(wèi)星相位觀測(cè)值的周跳比例最高,發(fā)生周跳的歷元分別達(dá)49.228%與42.206%;GOCE與MetOp-A衛(wèi)星相位觀測(cè)值的周跳比例最低,發(fā)生周跳的歷元分別只有0.035%與0.498%;我國(guó)的HY2-A與ZY3-A衛(wèi)星相位觀測(cè)值的周跳比例較低,分別有10.879%與4.484%的歷元存在周跳。

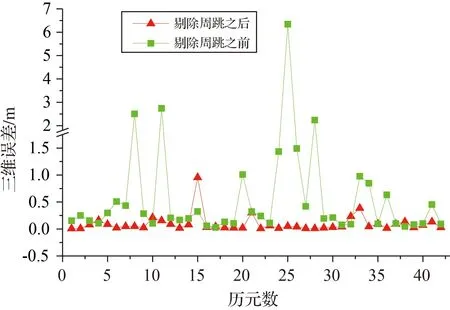
圖2 周跳探測(cè)有效性檢驗(yàn)(GOCE)
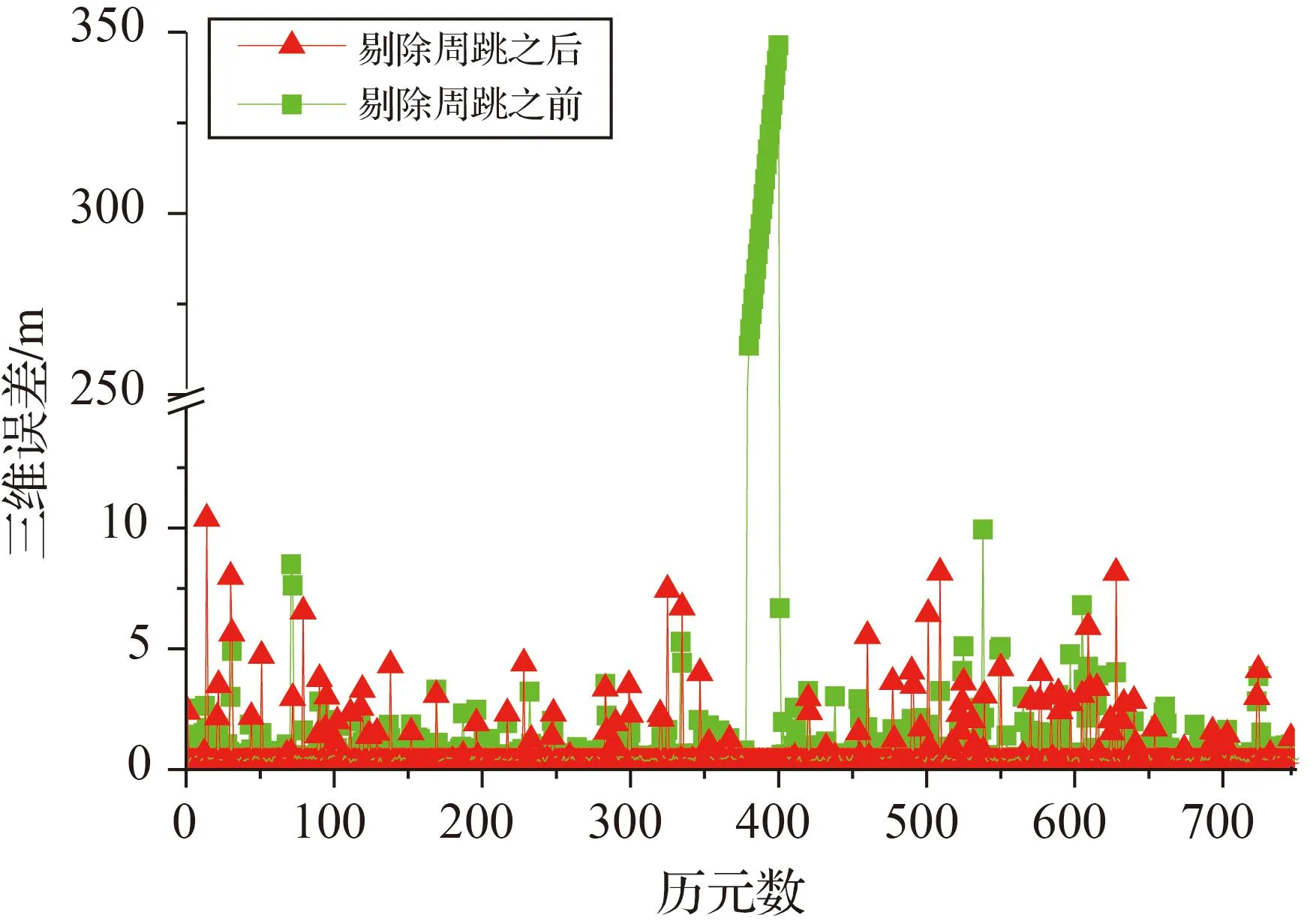
圖3 周跳探測(cè)有效性檢驗(yàn)(MetOp-A)

圖4 周跳探測(cè)有效性檢驗(yàn)(HY2-A)
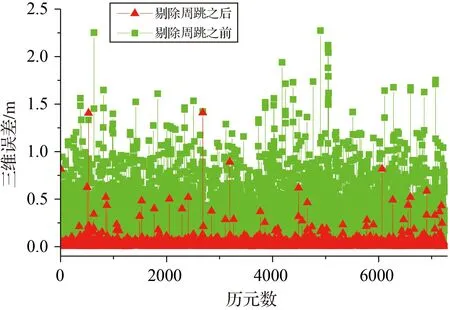
圖5 周跳探測(cè)有效性檢驗(yàn)(ZY3-A)
三、結(jié)束語(yǔ)
本文采用由傳統(tǒng)的TurboEdit方法與VAREC方法相結(jié)合來(lái)探測(cè)相位周跳,基于VAREC方法的基本思路,根據(jù)動(dòng)態(tài)單點(diǎn)定位的殘差來(lái)探測(cè)偽距粗差。對(duì)國(guó)內(nèi)外常見(jiàn)的9顆低軌衛(wèi)星的星載GPS數(shù)據(jù)粗差與周跳情況進(jìn)行了詳細(xì)分析,結(jié)果發(fā)現(xiàn):偽距粗差的分布與衛(wèi)星高度角沒(méi)有必然聯(lián)系;相位周跳的分布與衛(wèi)星高度角有關(guān),高度角越低,周跳發(fā)生的比例越高,絕大部分的周跳發(fā)生在高度角為[0°,10°)與[10°,30°)的范圍內(nèi);此外,絕大部分衛(wèi)星偽距粗差與周跳探測(cè)有效率達(dá)95%以上,個(gè)別衛(wèi)星有效率低于90%,但仍在80%以上。本文充分研究了星載GPS數(shù)據(jù)中偽距粗差與相位周跳的情況,可為星載GPS實(shí)時(shí)或事后定軌計(jì)算提供重要參考。
參考文獻(xiàn):
[1]MONTENBRUCK O, MARKGRAF M, LEUNG S, et al. A GPS Receiver for Space Applications[C]∥Proceedings of ION GPS 2001. Salt Lake City, USA:[s.n.],2001.
[2]SAITO H, HAMADA Y, SHINKAI K, et al. Tiny GPS Receiver for Space Application[J]. Electronics and Communications in Japan (Part I: Communications), 2006, 89(11): 56-67.
[3]BOCK H, JAGGI A, MEYER U, et al. GPS-derived Orbits for the GOCE Satellite[J]. Journal of Geodesy, 2011, 85(11): 807-818.
[4]SVEHLA D, ROTHACHER M. Kinematic and Reduced-dynamic Precise Orbit Determination of CHAMP Satellite over One Year Using Zero-differences[C]∥EGS-AGU-EGU Joint Assembly. Nice, France:[s.n.], 2003.
[5]KANGE Z, TAPLEY B, BETTADPUR S, et al. Precise Orbit Determination for the GRACE Mission Using Only GPS Data[J]. Journal of Geodesy, 2006, 80(6): 322-331.
[6]趙春梅, 唐新明. 基于星載GPS的資源三號(hào)衛(wèi)星精密定軌[J]. 宇航學(xué)報(bào), 2013, 34(9): 1202-1206.
[7]WERMUTH M, HAUSCHILD A, MONTENBRUCK O, et al. TerraSAR-X Precise Orbit Determination with Real-time GPS Ephemerides[J]. Advances in Space Research, 2012, 50(5): 549-559.
[8]HWANG Y, BYOUNG-SUN L, HAEDONG K, et al. Orbit Determination Performances Using Single and Double-differenced Methods: SAC-C and KOMPSAT-2[J]. Advances in Space Research, 2011, 47(1): 138-148.
[9]MONTENBRUCK O, ANDRES Y, BOCK H, et al. Tracking and Orbit Determination Performance of the GRAS Instrument on MetOp-A[J]. GPS Solutions, 2008, 12(4): 289-299.
[10]郭靖,趙齊樂(lè),李敏,等. 利用星載GPS觀測(cè)數(shù)據(jù)確定海洋2A衛(wèi)星cm級(jí)精密軌道[J]. 武漢大學(xué)學(xué)報(bào)(信息科學(xué)版), 2013, 38(1): 52-55.
[11]CERRI L, BERTHIAS J P, BERTIGER W I, et al. Precision Orbit Determination Standards for the Jason Series of Altimeter Missions[J]. Marine Geodesy, 2010, 33(S1): 379-418.
[12]MONTENBRUCK O, KROES R. In-flight Performance Analysis of the CHAMP BlackJack GPS Receiver[J]. GPS Solutions, 2003, 7(2): 74-86.
[13]BAE T S, KWON J H, GREJNER-BRZEZINSKA D A. Data Screening and Quality Analysis for Kinematic Orbit Determination of CHAMP Satellite[C]∥ION Technical Meeting. San Diego:[s.n.], 2002.
[14]王甫紅, 劉基余. 星載GPS載波相位測(cè)量的周跳探測(cè)方法研究[J]. 武漢大學(xué)學(xué)報(bào)(信息科學(xué)版), 2004, 29(9): 772-774.
[15]賴育網(wǎng), 張寅生, 程洪瑋,等. CUSUM算法的星載雙頻GPS周跳探測(cè)研究[J]. 測(cè)繪科學(xué), 2011, 36(1): 42-44.
[16]陳潤(rùn)靜, 彭碧波, 高凡,等. 星載雙頻GPS二次周跳探測(cè)方法研究[J]. 武漢大學(xué)學(xué)報(bào)(信息科學(xué)版), 2012, 37(6): 697-700.
[17]TIBERIUS C, BORRE K. Are GPS Data Normally Distributed?[M]∥Geodesy Beyond 2000: International Association of Geodesy Symposia. [S.l.]:Springer,2000: 243-248.
[18]李征航, 黃勁松. GPS測(cè)量與數(shù)據(jù)處理[M]. 武漢: 武漢大學(xué)出版社, 2005: 85-91.
中圖分類(lèi)號(hào):P228.4
文獻(xiàn)標(biāo)識(shí)碼:B
文章編號(hào):0494-0911(2016)02-0017-05
作者簡(jiǎn)介:龔學(xué)文(1990—),男,碩士,主要從事衛(wèi)星導(dǎo)航定位與衛(wèi)星軌道確定方法的研究。E-mail: 295941068@qq.com
基金項(xiàng)目:國(guó)家自然科學(xué)基金(41374035)
收稿日期:2014-12-25
引文格式: 龔學(xué)文,王甫紅. 低軌衛(wèi)星星載GPS數(shù)據(jù)偽距粗差及相位周跳探測(cè)與分析[J].測(cè)繪通報(bào),2016(2):17-21.DOI:10.13474/j.cnki.11-2246.2016.0040.

