確定采樣型非線性濾波器的研究現狀與發展趨勢*

劉　煒　楊智勇　叢源材　劉群杰　康宇航

(1.91980部隊裝備處　煙臺　264000)(2.海軍航空工程學院　煙臺　264001)(3.91515部隊67分隊　三亞　572016)

?

確定采樣型非線性濾波器的研究現狀與發展趨勢*

劉煒1楊智勇2叢源材2劉群杰3康宇航2

(1.91980部隊裝備處煙臺264000)(2.海軍航空工程學院煙臺264001)(3.91515部隊67分隊三亞572016)

摘要UKF、CDKF和CKF是近年來在國內外得到廣泛研究和應用的一類非線性濾波器,它們具有一個共同的特點就是在濾波過程中通過一組確定采樣點來計算非線性變換后的一二階矩,因此將其統稱為確定采樣型濾波器。論文首先從確定型采樣濾波器的理論發展與其在導航系統的應用出發,介紹了國內外在該領域最新的研究情況。結合確定采樣型濾波器的特點,對UT變換、插值法則、容積法則三種確定采樣型非線性濾波方法進行了介紹。最后,對確定采樣型濾波器的未來發展、應用前景作了展望。

關鍵詞非線性濾波; 確定型采樣; 協方差; 確定采樣

Research Status and Development of Deterministic Sampling Nonlinear Filters

LIU Wei1YANG Zhiyong2CONG Yuancai2LIU Qunjie2KANG Yuhang2

(1. The Office Equipment, No. 91980 Troops of PLA, Yantai264000) (2. Naval Aeronautical and Astronautical University, Yantai264001)(3. Unit 67, No. 91515 Troops of PLA, Sanya572016)

AbstractUKF, CDKF, and CKF belong to the same kind of nonlinear filters which is used widely in recent years. They are called as certainty sample filter because they have one common feature that calculating the first and second moment by a set of certainty sample points in the filtering process. Firstly, this paper introduces the last research status at home and abroad based on the deterministic sampling nonlinear filters’ theory and its application in the navigation. Then three deterministic sampling nonlinear filters’ method which are UT transform, interpolation principle and volume rule are introduced. At last, this paper makes a prospect of deterministic sampling Nonlinear Filters.

Key Wordsnonlinear filtering, deterministic sampling, covariance, deterministic sampling

Class NumberV488.234

1引言

工程實際中遇到的大多數系統,其本質上都是非線性的。但是大部分成熟的理論都是針對線性系統的,因此在建立系統模型時,通常會通過一些假設條件(例如對誤差做小量假設)來忽略系統的非線性因素,從而建立線性系統模型。然而,當假設條件不滿足時,線性化模型就會帶來很大的誤差,此時就必須采用能反映自身實際特性的非線性系統模型。

非線性濾波主要解決對非線性隨機動態系統狀態的估計問題,例如在導航和目標跟蹤的應用中,要求根據含噪聲的量測量對系統狀態進行在線實時估計。由于這些系統大部分是非線性的,因此采用非線性濾波方法對系統狀態進行實時估計是這一領域的重要研究方向。從廣義上講,最優非線性濾波可以通過遞推貝葉斯估計進行統一描述,其中心思想是根據量測量確定非線性系統狀態向量的后驗概率密度函數。基于貝葉斯方法的濾波器以概率密度分布的形式融合了所有可用的信息,通過后驗概率分布獲得概率統計意義下的最優濾波結果,對于非線性和非高斯問題提供了統一的解決方法[1]。貝葉斯估計的最優解只在特殊情況下才能得到,如針對線性高斯系統的卡爾曼濾波器(Kalman Filter,KF)[2]。但是,在實際應用中,由于非線性模型和非高斯噪聲的存在,使得貝葉斯估計難以實現,通常采用近似的方法得到次優解[3]。

針對非線性系統狀態估計,應用最廣泛的是擴展卡爾曼濾波器(Extended Kalman Filter,EKF)[4]。EKF需要通過一階泰勒級數展開的方法將非線性系統方程進行線性化,因此只適用于弱非線性系統[5]。當系統非線性增強,估計誤差增大甚至發散,因此以UKF(Unscented Kalman Filter)[6～9]為代表的確定采樣近似方法近年來得到廣泛關注,不同于粒子濾波隨機采樣方法,確定采樣型濾波器(Deterministic Sampling Filters,DSFs)通過一組確定采樣點對一二階矩進行近似計算,計算量與EKF相近,估計精度較EKF有較大提升。

另一類研究較多的非線性濾波器是粒子濾波器(Partical Filter,PF)[10],粒子濾波器基于Monte Carlo模擬方法,通過統計采樣對經驗條件分布進行調整來近似后驗概率密度。這種方法尚不成熟,還有很多問題需要解決,如建議分布的選取、采樣方法以及計算量大等問題[11]。

在線實時估計對濾波算法的要求是:計算量小、精度高和穩定性好。盡管PF的精度很高,但是由于計算量太大,不適用于在線實時估計。DSFs和EKF相比,計算量相當,DSFs的精度更高。用DSFs取代EKF對非線性系統狀態進行實時估計成為濾波理論研究的一個重要方向,而目前關于DSFs的研究多集中在該方法在不同領域的應用,對該方法本身的精度和穩定性的理論研究卻較少。

確定采樣型濾波器在濾波過程中,采樣點的選取對濾波器的精度和穩定性起著決定性作用,對選取的采樣點進行優化可以提高濾波效果。

2國內外研究現狀

確定采樣型濾波器的出現可以追溯到1994年,牛津大學的Julier和Uhlmann[6]從“近似非線性函數的概率密度分布比近似非線性函數本身更容易”這一思路出發,提出通過一組按確定規則選取的采樣點對一二階矩進行擬合來完成一二階矩的傳遞。這種被稱為UT變換(Unscented Transform)的一二矩計算方法不需要計算雅克比矩陣,而且比一階泰勒級數展開的線性化具有更高的精度。之后,Julier等對該方法的采樣策略進一步完善,提出了多種不同的采樣策略,包括對稱采樣,單形采樣[12],3階矩偏度采樣和高斯分布4階矩對稱采樣等[13]。隨著這一系列的研究,確定采樣型濾波器也應運而生。目前學術界主要研究的確定采樣型濾波器主要有三種,分別為UKF(Unscented Kalman Filter)、CKF(Cubature Kalman Filter)以及CDKF。

2.1UKF

將UT變換與KF相結合就得到了UKF(Unscented Kalman Filter)。目前,UKF已經在諸多領域得到應用。

UKF的成功應用,吸引了更多學者對UKF算法的理論研究。首先是Julier發現在應用單形采樣和對稱采樣時,UKF在濾波過程中出現非局部效應和協方差陣非正定問題,提出了對采樣點進行比例修正的方法[18],該方法提供了三個自由參數來調整采樣點到采樣中心的距離和權值,但并沒有給出參數調整具體方法。

由于選取采樣點需要使用協方差矩陣的平方根矩陣,當協方差矩陣出現非正定時,無法獲得采樣點。為了解決這一問題,Merwe[14]在2001年提出在濾波過程中采用協方差矩陣的平方根矩陣代替協方差矩陣,這種方法避免了濾波過程中對協方差矩陣的分解,但是導致協方差矩陣非正定的因素并沒有消除。協方差矩陣出現非正定,主要是因為采樣點權值中存在負值,因此Lefebvre[15]在2002年提出增加一個權值為1的中心采樣點來增大協方差矩陣從而保證協方差矩陣正定,但是這種方法可能會降低濾波器精度。Xiong[16]在2006年提出通過人為增大系統噪聲矩陣增加濾波器的穩定性,這種方法其實就是保證了協方差矩陣的正定性,與Lefebvre的方法是等價的,同樣是以犧牲精度為代價提高穩定性。

2.2基于球面徑向容積法的CKF

在2009年提出了基于球面徑向容積法的CKF(Cubature Kalman Filter)[17]。雖然CKF通過球面徑向容積法則獲取的采樣點可以看作是UKF采樣點的特例,但是其獲得采樣點的方法為實現高精度的采樣點提供了理論基礎。從數值積分的角度,2011年哥倫比亞大學的Jia[18]提出了減少采樣點數目的GHF,隨后2012年在此基礎上提出的SGQF(Sparse-Grid Quadrature Filter)[19]和2013年提出的高階CKF[20],提高了濾波器的精度(事實上,兩種方法所選取的采樣點是相同的)。CKF的提出解決了UKF中出現采樣點權值為負的問題,但同時也帶來了非局部效應,即采樣點離采樣中心的距離會隨著系統維數的增加而增大,從而限制了CKF在高維系統中的應用。針對這一問題,Chang[21]巧妙地構建了一個正交矩陣,通過對CKF的采樣點進行正交變換的方法得到了一組新的采樣點,這組采樣點離采樣中心保持固定的距離,不會隨系統維數的改變而變化,由此消除了非局部效應。

2.3CDKF

與UKF提出的目的一樣,為了避免雅可比矩陣的計算,Schei[22]在1997年提出基于插值法則的非線性濾波方法,將狀態協方差矩陣進行分解后得到的平方根矩陣看作是在狀態向量空間各個方向上的擾動,然后通過積分中值定理得到非線性變換后的協方差矩陣的平方根矩陣,從而完成協方差矩陣的傳遞。這種方法最大的優勢就是避免了雅克比矩陣的求解,雖然在精度上并沒有多大提升,但是提供了一種解決非線性濾波問題的新思路。2000年,N?rgaard等[23]在此基礎上提出了DDF(Divide Difference Filter),采用基于Sterling多項式差值法則的中心差分方法代替Jacobian/Hessian矩陣對非線性函數的泰勒級數展開進行多項式近似;與此同時,Ito提出了基于數值積分近似的CDF(Central Difference Filter)[5]。CDF和DDF的出發點都是對泰勒級數展開式的近似,在本質上是相同的,因此Merwe[24]將其統稱為CDKF,并在其博士論文中證明了CDF與DDF的等價關系[25]。

3確定采樣濾波器主要采樣方法

確定采樣型濾波器在非線性高斯濾波框架下通過對一二階矩近似實現狀態估計,濾波過程如下:

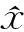
2) 狀態傳遞方程:

χi=f(σi)

(1)

(2)

(3)

3) 量測更新方程:

ξi=h(χi)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

目前得到應用廣泛的UKF、CDKF和CKF,都是采用這一濾波過程,它們的不同之處在于選取不同的采樣點計算一二階矩。下面對它們的采樣方法進行介紹。

3.1UT變換

UKF采用一種被稱為UT變換的方法對一二階矩進行擬合,在1994年牛津大學的Julier和Uhlmann[6]提出該算法的時候并沒有詳細的理論依據和推導過程,只是出于近似概率分布比近似非線性方程更容易的考慮。隨后作者發表了一系列文章對該算法進行完善,在2004年[8]發表的文章中對關于該算法做了完整的總結,建議采用對稱采樣和比例修正采樣。

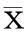
3.2插值法則

CDKF是Ito[26]提出的CDF和N?rgaard[14]提出的DDF的統稱,都是基于多項式函數擬合的方法來計算一二階矩。

1997由Schei[22]首先提出了采用差分公式來代替EKF中的非線性方程求導,雖然只采用了一階近似,精度沒有提高,但是提供了一條濾波器發展的思路。2000年,N?rgaard在Schei的多項式差值近似基礎上,受UKF的啟發,提出了DD1和DD2,即DDF。與此同時,Ito從數值積分近似狀態后驗分布得到了CDF。多項式差值近似和數值積分近似在本質上都是基于多項式函數擬合的思想。

3.3容積法則

對狀態后驗分布的數值積分近似是非線性濾波器發展的一個重要方向,Arasaratnam在2009年提出的CKF[20]就是基于數值積分的近似方法對一二階矩進行計算。CKF采用球面徑向法則,通過2n個采樣點來實現濾波。

4未來的發展趨勢

UKF、CKF和CDKF的采樣點和一二階矩的計算中有很多共同點,它們的核心思想可以統一歸納為[27]:首先根據狀態先驗分布按照一定的規則選取一定數量的采樣點;然后將這些采樣點經非線性變換后按照一定的規則進行組合來逼近經非線性變換后的狀態分布。因此,可以將其統稱為確定采樣型濾波器。它們的不同之處就在于采樣點的選取和組合規則的不同,在處理不同的非線性系統時,會得到不同的結果。通過建立采樣點與數值積分節點之間的對應關系,就可以對這一類濾波器進行精度分析,這是確定采樣型濾波器未來發展的方向之一。

除了精度比較之外,關于確定采樣型濾波器的穩定性的分析也是判斷濾波器適用范圍的重要依據。目前關于這一類濾波器的穩定性分析的結論主要是在泰勒級數展開線性化條件下得到的,北京航空航天大學的Xiong[16]對UKF穩定性進行了分析,給出了濾波器穩定的條件,由于UKF對初始誤差非常敏感,當初始誤差較大時,會出現濾波發散,因此提出在協方差矩陣中增加一個正定的誤差矩陣,可以降低對初始誤差的要求,從而提高UKF的穩定性,但是如果誤差矩陣設定過大會導致精度下降。為了保證濾波器的穩定性,需要增大噪聲協方差矩陣,Lefebvre[15]指出這種做法會導致濾波收斂速度減慢和精度下降。

要對這一類濾波器進行精度和穩定性分析,必須要建立一個統一的結構。從確定采樣型濾波器的推導過程看,濾波器結構可以從不同的角度得出。各種確定采樣型濾波器可以通過遞推貝葉斯估計得到統一的濾波器結構,文獻[5]中,Ito將條件概率密度假設為高斯分布,通過貝葉斯法則建立了高斯濾波器結構,利用對貝葉斯法則的有效數值積分實現了最優的遞推濾波,通過濾波增益和量測信息對均值和協方差的預測值進行修正從而得到狀態估計值。對于濾波過程中用到的均值和協方差可以通過數值積分的近似方法得到,因此在該結構下確定采樣策略與數值積分的結合可以將濾波器精度轉化為數值積分的精度問題。

Lefebvre[15]利用統計線性回歸的方法推導出了統計線性回歸卡爾曼濾波器,并指出UKF和CDKF均屬于這種濾波器。Arasaratnam在文獻[3]中同樣是基于統計線性回歸的濾波器結構,采用數值積分的方法計算一二階矩,得到了QKF。該結構采用的是通過一二階矩將非線性方程線性化的方法從而直接套用KF的濾波公式。這種結構最大的優點就是可以用關于KF穩定性的成熟理論來分析確定采樣型濾波器的穩定性。

目前對于確定采樣型濾波器的改進主要是將傳統的針對KF和EKF的方法與現有濾波方法的結合,如文獻[28]將自適應估計技術和UKF和DDF結合,對濾波過程中的線性化誤差以及系統建模誤差進行補償。當前已有文獻大都集中于確定采樣型濾波的應用研究,理論上還有很多問題有待進一步研究。

5結語

本文主要基于模糊控制理論,對航跡跟蹤系統進行研究和設計。設計了基于模糊控制的飛機傾斜姿態控制器,在此基礎上,以飛機傾斜姿態控制器為內回路,設計了飛機橫側向航跡跟蹤控制器。通過與傳統PID控制器比較表明,模糊控制方案無論在穩定性還是控制精度上都有所提高,體現了模糊控制的優越性。通過仿真驗證,說明本文設計的系統能夠實現對航跡的精確跟蹤,該方案是切實可行的。

參 考 文 獻

[1] Y C Ho, R C K Lee. A bayesian approach to problems in stochastic estimation and control[J]. IEEE Transactions on Automatic Control,1964,AC-9(10):333-339.

[2] Kalman R E, Bucy R S. A new approach to linear filtering and prediction problems[J]. Transactions of the ASME-Journal of Basic Eng by ASME,1960,82D:34-45.

[3] I Arasaratnam, S Haykin, R J Elliott. Discrete-time nonlinear filtering algorithms using Gauss-Hermit quadrature[J]. Proceedings of IEEE,2007,95(5):953-977.

[4] Bucy R S, Renne K D. Digital synthesis of nonlinear filter[J]. Automatica,1971,7(3):287-289.

[5] K Ito, K Xiong. Gaussian filters for nonlinear filtering problems[J]. IEEE Transactions on Automatic Control,2000,45(5):910-927.

[6] S Julier, J Uhlmann. A general method for approximating nonlinear transformations of probability distributions[R]. Robotics Research Group, Department of Engineering Science, University of Oxford,1994:78-84.

[7] S Julier, J Uhlmann, H F Durrant-Whyte. A new approach for filtering nonlinear system[C]//Proceedings of the American Control Conference, Washington, DC.,1995:1628-1632.

[8] S Julier, J Uhlmann. Unscented filtering and nonlinear estimation[J]. Proceedings of the IEEE,2004,92(3):401-422.

[9] S Julier, J Uhlmann, H F Durrant-Whyte. A new method for the nonlinear transformation of means and covariances in filters and estimators[J]. IEEE Transactions on Automatic Control,2000,45(3):477-482.

[10] Gordon, N J, Salmond, D J, Smith, A F M. Novel approach to nonlinear/nonaussian bayesian state estimation[J]. IEE Proceedings,1993,140(2):107-113.

[11] 胡士強,敬忠良.粒子濾波算法綜述[J].控制與決策,2005,20(4):361-371.

[12] S Julier, J Uhlmann. Reduced sigma point filters for the propagation of means and covariances through nonlinear transformations[C]//Proceedings of American Control Conference. Jefferson City,2002:887-892.

[13] S Julier. The scaled unscented transformation[C]//Proceedings of American Control Conference. Anchorage: Institute of Electrical and Electronics Engineers Inc,2002:4555-4559.

[14] Van der Merwe, Rudolf, Wan, Eric. The Square-Root Unscented Kalman Filter for state and parameter-estimation[C]//Proceedings of International Conference on Acoustics, Speech, and Signal Processing(ICASSP), Salt Lake City, Utah,2001,5.

[15] T Lefebvre, H Bruyninckx, et al. Comment on “A New Method for Nonlinear Transformation of Means and Covariances in Filters and Estimations”[J]. IEEE Transations on Automatic Control,2002,47(8):1406-1408.

[16] Xiong K, Zhang H Y, Chan C W. Performance evaluation of UKF-based nonlinear filtering[J]. Automatica,2006,42(2):261-270.

[17] I Arasaratnam, S Haykin. Cubature Kalman Filters[J]. IEEE Transactions on Automatic Control,2009,54(6):1254-1269.

[18] B. Jia, M. Xin, Y. Cheng. Sparse Gauss-Hermite quadrature filter with application to spacecraft attitude estimation[J]. Journal of Guidance, Control and Dynamics,2011,34(2):367-379.

[19] B. Jia, M. Xin, Y. Cheng. Sparse-grid quadrature nonlinear filtering[J]. Automatica,2012,48(2):327-341.

[20] Jia B, Xin M, Cheng Y. High-degree Cubature Kalman Filter[J]. Automatica,2013,49(2):510-518

[21] Lubin Chang, Baiqing Hu, An Li, et al. Transformed Unscented Kalman Filter[J]. IEEE Transactions on Automatic Control,2013,58(1):252-257.

[22] T S Schei. A finite-difference method for linearization in nonlinear estimation algorithms[J]. Automatica,1997,33(11):2053-2058.

[23] M N?rgaard, N K Poulsen, O Ravn. New developments in state estimations for nonlinear systems[J]. Automatica,2000,36(11):1627-1638.

[24] Merwe R V, Wan E A. Sigma-point Kalman filters for integrated navigation[C]//Proceedings of the 60th Annual Meeting of the Institute of Navigation. Dayton: Institute of Navigation,2004:641-654.

[25] R Merwe. Sigma-point Kalman filters for probabilistic inference in dynamic state-space models[D]. Oregon: Electrical and Computer Eng. Dept., Oregon Health & Science University,2004:464-468.

[26] Ito K, Xiong K. Gaussian filters for nonlinear filtering problems[J]. IEEE Transactions on Automatic Control,2000,45(5):910-927.

[27] Simandl M, Dunrik J. Derivative-free estimation methods: new results and performance analysis[J]. Automatica,2009,45(7):1749-1757.

[28] Deok-Jin Lee, Kyle T Alfriend. Adaptive sigma point filtering for state and parameter estimation[C]//AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Providence, Rhode Island, AIAA 2004-5101.

中圖分類號V488.234

DOI:10.3969/j.issn.1672-9730.2016.01.041

作者簡介:劉煒,男,工程師,研究方向:自動控制。楊智勇,男,博士,副教授,研究方向:模式識別。叢源材,男,博士,助理工程師,研究方向:導航制導與控制。劉群杰,男,助理工程師,研究方向:測控技術與儀器。康宇航,男,博士,研究方向:導航制導與控制。

*收稿日期:2015年7月10日,修回日期:2015年8月26日