非平穩地震激勵下隔震曲線梁橋振動控制研究①

(1.蘭州理工大學 西部土木工程防災減災教育部工程研究中心，甘肅 蘭州 730050；

2.蘭州理工大學 防震減災研究所，甘肅 蘭州 730050)

?

非平穩地震激勵下隔震曲線梁橋振動控制研究①

(1.蘭州理工大學 西部土木工程防災減災教育部工程研究中心，甘肅 蘭州 730050；

2.蘭州理工大學 防震減災研究所，甘肅 蘭州 730050)

摘要：曲線梁橋由于其平面不規則性導致結構在地震激勵下產生彎扭耦合效應，使得隔震曲線梁橋的地震響應更加復雜。目前常用的控制方法是將隔震技術與附加減震裝置相結合對曲線梁橋進行控制。本文將地震動考慮為一均勻調制非平穩隨機過程，針對隔震曲線梁橋長周期、低頻率的特點，選取Clough-Pension平穩地震動功率譜模型作為隨機地震動輸入模型，對無控(NON-C)、經典線性最優控制(COC)以及序列最優控制算法(SOC)三種狀態下的曲線橋梁進行隨機響應分析。通過建立曲線梁橋在隨機地震動作用下的運動方程，求出減震控制結構的位移譜密度、加速度譜密度響應及時變方差。分析結果表明：序列最優控制算法(SOC)在使隔震層位移得到減小的同時，可以更有效地控制上部結構的地震響應，具有更好的控制效果。

關鍵詞：曲線梁橋； 最優序列控制； 虛擬激勵法； 隨機響應

0引言

目前對于曲線梁橋控制動力反應研究較多采用確定性分析方法[1-4]。但是地震動是一個隨機過程，導致地震作用下減震結構的動力反應也必然為隨機過程，因此采用確定性的地震激勵不具有代表性，而采用隨機振動理論能更好地反映響應的統計特性，求解得到的結果也更為合理[5]。

經典最優控制算法計算過程需要求解非線性RICCATI方程，而自由度數量太多的有限元模型會給求解帶來嚴重困難。作者針對經典最優控制算法的缺點，借鑒離散系統最優控制的Bellman最優法則，在每一個時間步長上建立目標函數，推導出更為一般的序列最優控制算法(SOC)，并應用于隔震曲線梁橋的控制分析。

本文根據曲線梁橋受力特點，考慮隔震曲線梁橋上部結構剛度中心與質量中心不一致造成的平扭耦合的地震效應，對隔震曲線梁橋建立雙質點六自由度控制分析模型。選擇Clough-Pension 功率譜密度函數模型，并采用虛擬激勵法求解動力方程，通過MATLAB編程對無控(NON-C)、經典線性最優控制(COC)以及序列最優控制算法(SOC)三種狀態下曲線橋梁的隨機地震響應進行分析。

1隔震曲線梁橋模型的建立

1.1模型假設

首先將隔震曲線梁橋橋墩和上部結構簡化為兩個模型系統，各具有兩個水平x、y自由度和一個圍繞質量中心軸扭轉θ自由度，堆積質量為m1、m2。橋墩與上部結構為兩質點非同軸質量偏心結構的分析模型，上下質點分別表示曲線橋下部結構和上部結構(圖1)[6]。

圖1　曲線梁橋計算模型簡圖Fig.1　Computational model of the curved bridge

1.2運動方程的建立

取曲線橋上部結構的質量中心處為坐標原點，曲線梁橋動力方程可表示為：

(1)

(2)

其中：

(3)

式中：m1、m2分別為下部結構和上部結構的質量;J1、J2分別為下部結構和上部結構的轉動慣量[7]；ri為回轉半徑；Xmi、Ymi分別為下部結構和上部結構質心相對于參考軸的坐標;Kxx、Kyy分別為結構在x、y向的平動剛度，取隔震橋梁結構為剪切型;Kxθ、Kyθ分別為結構x、y向的平扭剛度，并考慮上部結構與下部結構質心與剛心的偏心距及上部結構與下部結構質心之間的偏心距;Kθθ為結構的扭轉剛度矩陣。

(4)

式中：Kx1、Ky1和Kx2、Ky2分別表示下部結構和上部結構的平移剛度；Kxθ12、Kyθ12分別表示僅m2發生x向、y向單位位移時，在m1所需施加的繞z軸的力矩；Kθθ12表示m1不動，僅m2發生單位轉角時，在m1所需施加的繞z軸的力矩;Kxθ11，Kxθ22，Kxθ21，Kyθ11，Kyθ22，Kyθ21，Kθθ11，Kθθ22，Kθθ21表示含義以此類推[8]。

阻尼矩陣[C]采用分區瑞利阻尼模型，阻尼矩陣可分解為

(5)

式中:[Cr]為體現非比例阻尼的余項阻尼矩陣;Cbr=(αb-αs)mb+(βb-βs)kb;[C0]代表經典瑞利阻尼矩陣;αs、βs、αb、βb分別為下部結構和隔震系統的瑞利阻尼比例系數。

(6)

式中：ξs，ξb分別為下部結構和隔震系統的瑞利阻尼比例系數；ωi、ωj為結構的第i,j階圓頻率[9]。

1.3序列最優控制算法

目前時域內結構最優控制算法大多是對問題做了簡化的，作者推出的序列最優控制算法吸收了幾種常見算法的優點，并對現有算法進行改進，將控制目標函數化解到每個時間步長上，推導出更為一般的最優控制算法，并用狀態轉移的數值方法加以實現[10-12]。

最優控制力模型可根據作者提出的狀態反饋序列最優控制算法，構造雙向地震作用下的二次型控制目標函數為

(7)

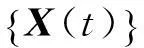
(8)

式中：下標“∑(j-1)”代表直到第(j-1)個步長上(過去時刻)脈沖影響的總和，將式(8)代入式(7)后，構造Lagrange函數，則原約束優化問題轉化為無約束問題。

因為當前時刻的脈沖只影響當前時刻和未來時刻的響應，對過去時刻的響應沒有影響，因此把純粹包含過去時刻脈沖影響的控制目標函數分離開來，引用最優控制理論的泛函極值條件，可得到結構最優控制的一般表達式：

(9)

(10)

式中：tA為當前時刻;式(9)、(10)的定義域為 [tA,tf]。

序列最優控制算法同時包含了每個瞬刻的結構響應和外部地震激勵的影響，因此除了數值方法的固有計算誤差外，從概念上講本文算法是精確解。

2曲線梁橋隨機地震響應求解

2.1隨機地震動模型

均勻調制模型為一個確定性強度包線函數與一個平穩隨機過程的乘積，即f(t)=g(t)X(t)。式中g(t)為確定性強度包線函數;X(t)為平穩隨機過程。g(t) 采用Jennings提出的一個非平穩強度包線函數的形式：

(11)

式中：t1、t2和c分別表示主震段的首、末時間和衰減函數;T為主震的持續時間[13]。

平穩隨機過程X(t)由功率譜唯一確定，本文的研究對象是隔震體系，選用Clough-Penzion建議的表達式，即地震動的單邊功率譜可表示為

(12)

(13)

(14)

式中:S0為譜強度因子；ξs、ωg分別為地基土的阻尼比和卓越頻率;ξc、ωc兩參數的配合可模擬地震動低頻能量的變化[14]。

該模型為雙過濾白噪聲，相當于使白噪聲信號經過兩個單自由度的線性濾波器，能解決Kanai-Yaijmi模型過分強調低頻的缺陷。

2.2虛擬激勵法求解

將式(1)轉化成狀態空間表達式：

(15)

(16)

(17)

3實例計算

3.1工程背景

某立交匝道上一聯圓曲線連續梁橋，跨徑為3×20 m，曲率半徑R為50 m，圓心角θ為69°，主梁采用單箱單室箱梁。為簡化分析，采用獨柱式圓形橋墩，直徑1.5 m，墩高為5 m，橋墩墩底固結，每個墩頂布置圓形鉛芯橡膠支座。結構的阻尼比下部結構ξs為0.05，隔震層的水平阻尼比ξb為0.15，上部結構質心處為整體坐標系原點。

每個橋墩位置處切向和徑向各設置一組理想智能控制器來連接墩臺和主梁，最大阻尼力2 000 kN，如圖2所示。采用狀態反饋序列最優控算法對結構進行控制，設控制器能夠實時提供所需的控制力，且不計時滯和自身動力效應。

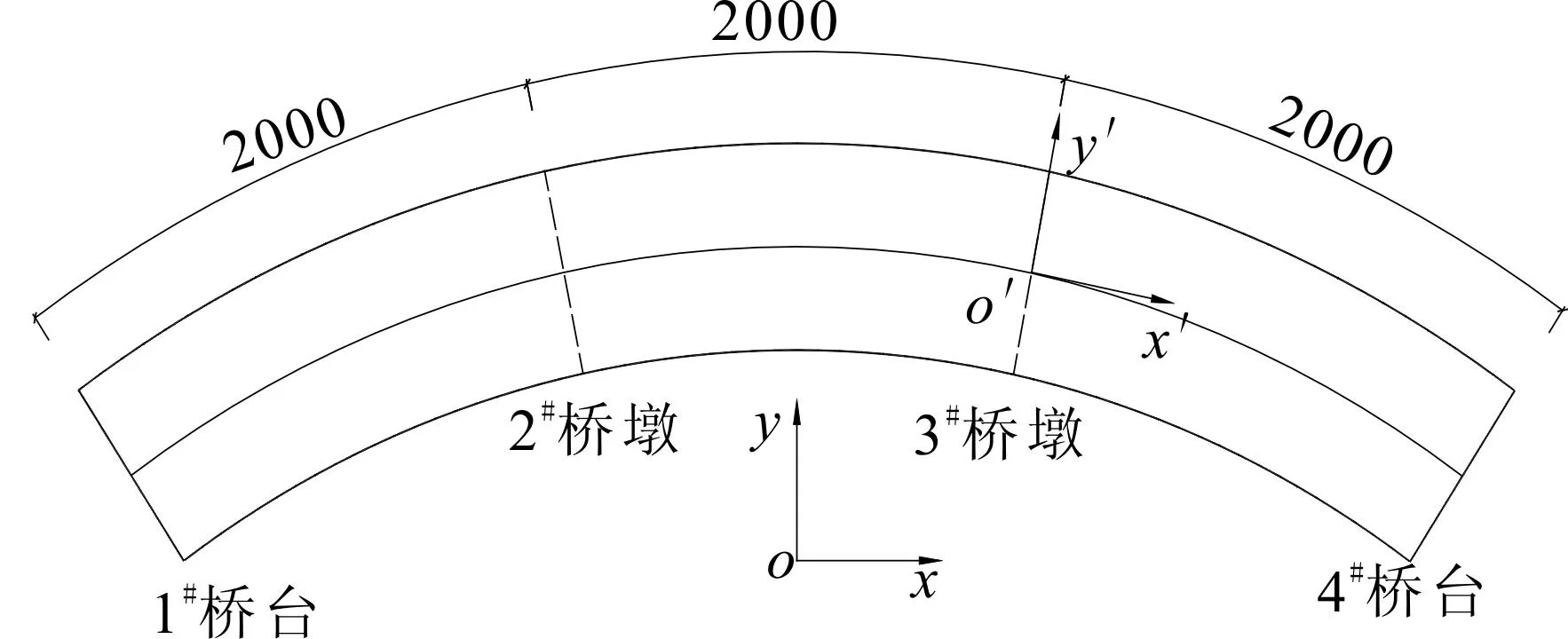
圖2　曲線梁橋平面Fig.2　Plan of the curved bridge

3.2隨機響應分析

取非平穩隨機過程強度包線函數參數t1=2.3，t2=16.2，c=0.98，T=20 s。以設防烈度Ⅷ度為例，按照雙過濾白噪聲模型， 推算“大震”的基巖單邊譜強度分別為S0=2×0.024 92 m2/s-3。場地選用Ⅱ類場地土設計，地震分組按第一分組考慮，低頻過濾器參數ωg=15.7，ξg=0.72，取ξc=ξg，ωc=0.15ωg，得到的輸入地震動加速度的功率譜密度如圖3所示[16-17]。

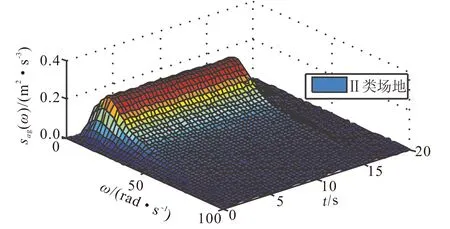
圖3　地震動加速度功率譜Fig.3　Seismic acceleration power spectrum

按照上述平穩過濾白噪聲激勵下的隨機狀態反應分析的過程描述，用MATLAB進行編程分析，分別求出隔震曲線梁橋在無控和有控狀態下的功率譜和均方值。

圖4和圖5分別為曲線梁橋上部結構在無控(NON-C)、經典線性最優控制(COC)以及序列最優控制算法(SOC)三種狀態下位移功率譜密度和加速度功率譜密度的對比圖。

由圖4、圖5可以看出，相同控制能量下，三種狀態下位移功率譜密度和加速度功率譜密度峰值均位于曲線梁橋一階自振頻率附近。與無控狀態相比，兩種控制算法的位移功率譜密度和加速度功率譜密度

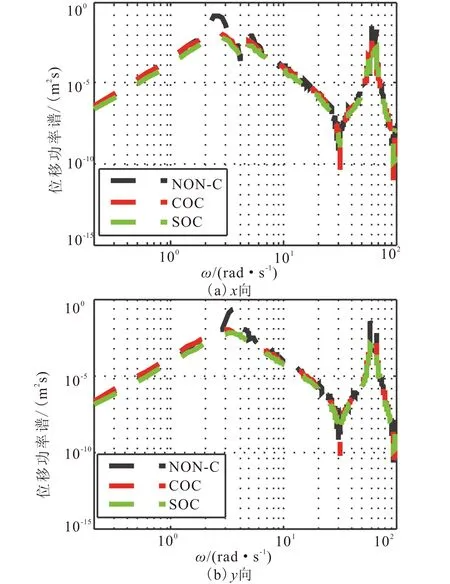
圖4　上部結構位移功率譜密度Fig.4　The displacement power spectral density of superstructure

圖5　上部結構加速度功率譜密度Fig.5　The acceleration power spectral density of　　　 superstructure

峰值都大大降低。序列最優控制算法(SOC)降低x向位移和加速度功率譜峰值的效果更為明顯。

圖6和圖7分別為曲線梁橋上部結構在無控(NON-C)、經典線性最優控制(COC)以及序列最優控制算法(SOC)三種狀態下位移和加速度時變方差響應對比圖。

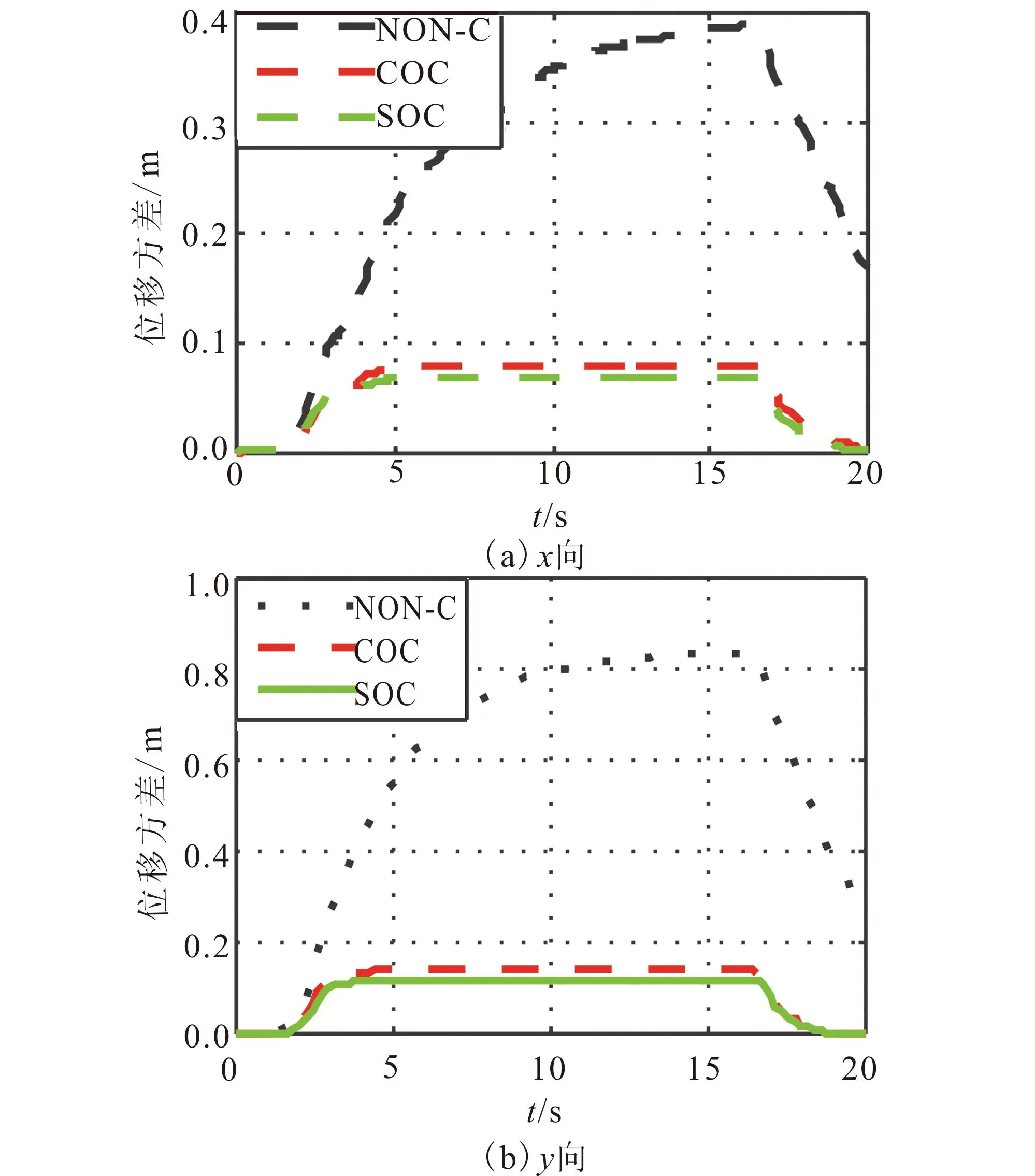
圖6　上部結構位移時變方差Fig.6The displacement time varying variance of superstructure

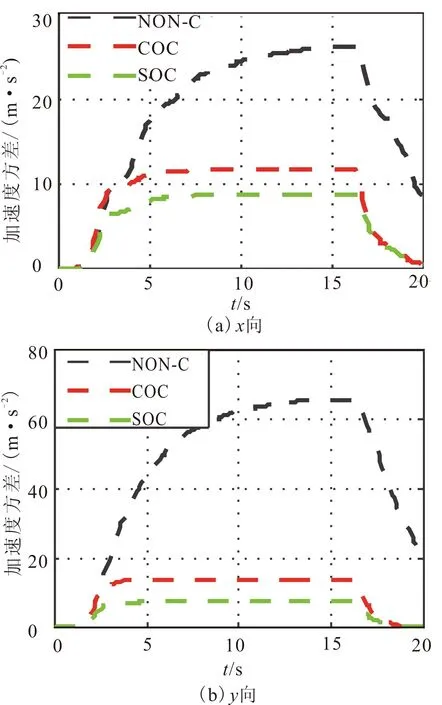
圖7　上部結構加速度時變方差Fig.7　The acceleration time varying variance of superstructure

由圖6、圖7可以看出，與無控狀態相比，兩種控制算法的位移和加速度時變方差響應都有明顯的降低。無論位移還是加速度的時變方差響應，序列最優控制算法(SOC)的效果更為明顯，尤其在降低上部結構加速度時變方差響應上且有更明顯的優勢。

4結論

本文對隔震曲線梁橋在無控(NON-C)、經典線性最優控制(COC)以及序列最優控制算法(SOC)三種狀態下的隨機反應進行了研究。研究結果表明：同無控結構相比，采用控制算法譜密度的響應及時變方差均明顯的降低，表明兩種算法都有很好的控制效果;在同等控制能量的條件下，序列最優控制算法(SOC)降低結構加速度功率譜響應的效果更為明顯，可以同時使上部結構的響應得到更有效的控制。

序列最優控制算法不需要求解Riccati方程，計算量小，沒有預先對目標函數引用近似簡化，僅有將地震波轉化為一系列脈沖和采用狀態轉移的數值算法的本身誤差。因此序列最優控制算法(SOC)從概念上更合理,可以取得更理想的減震效果。

參考文獻(References)

[1]亓興軍,申永剛.三維地震動作用下曲線連續梁橋減震控制研究[J].振動與沖擊, 2012,31(6):119-125.

QI Xing-jun,SHEN Yong-gang.Seismic Mitigation Control for a Curved Continuous Girder Bridge with 3-D Ground Motion Action[J].Journal of Vibration and Shock,2012,31(6): 119-125. (in Chinese)

[2]亓興軍,李小軍,唐暉.曲線橋彎扭耦合減震半主動控制分析[J].公路交通科技,2006,23(9):54-57.

QI Xing-jun,LI Xiao-jun,TANG Hui.Study on Semi-activecontrol of Seismic Bend Torsion Coupling for Curved Bridge[J].Journal of Highway and Transportation Research and Development,2006,23(9):54-57.(in Chinese)

[3]全偉,李宏男.曲線橋多維多點地震激勵半主動控制分析[J].工程力學,2009 (3): 79-85.

QUAN Wei,LI Hong-nan.Semi-active Control of Curved Bridge under Multi-component and Multi-support Earthquake[J].Engineering Mechanics,2009(3):79-85.(in Chinese)

[4]閻石,張海.高架橋地震反應半主動控制分析[J].地震工程與工程振動,2003,23(6):169-173.

YAN Shi,ZHANG Hai.Semi-active Vibration Control Analysis of Seismic Response for Elevated Highway Bridge Structures[J].Earthquake Engineering and Engineering Vibration, 2003,23(6):169-173.(in Chinese)

[5]歐進萍,王光遠.結構隨機振動[M].北京:高等教育出版社,1998.

OU Jin-ping,WANG Guang-yuan.The Random Vibration of Structure[M].Beijing:Higher Education Publishing Press,1998.(in Chinese)

[6]李慧,包超,杜永峰.近場地震作用下不規則層間隔震結構的動力響應分析[J].地震工程學報,2013,35(1):51-55.

LI Hui,BAO Chao,DU Yong-feng.Dynamic Response Analysis of Irregular Story Isolation Structures under Near-field Earthquake Conditions[J].China Earthquake Engineering Journal,2013,35(1):51-55.(in Chinese)

[7]李宏男,霍林生.結構多維減震控制[M].北京,科學技術出版社,2008.

LI Hong-nan,HUO Lin-sheng.Structural Multidimensional Vibration Control[M].Beijing: Science and Technology Publishing House,2008.(in Chinese)

[8]黨育.復雜隔震結構的分析與軟件實現[D].武漢：武漢理工大學,2011.

DANG Yu.Analysis and Software Development of Complex Isolated Buildings[D].Wuhan：Wuhan University of Technology,2011.(in Chinese)

[9]杜永峰,張尚榮,李慧.多級串聯非比例阻尼隔震結構地震響應分析[J].西北地震學報,2012,34(4):319-323.

DU Yong-feng,ZHANG Shang-rong,LI Hui.Seismic Response Analysis on Multistage Series Non-proportional Damping Isolation Structure[J].Northwestern Seismological Journal,2012,34(4):319-323.(in Chinese)

[10]杜永峰.被動與智能隔震結構地震響應分析及控制算法[D].大連：大連理工大學，2003.

DU Yong-feng.Analysis of Seismic Response of Passive and Smart Isolated Structures and Investigation to Control Algorithms[D].Dalian:Dalian University of Technology,2003.(in Chinese)

[11]Chi Y,Sain M K,Pham K D,et al.Structural Control Paradigms for an Asymmetric Building[C]//Proceedings of the 8thASCE Special Conference on Probabilistic Mechanics and Structural Reliability,PMC2000-152.

[12]杜永峰,李慧,趙國藩.地震作用下結構振動最優控制的一種一般算法[J].大連理工大學學報,2004,44(6):864-869.

DU Yong-feng,LI Hui,ZHAO Guo-fan.A General Algorithm of the Structure Vibration Optimal Control of Seismic Excitations[J].Journal of Dalian University of Technology 2004,44(6):864-869.(in Chinese)

[13]林家浩,張亞輝.隨機振動的虛擬激勵法[M].北京:科學出版社,2004.

LIN Jia-hao,ZHANG Ya-hui.The Random Vibration of the Pseudo Excitation Method[M].Beijing:Science Press,2004.(in Chinese)

[14]林治丹.考慮幾何非線性的串聯隔震體系隨機響應研究[D].蘭州：蘭州理工大學,2013.

LIN Zhi-dan.The Research on Random Vibration of the Serially Connected Isolation System[D].Lanzhou:Lanzhou University of Technology,2013.(in Chinese)

[15]汪夢甫.用虛擬激勵法求解非比例阻尼線性體系的非平穩隨機地震響應[J].力學季刊,2006,27(4):598-605.

WANG Meng-fu.Use Pseudo-excitation Method to Solve Non-Stationary Random Response of Non-Proportional Damped Systems[J].Chineses Quarterly of Mechanics,2006,27(4):598-605.(in Chinese)

[16]薛素鐸, 王雪生,曹資.基于新抗震規范的地震動隨機模型參數研究[J].土木工程學報,2003,36(5):5-10.

XUE Su-duo WANG Xue-sheng,CAO Zi.Parameter Study on Seismic Random Model Based on the New Seismic Code[J].China Civil Engineering Journal,2003,36(5):5-10.(in Chinese)

[17]李慧,王亞楠,杜永峰.平穩隨機地震激勵下TMD-基礎隔震混合控制體系的減震效果分析[J].合肥工業大學學報:自然科學版,2013,36(2):187-191.

LI Hui,WANG Ya-nan,DU Yong-feng.Effectiveness Analysis of TMD-base Isolation Hybrid Control System under Stationary Stochastic Seismic Excitation[J].Journal of Hefei University of Technology:Natural Science,2013,36(2):187-191.( in Chinese)

Vibration Control of Isolated Curved Girder Bridges under Nonstationary Seismic Excitation

LI Xi-mei1,2, DU Yong-feng1,2

(1.WesternEngineeringResearchCenterofDisasterMitigationinCivilEngineering,LanzhouUniv.ofTech.,Lanzhou730050,Gansu,China; 2.InstituteofEarthquakeProtectionandDisasterMitigation,LanzhouUniv.ofTech.,Lanzhou730050,Gansu,China)

Abstract：With the continuous development of structural seismic isolation technology, the use of seismic-isolation-device bridge designs is growing. The combination of isolation and additional damping devices is a commonly used method for controlling curved-beam bridges. Analyses of vibration control for research in the evaluation of seismic dynamic response have primarily focused on deterministic excitation, but deterministic earthquake excitation is not representative. In this study, we consider ground motion to be a uniformly modulated nonstationary random process and investigate long periods of low-frequency characteristics. Moreover, we select the Clough-Pension steady vibration power spectral model as a random vibration input for isolated curved bridges. To address the limitations of the classical optimal control algorithm, we derive vibration control equations using a sequential optimal control (SOC) algorithm. We then analyze the random responses of a curved bridge under three conditions: noncontrol, classical linear optimal control, and SOC algorithm. By establishing a curved beam bridge vibration equation of motion for random actions, we determine the displacement vibration control structure of the spectral density, acceleration spectral density response, and time variance. Analysis results show that the SOC algorithm can reduce the displacement of the isolation layer and more effectively control the seismic response of the upper structure, thus yielding a better control effect. The SOC algorithm has higher control performance and achieves better damping control.

Key words：curved bridges; sequential optimal control; pseudo excitation method; random response

DOI:10.3969/j.issn.1000-0844.2016.01.0103

中圖分類號:TU352.1； U441+.3

文獻標志碼：A

文章編號:1000-0844(2016)01-0103-06

作者簡介：李喜梅(1979-)，女，講師，主要從事橋梁減隔震及振控制研究。E-mail:mei611@163.com。

基金項目：甘肅省青年科技基金計劃(148RJYA008)；蘭州理工大學建工77基金(TMK-TJ-1001)

收稿日期：①2015-07-17

李喜梅1,2， 杜永峰1,2