應用馬爾科夫鏈計算藥物運轉時間和穩態藥量

劉愛紅, 楊 光

(沈陽師范大學 數學與系統科學學院, 沈陽 110034)

?

應用馬爾科夫鏈計算藥物運轉時間和穩態藥量

劉愛紅, 楊 光

(沈陽師范大學 數學與系統科學學院, 沈陽 110034)

考慮藥物在體內平均運轉時間和穩態藥量的計算及預測問題。首先,建立血管外給藥、靜脈注射n室模型,分別推導出每個模型下吸收馬爾科夫鏈的基本矩陣, 并對靜脈注射給藥方式,運用其基本矩陣的幾個基本性質計算藥物在體內的平均運轉時間;然后,將一個周期視為單位時間,在此單位時間下,依次重新改寫每個模型下吸收馬爾科夫鏈的基本矩陣;之后,給藥被認定是一個周期地向馬爾科夫鏈轉移部位的輸入過程,根據每次的給藥劑量給出輸入向量,并借助帶輸入的馬爾科夫鏈的一個基本性質預測兩模型下各房室內的穩態藥量;最后,運用3個數值模擬結果驗證該模型的有效性及可行性,為臨床藥型設計提供新的理論基礎。

馬爾科夫鏈; 基本矩陣; 運轉時間; 穩態藥量

0 引 言

馬爾科夫鏈是隨機過程中的重要概念之一,迄今為止,已被應用于多個領域,如:氣象預測、教學評價、人口預測、環境控制等,特別是在藥物動力學上也得到了一定的應用。實際上,藥物在體內的吸收、分布、消除過程符合吸收馬爾科夫鏈,因此,可以借助吸收馬爾科夫鏈來研究藥物在體內的運轉過程,本文將借此來估計各房室內的穩態藥量及藥物在體內的平均運轉時間。

對于穩態藥量、藥物在體內的運轉時間的研究,國內外已有大量相關文獻。其中,在計算穩態藥量方面,大多令給藥次數n→∞,將求取的極限藥量視為穩態藥量,但誤差較大;在估計藥物在體內的平均運轉時間問題上,已有文獻在血管外給藥模型下進行了估計[1],但還未考慮靜脈注射模型下的估計。

因此,本文將首先運用吸收馬爾科夫鏈的基本矩陣去估計藥物在體內的平均運轉時間;然后,考慮給藥是一個向吸收馬爾科夫鏈轉移部位的輸入過程,運用帶輸入的馬爾科夫鏈更精確地去估計各房室的穩態藥量;最后,通過模擬仿真去證明所建立的模型可行有效,為給藥策略的設計、臨床藥型設計提供更堅實的理論依據。

1 馬爾科夫鏈的基本矩陣

為確定靜脈注射、血管外給藥模型下的馬爾科夫鏈基本矩陣,作出如下假設:

[H1] 藥物在體內的運轉過程符合n室模型,且房室1是中央室,房室2～n是周邊室;

[H2]體外系統看做一個隔室,記為房室n+1;

[H3]對于血管外給藥方式,吸收部位看做一個隔室,記為房室0;

[H4]藥物僅在中央室進行消除過程;

[H5]周邊室僅與中央室之間具有轉運過程,各周邊室之間不能直接完成轉運過程;

[H6]房室i到房室j的轉移概率用轉運速率常數kij表示,特別的,房室0到房室1的轉移概率為吸收速率常數ka,房室1到房室n+1的轉移概率為消除速率常數k;

[H7]ka、k、kij的單位只取h-1或min-1;

[H8]ka、k、kij均取小于1的值,即:若已知kij=ah-1且a>1,則需令其先按如下方式換算:

本文考慮換算之后小于1的值。

[H9]在考慮周期性給藥時,將周期T作為單位時間。

事實上,對于血管外給藥模型,藥物在體內具有吸收、分布和消除過程,而對靜脈注射給藥模型,藥物直接進入到體循環,只有分布和消除過程,圖1和圖2分別描述了2種模型。

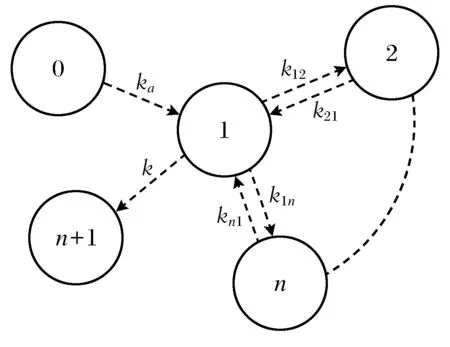
圖1 n室血管外給藥模型

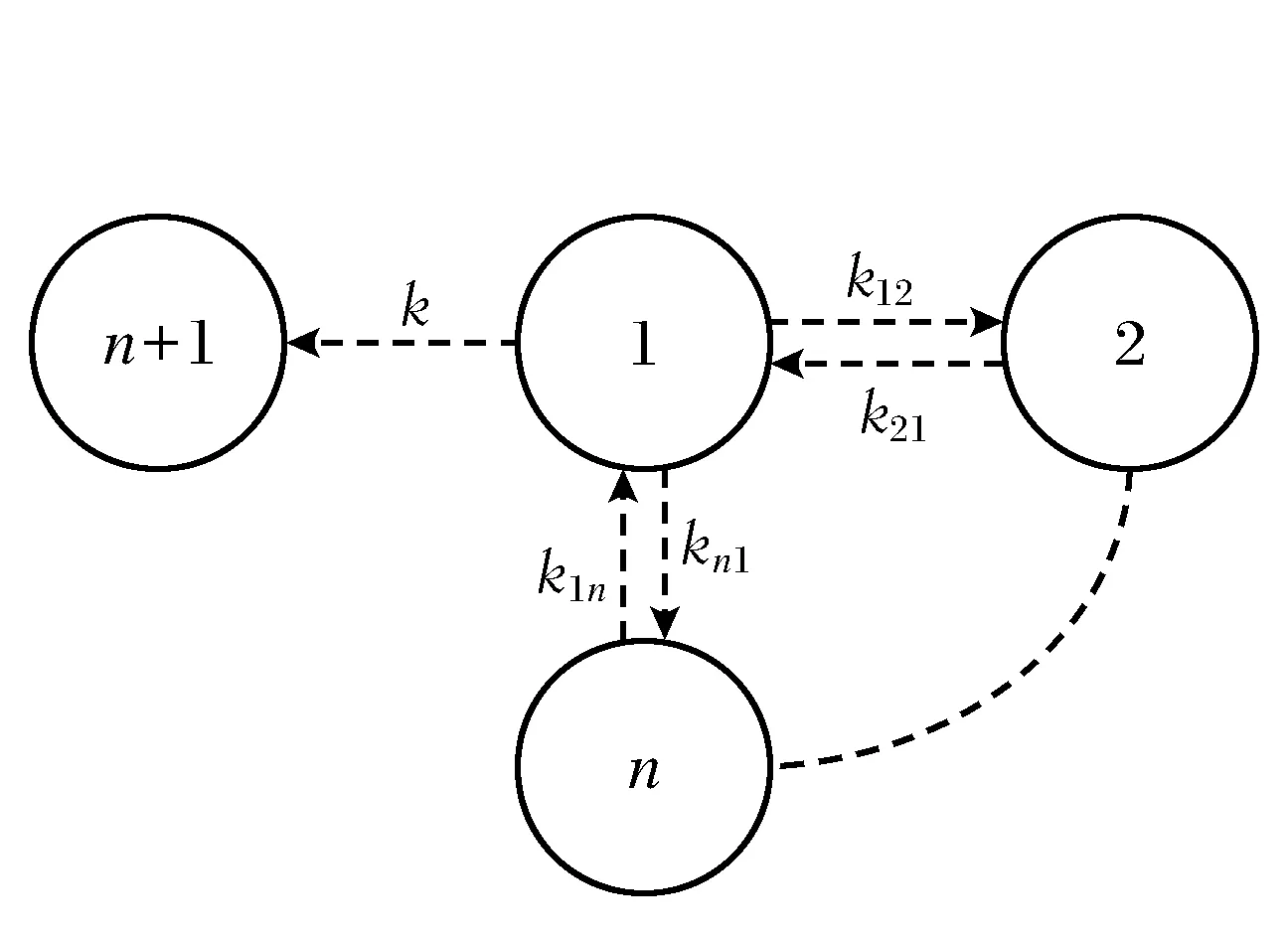
圖2 n室靜脈注射模型

定理1n室模型下馬爾科夫鏈的基本矩陣為

1) 血管外給藥模型下:

2) 靜脈注射模型下:

證明 1) N1已于文獻[1]給出。

2) 其對應的轉移矩陣P如下:

由此,

2 體內藥物平均運轉時間的估計

如上所述,對于血管外給藥模型,藥物在體內的運轉時間包括吸收、分布和消除3部分,而對靜脈注射給藥模型只有分布和消除2部分。它可以通過吸收馬爾科夫鏈的基本矩陣估計出來,其中血管外給藥模型下的平均運轉時間估計已由文獻[1]給出,因此本文僅考慮靜脈注射給藥模型。

定理2 對于適合靜脈注射的藥物,有如下結論:

1) 藥物在體內的平均運轉時間為

(1)

2) 藥物的消除時間為

(2)

證明 1)由文獻[2]中定理5.7及其推論、文獻[1]可知對于靜脈注射模型,N2的第i行元素之和為藥物從房室i開始,到達吸收狀態之前的平均運轉時間。由于靜脈注射給藥是一個脈沖過程,開始時藥物全部位于中央室,即房室1,然后逐漸消除或轉運,因此,藥物在體內的平均運轉時間是N2的第1行元素之和,計算即得式(1)。

2) 由于在房室1內,藥物只有消除過程,根據文獻[2]中定理5.7的推論可知:N2中第1行、第1列的元素為藥物的消除時間,即式(2)。

3 穩態藥量的估計

對于需要周期性給藥的藥物,隨著給藥次數的增加,體內藥物逐漸趨于穩定的水平,而穩定時的藥量也就是穩態藥量。

給藥可看作一個輸入過程,給藥量即為輸入量,且藥物輸入的部位在轉移狀態,因此給藥和藥物在體內的運轉2個過程可以看做是一個帶輸入的馬爾科夫鏈,故可運用帶輸入的馬爾科夫鏈來估計穩態藥量。下面首先給出吸收馬爾科夫鏈在n室模型下的定義。

定義1 在n室模型下,藥物在體內的運轉過程是一個具有n個轉移狀的吸收馬爾科夫鏈,單位時間向這n個狀態注入藥物,則構成了一個帶輸入的吸收馬爾科夫鏈,且輸入向量為

且有

注1 1) 可同時向多個轉移狀態輸入,即F中有多個非零元素;2)向不同轉移狀態的輸入量可以不同。

由于在帶輸入的馬爾科夫鏈中,考慮的輸入是單位時間的,且根據[H9]可知在本文中,對于周期性給藥方式,一個給藥周期被作為單位時間。下面將在這個基礎上改寫吸收馬爾科夫鏈基本矩陣并估計穩態藥量。

定理3 設某種藥物需周期性給藥,周期為Th(或min),則將一個周期作為單位時間時,吸收馬爾科夫鏈基本矩陣化為

(3)

證明 設k=ah-1,將一個周期(Th)作為單位時間,可將k作如下變換:

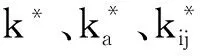
下面將在此基礎上,結合帶輸入馬爾科夫鏈的性質估計穩態藥量。

定理4 對于某種適合周期性給藥的藥物,給藥周期為Th(或min),每次給藥ng,則各房室內的穩態藥量Xss為

1) 對于血管外給藥方式:

(4)

其中,第i個元素表示房室i-1內的穩態藥量,i=1,2,3,…n+1。

2) 對于靜脈注射方式:

(5)

其中第i個元素表示房室i內的穩態藥量,i=1,2,3,…,n+1。

證明 1) 由圖1可知,房室n+1是吸收狀態,房室0～n是轉移狀態。單位時間(周期)地向房室0給藥,每次ng,則輸入向量為F=(n,0,0,…,0);

2) 由圖2可知,房室1～n是轉移狀態,房室n+1是吸收狀態。單位時間(周期性)地向房室1注射藥物,每次輸入ng,則輸入向量為

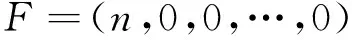
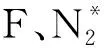
4 仿真模擬

1) 對某種需靜脈注射的雙室模型藥物,k=0.031min-1,k12=0.012min-1,k21=0.006min-1,則對應的吸收馬爾科夫鏈基本矩陣為

由于N2中第1行元素之和為96.78,所以該種藥物在體內的平均運轉時間為96.78min。

2) 某患者需要靜脈注射某種單室模型藥物,每6h注射一次,每次1g,且有k=0.231h-1,那么T=6h,且得到的輸入向量及馬爾科夫鏈基本矩陣為

3) 某患者需要口服某種雙室模型藥物,每4h服用一次,每次0.5g,并有如下參數:

ka=0.019min-1,k=0.005min-1,k12=0.001min-1,k21=0.002min-1,T=4h=240min,

則對應的輸入向量及基本矩陣依次為

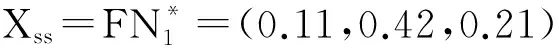
5 結 論

本文針對靜脈注射、血管外給藥2種方式分別確定了n室模型,并運用帶輸入的馬爾科夫鏈估計了各房室內的穩態藥量,借助吸收馬爾科夫鏈的基本矩陣估計了靜脈注射給藥方式下,藥物在體內的平均運轉時間,最后的仿真結果證明了模型的有效性,這可為藥物動力學的深入研究及臨床藥型設計提供更堅實的理論依據。

[1]丁勇. 用馬爾科夫鏈估算藥物在體內的平均轉運時間[J]. 數理統計與管理, 2009,28(4):751-755.

[2]徐克學. 生物數學[M]. 北京:科學出版社, 1999.

[3]梁文權. 生物藥劑學與藥物動力學[M]. 北京:人民衛生出版社, 2007.

[4]宋占杰,王家生,王勇. 隨機過程基礎[M]. 天津:天津大學出版社, 2011.

[5]張環環,周麗娟. 馬爾科夫鏈在通信市場3G用戶預測中的應用[J]. 廣西工學院學報, 2013,24(1):94-97.

[6]武漫漫,萬弢. 馬爾科夫鏈在天氣預報中的應用[J]. 黑龍江科技信息, 2009(30):58-59.

[7]孫艷蓉. 基于馬爾科夫鏈的人民幣匯率分析與預測[J]. 科技風, 2010(2):81-82.

[8]付長賀,鄧甦. 馬爾科夫鏈在傳染病預測中的應用[J]. 沈陽師范大學學報(自然科學版), 2009,27(1):28-30.

[9]丁明,徐寧舟. 基于馬爾可夫鏈的光伏發電系統輸出功率短期預測方法[J]. 電網技術, 2011,35(1):152-157.

[10]馬占青,徐明仙,俞衛陽,等. 年降水量統計馬爾科夫預測模型及其應用[J]. 自然資源學報, 2010,25(6):1033-1041.

Application of Markov chain in calculating operating time of drugs and dose in steady time

LIUAihong,YANGGuang

(School of Mathematics and Systems Science, Shenyang Normal University, Shenyang 110034, China)

This paper considers issues of calculating and forecasting the average operating time of drugs in vivo and dose in steady state. Firstly,n-compartment models of both intravenous injection and extravascular administration are established, fundamental matrix of absorbed Markov chain under each model is given respectively, and for intravenous injection dosing style, qualities of fundamental matrix are employed to calculate the average operating time of drugs in vivo; then, a period is seen as a unit time, under this unit time, the fundamental matrix under each model is rewritten successively; nextly, giving medicine is regarded as a periodic input process to transition position of Markov chain, input vector can be presented via dose given each time, a quality of Markov chain with inputs is applied to forecast dosage in steady state of each compartment under the two model; finally, results of three numerical simulations are utilized to show that this method is effective, feasible and being able to offer new theoretical foundations to clinical drug design.

input; Markov chain; fundamental matrix; operating time; dosage in steady state

2015-10-22。

遼寧省科技廳自然科學基金資助項目(2014020120); 遼寧省教育廳科學研究一般項目(L2013420)。

劉愛紅(1990-),女,遼寧北票人,沈陽師范大學碩士研究生; 通信作者: 楊 光(1964-),女,遼寧撫順人,沈陽師范大學教授,博士。

1673-5862(2016)01-0057-05

O212

A

10.3969/ j.issn.1673-5862.2016.01.013