關(guān)于三階三角樣條函數(shù)結(jié)構(gòu)的研究

, 葉學敏

(遼寧師范大學 數(shù)學學院, 遼寧 大連 116029)

?

理論與應用研究

關(guān)于三階三角樣條函數(shù)結(jié)構(gòu)的研究

(遼寧師范大學 數(shù)學學院, 遼寧 大連 116029)

近年來三角樣條的相關(guān)理論發(fā)展迅速,取得了豐碩的成果,但仍然存在一些問題,尤其是在均勻結(jié)點的三階三角樣條的結(jié)構(gòu)并不清晰。針對此問題,首先給出了均勻結(jié)點條件下的三階三角樣條函數(shù)的定義,這種三階三角樣條函數(shù)具有7個自由參數(shù),因而自由度更大。為了分析其結(jié)構(gòu),通過討論相鄰2段三角函數(shù)的二階光滑性限制條件,給出了關(guān)于這類樣條函數(shù)構(gòu)造的結(jié)構(gòu)定理,該定理表明相鄰一段三角樣條函數(shù)表達式可以表達為前一段三角樣條函數(shù)表達式與特定的帶參數(shù)的三階樣條函數(shù)之和,這為構(gòu)造具體三階三角樣條帶來了方便。還給出了有限多結(jié)點條件下此類樣條函數(shù)空間的維數(shù)定理。最后,通過結(jié)構(gòu)定理給出了幾個相關(guān)的例子。

三階三角樣條函數(shù); 三階三角樣條基; 維數(shù)

0 引 言

三角函數(shù)逼近的研究有著悠久的歷史,事實上,它與多項式逼近研究的進展是同步的。當有了Weierstrass關(guān)于[a,b]閉區(qū)間上連續(xù)函數(shù)的多項式逼近定理時,相應地就有了關(guān)于[-π,π]上的連續(xù)函數(shù)的三角多項式逼近定理。在有了多項式樣條后, 也有了三角多項式樣條。三角多項式樣條是1964年由 I.J.Schoenberg 最先提出并展開研究的[1],但他是用高階微分算子的方法切入的。文獻[2]是從構(gòu)造三階三角B-樣條基函數(shù)來展開討論的。文獻[3]利用3個函數(shù)值來構(gòu)造三次三角樣條函數(shù)。文獻[4-10]對三角樣條函數(shù)做了不同程度上的討論。本文研究三階三角多項式樣條,將其看作分片三角多項式來引入并展開研究。

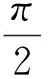
1 三階三角多項式樣條

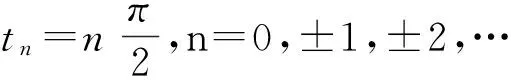
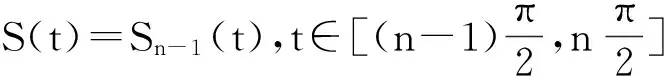
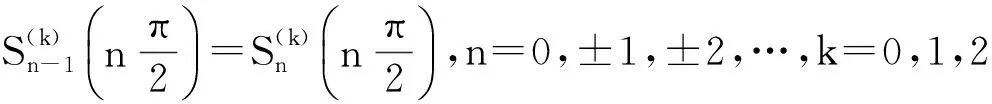
1) 首先考察S1(t)與S2(t)之間的關(guān)系。

3b2-2c2-f2=3b1-2c1-f1

9a2+4d2-e2=9a1+4d1-e1

即

解這個方程組得其基礎(chǔ)解系為以下4個解向量:

記η11=a2-a1,η12=b2-b1,η13=c2-c1,η14=d2-d1,η15=e2-e1,η16=f2-f1,η17=g2-g1,(η11,η12,η13,η14,η15,η16,η17)′=k11α11+k12α12+k13α13+k14α14，其中k11,k12,k13,k14是數(shù)域K中任意數(shù)。

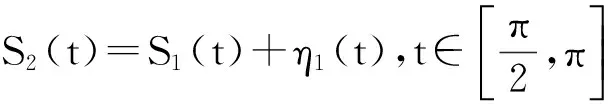
[1]FreemanTilden.Intepreting our heritage:University of North Crolina Press,1997,3（1）.

2) 用同樣的方法處理S2(t)與S3(t)之間的關(guān)系,得

其中:η2(t)=η21sin3t+η22cos3t+η23sin2t+η24cos2t+η25sint+η26cost+η27;(η21,η22,η23,η24,η25,η26,η27)′=k21α21+k22α22+k23α23+k24α24;α21=(0,3,0,8,0,5,0)′;α22=(2,0,3,0,0,0,0)′;α23=(-1,0,0,0,3,0,0)′;α24=(0,0,0,1,0,4,3)′,k21,k22,k23,k24是數(shù)域K中任意數(shù)。

3) 對于S3(t)與S4(t)之間的關(guān)系,有

其中:η3(t)=η31sin3t+η32cos3t+η33sin2t+η34cos2t+η35sint+η36cost+η37;(η31,η32,η33,η34,η35,η36,η37)′=k31α31+k32α32+k33α33+k34α34;α31=(0,5,0,0,0,15,0)′;α32=(0,0,5,0,0,10,0)′;α33=(-3,0,0,-8,5,0,0)′;α34=(4,0,0,9,0,0,5)′,k31,k32,k33,k34是數(shù)域K中任意數(shù)。

4) 對于S4(t)與S5(t)之間的關(guān)系,有

其中:η4(t)=η41sin3t+η42cos3t+η43sin2t+η44cos2t+η45sint+η46cost+η47,(η41,η42,η43,η44,η45,η46,η47)′=k41α41+k42α42+k43α43+k44α44;α41=(0,3,0,-8,0,5,0)′;α42=(-2,0,3,0,0,0,0)′;α43=(-1,0,0,0,3,0,0)′;α44=(0,0,0,1,0,-4,3)′,k41,k42,k43,k44是數(shù)域K中任意數(shù)。

正如前面所說,S5(t)與S6(t)之間的關(guān)系和S1(t)和S2(t)之間的關(guān)系完全相同。這樣,就得到三階三角樣條函數(shù)的結(jié)構(gòu)定理。

定理1 對于滿足條件的三階三角樣條函數(shù)S(t),有S(t)=Sn(t),n=0,±1,±2…,Sn(t)與Sn+1(t)之間滿足如下關(guān)系:

其中η4n+m(t),m=1,2,3,4的系數(shù)滿足如下關(guān)系:

(η4n+1,1,η4n+1,2,η4n+1,3,η4n+1,4,η4n+1,5,η4n+1,6,η4n+1,7)′=k4n+1,1α11+k4n+1,2α12+k4n+1,3α13+k4n+1,4α14,

(η4n+2,1,η4n+2,2,η4n+2,3,η4n+2,4,η4n+2,5,η4n+2,6,η4n+2,7)′=k4n+2,1α21+k4n+2,2α22+k4n+2,3α23+k4n+2,4α24,

(η4n+3,1,η4n+3,2,η4n+3,3,η4n+3,4,η4n+3,5,η4n+3,6,η4n+3,7)′=k4n+3,1α31+k4n+3,2α32+k4n+3,3α33+k4n+3,4α34,

(η4n+4,1,η4n+4,2,η4n+4,3,η4n+4,4,η4n+4,5,η4n+4,6,η4n+4,7)′=k4n+4,1α41+k4n+4,2α42+k4n+4,3α43+k4n+4,4α44,

k4n+i,j,i=1,2,3,4,j=1,2,3,4是數(shù)域K中任意數(shù)。

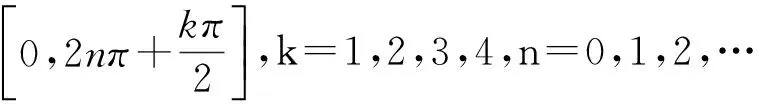
2 例 子

S4(t)=15sint+50cost+8cos2t-sin3t+14cos3t+20,S5(t)=

15sint+55cost-sin3t+17cos3t+20。

例3 已知在區(qū)間[0,π]上的三階三角樣條函數(shù)

當所有參數(shù)取1時的曲線及當kn,1=1/16,n=1,2,3,4,其他參數(shù)取0時的曲線在[0,π]上是一樣的,其他區(qū)間會根據(jù)參數(shù)的變化而變化。無論已知函數(shù)在哪個區(qū)間段,都能根據(jù)定理1構(gòu)造出后幾段函數(shù)。

3 結(jié) 論

本文討論了均勻節(jié)點意義下一般三階三角樣條函數(shù)的構(gòu)造及自然基的構(gòu)成,而已有文獻大多是從討論B-樣條基的構(gòu)造開始的。經(jīng)此校對知,在每2個樣條節(jié)點之間的區(qū)間上,構(gòu)成樣條函數(shù)的基函數(shù)都不是7個,這就是說,這些方法構(gòu)成的樣條函數(shù)空間都是本文所述的樣條函數(shù)空間的真子空間。

[1]SCHOENBERG I J. On trigonometric spline interpolation[J]. J Math Mech, 1964,13(5):795-825.

[2]HAN X. Cubic trigonometric polynomial curves with a shape parameter[J]. Comput Aided Geom D, 2004,21(6):535-548.

[3]吳曉勤, 韓旭里.C3連續(xù)的三角樣條函數(shù)與曲線[J]. 應用數(shù)學, 2001,14(增1):26-29.

[4]孫倩. 一類含參數(shù)均勻三角樣條及其插值曲線[D]. 合肥:合肥工業(yè)大學, 2006.

[5]HAN X. Quadratic trigonometric polynomial curves with a shape parameter[J]. Comput Aided Geom Des, 2002,19(7):503-512.

[6]翁祖蔭. 一階三角樣條[J]. 數(shù)學年刊A輯(中文版), 1983,4(2):185-190.

[7]劉曉雁. 一類二階三角樣條[J]. 合肥工業(yè)大學學報, 1985,7(1):33-38.

[8]王仁宏. 數(shù)值逼近[M]. 北京:高等教育出版社, 2005:220-243.

[9]王仁宏,李崇君,朱春剛. 計算幾何教程[M]. 北京:科學出版社, 2008:158-219.

[10]BURDEN R L, FAIRES J D. Numerical Analysis[M]. 北京:高等教育出版社, 2001:529-637.

Study of the structure of cubic trigonometric spline functions

WANGJingxin,YEXuemin

(School of Mathematics, Liaoning Normal University, Dalian 116029, China)

In recent years, the theory of trigonometric splines develops dramatically, and fruitful achievements have been made. However, some little information has been done on the structures of trigonometric splines. To solve this problem, we first propose the definition of cubic uniform trigonometric spline functions. This kind of splines has seven parameters in each interval which provide flexibilities in practical applications. To investigate the structures of proposed splines, we consider the second order continuity limitation imposed on two adjacent segments of trigonometric function, then we derive the structure theorem. This theorem demonstrates that the spline expression in each interval can be expressed as the sum of the previous cubic trigonometric function and one specific trigonometric function, which provide a more convenient approach in the design of trigonometric splines. Furthermore, we propose a dimension theorem of this kind of spline function with finite nodes. Finally, we give several related examples according to the structure theorem.

cubic trigonometric spline function; cubic trigonometric polynomial basis; dimension

2015-10-12。

國家自然科學基金資助項目(11226326)。

1673-5862(2016)01-0037-04

O241.5

A

10.3969/ j.issn.1673-5862.2016.01.009