基于鋼軌圖像頻域特征的鋼軌波磨檢測方法

李清勇, 章華燕, 任盛偉, 戴　鵬, 李唯一

(1.北京交通大學 交通數據分析與挖掘北京市重點實驗室, 北京　100044；2.中國鐵道科學研究院 基礎設施檢測研究所, 北京　100081)

鋼軌波浪形磨耗簡稱鋼軌波磨，是指鋼軌沿縱向表面出現的周期性的類似波浪形狀的一種不平順現象，是一種典型的軌頭表面缺陷[1]。長期以來，鋼軌波磨檢測大多采用專用卡尺進行人工抽樣測量，檢測效率低。近年來，研究人員提出了各種新型的鋼軌波磨檢測方法，主要包括弦測法、慣性基準法和機器視覺方法[1-3]。弦測法的基本原理是利用鋼軌上兩測點的連線作為測量弦，中間測點到該弦的垂直距離作為鋼軌波磨的測量值。慣性基準法的原理是計算加速度計安裝點相對慣性坐標系的位移，加速度計一般安裝在構架上，并在軸箱上安裝光電位移計，測量軸箱相對加速度計安裝點的位移[4]。隨著光電技術的發展，在弦測法或慣性基準法中，研究人員正在考慮采用光電攝像和圖像處理技術獲得位移信號，以提高檢測精度[5]。當前，基于計算機視覺的車載軌道巡檢系統在國內外都得到廣泛應用[6-9]，這些軌道巡檢系統能夠實時采集線路環境(包括軌道)的高分辨率數字圖像，然后運用先進的模式識別技術進行特定的后端處理。

相應地，基于機器視覺的鋼軌波磨檢測方法得到重視和應用。Mandriota等提出了基于空間濾波器特征和機器學習的鋼軌波磨檢測方法，該方法是目前常用的基于計算視覺的波磨檢測技術。該方法對整幅鋼軌圖像抽取Gabor紋理特征，然后應用K-近鄰方法進行波磨識別，取得了比較高的識別效果。但是該方法基于鋼軌圖像的全局特征，Gabor濾波速度比較慢，而且它還需要離線的模型訓練過程，使用不夠方便。

在前期工作[8, 10]的基礎上，本文提出了以局部頻率特征分析為核心的鋼軌波磨檢測方法。本文基于鋼軌圖像中縱向直線的頻域特性，提出基于累積能量閾值的波磨線(為鋼軌圖像中順軌方向的灰度值呈周期變化的直線)判定算法，然后對局部的波磨線判定結果進行全局整合，最后識別輸入圖像是否包含波磨。

1　基于頻域特性的鋼軌波磨檢測算法

在巡檢系統采集的圖像中鋼軌波磨體現為明暗相間的周期模式。如果把圖像按列進行傅里葉變換，那么鋼軌的波磨線在頻域上的能量分布具有明顯的稀疏性，并且波磨線的能量集中在低頻的區間。由此本文提出了基于頻域特征的鋼軌波磨檢測算法，該算法包括4個主要的步驟(如圖1所示，圖1(d)中黑線標識的區間為鋼軌波磨區間)。

(1)鋼軌定位。根據軌道圖像中鋼軌區域和背景區域的灰度統計特征差異，提出了基于位置加權灰度垂直投影分析的鋼軌定位算法。該算法能夠去除背景區域對于后續過程的干擾，快速有效地提取鋼軌圖像。

(2)傅里葉變換。對鋼軌圖像按列進行傅里葉變換，把鋼軌圖像從空間域轉換到頻率域。

(3)波磨線判定。對鋼軌圖像中的每一列，分析其傅里葉變換系數，根據占優頻率的位置和能量識別該列是否屬于波磨線。

(4)鋼軌波磨區間判定。鋼軌波磨一般由1組連續的波磨線構成，對于鋼軌圖像的每一列進行判定后，再對鋼軌圖像進行區間分析，識別是否存在符合要求的波磨區間。

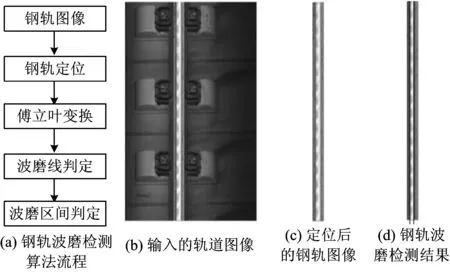
圖1　波磨檢測算法示意圖

1.1　鋼軌的定位

在軌道圖像中，鋼軌所在區域的灰度值一般比較高，而背景部分區域的灰度值比較低。基于此規律，文獻[10]提出了平均灰度投影算法。該方法在理想情況下能準確定位鋼軌，但是當鋼軌有嚴重銹跡，或者有強烈外界光源影響時，采用該方法進行鋼軌定位就會出現錯誤。

通過分析大量軌道圖像后發現，軌道圖像呈現以下明顯的結構和統計特征：①鋼軌區域在順軌方向的灰度均值比較大；②鋼軌兩側的背景區域是扣件或軌枕等部件，其灰度方差比較大，而鋼軌區域的灰度方差比較小；③在軌檢車的圖像采集設備安裝好之后，在它采集的軌道圖像中，鋼軌部件的位置是大致確定的，一般位于軌道圖像的中間區域。

因此，提出了改進的鋼軌定位(Improved Track Localization, ITL)算法。ITL算法首先計算軌道圖像每一列的灰度均值與灰度方差的比值，然后將該比值乘以1個位置權重，得到該列的特征值；組合軌道圖像每一列的特征值，得到其特征值向量，然后搜索特征值之和最大的定長區間即為鋼軌區域。

假設I(x,y)為軌道圖像I中坐標(x,y)處的灰度值，則軌道圖像第x列的特征值g(x)為

(1)

其中，

式中：b0為軌道圖像I的寬度；μ和δ分別為高斯函數的均值和標準差，因為鋼軌一般位于軌道圖像的中間，所以μ取b0/2，δ經過試驗取為16。

需要注意的是，當圖像采集設備設定好后鋼軌圖像的寬度也是固定的，記為常數b。根據式(1)得到特征值向量G=(g(1),g(2), …,g(b0))，則鋼軌的位置T為

(2)

其中，

式中：Sg(p)為特征值向量G中從位置p開始長度為b的所有特征值之和。

根據平均灰度投影算法(傳統方法)和ITL算法(改進算法)得到的鋼軌定位結果如圖2所示。圖中：虛線所示為采用傳統方法得到的結果，實線為采用改進算法得到的結果。

圖2　鋼軌定位方法對比實例

由圖2可見：采用傳統方法定位鋼軌圖像時，因為上方有強烈的外界光照，該方法錯誤地將鋼軌定位在虛線區域；而改進算法較準確地定位了鋼軌圖像。

1.2　波磨線的判定

通過ITL算法提取鋼軌圖像后，需要分析鋼軌圖像每一列的頻域特征，并且判定其是否為波磨線。波磨線判定包括2個步驟：首先對圖像列進行傅里葉變換，然后根據其頻域特征判定該列是否為波磨線。

假設輸入的鋼軌圖像為IR，其寬度記為b，高度記為h。對圖像IR中的第x列進行傅里葉變換，其傅里葉變換系數Fx(m)為

(3)

式中：m為頻率，m∈[0，h-1]。

Fx(m)是一個復數， 波磨判定算法主要關注的是其能量譜和頻率特性， 因此， 需要計算Fx(m)的模， 記為E(m)。因為實數序列傅里葉變換的系數是對稱的，為了便于計算，所以只考慮Fx(m)的前半部分，并且對其能量譜即模E(m)進行歸一化處理，得到

(4)

式中：EN(m)為歸一化的能量值，EN(m)∈[0, 1]。

需要注意的是，直流分量E(0)等于平均灰度，它受光照的影響比較大，因此在歸一化時沒有考慮它。

傅里葉變換性質表明任意一個函數都可以表示為不同周期的正弦函數的線性加權和，而且傅里葉變換系數的模E(m)體現了頻率為m的正弦函數的重要程度。因此，如果鋼軌圖像IR某一行的灰度值呈現出明顯的周期性的波動，說明特定頻率的正弦函數的重要程度高，而其他頻率的正弦函數貢獻相對較小。

圖3展示了1個典型的波磨線和背景直線的灰度曲線和能量譜分布曲線。由圖3可見：波磨線灰度曲線的周期性比較明顯，且在能量譜分布中低頻區間存在明顯的峰值；而背景直線的灰度曲線則無明顯周期性，且其能量譜分布非常分散，也沒有明顯波峰。因此，將能量譜的波峰信息作為波磨線判定的依據。

定義能量譜分布中波峰對應的頻率為占優頻率(Dominant Frequency)，記為f，則第x行的占優頻率fx可以定義為

m∈[1,h/2]

(5)

式中：t1為能量譜的閾值，是外部輸入參數。

圖3　鋼軌圖像中典型波磨線和背景直線的灰度曲線和能量譜曲線

需要注意的是，并不是所有的波峰都對應占優頻率，但其歸一化能量值必須大于特定的閾值。

占優頻率可以推導出3個判定波磨線的特征，它們分別是頻率值D，歸一化能量EN以及累積能量(Accumulated Energy)EA。鋼軌圖像第x行的累積能量EA為

(6)

在手工標注1 000條波磨線和背景直線的基礎上，對波磨線的上述3個特征進行了統計分析，圖4給出了統計分析結果。由圖4可見：背景直線的占優頻率主要集中在超低頻區間，其值絕大部分都小于5；而波磨線的也主要集中于低頻區間，但其值絕大部分在5～35之間；背景直線占優頻率的能量值主要在0.01以下，而典型波磨線占優頻率的能量值分布卻更加分散一些；背景直線的累積能量偏小，而波磨線的則往往比較大。

根據以上這些特征值的統計結果，提出了2種波磨線判定算法：頻率閾值法和累積能量閾值法。

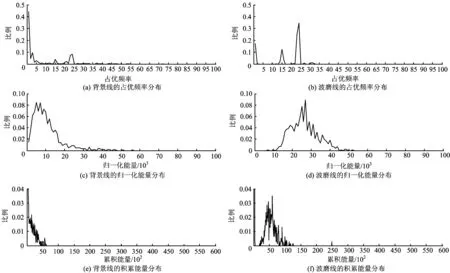
圖4　鋼軌圖像占優頻率特征值的統計分析結果

1)頻率閾值法(Frequency Thesholding, FT)

計算出鋼軌圖像IR的第x列的占優頻率fx后，如果占優頻率存在而且處于指定的低頻區間，則判定鋼軌圖像的第x列為波磨線，其判定函數r(x)為

(7)

式中：fmin和fmax分別為占優頻率的下限和上限，均為外部輸入參數。

在式(7)中，r(x)等于1時代表波磨線，等于0時代表背景線。如果鋼軌圖像第x列不存在占優頻率，則直接判定該列為背景線。

2)累積能量閾值法(Accumulate Energy Thresholding, AET)

基于累積能量判定鋼軌圖像的波磨線，它綜合考慮頻率和能量2個方面的因素。假定鋼軌圖像IR的第x列的占優頻率fx存在，其累積能量為EA，則判定函數為

(8)

式中：t2為閾值，且為外部輸入參數。

1.3　波磨區間的判定

波磨區間的判定是波磨檢測的最后過程，它綜合鋼軌圖像每一列的波磨線判定結果，形成整體的識別結果。單個波磨線可能是偶然現象，或者是由噪聲引起的誤判。只有當存在連續的若干條波磨線時，檢測算法才能確定這是一個波磨區間。

組合每一列的波磨線判定結果，可以得到結果向量R為

R=(r(1),r(2), …,r(b))

(9)

顯然R是b維的、取值為0～1的向量，搜索結果向量中最大的連續區間，其長度記為l。則判定鋼軌圖像波磨區間的函數c為

(10)

式中：t3為外部輸入參數，其具體的值與圖像采集模塊的設置以及線路性質有關。

按照式(10)，當連續波磨線的長度大于指定閾值t3時，判定鋼軌圖像為波磨圖像，即c=1；否則為非波磨圖像，有c=0。

2　試驗結果及分析

本文試驗的數據都來自運營線路上實際采集的軌道圖像。圖像采集設備安裝在軌檢車的車廂底部，圖像采集系統包括Dalsa黑白線陣攝像機、Camlink高速圖像采集卡和LED 光源等部件。相機最高行掃描頻率為65 kHz, 全視野1 024像素, 縱向和橫向采樣分辨率為1 mm。專業人員從多條線路的軌道圖像中篩選出200幅典型波磨圖像作為測試的正樣本，另外隨機選擇200幅非波磨圖像作為負樣本。

檢測算法的性能采用精準率Pre，召回率Rec和正確率Acc這3個指標來評價，分別為

(11)

(12)

(13)

式中：Tp為被正確檢測到的波磨圖像數目；Fn為被漏檢的波磨圖像數目；Fp為被誤報為波磨的圖像數目；Tn為被正確排除的非波磨圖像數目。

2.1　波磨線的判定性能評估

波磨線的判定是整個檢測算法的核心，本節對提出的FT算法和AET算法進行性能對比試驗。在本試驗中，試驗人員事先人工標定出1 000條典型波磨線和1 000條背景直線，得到采用不同算法得到的精準率、召回率和正確率，其結果見表1。其中FT算法的閾值下限fmin=6，閾值上限fmax=35,AET算法的閾值t3=1.0。表1結果表明：AET算法比FT算法的精準率、召回率和正確率都有一定程度的提高；另外需要指出的是，AET算法只需要1個輸入參數，而FT算法則需要2個輸入參數，即AET算法更簡便。

表1　采用FT與AET算法時的波磨線判定性能比較

為了更加細致地比較FT和AET算法的性能差異，我們分析了它們的P—R曲線圖，如圖5所示。P—R曲線為由不同參數條件下計算得到的Pre和Rec值所構成的曲線，它詳細描述了算法的檢測性能。一般地，P—R曲線與坐標軸包圍的面積越大，其性能就越好。由圖5可見：在精準率相同的條件下，由AET算法計算得到的召回率優于FT算法。

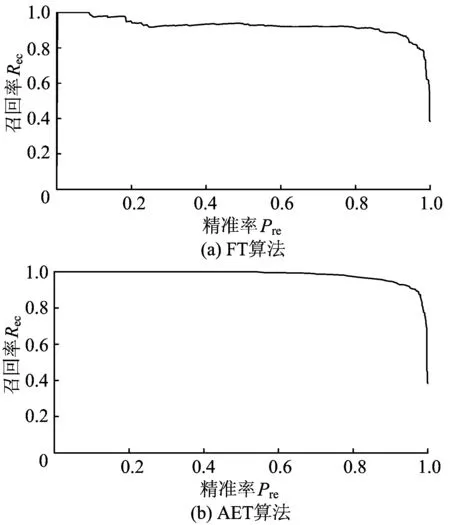
圖5　由FT與AET算法得到的P—R曲線圖

總之，AET算法比FT算法的檢測性能更好，魯棒性更強。

2.2　波磨區間的判定性能評估

為與Mandriota等[6]提出的傳統方法(包括Gabor+SVM法和Gabor+KNN法)比較，采用了8維的Gabor濾波器特征，所有參數與原文保持一致，KNN采用留一法進行分類訓練與預測，SVM采用十折交叉驗證法進行分類訓練與預測。

傳統方法與本文方法的比較結果見表2。由表2可見：本文方法在3個指標上都優于傳統方法，尤其是召回率提高非常明顯，超過了11%，召回率是3個指標中最重要的指標，召回率高意味著漏檢的波磨圖像少；本文方法的檢測速度也遠遠高于傳統方法；另外需要指出的是，本文方法不需要進行離線的模型訓練，使用更加方便。

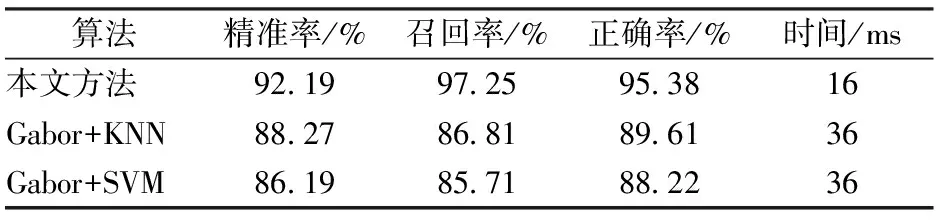
表2　本文方法與傳統方法的比較

占優頻率是本文方法的關鍵要素。其他參數保持最優設置不變，只改變占優頻率定義中的閾值t1，得到檢測算法3個性能指標的變化情況，如圖6所示。由圖6可見：在t1小于0.02時，3個性能指標都比較理想，均在90%以上；當t1增大時，精準率略有提高，但是召回率和正確率都快速下降，這是因為t1增大時，只有周期性非常明顯的波磨線被正確識別，而大部分波磨線都可能漏判；極端情況時，所有列都判定為非波磨線，進而所有圖像都判定為非波磨圖像，導致召回率為0，正確率為50%。

3　結　語

(1)在分析軌道圖像和鋼軌波磨形態學特征的基礎上，提出了基于圖像頻域特征的鋼軌波磨檢測方法。該方法首先改進了傳統的鋼軌定位算法，提出了位置加權的鋼軌定位算法；然后，基于鋼軌圖像的傅里葉系數特征，設計了基于頻率閾值和基于累積能量閾值的2種波磨線判定方法；最后，識別連續波磨區間大于指定閾值的圖像為波磨圖像。

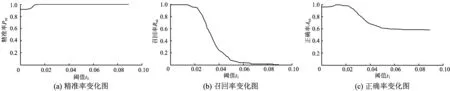
圖6　閾值t1對于檢測算法性能指標的影響

(2)采集實際運營線路的圖像進行檢測方法的性能測試，結果表明本文方法的精準率和召回率分別為92.19%和97.25%，比現有方法提高了約4%和11%，同時，檢測速度提高了1倍以上。

(3)下一步工作主要應進行以下幾個方面的研究。首先，考慮波磨線判定方法的并行化，進一步提高檢測速度；其次，應用機器學習模型改善算法的自適應性；最后，工程化并部署到當前的軌道巡檢系統上，大規模地測試和驗證算法性能。

[1]OOSTERMEIJER K H. Review on Short Pitch Rail Corrugation Studies [J]. Wear, 2008， 265(9/10): 1231-1237.

[2]SATO Yoshihiko, MATSUMOTO Akira, KNOTHE Klaus. Review on Rail Corrugation Studies [J]. Wear, 2002(253): 130-139.

[3]姜子清, 司道林, 李偉, 等. 高速鐵路鋼軌波磨研究[J].中國鐵道科學, 2014, 35(4): 9-15.

(JIANG Ziqing, SI Daolin, LI Wei, et al. On Rail Corrugation of High Speed Railway [J]. China Railway Science, 2014, 35(4): 9-14. in Chinese)

[4]劉伶萍, 杜鶴亭, 楊愛紅. 鋼軌波浪磨耗檢測系統的研究開發[J]. 中國鐵道科學, 2002, 23(6): 65-69.

(LIU Lingping, DU Heting, YANG Aihong. Development of Rail Corrugation Inspection System[J]. China Railway Science, 2002, 23(6): 65-69. in Chinese)

[5]鄭樹彬，柴曉冬，安小雪，等. 基于動態模板的鋼軌磨耗測量方法研究[J]. 中國鐵道科學, 2013, 34(2):7-13.

(ZHENG Shubin, CHAI Xiaodong, AN Xiaoxue, et al. Rail Wear Measuring Method Based on Dynamic Template [J]. China Railway Science, 2013, 34(2):7-13. in Chinese)

[6]MANDROTA C, NITTI M, ANCONA N, et al. Filter-Based Feature Selection for Rail Defect Detection [J]. Machine Vision and Applications, 2004, 15(4): 179-185.

[7]許貴陽,史天運,任盛偉,等.基于計算機視覺的車載軌道巡檢系統研制[J].中國鐵道科學,2013,34(1):139-144.

(XU Guiyang, SHI Tianyun, REN Shengwei, et al. Development of the On-Board Track Inspection System Based on Computer Vision [J]. China Railway Science, 2013, 34(1): 139-144. in Chinese)

[8]LI Q, REN S. A Real-Time Visual Inspection System for Discrete Surface Defects of Rail Heads [J]. IEEE Transactions on Instrumentation and Measurement, 2012, 61(8): 2189-2199.

[9]MARINO F, DISTANTE A, MAZZEO P L, et al. A Real-Time Visual Inspection System for Railway Maintenance: Automatic Hexagonal-Headed Bolts Detection [J]. IEEE Transactions on Systems Man and Cybernetics Part C: Applications and Reviews, 2007, 37(3): 418-428.

[10]任盛偉, 李清勇, 許貴陽, 等. 魯棒實時鋼軌表面擦傷檢測算法研究 [J]. 中國鐵道科學, 2011, 32(1): 25-29.

(REN Shengwei, LI Qingyong,XU Guiyang, et al. Research on Robust Fast Algorithm of Rail Surface Defect Detection [J]. China Railway Science, 2011, 32(1): 25-29. in Chinese)