粗糙度對(duì)離心泵泥沙磨損特性的影響分析

蘇佳慧，董 靜，錢忠東，郭志偉

(武漢大學(xué) 水資源與水電工程國(guó)家重點(diǎn)實(shí)驗(yàn)室，武漢 430072)

我國(guó)的許多灌區(qū)都是以黃河水作為灌溉水源，但黃河水流含沙量很高，使得水泵的磨損問(wèn)題非常嚴(yán)重。泥沙磨損會(huì)導(dǎo)致水泵揚(yáng)程，流量，效率大幅度下降，運(yùn)行功率增加，運(yùn)行可靠性降低，水泵的高效和安全運(yùn)行得不到保證。因而泥沙磨損一直是水泵研究的重點(diǎn)。

已有的研究表明，壁面粗糙度會(huì)對(duì)水泵的性能產(chǎn)生顯著的影響。鄭槐卿[1]通過(guò)試驗(yàn)得到了適合計(jì)算離心泵流道表面粗糙度對(duì)效率影響的公式；談明高、劉厚林[2]等研究了粗糙度對(duì)離心泵性能數(shù)值預(yù)測(cè)的影響；李龍，王澤[3]研究了粗糙度對(duì)軸流泵水力性能的影響。目前，有關(guān)粗糙度的研究多是清水工況，對(duì)于抽送含沙水流時(shí)，壁面粗糙度對(duì)離心泵的影響，相關(guān)的研究較少。

目前計(jì)算流體力學(xué)(CFD)方法對(duì)水泵性能預(yù)測(cè)的結(jié)果已達(dá)到工程應(yīng)用精度，因此本文對(duì)雙吸式離心泵采用數(shù)值模擬的方法[4]，綜合研究壁面粗糙度及含沙水流對(duì)雙吸式離心泵的影響。

1 計(jì)算模型

計(jì)算采用的雙吸式離心泵模型如圖1所示，計(jì)算區(qū)域包括進(jìn)水流道、半螺旋形吸入室、葉輪部分、蝸殼壓水室、出水流道。計(jì)算模型以250S-14雙吸式離心泵為原型泵，設(shè)計(jì)工況下?lián)P程14 m，額定轉(zhuǎn)速1 450 r/min，葉片數(shù)6片。葉輪直徑為244 mm，進(jìn)出水流道管徑250 mm，進(jìn)出水流道長(zhǎng)度均為5倍管徑。

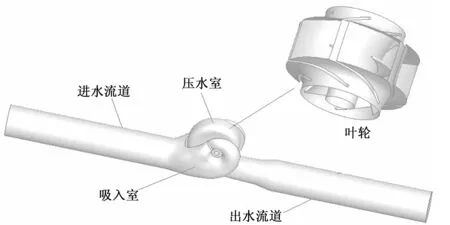
圖1 雙吸式離心泵三維模型圖

表面粗糙度是指加工表面具有的較小間距和微小峰谷的不平度。表面粗糙度越小，表面越光滑。按照現(xiàn)有的加工制造水平，實(shí)際生產(chǎn)的水泵壁面粗糙度高低不一，錯(cuò)落分布，表面結(jié)構(gòu)比較復(fù)雜，粗糙元一般具有各種形狀與尺寸，且隨機(jī)分布，很難對(duì)其進(jìn)行準(zhǔn)確的描述，由于計(jì)算軟件自身的局限性，不可能完全真實(shí)地反映實(shí)際的粗糙狀況，因此，本文對(duì)實(shí)際情況進(jìn)行了簡(jiǎn)化，認(rèn)為壁面分布有均勻的粗糙元，以此來(lái)初步探究一種理想的壁面粗糙狀況對(duì)雙吸式離心泵泥沙磨損的影響機(jī)理。在Fluent文件中，壁面粗糙狀況如圖2所示。

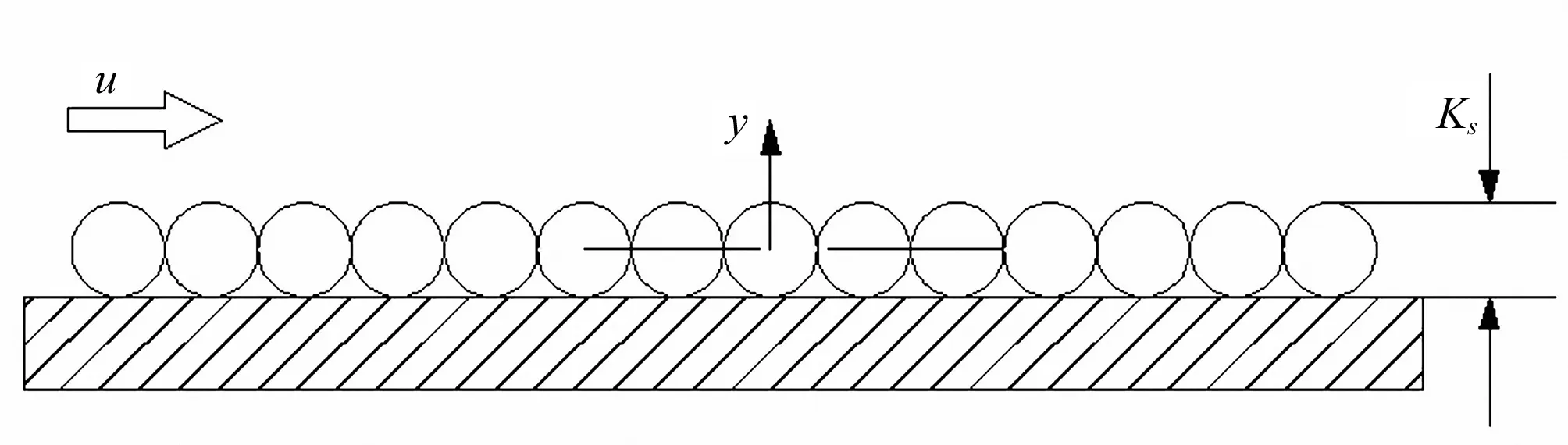
圖2 均勻沙粒粗糙元分布

2 控制方程

離心泵內(nèi)的流動(dòng)為湍流流動(dòng)，湍流流動(dòng)隨時(shí)間和空間呈現(xiàn)不規(guī)則的脈動(dòng)，因此在計(jì)算時(shí)引入了湍流模型，假定湍流中的流場(chǎng)變量由一個(gè)時(shí)均量和一個(gè)脈動(dòng)量組成，將瞬態(tài)Navier-Stokes方程雷諾平均得到雷諾時(shí)均方程(RANS)。

連續(xù)方程：

(1)

動(dòng)量方程：

(2)

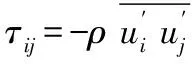
由于方程中增加了未知的雷諾應(yīng)力項(xiàng)τij，方程不封閉，因而引入湍流封閉模型。半螺旋形吸入室、蝸殼壓水室以及葉輪的旋轉(zhuǎn)使得雙吸式離心泵內(nèi)存在強(qiáng)烈的旋流，而標(biāo)準(zhǔn) 模型在計(jì)算強(qiáng)旋流時(shí)與實(shí)驗(yàn)結(jié)果偏離較大[5]，因此文章采用可靠性更高的RNGk-ε模型[6]。Reynolds應(yīng)力表示為：

(3)

在高雷諾數(shù)時(shí)，湍動(dòng)黏性系數(shù)表示為：

(4)

式中：k表示湍動(dòng)能；ε為耗散率。

對(duì)于RNGk-ε模型，k與ε由以下兩個(gè)輸運(yùn)方程得來(lái)。

湍動(dòng)能方程：

(5)

耗散率方程：

(6)

式中：C1ε=1.42，C2ε=1.68，Cμ=0.084 5，αk=αε=1.393；Gk是指由平均速度梯度產(chǎn)生的湍動(dòng)能；Gb是指由浮力產(chǎn)生的湍動(dòng)能；YM是可壓縮湍流流動(dòng)產(chǎn)生的膨脹脈動(dòng)對(duì)耗散率的影響；Sk和Sε為用戶自定義項(xiàng)。

歐拉-拉格朗日多相流模型可以準(zhǔn)確的模擬顆粒在連續(xù)相中的運(yùn)動(dòng)，模型中的顆粒運(yùn)動(dòng)方程為：

(7)

磨損速率方程為：

(8)

3 邊界條件與計(jì)算方法

本文的計(jì)算工況采用設(shè)計(jì)工況，按照水泵實(shí)際運(yùn)行時(shí)的測(cè)量數(shù)據(jù)設(shè)定邊界條件。設(shè)置固定進(jìn)口流量與出口壓力。進(jìn)口斷面質(zhì)量流量134.5 kg/s，出口壓力137.303 3 kPa。計(jì)算時(shí)認(rèn)為離心泵內(nèi)的流體不可壓縮，計(jì)算中不考慮重力對(duì)流場(chǎng)的影響。近壁區(qū)處理采用標(biāo)準(zhǔn)壁面函數(shù)，壁面邊界條件采用無(wú)滑移條件，葉輪各壁面采用旋轉(zhuǎn)的參考坐標(biāo)并設(shè)定旋轉(zhuǎn)速度相對(duì)流域旋轉(zhuǎn)速度為0。離散相沖擊磨損模型設(shè)置為顆粒隨機(jī)軌道模型，通過(guò)給定顆粒隨流體流入的質(zhì)量流量來(lái)考慮水流中所有粒子的影響。設(shè)置單一濃度，單一粒徑的顆粒進(jìn)行模擬計(jì)算，著重研究泵在低濃度、小粒徑泥沙作用下的磨損狀況。設(shè)置顆粒粒徑0.02 mm，質(zhì)量流量1.35 kg/s。

壓力-速度耦合采用收斂速度較好的SIMPLEC算法，方程離散采用有限體積法，離散后的方程采用Green-Gauss Cell Based方法計(jì)算梯度，PRESTO格式計(jì)算壓力方程，QUICK格式計(jì)算動(dòng)量方程，一階迎風(fēng)差分格式計(jì)算湍動(dòng)能方程、耗散率方程。

4 計(jì)算結(jié)果與分析

普通新鑄鐵的當(dāng)量粗糙度約為0.3 mm[7]。本文設(shè)置壁面粗糙度Ks=0.1、0.2、0.3、0.5、0.75 mm，分別計(jì)算以下3種情況時(shí)壁面粗糙度對(duì)模型泵的影響：A,同時(shí)改變水泵所有部件的粗糙度；B,只改變?nèi)~片以外所有部件的粗糙度；C,只改變?nèi)~片的粗糙度。圖3和圖4為離心泵揚(yáng)程、效率隨壁面粗糙度變化的關(guān)系曲線。

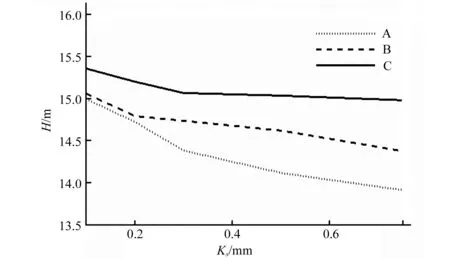
圖3 揚(yáng)程變化曲線圖

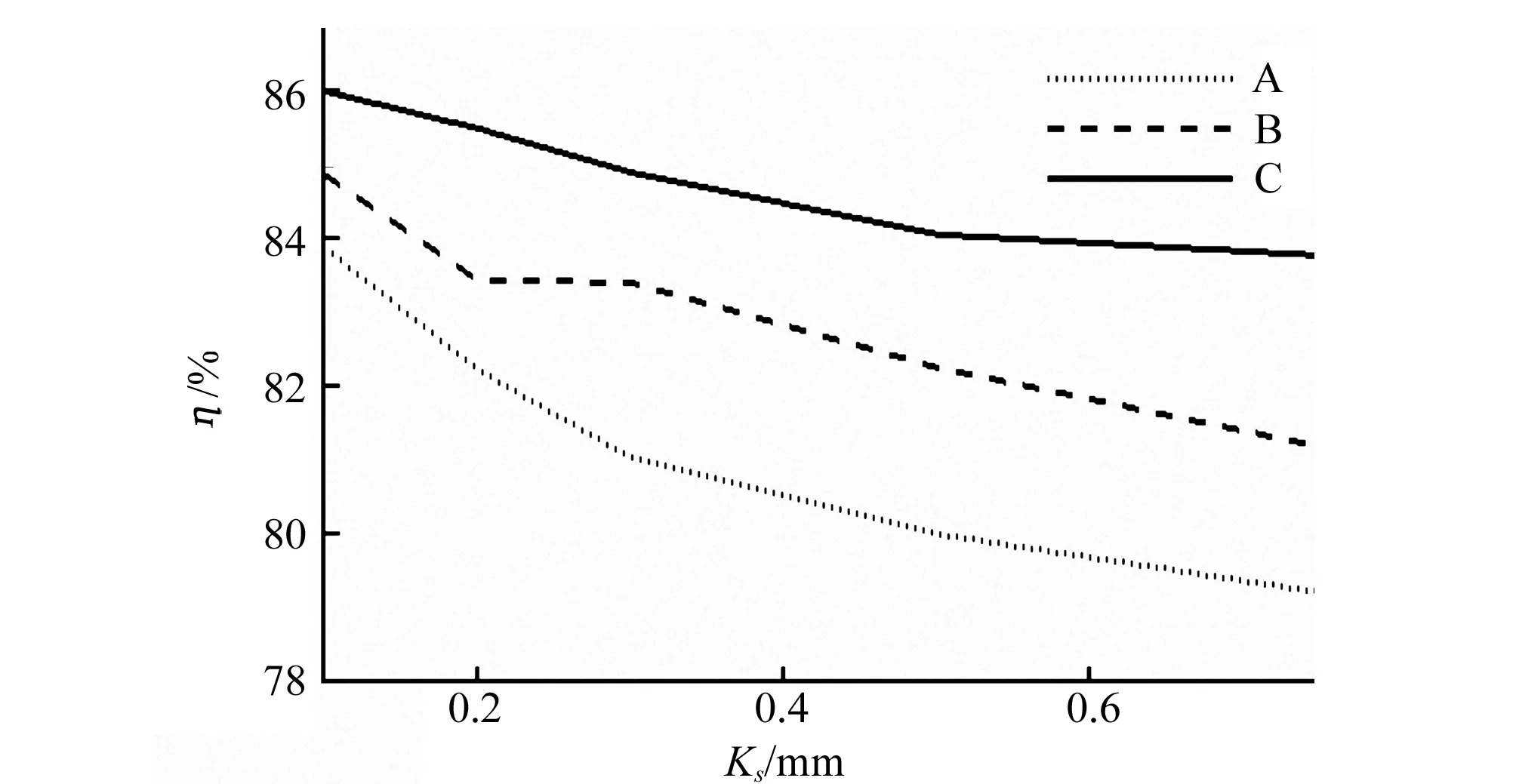
圖4 效率變化曲線圖

從圖3和圖4可以看出，隨著粗糙度的增大，水泵的揚(yáng)程、效率都在下降。小粗糙度時(shí)下降速度較快，大粗糙度時(shí)下降速度減緩。同時(shí)，對(duì)比A、B、C 3種情況對(duì)應(yīng)的曲線，發(fā)現(xiàn)A下降最快，B次之，C最緩，綜合考慮所有壁面的粗糙度下，顯然比單獨(dú)考慮某一部分的影響大，這也是A下降快的原因。對(duì)比單獨(dú)考慮葉片(C)和只不考慮葉片(B)的情況，發(fā)現(xiàn)后者的影響反而更大，對(duì)于本文，其原因是模型中的進(jìn)出水管道較長(zhǎng)，所占的水力損失的比例相對(duì)較大。對(duì)揚(yáng)程、效率進(jìn)行計(jì)算發(fā)現(xiàn)，壁面粗糙度從0.1 mm增大到0.75 mm時(shí)，A情況的計(jì)算揚(yáng)程從15 m下降到13.92 m，下降幅度7.2%；效率由83.9%下降到79.22%。C情況的計(jì)算揚(yáng)程從15.36 m下降到14.98 m，下降幅度2.5%；效率由86%下降到83.78%。

圖5和圖6為考慮泵所有部件粗糙度(A情況)時(shí)，葉片壓力面和吸力面的磨損速率分布圖，設(shè)置最大磨損率為2×10-6kg/(s·m2)，最小磨損率為1×10-8kg/(s·m2)，通過(guò)對(duì)比同一位置處的磨損速率來(lái)研究磨損的變化情況。圖5(a)和圖6(a)對(duì)應(yīng)葉片粗糙度0.1 mm，圖5(b)和圖6(b)對(duì)應(yīng)葉片粗糙度0.75 mm。對(duì)比圖5可以看出，隨著粗糙度的增大，磨損嚴(yán)重的葉片1(見(jiàn)圖5的標(biāo)示)處，磨損速率明顯降低。在磨損強(qiáng)度也比較大的葉片進(jìn)口處，磨損狀況基本沒(méi)有變化。從壓力面葉片整體來(lái)看，粗糙度增大時(shí)，葉片產(chǎn)生輕度磨損的面積變大。對(duì)比圖6可以看出，隨著粗糙度的增大，葉片吸力面在進(jìn)口處的磨損有輕度的加重，磨損強(qiáng)度較大的面積有輕微地增大。從整體來(lái)看，受到輕度磨損的區(qū)域面積增大。

圖5 壓力面磨損速率分布圖

圖6 吸力面磨損速率分布圖

圖7為葉輪在z=0.04 m處截面的流場(chǎng)圖，可以看出，粗糙度增大，水流速度有輕度的增加。流場(chǎng)的分布狀況沒(méi)有明顯的變化。圖8為葉片1的壓力面對(duì)應(yīng)的顆粒堆積速率圖，圖9為葉片3的吸力面對(duì)應(yīng)的顆粒堆積速率圖，顆粒堆積速率范圍為0～40 kg/(s·m2)。結(jié)合磨損速率圖可以發(fā)現(xiàn)，顆粒堆積速率大的位置處，磨損速率也較大。粗糙度增大時(shí)，葉片1壓力面出口處的顆粒堆積速率減小，葉片磨損得到改善；葉片3吸力面進(jìn)口處的顆粒堆積速率增大，葉片磨損有輕度的加重。因此，在本文所研究的顆粒粒徑及粗糙度范圍內(nèi)，顆粒堆積速率對(duì)磨損的影響很大。

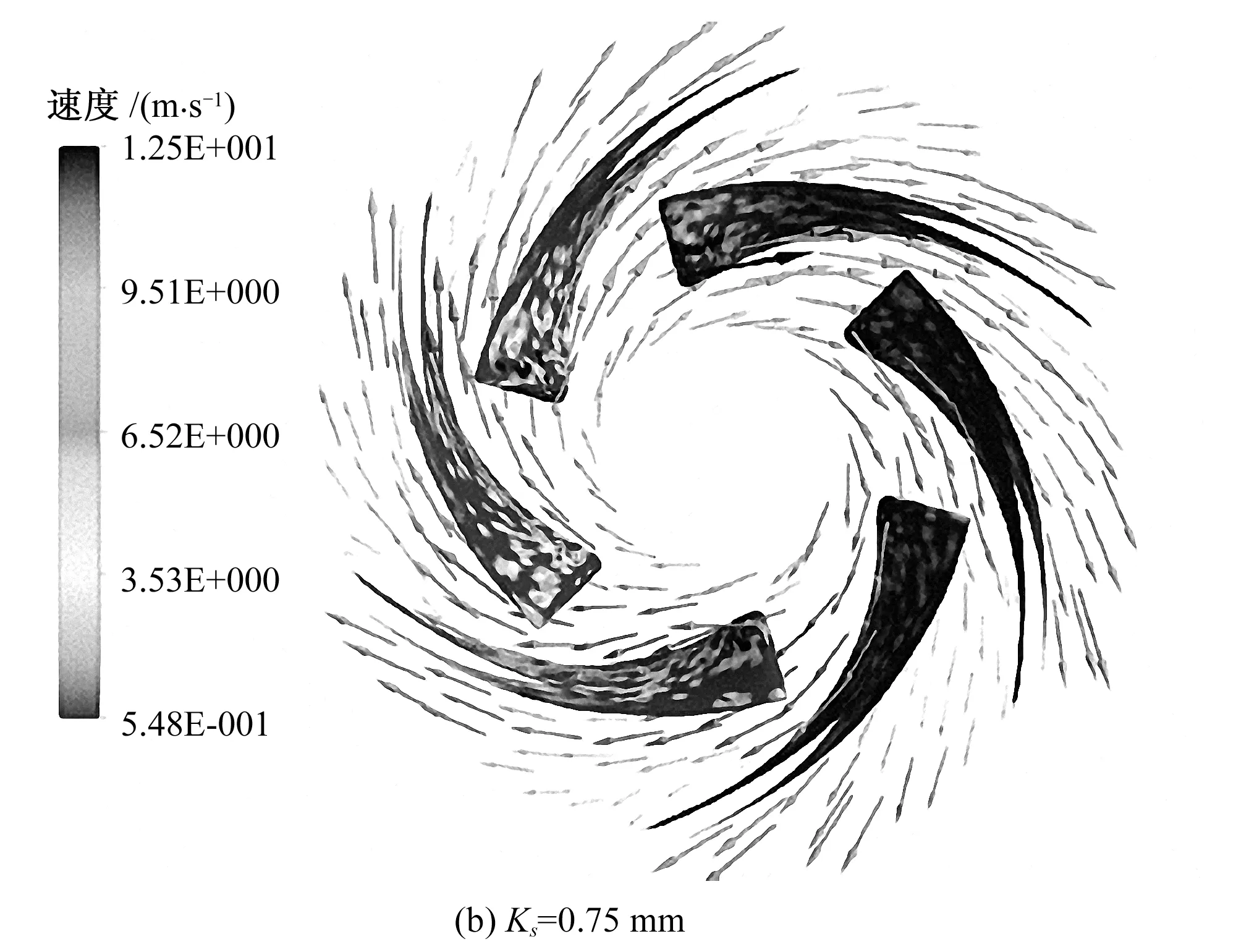
圖7 葉輪截面流場(chǎng)圖

圖8 壓力面葉片1處顆粒堆積速率圖

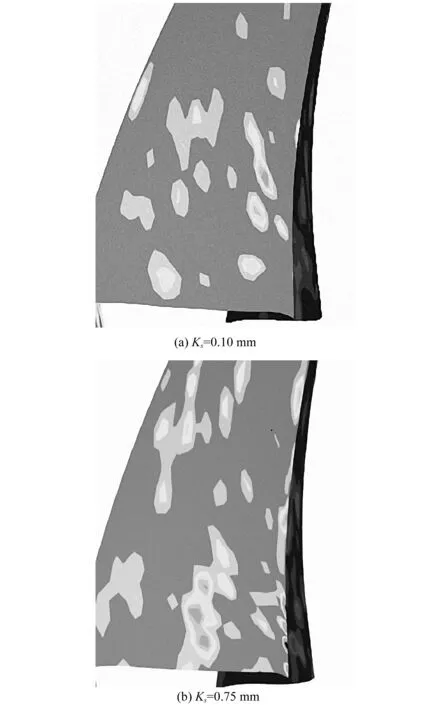
圖9 吸力面葉片3處顆粒堆積速率圖

5 結(jié) 語(yǔ)

采用歐拉-拉格朗日多相流模型，模擬了不同粗糙度時(shí)雙吸式離心泵內(nèi)的水流及泥沙顆粒運(yùn)動(dòng)，分析了粗糙度對(duì)水泵水力性能及葉片磨損狀況的影響，分析結(jié)果表明：粗糙度在研究的范圍內(nèi)增大時(shí)，葉片壓力面集中磨損的情況得到改善，吸力面進(jìn)口處的磨損稍有加重。壓力面集中磨損的區(qū)域變小，但壓力面及吸力面受到磨損的區(qū)域增加。

□

[1] 鄭槐卿. 離心泵葉輪流道表面粗糙度對(duì)效率的影響[J]. 水泵技術(shù)，1989，(1):9-13.

[2] 談明高，劉厚林，吳賢芳，等. 粗糙度對(duì)離心泵性能數(shù)值預(yù)測(cè)的影響[J]. 中國(guó)農(nóng)村水利水電，2011，(2):131-134.

[3] 李 龍，王 澤. 粗糙度對(duì)軸流泵性能影響的數(shù)值模擬研究[J]. 農(nóng)業(yè)工程學(xué)報(bào)，2004，(1):132-135.

[4] 錢忠東，王 焱，郜元勇. 雙吸式離心泵葉輪泥沙磨損數(shù)值模擬[J]. 水力發(fā)電學(xué)報(bào)，2012，(3):223-229.

[5] Wang Ze，Liu Wei-ming. Two modificatoryk-εturbulence models for turbulent swirling flows[J]. Journal of Hydrodynamics，2003，(2):51-57.

[6] Yakhot Victor Orszag Steven A. Renormalization group analysis of turbulence I. basic theory[J]. Journal of Scientific Computing，1986，(1):3-11.

[7] 李家星，趙振興. 水力學(xué)[M]. 南京:河海大學(xué)出版社，2001.