灌溉水資源安全閾值確定與高效配置

2016-03-26 07:31:39郭珊珊

中國農村水利水電 2016年8期

關鍵詞：模型

李茉，郭萍，郭珊珊

(中國農業大學中國農業水問題研究中心，北京 100083)

水資源的合理利用在農業生產中發揮關鍵的作用[1]。農業是我國用水大戶，用水比例達63.5%[2]。社會經濟的快速發展使工業、生活和生態用水與農業用水競爭激烈，導致灌溉用水供需矛盾日益突出，且我國灌溉用水管理不當，效率低。如何在考慮區域社會經濟和生態可持續發展的前提下合理且高效的配置灌溉水資源，成為區域水資源決策者面臨的緊迫任務。

國內外關于灌溉水資源優化配置已有大量研究，其中普通線性規劃模型由于計算簡便被廣泛應用[3]。針對我國灌溉用水效率低的特點，優化配置有限的灌溉水資源以提高區域灌溉水生產率比單純提高產量或產值更有實際意義，特別是在干旱和半干旱地區。因此，基于分式線性規劃的灌溉水資源優化配置可被采用[4,5]。考慮可持續發展的灌溉水資源優化配置需建立在灌溉用水安全閾值的基礎上。水資源安全閾值的研究主要是確定區域水資源系統安全區間的上下限值[6]，在此區間內，水資源處于安全狀態，社會經濟與生態可持續發展。對于水資源緊缺的干旱半干旱地區，尋找水資源安全閾值的下限值即不發生干旱的最小用水指標顯得尤為重要[7]。近些年，國內關于水資源安全閾值的研究成為熱點[7-9]，但多數集中于區域尺度上的研究，對側重考慮灌溉用水安全閾值的研究較少，尤其是基于灌溉用水安全閾值的灌溉水資源高效配置的研究鮮有報道。

本文以黑河中游的甘州區、臨澤縣、高臺縣為研究區域，首先采用模糊識別模型計算區域灌溉水資源與社會經濟生態協調發展的協調度，并以此協調度作為狀態變量，與由因子分析法確定的控制變量一起擬合基于突變理論的尖點突變模型，并以此確定灌溉水資源安全閾值。在此基礎上，構建灌溉用水高效配置優化模型并求解，得到的優化配水方案對研究區域水資源管理具有實際指導意義。

1 可變模糊識別模型與熵值法

可變模糊識別模型理論與方法是建立在相對隸屬度與相對隸屬函數概念的基礎上的。該方法可以反映水資源系統的復雜性、不確定性、一定時段內具有的動態性等特點，并且能夠客觀分析水資源與社會經濟生態協調發展的狀況。可變模糊識別模型可表示為[10]：

(1)

式中：vj為方案集綜合相對優屬度；i=1,2,…,I為指標種類；J=1,2,…,J為時段數；uij為指標i時段j的因子值；ωi為指標i的權重；μij(uij)為指標i時段j的相對隸屬度；α為優化準則參數，常取α=1(最小一乘方準則)和α=2最小二乘方準則)；p為距離參數，常取p=1(海明距離)和p=2(歐氏距離)。

令dbj={∑Ii=1[ωi(1-μij(uij)]p}1/p表示時段j的最優距離，dwj={∑Ii=1[ωiμij(uij)]p}1/p表示時段j的最劣距離，公式(1)中不同α和p取值的隨機組合可形成以下4種模型：①當α=1,p=1時，vj=∑Ii=1ωiμij(uij)，相當于模糊綜合評判模型；②當α=1,p=2時，vj=dwj/(dbj+dwj)，相當于理想點模型；③當α=2,p=1時，vj=1/{1+[(1-dwj)/dwj]2}，此時為sigmoid函數，是一個良好的閾值函數；④當α=2,p=2時，vj=1/[1+(dbj/dwj)2]，此時為模糊優選模型。

在上述各模糊識別模型中，一個重要的參數就是指標的權重ωi。關于指標權重的確定方法有很多，其中熵值法確定權重由于其客觀合理性在水資源評價領域中被廣泛應用[11]，其確定過程可總結如下：①歸一化非負處理評價因子集u′ij=[(uij-min(uij))/(max(uij)-min(uij))]+1，其中“+1”項為避免求熵時取對數的無意義；②計算指標i時段j占總體比例pij=u′ij/∑Jju′ij；③計算各因子權重ωi=di/∑Ii=1di，其中di=(1-ei)/(1-∑Ii=1ei)，ei=-[1/(ln(J)∑Jj=1pijln(pij))]。

選取代表灌溉水資源、經濟、社會及生態各維度的典型指標集合，記為B，在此基礎上，根據上述各可變模糊識別模型可以計算研究區域不同年份的灌溉水資源與社會經濟生態協調發展的協調度(以下簡稱“協調度”)。由于該“協調度”代表灌溉水資源的可持續利用狀態，在一定程度上反映灌溉水資源的安全程度，因此本文選用此“協調度”作為后述尖點突變模型的狀態變量。

2 尖點突變模型

突變理論是根據勢函數來研究對象的變化過程和突變線性，系統的勢函數可表示系統任一狀態值，這個值是控制變量與狀態變量的統一。水資源系統滿足尖點突變的兩個特性，突跳性和發散性，因此可采用尖點突變模型對水資源安全系統進行突變分析[7]。尖點突變模型由兩個控制變量和一個狀態變量構成，其勢函數可表示成：

V(x)=x4+qx2+rx

(2)

式中：x為狀態變量；q為主控制變量；r為次控制變量。

對勢函數求導可得到其臨界點，其表達式如下：

(3)

式(3)為尖點突變模型的平衡曲面，聯立式(2)和式(3)，得到分歧點方程為

8q3+27r2=0

(4)

令Δ=8q3+27r2代表突變判別式，當Δ>0時，系統是穩定安全的，當Δ<0時，系統會發生突變，當時是發生突變的臨界值。

實際應用中的具體步驟可表述如下：①選取勢函數中的控制變量和狀態變量。其中狀態變量為根據模糊識別模型求得的“協調度”，對于主控制變量和次控制變量的選擇，若指標集合B中指標較多，可先采用因子分析方法對指標進行篩選，根據旋轉后的因子負荷矩陣[12]排序選取主、次控制變量；②變量(包括控制變量和狀態變量)歸一化處理，其中“越大越優”指標采用公式u″ij=(u″ij-uijmin)/(uijmax-uijmin)計算，而“越小越優”指標采用公式u″ij=1-(u″ij-uijmin)/(uijmax-uijmin)計算；③熵值法計算各控制變量權重；④模型擬合，將尖點突變模型的平衡曲面寫成4x3=-2qx-r的形式，令y=4x3，則尖點突變平衡曲面擬合式可表述為y=k1(-2q′x′)+k2(-r′)+k3，其中q′，r′和x′分別為主控制變量、次控制變量和狀態變量的歸一化值，采用多元回歸分析法求得k1，k2，k3值；④根據擬合結果計算判別式Δ從而獲得灌溉用水安全閾值。

上述步驟中涉及用因子分析法對初始指標體系進行篩選得到主、次控制變量，其中因子分析法是從研究變量內部相關的依賴關系出發，把一些具有錯綜復雜關系的變量歸納為少數綜合因子的一種多變量統計方法[13]，計算步驟可歸納如下：①將原始指標體系標準化；②求標準化矩陣的相關矩陣；③求相關矩陣的特征值和特征向量；④計算各因子方差貢獻率和累計方差貢獻率；⑤根據方差累計貢獻率程度(不低于85%)確定公共因子；⑥通過正交旋轉法進行因子旋轉；⑦根據旋轉后因子負荷矩陣篩選主要影響因子。

3 灌溉水資源優化配置模型

以區域灌溉水生產率最大為目標函數，在有限水資源和灌溉用水安全閾值等約束下，對研究區域的地表水和地下水進行綜合配置。配水模型為線性分式規劃模型，分子為灌溉所獲得的產量，分子為區域分配的水量，分子分母同時優化，以期獲得區域最小灌水量下的最大產量。其數學表達式如下：

(5)

地表水可利用量約束：

(6)

地下水可利用量約束：

GWi≤Gi?i

(7)

灌溉用水安全閾值約束：

SWi+GWi≥Mi?i

(8)

非負約束：

SWi≥0,GWi≥0 ?i

(9)

式中：Z為目標函數，kg/m3；i為研究區域；SWi、GWi分別為區域i的地表配水量和地下配水量(決策變量)，m3；Yi為區域i的單方水產量，kg/m3；p為灌溉用水比例；以由各區域i組成的整體為閉合系統，Qu，Qs，Qd分別為河流上游來水，自產水與承諾的下泄水量，m3；Gi為區域i可開采的被農業利用的地下水量，m3；Mi為灌溉用水安全閾值下限，m3。

4 實例應用與結果分析

研究區域選定為黑河中游的甘州區、臨澤縣和高臺縣。黑河流域中游段即從鶯落峽至正義峽中間段，多年平均降雨125 mm，年均蒸發量1 200 mm，蒸發量遠大于降雨量，水資源短缺嚴重。中游農業用水占總用水量比例高達90%，灌溉水資源主要引黑河干流水和抽取地下水，還有少量小河流產水。根據國務院關于黑河分水目標，當鶯落峽多年平均來水為15.8億m3時，正義峽斷面的泄水量需達到9.5億m3，以保證黑河下游生態健康。中游灌溉可用水量因此被大量縮減，如何在保證中游灌溉用水安全的前提下高效的配置有限水資源，使得黑河中游段的水資源與社會經濟生態協調發展是水資源管理者需要考慮的問題。

根據多年統計與調研資料，獲得能夠代表三區(縣)灌溉水資源、經濟、社會和生態相關的典型指標體系如表1所示(以甘州區為例，各研究區域指標一致)。首先根據確定的指標體系計算三區(縣)的“協調度”，本文將四種可變模糊識別模型均做計算，最終取四種模型的平均值作為各研究區域的“協調度”，如圖1所示，其中由熵值法確定的三區(縣)各指標權重見表2，“協調度”的判斷標準為見表3。結合圖1和表3得到甘州區的水資源與社會經濟生態發展的協調程度在2000-2013年間呈好轉趨勢，其“協調度”從“明顯失調-動態平衡”狀態逐漸轉變成“動態平衡-基本協調”狀態，水資源基本呈可持續利用狀態。而臨澤縣和高臺縣的“協調度”整體呈下降趨勢，其中臨澤縣2000-2009年間的“協調度”呈波動狀態，2009-2012年間的“協調度”大幅度下降，2013年有所好轉，高臺縣2000-2002年間的“協調度”呈上升趨勢，之后保持三年平穩狀態，然后呈逐年下降趨勢。整體來講，臨澤縣和高臺縣水資源呈不可持續利用狀態，其原因可能是由于“分水”計劃導致中游水資源短缺嚴重，而甘州區作為張掖市的政治、經濟、文化中心，在有限的水資源情況下，優先保證甘州區的水資源可持續利用。將計算得到的三區(縣)4種模型“協調度”的歸一化平均值作為尖點突變模型的狀態變量。

表1 甘州區指標體系Tab.1 Index system of Ganzhou district

圖1 甘州區、臨澤縣和高臺縣的“協調度”Fig.1 Coordination degree of Ganzhou district, Linze County and Gaotai County

區域水資源指標用水總量/億m3灌溉定額/(m3·hm-2)灌溉水利用系數/%地下水量/億m3萬元GDP用水量/(m3·萬元-1)社會經濟指標GDP總量/億元人口/(m3·萬元-1)人均GDP/(萬元·人-1)糧食總產/億kg有效灌溉面積/萬hm2城鎮人均收入/(萬元·人-1)農民人均收入/(萬元·人-1)水費收入/萬元單方水產量/(kg·m-3)糧食單位面積產量/(kg·hm-2)生態指標年降雨量/mm林草灌溉面積/萬hm2甘州區0．060．050．050．040．07950．060．040．060．060．110．0550．0630．0550．070．070．040．03臨澤縣0．040．040．040．050．06670．070．070．050．060．140．0650．0690．0560．0520．070．040．03高臺縣0．050．040．070．050．04610．050．060．060．070．080．0530．0550．0710．0340．050．050．12

表3 “協調度”的判斷標準Tab.3 Criteria of coordination degree

各區(縣)指標體系均包含17個指標，指標相對較多，本文通過因子分析方法對各區(縣)指標進行篩選，根據旋轉后的因子負荷矩陣篩選主、次控制變量。表4為三區(縣)旋轉后因子負荷矩陣，根據各區(縣)各因子所占負荷值并協調各綜合因子，同時考慮與灌溉用水密切相關的指標，最終確定甘州區的主控制指標為用水總量、年降雨量、灌溉定額，次控制指標為農民人均純收入、糧食單方水產量、水費收入；臨澤縣的主控制指標為用水總量、灌溉水利用系數，次控制指標為萬元GDP用水量、有效灌溉面積、林草灌溉面積；高臺縣的主控制指標為用水總量、灌溉水利用系數、年降雨量，次控制指標為萬元GDP用水量、GDP總量、單方水產量。對選好的控制變量進行歸一化處理，并根據熵值法對選好的指標進行權重計算，擬合尖點突變模型，并擬合判別式與灌溉毛用水量之間的函數關系，如圖2所示。由于黑河中游處于水資源短缺地區，因此尋找的灌溉用水安全閾值為對應的下限值，即不發生干旱災害的最小灌溉用水量。從圖2中可以看出，甘州區和高臺縣歷年灌溉用水情況安全，只有個別年份判別式小于零，而臨澤縣的灌溉用水因其歷年判別式均小于零呈現不安全狀態，臨澤縣的灌溉用水在很大程度上不能滿足需求，極易發生干旱。根據圖2擬合的結果，可以得到甘州區、臨澤縣和高臺縣判別式與毛灌溉水量之間的函數關系分別為Δ甘=49x2-754.76x+2 901.4，Δ臨=-6.29x2+77.93x-247.35，Δ高=276.69x2-2 563.2x+5 941.4。通過對判別式求極值得到甘州區、臨澤縣和高臺縣的毛用水安全閾值分別為7.70，6.20和4.63億m3。根據三區(縣)多年渠系水利用系數平均值(甘州區：68.79%，臨澤縣：63.23%，高臺縣60.80%)和三區(縣)灌溉用水比例，得到甘州區、臨澤縣和高臺縣的凈灌溉用水安全閾值(Mi)分別為4.88，3.02和2.69億m3。

將得到的凈灌溉用水安全閾值輸入到高效配水優化模型中并對模型進行求解得到三區(縣)地表水和地下水優化配水方案。地表總可利用水量為：鶯落峽徑流(Qu=15.8億m3)+境內河流產流(梨園河2.37億m3+其他小河流1億m3，即Qs= 3.37億m3)-下泄到正義峽的水量(Qd= 9.5億m3)。甘州區、臨澤縣和高臺縣的地下水可開采量(Gi)分別為2.01，1.3和1.5億m3。甘州區、臨澤縣和高臺縣的單方水產量(Yi)分別為1.60，1.79和1.23 kg/m3。模型優化結果見圖3。優化的灌溉水生產率為1.58 kg/m3，比多年平均情況增長1.3%；優化的總灌水量為10.28 m3，比多年平均情況降低3%。優化的結果在保證三區(縣)灌溉用水安全的情況下，節約了水資源，并使灌溉水生產率有小幅度提高。從優化結果中可以得到，分配給三區(縣)的總地下水達到4.7億m3，雖然在總地下水可開采能力(4.81 m3)范圍內，但地下水用量比多年平均多了1.32億m3。由于配水是在滿足下泄到正義峽水量達到9.5億m3和灌溉用水安全閾值的基礎上的，此時地表徑流全部利用，若使地下用水量維持多年平均水平，則會導致下泄到正義峽的水量相應減少或不能完全滿足灌溉用水安全閾值要求，決策者可根據實際情況與需求對配水方案進行相應調整。

5 結語

(1)利用模糊可變識別模型計算甘州區、臨澤縣和高臺縣水資源與社會經濟生態協調發展的協調度，其中甘州區的“協調度”呈上升趨勢，臨澤縣和高臺縣的“協調度”呈下降趨勢。

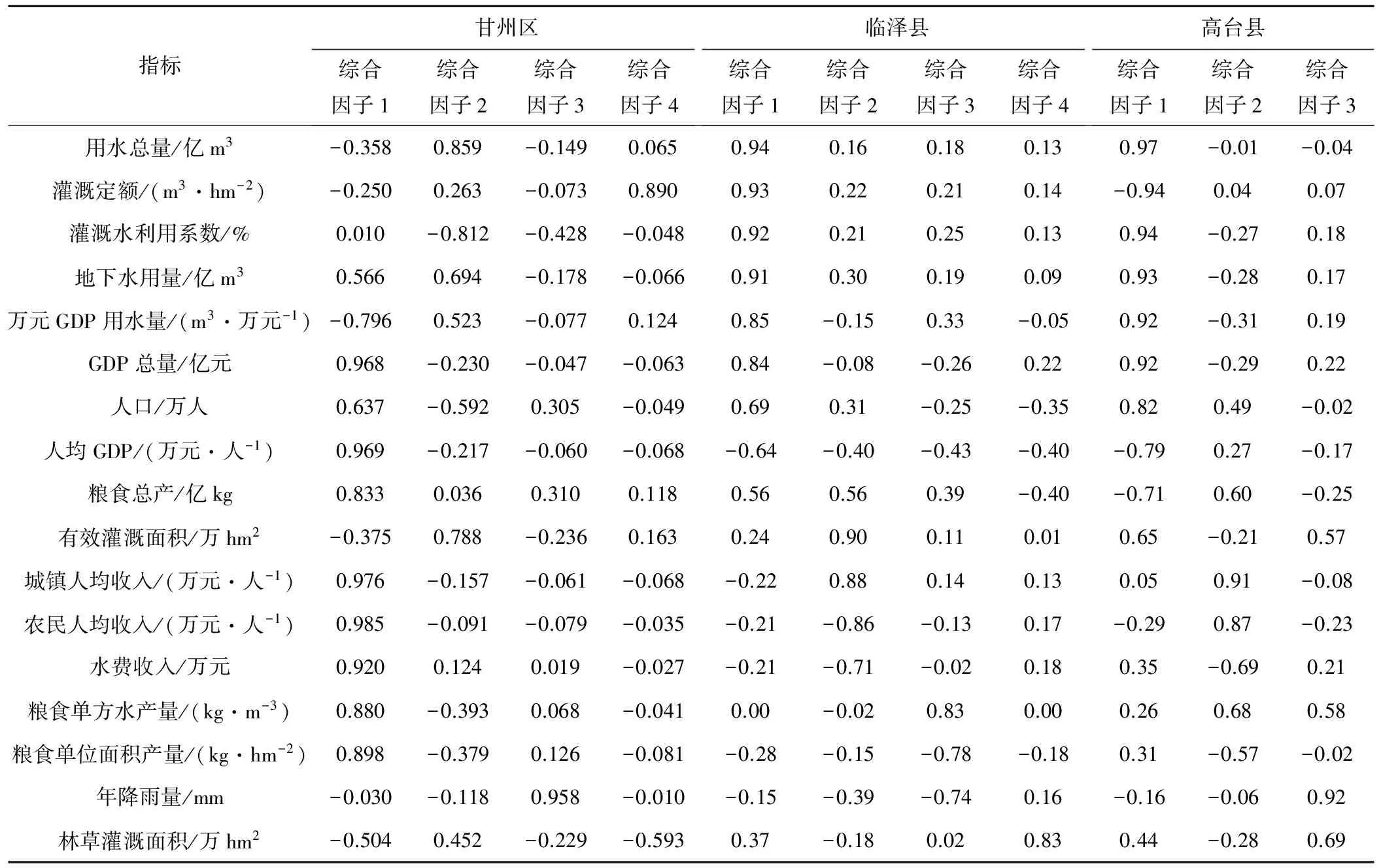
表4 因子分析旋轉后因子負荷矩陣Tab.4 The rotating factor loading matrix of factor analysis method

圖2 甘州區、臨澤縣和高臺縣的判別式值與用水量擬合Fig.2 Fitting results of the discriminant and irrigation water use of the three study areas

圖3 三區(縣)的優化配水結果Fig.3 Optimal water allocation of the three study areas

(2)以四種模糊可變識別模型計算的“協調度”均值作為狀態變量，結合利用因子分析法篩選出的主、次控制變量擬合尖點突變模型，根據判別式確定甘州區、臨澤縣和高臺縣的灌溉用水安全閾值下限分別為4.88，3.02和2.69億m3。

(3)以灌溉用水安全閾值為約束條件，以最大化灌溉水生產率為目標函數，構建灌溉水資源優化配置模型，優化得到灌溉水生產率為1.58 kg/m3，比多年平均增長1.3%；優化的總灌水量為10.28 m3，比多年平均降低3%。

□

[1] 張展羽, 司涵, 馮寶平, 等. 缺水灌區農業水土資源優化配置模型[J]. 水利學報, 2014,45(4):403-409.

[2] 中華人民共和國水利部. 中國水資源公報[R]. 2014.

[3] Singh A. Irrigation planning and management through optimization modelling [J]. Water Resources Management, 2014,28(1):1-14.

[4] Li M, Guo P, Singh V P, et al. An efficient irrigation water allocation model under uncertainty [J]. Agricultural Systems, 2016, 144:46-57.

[5] Guo P, Chen X H, Li M, et al. Fuzzy chance-constrained linear fractional programming approach for optimal water allocation [J]. Stochastic Environmental Research and Risk Assessment, 2014,28:1 601-1 612.

[6] 王靄景. 天津市水資源優化配置及安全閾值研究[D]. 北京：華北電力大學，2013.

[7] 張玉山, 李繼清, 梅艷艷, 等. 基于突變理論的天津市水資源安全閾值分析模型[J]. 遼寧工程技術大學學報(自然科學版), 2013,32(4):562-567.

[8] 暢明琦. 水資源安全理論與方法研究[D]. 西安：西安理工大學, 2006.

[9] 秦長海, 甘泓, 汪林, 等. 海河流域水資源開發利用閾值研究[J]. 水科學進展, 2013,24(2):220-227.

[10] 蓋美, 李偉紅. 基于可變模糊識別模型的大連市水資源與社會經濟協調發展[J]. 資源科學, 2008,30(8):1 141-1 145.

[11] 羅軍剛, 解建倉, 阮本清. 基于熵權的水資源短缺風險模糊綜合評價模型及應用[J]. 水利學報, 2008,39(9):1 092-1 104.

[12] 劉迅, 耿進強, 畢遠志. 基于因子分析法的水利工程標段劃分影響因素研究[J]. 中國農村水利水電, 2014,(12):91-95.