廣義ZK-MEW方程的行波解分支

?

廣義ZK-MEW方程的行波解分支

引文格式： 肖軍均，馮大河，孟霞.廣義ZK-MEW方程的行波解分支[J].桂林電子科技大學學報，2016,36(1):66-70.

肖軍均，馮大河，孟霞

(桂林電子科技大學 數學與計算科學學院，廣西 桂林541004)

摘要：為研究廣義ZK-MEW方程的動力學行為及有界行波解，運用動力系統分支理論，得到了該方程在給定參數條件下的相圖分支及光滑孤立波解、周期波解的解析表達式，并給出了這些解的數值模擬。

關鍵詞：廣義ZK-MEW方程；動力系統分支理論；光滑孤立波解；周期波解

基于ZK(Zakharov-Kuznetsov)方程[1]

和MEW(modified equal-width)方程[2]

文獻[3-5]研究了廣義ZK-MEW(Zakharov-Kuznetsov modified equal-width)方程：

(1)

其中：n∈Ν*，a、b、c為非零實常數。通過利用擬設孤立波方法研究方程(1)，Biswas[3-4]獲得了一些1-孤立子解、拓撲及非拓撲孤立波解。Pandir[5]運用擴展的實驗方程法，得到了方程(1)的孤立波解、有理和橢圓函數可積解。對方程(1)的動力學行為至今尚未研究，為此，利用動力系統分支理論[6-7]分析該方程的動力學行為并給出更豐富的精確行波解。

對方程(1)作行波變換：

可得常微分方程：

(2)

其中φ′=dφ/dξ。將方程(2)關于ξ積分一次，并且取積分常數為0，有

(3)

令φ′=y，可知方程(3)等價于如下Hamilton系統：

(4)

其中：A=-a/(bl+ck2)≠0；B=l/(bl+ck2)。顯然，系統(4)具有如下首次積分：

(5)

1系統(4)的相圖分支

設f(φ)=Aφn-Bφ，則有以下情況存在：

1)當n=1時，f(φ)僅有1個零點φ0=0，即系統(4)僅有1個平衡點O(0,0)。由于該情況比較簡單，僅考慮以下2種情況。

2)當n=2m，m∈N*時，f(φ)有2個零點：φ0=0，φ1=(A-1B)(n-1)-1，即系統(4)在φ軸上有2個平衡點：O(0,0)，P1(φ1,0)。

3)當n=2m+1時，f(φ)有3個零點：φ0=0，φ1=(A-1B)(n-1)-1，φ2=-φ1，即系統(4)在φ軸上有3個平衡點：O(0,0)，P1(φ1,0)，P2(φ2,0)。

令hi=H(φi,0),i=0,1,2，則

若Pe(φe,ye)為系統(4)的平衡點，則對應系統(4)的Jacobi矩陣為：

故有

由動力系統知識可知，若J(φe,ye)<0，則平衡點Pe為鞍點；若J(φe,ye)>0，則平衡點Pe為中心點；若J(φe,ye)=0，且Pe的龐加萊指數為0，則平衡點Pe為尖點。因此有如下結論成立：

1)當n=2m時：若B>0或B<0，則系統(4)有2個平衡點，且O為中心點或鞍點，P1為鞍點或中心點；若B=0，則系統(4)僅有1個平衡點O，且O為尖點。

2)當n=2m+1時：若AB>0，則系統(4)有3個平衡點，當B>0或B<0時，O為中心點或鞍點，P1、P2均為鞍點或中心點；若AB<0，則系統(4)有且僅有1個平衡點，當B>0或B<0時，O為中心點或鞍點；若B=0，則系統(4)僅有1個平衡點O，且O為尖點。

根據以上結論，可得系統(4)的相圖如圖1、圖2所示。

圖1　當n=2m時，系統(4)的相圖Fig.1　The phase portraits of system (4) for n=2m

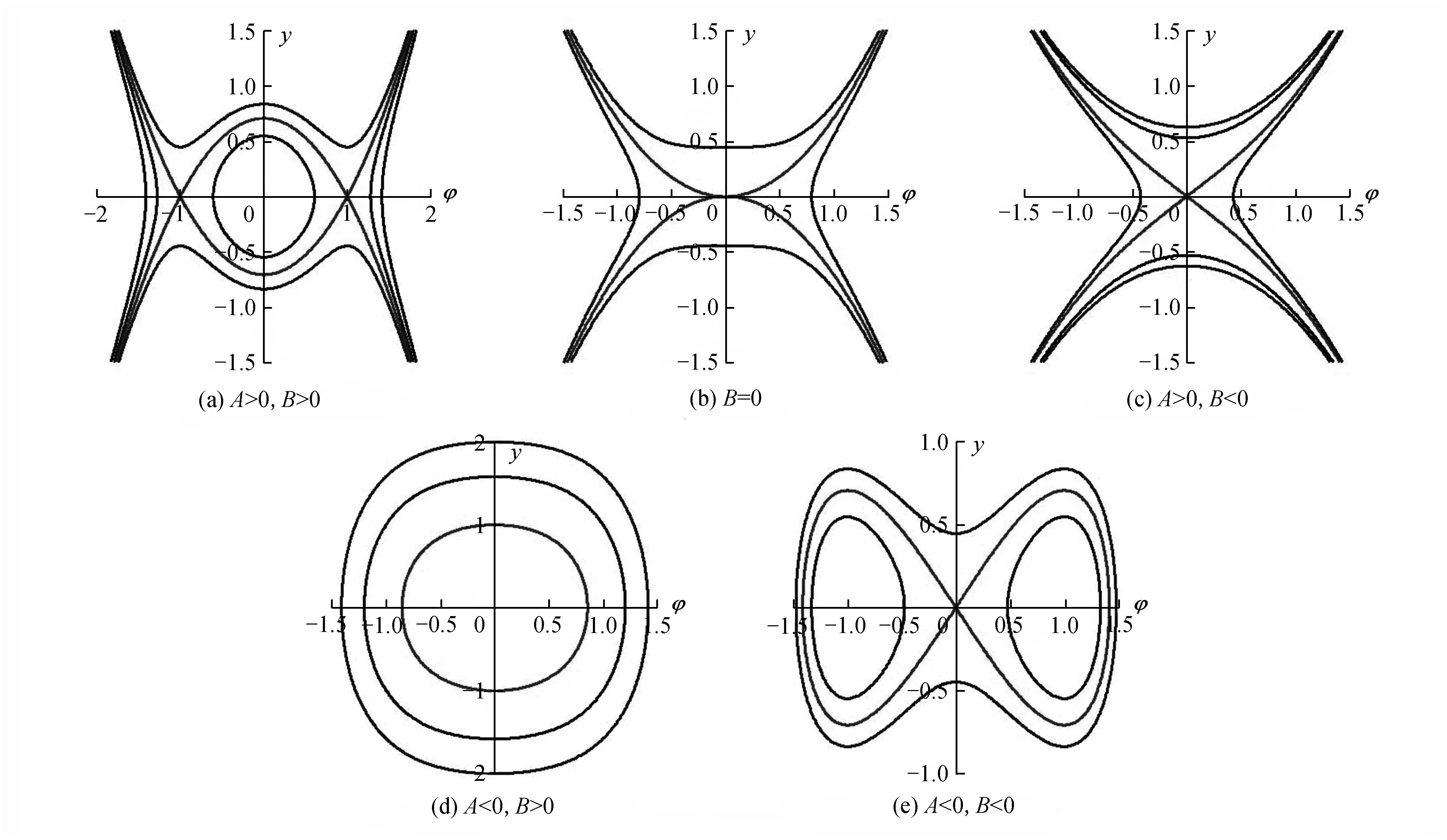
圖2　當n=2m+1時，系統(4)的相圖Fig.2　The phase portraits of system (4) for n=2m+1

2廣義ZK-MEW方程的行波解

定理1當n=2m，B>0時(見圖1(a)、(d))，對應系統(4)連接鞍點P1的同宿軌道H(φ,y)=h1，方程(1)有一個光滑孤立波解。對應系統(4)的周期軌道H(φ,y)=h∈(0,h1)，方程(1)有一族周期波解。

定理2當n=2m，B<0時(見圖1(b)、(f))，對應系統(4)連接鞍點O的同宿軌道H(φ,y)=0，方程(1)有1個光滑孤立波解。對應系統(4)的周期軌道H(φ,y)=h∈(h1,0)，方程(1)有一族周期波解。

定理3當n=2m+1，A>0，B>0時(見圖2(a))，對應系統(4)連接鞍點P1、P2的異宿軌道H(φ,y)=h1，方程(1)有1個扭(反扭)波解。對應系統(4)的周期軌道H(φ,y)=h∈(0,h1)，方程(1)有一族周期波解。

定理4當n=2m+1，A<0，B>0時(見圖2(d))，對應系統(4)的周期軌道H(φ,y)=h∈(0,+)，方程(1)有一族周期波解。

定理5當n=2m+1，A<0，B<0時(見圖2(e))，對應系統(4)連接鞍點O的同宿軌道H(φ,y)=0，方程(1)有2個光滑孤立波解。對應系統(4)環繞平衡點O，P1、P2的大范圍周期軌道H(φ,y)=h∈(0,+)，方程(1)有一族周期波解。對應系統(4)分別環繞中心點P1、P2的2族周期軌道H(φ,y)=h∈(h1,0)，方程(1)有2族周期波解。

結合相圖分析方法及定理1~5，考慮方程(1)在n=2時的行波解。

2.1n=2，A>0，B>0(圖1(a))

1)對應系統(4)連接鞍點P1(B/A,0)的同宿軌道H(φ,y)=h1=B3/6A2，方程(1)有1個光滑孤立波解。式(5)可改寫為：

(6)

由系統(4)的第1個方程和方程(6)可得：

(7)

取初值φ(0)=-B/2A，對方程(7)積分一次，可得方程(1)的1個谷形光滑孤立波解(也稱暗孤立子)的顯性表達式：

(8)

2)對應系統(4)環繞中心點O(0,0)的周期軌道H(φ,y)=h∈(0,h1)，方程(1)有一族周期波解。式(5)可改寫為：

(9)

其中ψi(i=1,2,3)為方程(2A/3)φ3-Bφ2+2h=0的3個實根，且ψ1>ψ2>φ>ψ3。由系統(4)的第1個方程和式(9)可得：

(10)

取初值φ(0)=ψ3，對方程(10)兩端積分一次，可得方程(1)周期波解的顯性表達式：

(11)

圖3　周期波解(11)趨近于谷形光滑孤立波解(8)的波形變化Fig.3　The waveform changes for periodic wave solutions (11) tending to smooth solitary wave solutions with valley type (8)

1)對應系統(4)連接鞍點O(0,0)的同宿軌道H(φ,y)=0，方程(1)有1個光滑孤立波解。因此，方程(5)可改寫為：

(12)

聯立方程(12)和系統(4)的第1個方程，可得

(13)

取初值φ(0)=3B/2A，并對方程(13)積分一次，可得方程(1)的1個峰形光滑孤立波解(也稱亮孤立子)的顯性表達式：

(14)

2)對應系統(4)環繞中心點O(0,0)的周期軌道H(φ,y)=h∈(h1,0)，方程(1)有一族周期波解，其表達式與方程(11)相同。

2.3n=2，A<0，B>0(圖1(d))

1)對應系統(4)連接鞍點P1(B/A,0)的同宿軌道H(φ,y)=h1=B3/6A2，方程(1)有1個峰形光滑孤立波解，其顯性表達式為：

(15)

2)對應系統(4)環繞中心點P1(B/A,0)的周期軌道H(φ,y)=h∈(0,h1)，方程(1)有一族周期波解。因此，方程(5)可改寫為：

(16)

其中ψ1>φ>ψ2>ψ3。由系統(4)的第1個方程和方程(16)可得：

(17)

取初值φ(0)=ψ1，并對方程(17)積分一次，可得方程(1)的周期波解，其顯性表達式為：

(18)

其中：

2.4n=2，A<0，B<0(圖1(f))

1)對應系統(4)連接鞍點O(0,0)的同宿軌道H(φ,y)=0，方程(1)有1個峰形光滑孤立波解，其顯性表達式為：

(19)

2)對應系統(4)環繞中心點P1(B/A,0)的周期軌道H(φ,y)=h∈(h1,0)，方程(1)有一族周期波解，其表達式與方程(18)相同。

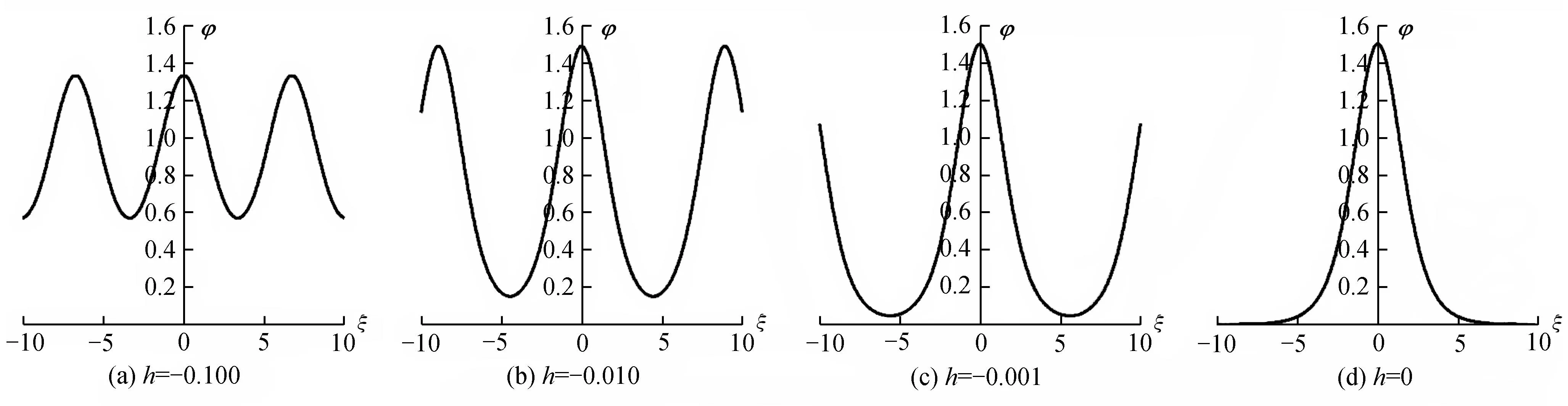
圖4　周期波解(11)趨近于峰形光滑孤立波解(19)的波形變化Fig.4　The waveform changes for periodic wave solutions (11) tending to smooth solitary wave solutions with peak type (19)

利用動力系統分支理論和微分方程定性分析方法，研究了廣義ZK-MEW方程，獲得了該方程所有參數分支和光滑孤立波解、扭(反扭)波解、周期波解存在的條件，進而給出了當n=2時的所有精確行波解的顯性表達式。通過對行波解的分析及數值模擬可知，隨著h的變化，周期波解逐漸趨近于光滑孤立波解。

參考文獻:

[1]INFELD E.Self-focusing of nonlinear ion-acoustic waves and solitons in magnetized plasmas[J].Journal of Plasma Physics,1985,33(2):171-182.

[2]WAZWAZ A.The tanh and the sine-cosine methods for a reliable treatment of the modified equal width equation and its variants[J].Communications in Nonlinear Science and Numerical Simulation,2006,11(2):148-160.

[3]BISWAS A.1-soliton solution of the generalized Zakharov-Kuznetsov modified equal width equation[J].Applied Mathematics Letters,2009,22(11):1775-1777.

[4]BISWAS A.Topological and non-topological solitons for the generalized Zakharov-Kuznetsov modified equal width equation[J].International Journal of Theoretical Physics,2009,48(9):2698-2703.

[5]PANDIR Y.New exact solutions of the generalized Zakharov-Kuznetsov modified equal-width equation[J].Pramana-Journal of Physics,2014,82(6):949-964.

[6]LI Jibin,LIU Zhengrong.Smooth and non-smooth travelling waves in a nonlinearly dispersive equation[J].Applied Mathematical Modelling,2000,25(1):41-56.

[7]FENG Dahe,LI Jibin.Bifurcation methods of dynamical systems for handling nonlinear wave equations[J].Pramana-Journal of Physics,2007,68(5):863-868.

[8]BYRD P F,FRIDMAN M D.Handbook of Elliptic Integrals for Engineers and Scientists[M].Berlin:Springer,1971:72-79.

編輯：張所濱

Bifurcations of traveling wave solutions for generalized ZK-MEW equation

XIAO Junjun, FENG Dahe, MENG Xia

(School of Mathematics and Computational Science, Guilin University of Electronic Technology, Guilin 541004, China)

Abstract：To study the dynamical behaviors and bounded traveling wave solutions of generalized ZK-MEW equation, the bifurcations of phase portraits and the representations of smooth solitary wave solutions and smooth periodic wave solutions are obtained under the given parametric conditions by employing the bifurcation theory of dynamic system. Moreover, the numerical simulations for those solutions are provided.

Key words：generalized ZK-MEW equation; bifurcation theory of dynamic system; smooth solitary wave solutions; periodic wave solutions

中圖分類號：O175.1

文獻標志碼：A

文章編號：1673-808X(2016)01-0066-05

通信作者：馮大河(1970-)，男，湖南懷化人，教授，博士，研究方向為動力系統的分支與混沌、微分方程定性理論。E-mail：dahefeng@hotmail.com

基金項目：國家自然科學基金(11162004,11461021)；桂林電子科技大學研究生教育創新計劃(YJCXS201557)

收稿日期：2015-10-09