基于FPGA平衡小車的設計

天津理工大學 王孟軒 陳子娟 汪 煊 李秀順

基于FPGA平衡小車的設計

天津理工大學 王孟軒 陳子娟 汪 煊 李秀順

隨著科技進步，生活水平的提高，人們追求智能與舒適的愿望也日益強烈。從而催生了許多智能化的產品。如智能電視、智能小車等。如何實現小車的自動快捷駕駛，也成為人們心中的向往與疑問，基于這種趨勢與需求，著眼于實際情況。本文介紹了基于MPU6050的自平衡小車系統的設計。系統基于陀螺儀等傳感器采集姿態信息，通過對比分析一階互補濾波和卡爾曼濾波的優缺點，采用卡爾曼濾波算法，并利用PID平衡算法，對小車的速度傾斜角度平衡狀態來進行檢測，并通過FPGA來控制電機來實現雙輪小車自如平衡地運動。從而實現小車智能自主控制的目的。本設計獲得了2016年“京微雅格杯FPGA應用大賽”一等獎。

FPGA；平衡車；PID算法；卡爾曼濾波

1 設計原理

1.1 產品調研

目前，電動平衡車主控芯片大多數是使用ST的一款32單片機——STM32F103系列，單片機由于是單線程，程序語句需要等待單片機周期才能執行。因此基于單片機設計的程序運行速度較慢，而FPGA由于是硬件電路，運行速度直接取決于晶振速度，速度較快且系統穩定。所以本設計擬采用基于FPGA的CME—M7系列芯片和TB6612FNG、HC-05、MPU6050完成雙輪電動車的設計。

1.2 原理示意圖

圖1 原理示意圖

1.3 設計原理

雙輪平衡車的控制思想是基于一級倒立擺的模型，當車體發生傾斜時，傳感器會檢測到車體角度的變化，控制系統根據車體角度的變化，控制電機向傾斜方向轉動，從而產生抵抗傾斜的力矩，使車身維持在平衡狀態。當車體不發生傾斜時，平衡車會在小范圍內實現動態平衡。所以，傾角越大加速度越快。在此策略下，平衡車能夠實現靜止、前進、后退等各種運動狀態，從而保證平衡車的穩定運行。小車作為一個控制對象，它的輸出量是兩個電機的轉動速度[1]。小車的運動控制任務可以分解成以下三個基本任務：

控制小車平衡：通過控制兩個電機正反向運動保持小車直立平衡狀態；

控制小車速度：通過調節小車的傾角來實現小車速度控制，實際上最后還是演變成通過控制電機的轉速來實現車輪速度的控制。

控制小車方向：通過控制兩個電機之間的轉動差速實現小車轉向控制。

小車直立和方向控制任務都是直接通過控制小車兩個電機完成的。在實際控制中，是將控制小車直立和方向的控制信號疊加在一起加載電機上，只要電機處于線性狀態就可以同時完成上面兩個任務。小車的速度是通過調節小車傾角來完成的。小車不同的傾角會引起小車的加減速的變化，從而達到對于速度的控制。

由上述原理分析可知，車身需要采集的主控芯片信息有車身加速度、車身角加速度、電機速度和位置信息等。因此本設計以陀螺儀和加速度計作為傳感器，采用FPGA作為主控芯片，通過電機驅動電路驅動直流電機實現電動雙輪玩具小車的姿態控制。控制器通過IIC串口通信協議讀取傳感器的姿態信息，經過濾波算法后進行數據的融合分析，得到小車的姿態，再通過姿態更新后，進入控制模塊，控制算法根據小車的姿態計算出驅動電機所需的PWM信號，電機控制部分主要算法采用PID算法，再通過雙閉環反饋控制（速度閉環控制和位置閉環控制），使小車穩定運行達到動態平衡。

2 設計流程

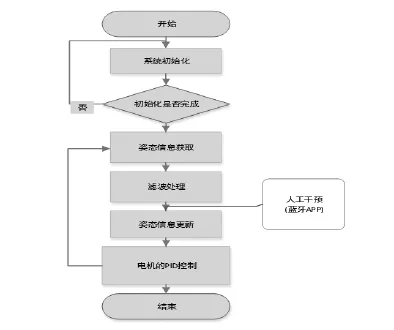
圖2 設計流程圖

2.1 姿態信息采集模塊

為實現小車的直立行走，需要利用MPU6050姿態傳感器和霍爾正交編碼器采集以下信息：

（1）小車傾角速度陀螺儀信號，獲得小車的傾角和角速度。（2）重力加速度信號（z軸信號），補償陀螺儀的漂移。

（3）小車電機轉速脈沖信號，獲得小車運動速度和位置信息，進行速度控制。

2.2 卡爾曼濾波器

兩輪自平衡小車系統具有多變量、非線性、強耦合、參數不確定等特性，是一個集動態決策和規劃、環境感知、行為控制和執行等多種功能于一體的綜合復雜系統.因此，采集小車的姿態信息很困難，所以我們必須增加濾波模塊以排除信號噪聲和動態加速度的干擾[2]。通常濾波分為一階濾波、互補濾波和卡爾曼濾波。

卡爾曼濾波（Kalman filtering）一種利用線性系統狀態方程，通過系統輸入輸出觀測數據，對系統狀態進行最優估計的算法。在本系統中，測量角度和測量角速度存在著導數關系，在這種情況下，我們不直接估計車體的角速度，而是采用加速度計的測量值來估算偏差gyro_bias , gyro_bias可以作為狀態向量的另一個元素。我們把車體的角度和角速度用入下關系時表示:

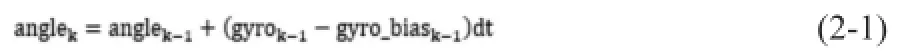
式中：anglek為估算的k時刻傾角；

anglek-1上一時刻加速計的測量值；

dt為采樣時間。

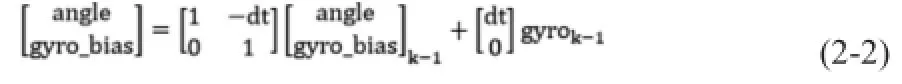
過程噪聲的協方差矩陣形式如下：

R=[R_angle]為觀測噪聲的協方差矩陣，且車體的角度與角速度中含有的噪聲為白噪聲加速度計測得的車體角度的過程噪聲的協方差為Q_ angle，陀螺儀測得的車體的角速度的過程噪聲協方差為Q-gyro。它們取不同的值代表了不一樣的信任程度。如果認為陀螺儀的可信度更高，可以把Q-gyro設置的小一些，如果認為加速度計的可信度更高可以把Q_ angle設置的小一些。R矩陣代表觀測噪聲的協方差，加入R很大，說明系統具有很大的噪聲。

仿真數據分析：

由式(2-1)我們可以編寫具體的卡爾曼濾波算法，并加以仿真。

在仿真過程中，通過調整協方差系數，可以控制濾波效果，仿真結果如圖3所示。通過圖3可以看出，加上噪音后，輸入卡爾曼濾波器的信號品質很差，通過卡爾曼濾波器濾波后，消除了輸出信號的噪聲，輸出信號可以很好地跟蹤理想信號。

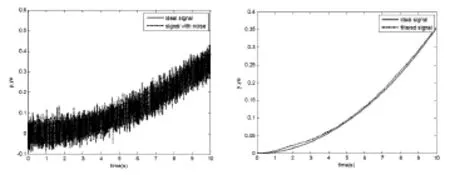
圖3 仿真結果圖

通過分析仿真及實測數據，可以看出，所設計的控制系統能夠很好地控制自平衡兩輪車直立，且自平衡車前后擺動較小，這證明了該控制器設計合理，控制器各參數選擇合適，硬件系統工作正常。

2.3 姿態信息更新

雙輪玩具小車是非線性、多階次、不穩定的系統，要實現其動態平衡，控制小車完成相應的動作，即給出相應的姿態信息，將控制信號重新寫入存儲器，由于其平衡狀態是處于動態，所以需要不斷的進行測量更新，針對兩輪自平衡車傾角的測量問題,采用了卡爾曼多傳感融合算法。該算法融合了加速度傳感器和陀螺儀傳感器數據,實現了兩輪自平衡車傾角實時在線估算，控制器給出控制信息后又控制系統驅動電機工作，采用了比例微分(PID)控制算法,實現了兩輪自平衡車姿態的穩定控制[3]。

2.4 電機驅動控制

2.4.1 雙輪平衡車控制特點

兩輪平衡車需要解決的問題是在前進、靜止、退過程中都要保持車體的平衡。它使一級倒立擺的運動方式變得更加靈活，更加多樣化。對于不完整非線性的系統，考慮下面介紹的PID控制方法:

PID控制是最常見的控制算法，它主要是對被控系統進行偏差調節。實現被控量的值與要求的值達到一致。但為了適應不同的過程，需要給出合理的控制規律，否則，PID控制器達不到預定效果。控制算法根據小車的姿態信息計算出PWM信號，再通過閉環反饋控制使小車完成相應的動作。根據角度角速度變化，控制電機來完成當前的平衡，以及在車體在運動過程中的各個姿態。

2.4.2 速度、位置雙閉環控制

我們一般在速度閉環控制系統里面，使用增量式PI控制，而在我們的微處理器里面，因為控制器是通過軟件實現其控制算法的，所以必須對模擬調節器進行離散化處理，這樣它只需根據采樣時刻的偏差值計算控制量。因此，我們需要使用離散的差分方程連續的差分方程。如下部分給出了小車的雙閉環控制原理

速度、位置雙環控制由以上兩個控制器進行嵌套而成因為雙閉環控制過程較復雜，故給出其控制原理圖4如下：

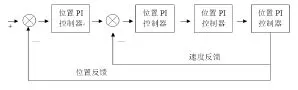
圖4 雙環控制原理圖

2.4.3 PWM輸出

要產生頻率和脈沖寬度可調的PWM波形，這可通過FPGA豐富的硬件資源和可以配置I/O引腳來實現。嵌入式系統中FPGA的應用設計關鍵是系統軟硬件功能的劃分。通過計數器的方式實現PWM的輸出。

2.4.4 電機PID控制算法的反饋系數的確定

由上文中PID控制的原理可知，比例環節輸出的控制信號與系統誤差e(t)成比例，比例系數越大，系統反應越靈敏，精度越高，但也會使調節震蕩更劇烈，甚至造成系統不穩定。積分環節輸出的控制信號與誤差的積分成比例，

積分系數大，可以更快地消除穩態誤差，但如果積分系數太大，則會產生較大的超調和長時間的波動。微分環節輸出的控制信號與誤差的變化率成比例，微分調節主要作用是對系統變化做出預警，產生提前的調節。微分控制可以使系統相位超前，抵消積分作用造成的相位滯后，同時可以減小超調，但微分系數過大，可能造成系統不穩定[4]。

根據這一原理，進行了大量的實驗調控，得到比較符合要求的實驗數據，再通過大數據的分析和計算確定反饋比例系數。由于本系統采用CME——M7，其具有ARM內核，可以做SOC，能將算法級的復雜程序直接放在ARM內核中，降低程序的開發難度。

3 最終成果展示

該設計采用PID控制算法對角度，角速度進行控制，使角速度可控，使系統反應時間大大縮短，電機驅動的PWM輸出，如圖5所示。實物小車展示表明小車確實可以平衡穩定的運行，當小車具有一定傾角的時候小車能保持平衡并能根據傾角完成相應的動作，以及展示小車抗干擾能力和對復雜路面的適應能力。

圖5 平衡小車實物展示

[1]楊世勇,徐麗萍,王培進.單級倒立擺的PID控制研究[J].控制工程,2007(B05):23-24.

[2]蔡述庭.“飛思卡爾”杯智能汽車競賽設計與實踐:基于S12XS和Kineris K10[M].北京:北京航空航天大學出版社,2012:248-251.

[3]張志強.基于STM32的雙輪平衡車[A].電子設計工程,2011:103-106.

[4]袁澤睿.兩輪自平衡機器人控制算法的研究 [D].哈爾濱 :哈爾濱工業大學,2006:22-31.

王孟軒（1993-），男，寧夏銀川人，現就讀于天津理工大學電子信息工程學院。