北京軌道交通系統結構與整體連通性分析

文_陳鍇（北京理工大學 機械與車輛學院，北京 100081）

北京軌道交通系統結構與整體連通性分析

文_陳鍇（北京理工大學 機械與車輛學院，北京 100081）

為定量分析軌道交通系統整體連通性受單個站點的影響提出方法。在Space-L拓撲結構中，從全局網絡效率計算入手，比較單一節點失效后全局網絡效率與原始全局網絡效率的變化情況，從而對各站點對整個系統連通性的影響進行評價。在分析比較各站點復雜網絡參數及相對位置后，得出結論：單個站點對整個系統連通性的影響主要與其在網絡中的相對位置有關；位于末端支路與環狀結構交匯處的站點對連通性影響最大，這些站點一旦失效，將可能導致整條線路崩潰。

交通規劃；軌道交通系統；復雜網絡；連通性；整體網絡效率

軌道交通線網的結構與性能一直是國內外研究的熱點。李海峰等將軌道交通的網絡分為放射形軌道交通網絡、“環+放射形”軌道交通網絡、方格形軌道交通網絡和遍布整個城市的軌道交通網絡等【1】。沈景炎提出，盡管每座城市線網的構架各有特點，但總體上可以歸納為由放射形線網、設置環線的線網和棋盤式等基本功能單元組合而成【2】。

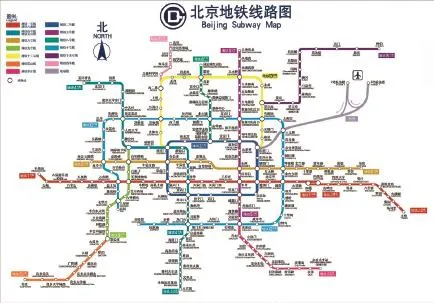
但現有的研究往往集中在城市中心區域的網絡結構，忽略了軌道交通線網末端對整體網絡連通性的影響。如圖1，北京市的軌道交通線網可以視為較為典型的“環+放射形”軌道交通網絡。截止至2016年5月，北京市軌道交通系統共有站點277座，其中位于四環外的站點共142座，占總數的51.3%；其中位于環狀結構外的末端支路站點111座，占總數的40.1%。

這些末端支路站點的存在使得軌道交通線網的功能更加完善，與此同時，由于居住與就業不匹配導致的早晚高峰大規模通勤使得部分線路負荷度過高，最高甚至達到144%。以地鐵5號線天通苑南站、天通苑站和天通苑北站為例。這些站點所在區域土地開發性質較為單一，以住宅為主，缺乏就業機會。因此在早晚高峰，形成了巨大的通勤交通，并呈現出明顯的潮汐交通流向【3】。因此早晚高峰這些站點內普遍存在擁擠和旅客滯留的情況。當擁擠和滯留達到一定程度時，節點功能失效，從而會對整個網絡的連通性產生負面影響。

本文通過搭建北京市軌道交通網絡模型，利用全局網絡效率分析了地鐵網絡末端結構對整體連通性的影響。

軌道交通系統與復雜網絡

復雜網絡及研究途徑

復雜網絡是具有眾多節點以及特定功能的特殊網絡結構，它擁有一定的幾何性質以及相應的統計規律。因此，統計物理和圖論都是研究這種共性的有效工具。

從圖論角度來講，網絡是指由一個點集和一個邊集組成的相互關聯的圖【6】，且中的每條邊都有的一對點與之對應。如果任意與對應同一條邊，則稱為無向網絡，否則為有向網絡；如果任意，則稱為無權網絡，否則為加權網絡。

從統計物理學的角度來看，復雜網絡可以視作一個包含大量相互作用個體的復雜系統。它將個體抽象為節點，將個體間的相互作用抽象為邊，通過研究網路的物理參數進而了解系統結構和運動方式。

軌道交通網絡的構建

基于北京市軌道交通系統的物理連接，以276個站點為節點（其中機場2號航站樓站、機場3號航站樓站視為一個站點），各站點間實際直接連通的地鐵線路為邊，采用Space-L法構建復雜網絡。構建結果如圖2。根據圖示，可以較為清晰地將站點劃分為環狀結構內部站點和環狀結構外的末端支路站點。

在構建過程中，遵循以下原則：

1. 任意直接連通節點可互為出發地和目的地，將整個網絡抽象為無向網絡；

2. 不考慮城市軌道交通中的各條線路的全天運用車組數、發車時間以及各線路發車間隔差異等因素，即不考慮網絡中連接權重問題，將整個網絡抽象為無權網絡；

3. 不考慮站間距差異，任意相鄰兩站間距視為相等；

4. 換乘站不重復計數。為方便相關參數計算，本文同時構建了鄰接矩陣表示該網絡結構。其中（1）

復雜網絡的基本統計特征

目前在文獻中出現的幾何量有：度分布、最短路徑、相關系數、聚類系數、邊密度、介數、平均度等等。它們分別描述復雜網絡不同方面的結構特點，可以比較全面的描述復雜網絡的內在特征。其中較為基本的統計特征有：度(degree distribution)、平均路徑長度(average pathlength)。

度與度分布

節點度是衡量節點在復雜網絡中重要性的指標，節點的度值表示與相鄰的節點數目。一般情況下，節點度值越高，該節點在網絡中的重要性越高。網絡上所有節點的平均值稱為網絡平均度，記為。

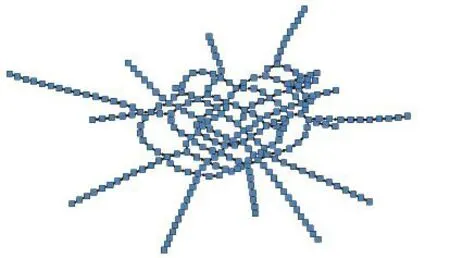
圖2 北京軌道交通系統拓撲圖

網絡中節點度的分布情況可以用分布函數進行表示。

根據定義統計得到北京市軌道交通系統276個站點的度值，平均度值為2.29。部分節點度值如表1：

表1 部分節點度值

整個網絡度分布結果如圖3：

圖3 網絡度分布

根據以上統計結果，我們可以看出，度值為2的節點占絕大多數。這是由于城市軌道交通線路的特殊性決定的，城市軌道交通網絡的延伸都是以線的形式增加的，除了始發站外，其他車站節點都是以度值2的形式增加的【7】。根據文獻[8]，目前與2010年相比，平均度值有較大程度的提高，這意味著北京市軌道交通系統網絡的環狀結構內的網絡密集度在逐漸增大，這與北京市軌道交通系統的實際情況基本相符。

平均路徑長度

平均路徑長度即網絡中任意兩點間最短距離的平均值，即：（2）

其中，表示網絡中節點個數，表示任意兩節點、間的距離。利用pajek軟件計算得北京市軌道交通系統平均最短路徑為14.39，較2010年有所下降。這體現了隨著網絡內部的不斷優化，換乘更加便捷。

網絡連通性評價

評價參數的選擇

在大多數文獻中，一般選用平均路徑長度作為評價網絡連通性的指標。其評價方法為網絡平均路徑越短，網絡連通性越好，反之則連通性越差。但針對軌道交通系統網絡，這種評價方法存在一定的問題。由于軌道交通網絡中往往存在較大比例的度值為1或2的節點，當部分節點被破壞，網絡中出現孤立點時，只能計算網絡中最大連通子圖平均路徑長度。此時平均最短路徑減小，這與連通性降低的事實相悖。

因此，這里我們引入網絡效率這一參數對網絡連通性進行評價。在無權網絡中，我們定義兩個節點之間的距離的倒數為兩個節點間的效率，即：（3）

當兩節點間不連通時，兩節點間路徑長度趨近于正無窮，則兩節點間效率為（4）

針對整個網絡，我們定義整個網絡中任意兩個節點間效率的平均值為全局網絡效率(Global Efficiency)即：（5）

類似的，針對局部網絡，我們定義局部網絡效率（Local Efficiency）為（6）

其中是節點的臨近組成的網絡。

此處引用Crucitti P.文中的圖例【4】，試比較兩種評價指標在網絡存在孤立點的情況下參數的不同，如下圖4所示：

圖4 Crucitti P.文中的圖例Fig.4 The legend of Crucitti P.

上兩圖中G1、G2，節點數目完全相同，僅邊數存在差異，G2中有孤立點，因而只能計算G2最大連通子圖的平均最短路徑長度。利用公式（2）計算，得到L1=1.3， L2=1。根據計算結果，G2連通性優于G1的結論與實際情況不符。利用公式（5）計算得，。所得結論與事實相符合。

因此利用網絡效率能夠更準確的反映城市軌道交通網絡連通可靠性。網絡全局效率反映了整個網絡的連通性強弱，網絡全局效率與網絡的連通可靠性呈正相關；當網絡中部分節點失效后，全局網絡效率降低。

網絡效率計算

本文為分析軌道交通網絡末端結構對網絡整體連通性的影響，逐一模擬了針對單一站點的攻擊，比較單一節點受到攻擊后，整體網絡效率的變化情況。主要工作通過MATLAB完成，核心代碼如下：

A=sparse(A);

ShortPath=graphallshortestpaths(A);

E=1./ShortPath;

E(E==inf)=0;

Eglob=(1/(length(A)*(length(A)-1)))*sum(sum(E))

圖5 全局網絡效率的分布

表2 西直門萬壽路兩站點的比較

其中表示網絡鄰接矩陣及其稀疏矩陣，表示基于算法求得的全部平均最短路徑矩陣，表示全局網絡效率。

依照以上算法計算得正常狀態下北京市軌道交通系統全局網絡效率為0.1029，并逐一計算276個節點分別失效狀態下，全局網絡效率變化情況。計算依照各節點度值分類整理，如圖5：

顯然，雖然節點度值是表征網絡中節點重要性的主要參數，但單一節點對整體網絡效率的影響大小主要與節點的相對位置有關。例如，在整個網絡中，西直門節點度值最高，但它的失效對于整體網絡效率的影響卻小于節點度值為2的萬壽路站。這里我們用任意節點失效對應的整體網絡效率與初始網絡效率的差值所占百分比表示對整體網絡連通性的影響程度。見（表2）

在前文我們提到，北京市軌道交通系統網絡是典型的“環+放射形”結構。如圖6，從網絡整體來看，將末端支路上的節點和環狀結構內節點分別用不同顏色標記，并比較其對整體網絡效率的影響。可以較為明顯地看到，環狀結構內部節點對整體網絡效率影響較為平均且相對較小；末端支路上的節點對整體網絡效率的影響則波動較大，其中部分節點對整體網絡效率影響非常明顯。（圖6）

在同一線路中，單一節點對網絡的連通性的影響呈波浪形浮動。以地鐵一號線及八通線為例，各點對整體網絡效率的影響如圖7：

如圖所示，該線路對整體網絡效率的影響最大的兩點分別為公主墳和大望路站。分析比較節點在整個網絡的位置不難發現，兩點均處于環狀結構與放射線結構交匯位置。同時發現：在末端支路結構中，越靠近環狀結構的節點對整體網絡影響越大。這是由于環狀結構內部節點間相互聯系較為緊密，單一節點失效后，其他節點間最短路徑不會出現很大變化。結合實際情況體現在，環狀結構中任意站點由于各種原因崩潰，乘客均可以較為容易找到替代路線，利用軌道交通系統完成出行。相反，末端支路上節點失效將導致孤立節點的出現，孤立節點越多對整體網絡連通性影響越大。結合實際情況，即末端結構上的站點一旦崩潰，則可能導致靠外的線路全部癱瘓。

圖6 網絡上單個節點失效對網絡連通性的影響

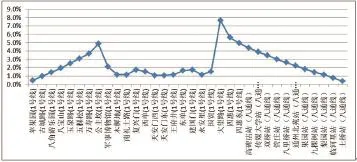
圖7 單一線路上單個節點失效對網絡連通性的影響

結語

（1）本文基于復雜網絡理論和北京市軌道交通系統實際情況，引入整體網絡連通效率這一參數更加準確地評價網絡連通性；通過比較單個站點失效狀態下與原始網絡連通效率的變化情況，分析單一站點對網絡連通性的影響大小。

（2）通過比較節點度值和節點位置對全局網絡效率的影響，得出以下結論：站點對網絡連通性的影響主要與站點的相對位置有關；通過對不同位置站點的比較發現，靠近環狀結構的末端支路站點對網絡連通性影響最大。

（3）針對這一結構性問題，相應的應急預案及可替代的公共交通方式是必要的。

（4）下一步需要研究的問題包括：結合實際客流人數和站點距離建立有權網絡，討論其對網絡連通性的影響；結合節點崩潰的傳播及恢復過程，研究軌道交通系統中結構對網絡連通性的影響。

[1] 李海峰，王煒．軌道交通網絡形態研究[J]．規劃師，2006，22(5)：85-88．

[2] 沈景炎．城市軌道交通線網規劃的結構形態基本線形和交點計算[J]．城市軌道交通研究，2008，11(6)：5-10．

[3] 張朝峰,張秀媛. 地鐵末端周邊區域通勤客流分布和出行方式選擇[J]. 都市快軌交通,2009,(04)：26-29.

[4] Crucitti P, Latora V, Marchiori M, et al. Error and attack tolerance of complex networks[J]. Nature, 2000, 406(6794)：542-542.

[5] Holme P, Kim B J, Yoon C N, et al. Attack vulnerability of complex networks.[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2002, 65(5)：634-634.

[6] 吳金閃,狄增如. 從統計物理學看復雜網絡研究[J]. 物理學進展,2004,(01)：18-46.

[7] 王云琴. 基于復雜網絡理論的城市軌道交通網絡連通可靠性研究[D]. 北京交通大學, 2008.

[8] 羅金龍, 曹成鉉, 許琰,等. 北京、上海和廣州地鐵網絡演化分析[J]. 山東科學, 2013, 26(1)：74-80.