先簡支后連續T梁橋全過程力學行為及極限承載力分析

?

先簡支后連續T梁橋全過程力學行為及極限承載力分析

朱小青，陳代海，陳淮

(鄭州大學 土木工程學院，河南 鄭州 450001)

先簡支后連續T梁橋是國內外高速公路在用的一種橋梁結構新形式，具有施工較簡易、行車條件較好且經濟合理，兼備簡支梁與連續梁橋的優點，因而在橋梁工程中得到了越來越多的應用[1-2]。目前，對該類型的橋梁進行試驗無疑是研究其極限承載力最直接有效的方法，但也存在著諸如成本較高、費工費時等缺點，尤其對于新建橋梁，不可能為研究極限承載力而進行破壞試驗，作為一種經濟、省時且行之有效的方法，數值仿真分析彌補了上述缺點[3]。然而，由于有限元分析中涉及到材料和幾何雙重非線性，計算工作量很大，且收斂困難；此外，橋梁結構的極限承載力受施工工藝和施工過程的影響很大[4-5]，目前關于先簡支后連續T梁橋結構從施工至加載到承載能力極限狀態的全過程分析并不多見。為此，本文以河南省省道S318線西張村大橋為工程背景，運用有限元軟件Midas/FEA建立了該橋的實體模型，模型考慮了幾何非線性和材料非線性，同時運用軟件提供的單元激活與鈍化功能，分別在6種工況下對先簡支后連續T梁橋結構從施工至極限破壞的受力全過程進行了模擬，根據計算得到的破壞荷載、破壞特征、荷載位移曲線以及橋梁安全系數等，評定了該橋的極限承載力。

1工程概況

西張村大橋是河南省省道S318線上一座重要的高墩橋梁，該橋橋面凈寬12 m，雙向兩車道設計，橫向由5片T梁組成，采用先簡支后連續梁橋體系，共3聯11孔。其中第一聯由4×50 m的預應力混凝土連續T梁橫向組合連接構成，總長200 m，如圖1所示。

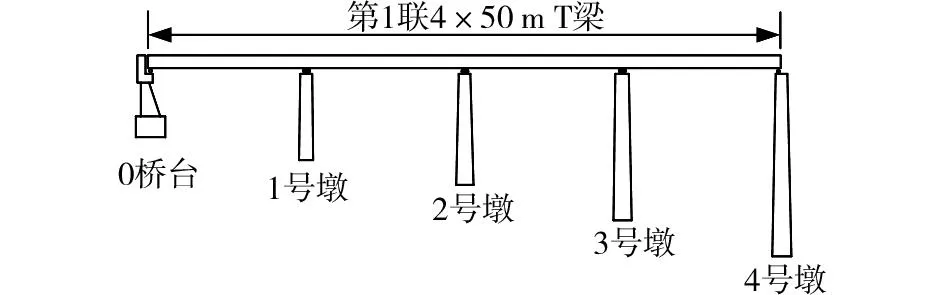
圖1　西張村大橋立面示意圖Fig.1 Facade schematic of Xizhangcun bridge

以橋梁上部結構先簡支后連續預應力混凝土T梁為研究對象，其詳細的設計參數如下。

設計荷載：公路—I級。

主梁：每片T梁高2.7 m，寬2.4 m，邊梁預制寬度為1.95 m，中梁預制寬度為1.5 m；主梁梁肋厚度支點處為0.6 m，跨中處為0.2 m(見圖2)，在支點附近4.8m范圍內逐漸加寬，在支點位置梁肋加寬至馬蹄寬。

橫隔板：全梁共設7道橫隔板，其中端橫梁2道，為實體矩形截面，中橫梁5道，橫隔梁間距為8.1 m；

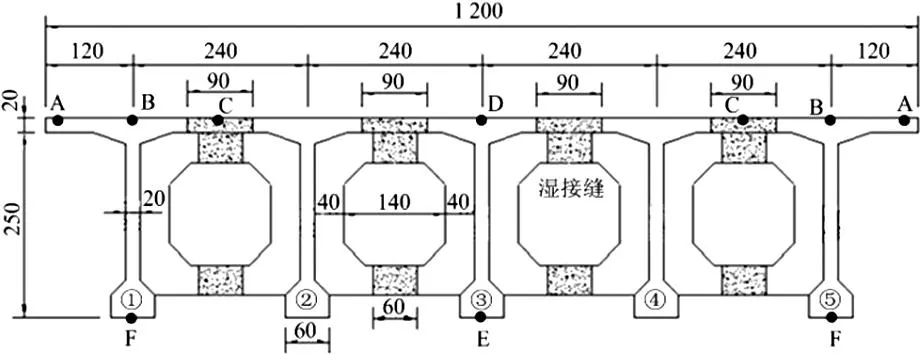
單位：cm圖2　主梁跨中橫斷面圖Fig.2 Section views of girder span

橋面現澆層：成橋后采用10 cm混凝土現澆面層+9 cm厚瀝青混凝土，模型計算時考慮4 cm的混凝土現澆層參與受力；

主梁、濕接縫及橋面現澆層混凝土的強度等級：C55；

預應力鋼絞線為低松弛高強度預應力鋼絞線，單根鋼絞線直徑為15.2 mm，公稱面積為140 mm2，標準強度為1 860 MPa，控制張拉力為標準強度的70%，采用應力、應變雙控制，后張法施工，此外，管道摩擦因數為0.25，管道偏差因數為0.001 5 m-1；

普通鋼筋：普通受力鋼筋型號為HRB335；

橋梁支座：位于1號，2號和3號橋墩中心線上的永久支座采用板式橡膠支座(GJZ 500×800×104 mm3)；位于0號橋臺和4號橋墩上、T梁端部橫隔板中心線下的永久支座采用滑板式支座(GJZF4400×450×87 mm3)；位于1號，2號和3號橋墩上、T梁端部橫隔板中心線下的臨時支座采用硫磺砂漿澆筑，下設混凝土墊塊，尺寸為400×450×104 mm3。

為便于后續分析，對橋梁橫截面上的關鍵點進行標識，并對主梁進行編號，如圖2所示。

2全橋實體有限元模型

2.1材料特性及本構關系

混凝土強度等級為C55。選用midas/FEA中總應變裂縫模型提供的多線性曲線作為混凝土受壓時的本構關系，選用常量曲線作為混凝土受拉時的本構關系[6]，如圖3所示。

預應力筋、普通鋼筋的本構關系選用von Mises模型。預應力筋的屈服強度為1 860 MPa，彈性模量為1.95×105MPa；普通鋼筋的屈服強度為335 MPa，彈性模量為2.0×105MPa，泊松比為0.3。

圖3　混凝土的非線性本構關系Fig.3 Nonlinear constitutive relations of concrete

2.2荷載及邊界條件

荷載主要考慮自重、預應力、二期恒載(如未參與結構受力的橋面現澆層和鋪裝層)等。結構自重以體積力的形式考慮；預應力采用等效節點荷載處理；二期恒載以面荷載的形式考慮[7]。

對于滑板式支座，約束其豎向和橫向的線位移；對于臨時支座和板式支座，約束其3個方向的線位移。

2.3預應力效應模擬

以張拉控制應力作為預應力筋的初始應力直接施加到預制T梁上，在橋梁全過程受力的不同階段，預應力筋的真實應力為累積應力增量與其初始應力之和。上述預應力施加方法可有效計及成橋初始狀態下材料的累積塑性變形，并能獲得較為精確的成橋初始變形和應力狀態。

2.4三維有限元模型

混凝土采用三維實體單元，鋼筋采用植入式桿單元，以橫橋向作為x軸、縱橋向作為y軸、豎直向為z軸，按實際尺寸建立全橋三維實體有限元模型。

3施工過程仿真分析及有限元模型驗證

3.1施工過程仿真

橋梁上部結構的施工分為5個階段：1)預應力混凝土T梁預制、預應力筋張拉；2)預應力混凝土T梁安裝；3)墩頂、墩頂兩側18.0 m范圍內的濕接縫及橫隔梁澆筑，頂板預應力筋張拉；4)臨時支座拆除及剩余濕接縫、橫隔梁澆筑；5) 澆筑橋面現澆層，進行橋面鋪裝。

根據上述施工過程，運用midas/FEA有限元軟件中單元的激活與鈍化功能對各施工階段進行定義和仿真模擬。對于在當前階段激活的單元，初始狀態為0；對于在前一階段已激活單元，其當前階段的初始內力為前一階段分析得到的內力，通過計算最終得到成橋初始狀態的內力。圖4為上述各施工過程的有限元網格。

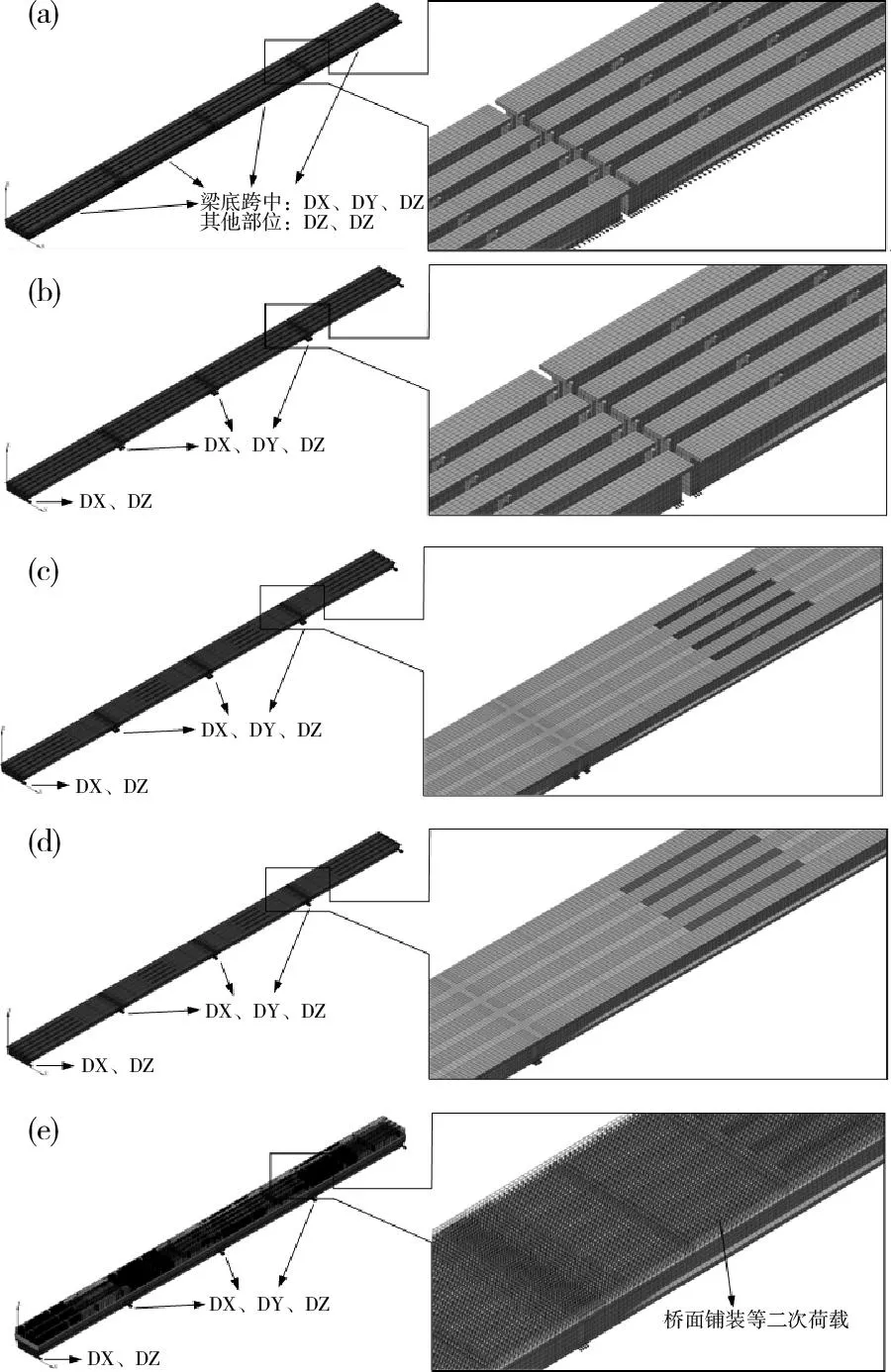
(a)第1階段施工完畢時的有限元網格；(b)第2階段施工完畢時的有限元網格；(c)第3階段施工完畢時的有限元網格；(d)第4階段施工完畢時的有限元網格；(e)第5階段施工完畢時(初始狀態)的有限元網格圖4　橋梁上部結構不同施工過程的有限元網格Fig.4 Finite element mesh of bridge superstructure indifferent construction process

3.2成橋初始狀態內力結果分析

根據成橋初始狀態的有限元計算結果，采用Matlab繪制了橫截面上關鍵點的von Mises應力沿縱橋向的分布圖，見圖5。

從圖中可見：1)截面上所有關鍵點的應力均為正值，且沿縱橋向關于2號支座截面對稱分布，上翼緣最大應力距橋臺55 m左右，位于截面D點，值為10.47 MPa，下翼緣最大應力距橋臺40 m左右，位于截面F點，值為14.67 MPa；2)截面上翼緣A，B，C和D點的應力沿縱橋向的變化趨勢基本一致，中間支座及其兩側15 m范圍內的應力呈鋸齒狀劇烈變化，其中B和D點的應力變化尤其明顯，此外，支座處應力相對較小；3)在同一橫截面位置，B點和D點的應力幾乎相等，僅在中間支座兩側15 m范圍內略有不同，并且二者均大于A點和C點的應力，C點的應力最小；4)截面下翼緣E和F點的應力沿縱橋向的變化趨勢基本一致，在同一橫截面上，F點的應力略大于E點的應力，在縱向同一點上，邊跨應力明顯大于中跨應力，支座附近應力除外。

出現上述現象的原因主要有：1)在成橋初始狀態，結構和荷載沿縱橋向均關于2號支座截面對稱，因此，截面上關鍵點的應力沿縱橋向同樣關于2號支座截面對稱；2)橋梁中間支座上翼緣兩側設有分批截斷的負預應力鋼筋，導致該區域混凝土的應力呈鋸齒狀劇烈變化，此外，支座處混凝土澆筑較晚，僅受板頂負預應力作用，因而應力較小；3)邊梁和中梁板頂負預應力筋沿板頂縱向中心線對稱分布且面積相等，因此，同一截面位于中心線上的B點和D點的應力幾乎相等，并且大于截面上翼緣其它位置處的應力，由于邊梁和中梁板頂負預應力筋截斷位置略有不同，使得中間支座兩側15 m范圍內B點和D點的應力略有不同；4)預制T梁梁底正預應力筋截面積的大小順序為邊跨邊梁>邊梁中跨>中跨邊梁>中跨中梁，使得同一截面位置邊梁梁底F點的應力大于中梁梁底E點的應力，而在縱橋向則表現為邊跨內混凝土的應力大于中跨內混凝土的應力。

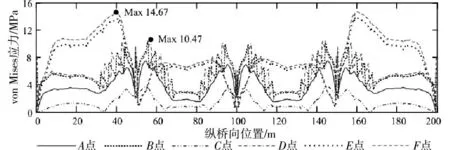
圖5　橋梁橫截面上關鍵點的von Mises應力沿縱橋向的分布Fig.5 Distribution along the longitudinal direction of thebridge of von Misesstress of the key point of the cross section

通過對西張村大橋主梁截面上、下緣的von Mises應力分析可知，成橋初始狀態下橋梁截面關鍵點均處于受壓狀態，最大壓應力14.67 MPa，說明在成橋初始狀態橋梁未出現開裂或壓碎破壞現象。此外，由上述分析可知，成橋狀態橋梁初始應力的大小及其分布規律是合理的，表明本文所建立的有限元模型是正確的、合理的。

4極限承載力仿真分析

4.1荷載及加載工況

極限承載力分析時，以上節計算得到的成橋初始狀態的內力作為初始條件，即極限承載力分析時只需在成橋初始狀態的基礎上再施加λ[8]倍的車道荷載即可。車道荷載取值分別為qk=10.5 kN/m(均布荷載)和Pk=360 kN(集中荷載)[7]。

取邊跨跨中(1-1)截面、中跨跨中(2-2)截面及梁端近支點(3-3)截面(距0號橋臺8 m，剪應力最大)為關鍵分析截面。兩車道荷載沿橫向分別考慮對稱和偏載布置，沿縱向分別布置在使結構關鍵截面產生最不利效應的同號影響線上，共計6種加載工況。

工況1：初始狀態+λ[均布荷載(偏載)+集中荷載(邊跨跨中)]，①號主梁1-1截面正彎矩最大。

工況2：初始狀態+λ[均布荷載(對稱)+集中荷載(邊跨跨中)]，直接受荷最多的②號或④號主梁1-1截面正彎矩最大。

工況3：初始狀態+λ[均布荷載(偏載)+集中荷載(中跨跨中)]，①號主梁2-2截面正彎矩最大。

工況4：初始狀態+λ[均布荷載(對稱)+集中荷載(中跨跨中)]，直接受荷最多的②號或④號主梁2-2截面正彎矩最大。

工況5：初始狀態+λ[均布荷載(偏載)+集中荷載(梁端近支點)]，①號主梁近支點3-3截面剪力最大。

工況6：初始狀態+λ[均布荷載(對稱)+集中荷載(梁端近支點)]，直接受荷最多的②號或④號主梁近支點3-3截面剪力最大。

4.2有限元計算結果及其分析

分別在上述6中工況下對該橋進行極限承載力計算，結果見圖6~10。

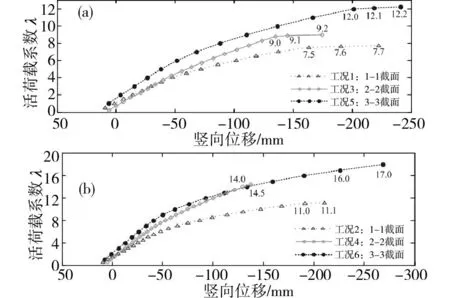
(a)偏載工況下①號梁底關鍵截面；(b)對稱荷載工況下④號梁底關鍵截面圖6　梁底關鍵截面的荷載-豎向位移曲線Fig.6 Load-vertical displacement curve of beambottom key section

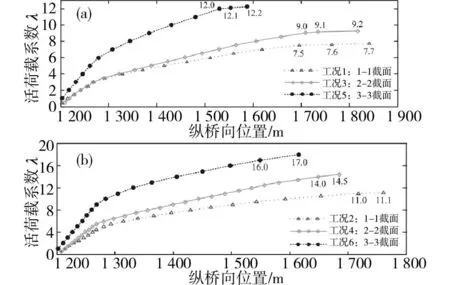
(a)偏載工況下①號梁關鍵截面；(b)對稱荷載工況下④號梁關鍵截面圖7　梁底關鍵截面預應力鋼筋的荷載-拉應力曲線Fig.7 Load-tensile stress curve of the prestressedreinforced in the key section of beam bottom

(a)工況1：偏載；(b)工況2：對稱加載圖8　1-1截面上緣混凝土縱向應力的橫向分布情況Fig.8 Lateral distribution of vertical stress in the sectionon the edge of the concrete

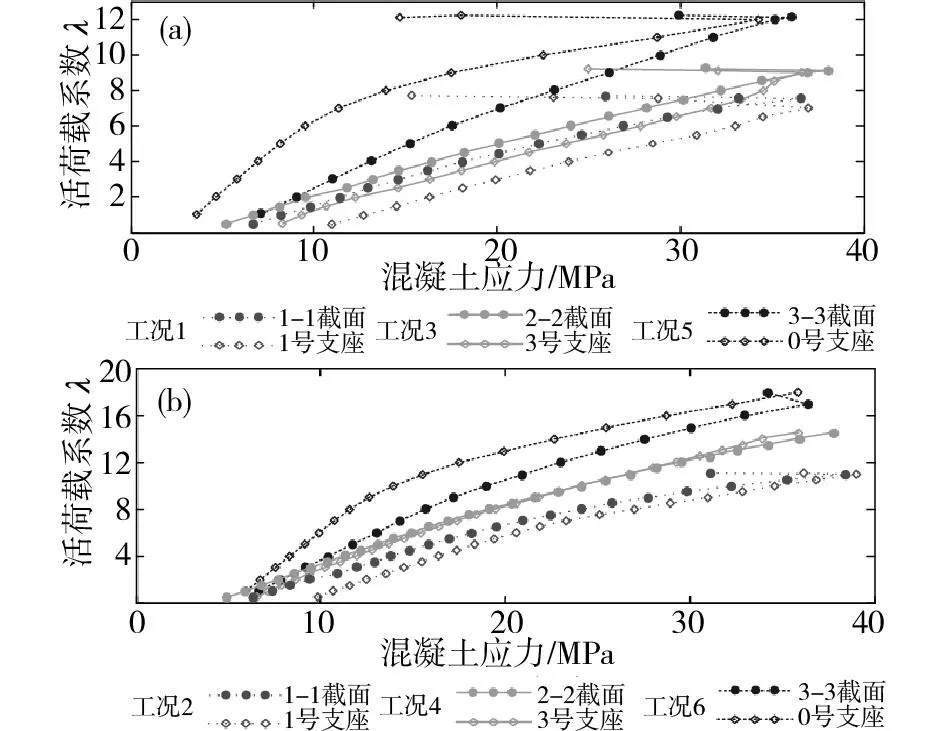
(a)偏載工況下①號梁；(b)對稱荷載工況下④號梁圖9　各工況下關鍵截面上緣、支座截面下緣中心線上混凝土的應力-荷載曲線Fig.9 Stress-load curve of the concrete in both topedge of a key section and down section bearing edgecenterline in different working condictions

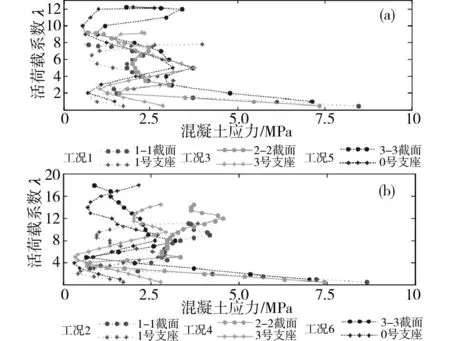
(a)偏載工況下①號梁；(b)對稱荷載工況下④號梁圖10　各工況下關鍵截面下緣、支座截面上緣中心線上混凝土的應力-荷載曲線Fig.10 Stress-load curve of the concrete in both top edgeof a key section and down section bearing edge centerlinein different working condictions

4.2.1加載全過程分析

在梁底關鍵截面底部混凝土開裂之前，整個橋梁基本處于彈性工作狀態。因此，梁底關鍵截面的豎向位移(圖6)和梁底關鍵截面預應力鋼筋的拉應力(圖7)隨λ的增加大致以線性方式增長，而梁底關鍵截面底部混凝土的應力(圖10)先線性減小后線性增大，達到最大值時混凝土開裂，對應的活荷載系數可從圖10得出；在梁底關鍵截面底部混凝土開裂之后、結構達到極限承載力之前，橋梁結構進入非線性受力階段，因此，梁底關鍵截面的豎向位移(圖6)和梁底關鍵截面預應力鋼筋的拉應力(圖7)隨λ的增加曾加速增長趨勢；當結構達到極限承載力狀態時，隨著活荷載系數的微弱增加，梁底關鍵截面的豎向位移(圖6)和梁底關鍵截面預應力鋼筋的拉應力(圖7)均快速增長，曲線的斜率幾乎為零，橋梁關鍵截面上緣、支座截面下緣中心線上的混凝土被壓碎或達到極限應力狀態，結構破壞時對應的活荷載系數可由圖6和9綜合判斷得出，各工況下結構達到極限承載力時的活荷載系數見表1。

表1　各工況下結構達到極限承載力時的活荷載系數

從表1可見，當結構達到極限承載能力狀態時，工況1，2和5對應的活荷載系數為7.5，9.0和12.0，分別小于工況2，4和6對應的活荷載系11.0，14.0和16.0，說明與對稱加載工況相比，偏載工況下橋梁更容易發生破壞。

4.2.2混凝土應力的橫向分布特征分析

以工況1、工況2為例，從圖8(a)可以看出，在偏載作用下，1-1截面上緣縱向正應力沿橫向分布十分不均勻，主要體現在2個方面：一是在同一荷載等級下濕接縫處混凝土的應力明顯小于其兩側預制主梁混凝土的應力，這與施工階段觀察到的現象一致；二是直接受荷的邊梁1-1截面上表面混凝土的應力較大，而非直接受荷的其他主梁1-1截面上表面混凝土的應力則大致線性減小；從圖8(a)可以看出，在對稱荷載作用下，同一荷載等級下濕接縫處混凝土的應力明顯小于其兩側預制主梁混凝土的應力。

此外，從圖8還可以看出，隨著荷載等級的增加，預制主梁上緣的混凝土先于濕接縫處的混凝土達到極限應力狀態，二者受力并不同步，這在一定程度上降低了橋梁結構的極限承載力。

4.2.3結構破壞特征分析

從圖9(a)可以看出，在偏載工況下，結構的破壞形式表現為①號主梁相應的支座截面底部混凝土先被壓碎，隨后相應的關鍵截面頂板混凝土被壓碎；從圖9(b)可以看出，在對稱荷載工況下，結構的破壞形式表現為④號主梁相應關鍵截面頂板的混凝土先達到極限應力狀態或先被壓碎，隨后相應支座截面底部的混凝土被壓碎。此外，從圖7中可以看出，結構破壞時，主要承受拉力的關鍵截面底板和支座截面頂板中的預應力鋼筋都沒有達到屈服應力，并且從圖8可以看出(偏載工況同工況1、對稱加載工況同工況2)，在結構發生破壞時，橋梁的橫向聯系仍具有很強的傳遞荷載的能力，并未發生破壞。這表明在所有工況作用下，結構的破壞屬于局部破壞，可以通過采取一定的措施對結構局部進行補強。

5結論

1)詳述了考慮施工過程影響的先簡支后連續梁橋三維實體有限元模型的建模方法，并由該模型精確地計算出橋梁成橋初始狀態的內力，為后續極限承載力分析提供基準計算模型；

2)當結構達到極限承載能力狀態時，工況1，2和5對應的活荷載系數為7.5、9.0和12.0，分別小于工況2，4和6對應的活荷載系數11.0，14.0和16.0，偏載工況下橋梁更容易發生破壞；

3)在偏載工況下，(邊梁)①號主梁相應的支座截面底部混凝土先被壓碎，隨后相應的關鍵截面頂板混凝土被壓碎；在對稱荷載作用下，④號主梁相應關鍵截面頂板的混凝土先達到極限應力狀態或先被壓碎，隨后相應支座截面底部的混凝土被壓碎；

4)預制主梁上緣的混凝土先于濕接縫處的混凝土達到極限應力狀態，二者受力不同步，這在一定程度上降低了橋梁結構的極限承載力。

參考文獻：

[1] 姚玲森, 項海帆, 顧安邦. 橋梁工程[M].2版. 北京: 人民交通出版社, 2008.

YAO Lingshen, XIANG Haifan, GU Anbang. Bridge construction [M].2nd edition. Beijing: China Communications Press,2008.

[2] 陳淮, 陳鵬飛, 李杰. 鋼構-連續組合梁橋主梁合攏關鍵技術[J]. 鐵道科學與工程學報,2015,12(1):113-118.

CHEN Huai, CHEN Pengfei, LI Jie, Study on key technology of the main girder closure of rigid frame -continuous combination beam bridge[J]. Journal of Railway Science And Engineering,2015,12(1):113-118.

[3] 吳光宇, 林偉, 汪勁豐, 等. 有效預應力對大跨P.C.橋梁極限承載力的影響研究[J]. 計算力學學報, 2013, 30(3): 362-369.

WU, Guangyu, LIN Wei, WANG Jinfeng, et al. Influence of effective prestress on ultimate bearing capacity for large-span prestressed concrete bridge[J].Chinese Journal of Computational Mechanics,2013,30(3):362-369.

[4] 李靜斌, 葛素娟, 陳淮. 先簡支后連續分體式箱梁橋簡支轉連續施工方法研究[J]. 世界橋梁, 2010, 1(3): 12-15.

LI Jingbin, GE Sujuan, CHEN Huai. Study of construction schemes of transferring simply-supported structure to continuous separated box girder bridge[J]. Word Bridge,2010,1(3):12-15.

[5] 易錦, 賀國京, 陸杰. 合攏及體系轉換順序對多跨鋼構-連續組合梁橋組合分析[J]. 鐵道科學與工程學報, 2013,10(5):23-27.

YI Jin, HE Guojing, LU Jie. Impact analysis of closure order and system transformation order for bridges with rigid frame-combined continuous beam[J]. Journal of Railway Science and Engineering,2013,10(5):23-27.

[6] midas FEA分析與計算原理[M]. 北京邁達斯技術有限公司.

Midas FEA Analysis and Algorithm Manual[M]. MIDAS IT(Beijing)Co,Ltd.

[7] JTG D60—2004, 公路橋涵設計通用規范[S].

JTG D60—2004, Design of highway bridges and culverts[s].

[8] 吳光宇. 大跨P.C.橋梁非線性行為的分析理論及其極限承載力計算研究[D]. 杭州：浙江大學，2006.

WU Guangyu. The nonlinearity behavior analysis theory and ultimate bearing capacity calculating method for Large-span P.C.bridges[D]. Hangzhou: Zhejiang University, 2006.

[9] Davies J M．Strain hardening. Local buckling and lateral-torsioal buckling in Plastic hinges[J]．Journal of Constructional Steel Research, 2006，12(62):27-34.

[10] Mehmet Inel, HayriBaytan Ozmen．Effects of plastic hinge properties in nonlinear analysis of Reinforced concrete buildings[J]．Engineering Structures,2006，15(28):1494-1502.

[11] Luarent Caurffiez，Joseph Ciccotelli, Blaise Conrard. Design of intelligent distributed control systems. a dependability point of view [J]．Reliability Engineering and System Safety，2004，84(1): 19-32.

[12] Campbell T I, Venkatesh Kumar R Kour. Deformation controlled nonlinear analysia of prestressed concrete continuous beams[J]．PCI Journal, 1990，25(1):42-55.

[13] AlfarabiSharif G J, AISulaimaniand B N. Ghaleb Strengthening of initiallyloaded reinforced concrete beams using FRP plates[J]．ACI Structural Journal,1994，26(23):26-31.

[14] Zienkiewinz O C.The finite element method[M]．3rd edition. London: McGraw Hill, 1977:18-34.

[15] Engin Keyder.Friction losses in prestressed steel by equivalent load method[J]． PCI Journal, 1990, 26(2)：74-77.

(編輯陽麗霞)

摘要：為研究先簡支后連續T梁橋從施工至極限破壞的全過程受力性能，以河南省省道S318線西張村大橋為工程背景，運用有限元軟件midas/FEA建立同時考慮幾何非線性和材料非線性影響的全橋三維實體模型，分別在6種工況下進行了仿真分析研究。研究結果表明：橋梁達到極限承載力時，偏載工況下的活荷載系數小于相應對稱荷載工況下的活荷載系數；偏載工況下邊梁相應的支座截面底部混凝土先被壓碎，對稱荷載作用下，受荷位置主梁相應關鍵截面頂板的混凝土先被壓碎；預制主梁上緣的混凝土先于濕接縫處的混凝土達到極限應力狀態，二者受力不同步。

關鍵詞：先簡支后連續T梁橋；極限承載力；有限元；全過程受力

Study on full loading process performance of simply supported continuous T-beam bridgeZHU Xiaoqing, CHEN Daiha, CHEN Huai

(School of Civil Engineering, Zhengzhou University, Zhengzhou 450001, China)

Abstract:The paper studied the stress performance of simply supported continuous T-beam bridge from construction stage to the ultimate failure. By considering the material and geometric nonlinear conditions, the finite element software Midas/FEA was used to simulate the three-dimensional solid model of a full-bridge under the six kinds of conditions in the engineering background of Xizhangcun Bridge in Henan Province Highway S318. The results showed that: The live load factor in unbalance loading working condition was less than that of balanced when the bridge reach the ultimate bearing capacity; The concrete in the bottom of support cross-section of the spandrel beam was crushed firstly in unbalance loading working condition; In the condition of balance loading working the concrete in the top of the key sections of girder at the load position was crushed firstly; The concrete at the top of the girder precast reached the critical stress earlier than in the wet-joint and their force were asynchronous.

Key words：simply supported continuous T-beam bridge; ultimate bearing capacity; finite element; full loading process

中圖分類號：U448.14

文獻標志碼：A

文章編號：1672-7029(2016)01-0089-07

通訊作者：陳淮(1962-)，男，河南淮陽人，教授，博士，從事橋梁工程研究；E-mail: chenh@zzu.edu.cn

基金項目：國家自然科學基金資助項目(51408555)；河南省交通運輸廳科技項目(2008P250)

收稿日期：*2015-06-24