Massive MIMO上行系統(tǒng)能效資源分配算法

江愛珍，曾桂根

(南京郵電大學(xué)，江蘇 南京 210003)

Massive MIMO上行系統(tǒng)能效資源分配算法

江愛珍，曾桂根

(南京郵電大學(xué)，江蘇 南京 210003)

研究了在認(rèn)知無線電Ad Hoc網(wǎng)絡(luò)(CRAHNs)中基于大規(guī)模多輸入多輸出(Massive MIMO)上行系統(tǒng)的能效資源分配算法。簇頭采用迫零(ZF)接收，且考慮在電路功率消耗、各節(jié)點(diǎn)的最小數(shù)據(jù)速率以及最大發(fā)射功率的情況下，建立基于能效下界的非凸優(yōu)化模型。根據(jù)分?jǐn)?shù)規(guī)劃的性質(zhì)，將能效最優(yōu)化問題中分?jǐn)?shù)形式轉(zhuǎn)化為減式形式，從而利用凸優(yōu)化求解最優(yōu)接收天線數(shù)和各節(jié)點(diǎn)發(fā)射功率來獲得最大能效。仿真結(jié)果表明，所提算法在能效上近似最優(yōu)值，能夠滿足各節(jié)點(diǎn)最小數(shù)據(jù)速率及最大功率的約束條件，且能以較小的迭代次數(shù)收斂到最優(yōu)能效性能。

Massive MIMO；能效；資源分配；上行系統(tǒng)；分?jǐn)?shù)規(guī)劃；CRAHNs

0 引 言

認(rèn)知無線電自組網(wǎng)絡(luò)(CRAHNs)是一種具有頻譜感知功能的分布式多跳移動(dòng)自組網(wǎng)絡(luò)，無固定中心節(jié)點(diǎn)，每個(gè)節(jié)點(diǎn)都具備路由、轉(zhuǎn)發(fā)功能，組網(wǎng)方便快捷[1]。因此CRAHNs在軍事、民用救災(zāi)、搶險(xiǎn)、貨運(yùn)碼頭等場合獲得了廣泛應(yīng)用。如圖1所示，CRAHNs中節(jié)點(diǎn)主要包括手持設(shè)備(單天線節(jié)點(diǎn),SN)、單兵背負(fù)式設(shè)備(多天線節(jié)點(diǎn),MN)和車載設(shè)備(大規(guī)模天線節(jié)點(diǎn),MM)，其中SN和MN作為普通節(jié)點(diǎn)(以下簡稱節(jié)點(diǎn))，MM作為簇頭。此時(shí)，簇頭和節(jié)點(diǎn)可分別看作是蜂窩網(wǎng)中的基站和用戶。因此，雖然目前CRAHNs網(wǎng)絡(luò)下大規(guī)模MIMO的研究成果很少，但可類比蜂窩網(wǎng)下的大規(guī)模MIMO問題。

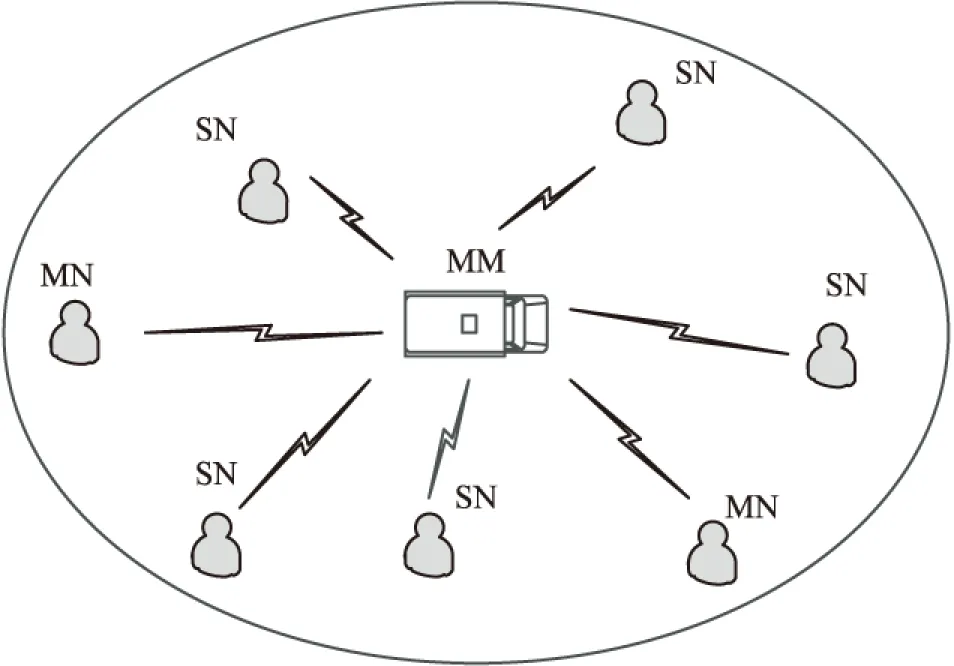
圖1 系統(tǒng)模型

大規(guī)模多輸入多輸出(Massive MIMO)技術(shù)在增強(qiáng)頻譜和能量效率方面具有很大優(yōu)勢[2-8]，目前蜂窩網(wǎng)下的Massive MIMO技術(shù)已被高度關(guān)注[9-13]。文獻(xiàn)[5]研究推導(dǎo)了多用戶Massive MIMO系統(tǒng)在上行分別采用最大比合并(MRC)、迫零(ZF)和最小均方誤差(MMSE)檢測時(shí)的容量下界。文獻(xiàn)[6]在采用MRC和ZF檢測的情況下，研究了只考慮最大系統(tǒng)容量時(shí)，完全已知和不完全已知信道狀態(tài)信息(CSI)的上行鏈路導(dǎo)頻長度、導(dǎo)頻功率和數(shù)據(jù)功率分配。文獻(xiàn)[7]研究了多節(jié)點(diǎn)Massive MIMO系統(tǒng)下行的能效資源分配，在考慮用戶服務(wù)質(zhì)量(QoS)時(shí)，提出了用戶速率分配、基站子載波和天線分配的策略，并給出了相應(yīng)的迭代算法。文獻(xiàn)[9]通過設(shè)計(jì)Massive MIMO系統(tǒng)的發(fā)送幀結(jié)構(gòu)來提高頻譜效率。

文中在CRAHNs中應(yīng)用Massive MIMO技術(shù)來提高網(wǎng)絡(luò)的通信性能并降低能量消耗。假設(shè)接收端完全已知信道狀態(tài)信息(CSI)，文中主要研究簇頭和節(jié)點(diǎn)之間的上行資源分配算法，將各節(jié)點(diǎn)的最大發(fā)射功率以及QoS需求作為約束條件，提出了基于能效下界的目標(biāo)函數(shù)，根據(jù)分?jǐn)?shù)規(guī)劃的性質(zhì)，將目標(biāo)函數(shù)中的分?jǐn)?shù)問題轉(zhuǎn)化為減式最優(yōu)化問題，從而降低計(jì)算復(fù)雜度。

1 系統(tǒng)模型及問題描述

1.1 系統(tǒng)的吞吐量下界

文中主要研究CRAHNs中Massive MIMO的上行系統(tǒng)，簇頭配置M根天線，已有研究表明，多用戶MassiveMIMO系統(tǒng)的信道快衰落系數(shù)滿足零均值，且是獨(dú)立同分布(independentandidenticallydistributed,i.i.d.)[14]。因此下面都采用瑞利衰落信道。

首先討論MN與簇頭間通信問題的處理。為方便分析說明，假設(shè)MN只配置有2根天線，且2根天線聯(lián)合編碼，功率消耗為2P，此時(shí)MN的速率為：

(1)

而2根自主單天線SN功率消耗分別為P時(shí)，總速率為：

其中，hi是第i個(gè)SN節(jié)點(diǎn)(或i根天線)到簇頭的信道矩陣；N0是噪聲方差。

根據(jù)式(1)、(2)可知，RMN=Rsum，因此在上述假設(shè)條件下，MN與簇頭間的通信可等效成2個(gè)SN節(jié)點(diǎn)與簇頭間的通信問題。下文都是基于簇頭和SN間的上行系統(tǒng)來研究。

K個(gè)節(jié)點(diǎn)在相同的時(shí)間-頻率資源下發(fā)送數(shù)據(jù)(M≥K+1)，則簇頭接收的信號為：

y=P1/2Gx+n

(3)

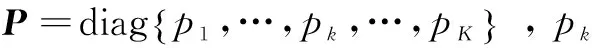
G可表示為：

G=HD1/2

(4)

其中，H是簇頭和K個(gè)節(jié)點(diǎn)間的M×K的快衰落系數(shù)矩陣；D=diag{β1,…,βk,…,βK}，βk表示節(jié)點(diǎn)k的大尺度衰落因子。

文中采用ZF檢測得：

r=AHy=P1/2AHGx+AHn

(5)

其中，A為ZF檢測矩陣；rk和xk分別是矩陣r和x的第k個(gè)元素，則

其中，ak和gk分別是矩陣A和G的第k列。

式(6)中3項(xiàng)分別是節(jié)點(diǎn)k的期望信號、其他用戶的干擾和噪聲。并假設(shè)信道是遍歷的，則節(jié)點(diǎn)k遍歷的上行速率為：

假設(shè)簇頭端完全已知G，則檢測矩陣A=G(GHG)-1，式(7)變換為：

Rk=

(8)

根據(jù)Jensen不等式可得其下界為：

log2(1+βkpk(M-K))

(9)

如圖2所示，理論值和吞吐量下界值分別是式(7)和式(9)的求和結(jié)果，可看出推導(dǎo)的吞吐量下界值與理論值非常接近。因此，1.2節(jié)中的系統(tǒng)吞吐量用下界值來代替理論值。

圖2 系統(tǒng)的吞吐量比較(K=10)

1.2 基于能效下界的最優(yōu)化模型

根據(jù)1.1節(jié)中的吞吐量下界的推導(dǎo)，則系統(tǒng)總吞吐量的下界為：

(10)

系統(tǒng)的總功率消耗包括所有節(jié)點(diǎn)發(fā)射功率和簇頭端固定電路消耗兩部分，表示為：

其中，PC是每根天線固定電路功率消耗，包括A/D轉(zhuǎn)換、接收濾波器、混頻器、低噪聲放大器等。系統(tǒng)的能效下界函數(shù)可表示為：

除考慮能效以外，在實(shí)際CRAHNs網(wǎng)絡(luò)中，不同設(shè)備的最大功率和數(shù)據(jù)速率要求都不同，因此文中還考慮了節(jié)點(diǎn)的最大發(fā)射功率限制以及QoS要求。基于以上分析，可得到多節(jié)點(diǎn)MassiveMIMO上行系統(tǒng)中能效資源分配的約束最優(yōu)化問題，即：

(13)

2 多節(jié)點(diǎn)Massive MIMO上行系統(tǒng)中能效資源分配算法

上述能效下界函數(shù)是分?jǐn)?shù)形式且非凸，因此可采用文獻(xiàn)[14]中分?jǐn)?shù)規(guī)劃的性質(zhì)將其轉(zhuǎn)化為減數(shù)形式，式(12)可轉(zhuǎn)化為：

其中：

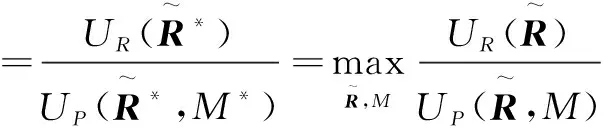
(14)

因此，式(13)中的約束最優(yōu)化問題可轉(zhuǎn)化為：

(15)

假設(shè)

則函數(shù)f的Hesse矩陣為：

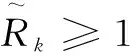
其中，λk≥0和μk≥0分別對應(yīng)式(15)中兩個(gè)約束條件的Lagrangian乘子。因此，式(15)的對偶問題可表示為

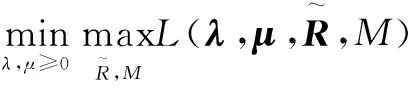
給定λ和μ，各節(jié)點(diǎn)的最優(yōu)發(fā)射速率和簇頭天線數(shù)為：

(16)

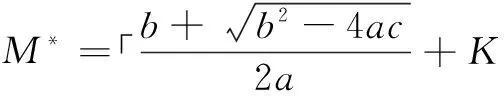
(17)

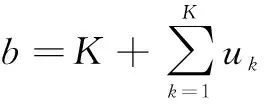
Lagrangian乘子迭代式如下：

(18)

(19)

其中，[x]+=max{0,x}；i表示迭代次數(shù)；ε表示迭代步長。

其中，α為常數(shù)，用來調(diào)整收斂速度。

用Dinkelbach迭代方法[14]求解最優(yōu)化問題,具體迭代資源分配算法如下：

(2)設(shè)置迭代次數(shù)n=0,q*=0；

(6)Endwhile

3 仿真結(jié)果與分析

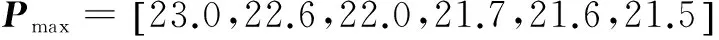
圖3 不同節(jié)點(diǎn)數(shù)的能效以及天線數(shù)比較

從中可看出：

(1)隨著節(jié)點(diǎn)數(shù)的增加，系統(tǒng)的能效性能明顯提高，因?yàn)楣?jié)點(diǎn)數(shù)的增加可使系統(tǒng)的節(jié)點(diǎn)分集特性更為明顯。并且文中算法接近窮舉算法的能效性能。

(2)因?yàn)楣?jié)點(diǎn)最低速率要求及最大功率限制，使得有約束條件時(shí)系統(tǒng)能效相較于無約束時(shí)有所降低。

圖3的下圖是與上圖相同設(shè)置時(shí)的天線數(shù)比較。從中可以看出，隨著用戶數(shù)的增加，BS端所配置天線數(shù)明顯增加，與式(17)相吻合。有約束比無約束時(shí)天線數(shù)有很大增加，這是因?yàn)樵诠?jié)點(diǎn)的最大功率Pmax較小時(shí)，又要保證一定的最小速率Rmin，只能靠增加簇頭端天線數(shù)來降低節(jié)點(diǎn)發(fā)射功率、提高發(fā)射速率。

圖4給出了不同節(jié)點(diǎn)時(shí)兩種情況下系統(tǒng)的頻譜效率。

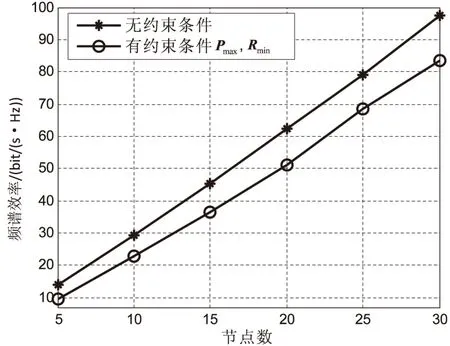
圖4 不同節(jié)點(diǎn)數(shù)時(shí)的頻譜效率比較

從圖4中可以看出，隨著節(jié)點(diǎn)數(shù)的增加，系統(tǒng)的頻譜效率顯著提高。圖4是保證最小速率Rmin為1 bit/(s·Hz)時(shí)，設(shè)置不同Pmax的結(jié)果，此時(shí)兩種情況下簇頭天線數(shù)近似，但是明顯有約束比無約束時(shí)的頻率效率要小，這是因?yàn)镻max值的約束設(shè)置得較小。

圖5給出了文中迭代算法在節(jié)點(diǎn)數(shù)為15、不同發(fā)射功率Pmax下各迭代次數(shù)的能效比較。

圖5 不同最大發(fā)射功率時(shí)各迭代次數(shù)的能效比較(K=15)

從圖5中可看出，最大功率越大，系統(tǒng)的能效越大，但當(dāng)最大功率達(dá)到一定值時(shí)，并不影響最大能效值。此外，在迭代次數(shù)為5時(shí)，即達(dá)到最大能效的95%，可在迭代次數(shù)10內(nèi)得到能效最大值。

圖6的上圖給出了在最小速率設(shè)置為1 bit/(s·Hz)時(shí)，無約束和有約束時(shí)節(jié)點(diǎn)1～5的頻譜效率比較。從中可以看出，無約束時(shí)節(jié)點(diǎn)1～5的頻譜效率相同，這是因?yàn)闆]有最大功率的限制，這時(shí)節(jié)點(diǎn)所消耗功率也相同。而有約束時(shí)節(jié)點(diǎn)1～5因最大功率的不同而不同，并且最大功率越大，相應(yīng)的頻譜效率也越大，節(jié)點(diǎn)的功率消耗如圖6的下圖所示。

圖6 節(jié)點(diǎn)1～5在兩種情況下的頻譜效率和功率消耗對比(β=1，Pmax=[0.5,0.2,0.15,0.4,0.3] W)

表1是相同最大功率和最小速率限制下，不同的大尺度衰落因子β時(shí)的節(jié)點(diǎn)速率和功率消耗。

表1 不同β時(shí)的節(jié)點(diǎn)速率和功率消耗

從表1中可以看出，β越大，功率消耗以及速率都越大。這是因?yàn)樾诺罈l件好的節(jié)點(diǎn)會(huì)被分配更多的資源。

4 結(jié)束語

文中在CRAHNs網(wǎng)絡(luò)中，研究了基于MassiveMIMO上行系統(tǒng)的能效資源分配算法。在簇頭端完全已知CSI時(shí)，采用ZF檢測，建立了最大能效下界的非凸優(yōu)化模型。因?yàn)樵贑RAHNs網(wǎng)絡(luò)，各移動(dòng)設(shè)備的最大功率和最小數(shù)據(jù)功率不同，因此增加了約束條件。根據(jù)分?jǐn)?shù)規(guī)劃的性質(zhì)，將能效函數(shù)分?jǐn)?shù)形式轉(zhuǎn)化為減式形式，利用凸優(yōu)化求解獲得最大能效。理論分析和仿真結(jié)果表明，所提算法在能效上近似最優(yōu)值，滿足節(jié)點(diǎn)的最小數(shù)據(jù)速率及其最大功率限制，且能以較小的迭代次數(shù)收斂到最優(yōu)能效性能。

[1]AkyildizIF,LeeWon-Yeol,ChowdhuryKR.CRAHNs:cognitiveradioadhocnetworks[M].[s.l.]:ElsevierPublishingHouse,2009:810-836.

[2]KumarR,GurugubelliJ.HowgreentheLTEtechnologycanbe?[C]//Procof2ndinternationalconferenceonwirelesscommunication,vehiculartechnology,informationtheoryandaerospace&electronicsystemstechnology.[s.l.]:[s.n.],2011.

[3]ZhouXingyu,BaiBo,ChenWei.AntennaselectioninenergyefficientMIMOsystems:asurvey[J].ChinaCommunications,2015,12(9):162-173.

[4]LarssonEG,TufvessonF,EdforsO,etal.MassiveMIMOfornextgenerationwirelesssystems[J].IEEECommunicationMagazine,2014,52(2):186-195.

[5]NgoHQ,LarssonEG,MarzettaTL.EnergyandspectralefficiencyofverylargemultiuserMIMOsystems[J].IEEETransactionsonCommunications,2013,61(4):1436-1449.

[6]KhansefidA,MinnH.AsymptoticallyoptimalpowerallocationformassiveMIMOuplink[C]//Procof2014IEEEglobalconferenceonsignalandinformationprocessing.[s.l.]:IEEE,2014.

[7]NgDWK,LoES,SchoberR.Energy-efficientresourceallocationinOFDMAsystemswithlargenumbersofbasestationantennas[J].IEEETransactionsonWirelessCommunications,2012,11(9):3292-3304.

[8]MiaoGuowang,HimayatN,LiGY.Energy-efficientlinkadaptationinfrequency-selectivechannels[J].IEEETransactionsonCommunications,2010,58(2)：545-554.

[9]DaiLinglong,WangZhaocheng,YangZhixing.Spectrallyefficienttime-frequencytrainingOFDMformobilelarge-scaleMIMOsystem[J].IEEEJournalonSelectedAreasinCommunications,2013,31(2):251-263.

[10]FuLiqun,ZhangJ,HuangJianwei.EnergyefficienttransmissionsinMIMOcognitiveradionetworks[J].IEEEJournalonSelectedAreasinCommunications,2013,31(11):2420-2431.

[11]CuiShuguang,GoldsmithAJ,BahaiA.Energy-efficiencyofMIMOandcooperativeMIMOtechniquesinsensornetworks[J].IEEEJournalonSelectedAreasinCommunications,2004,22(6):1089-1098.

[12]RusekF,PerssonD,LauBK,etal.ScalingupMIMO:opportunitiesandchallengeswithverylargearrays[J].IEEESignalProcessingMagazine,2013,30(1):40-60.

[13]LeNP,TranLC,SafaeiF.Adaptiveantennaselectionforenergy-efficientMIMO-OFDMwirelesssystems[C]//Procof17thinternationalsymposiumonwirelesspersonalmultimediacommunications.[s.l.]:[s.n.],2014.

[14]DinkelbachW.Onnonlinearfractionalprogramming[J].ManagementScience,1967,13:492-498.

Energy-efficient Resource Allocation for Massive MIMO Uplink Systems

JIANG Ai-zhen,ZENG Gui-gen

(Nanjing University of Posts and Telecommunications，Nanjing 210003，China)

An energy-efficient resource allocation algorithm for Massive MIMO uplink system in Cognitive Radio Ad Hoc Networks (CRAHNs) is studied.In the case of a Zero-Forcing (ZF) receiver in cluster,the considered problem is modeled as a non-convex optimization based on energy-efficient lower bound.Furthermore,the optimization takes into account the circuit power consumption,minimum required data rate and maximum required power of each node.According to the properties of fractional programming,the resulting energy-efficient optimization in the fractional form is transformed into subtractive form.Convex optimization is exploited to obtain the numbers of antennas and optimal transmit power of each node which lead to maximum energy efficiency.Simulation shows that the proposed algorithm approximates the optimal value of the energy efficiency,satisfies the minimum data rate and the maximum power constraint,and converges to energy-efficient optimization in a small number of iterations.

Massive MIMO;energy efficiency;resource allocation;uplink systems;fractional programming;CRAHNs

2015-12-22

2016-04-20

時(shí)間：2016-09-19

國家自然科學(xué)基金面上項(xiàng)目(61471202)

江愛珍(1990-)，女，碩士研究生，研究方向?yàn)榇笠?guī)模MIMO資源分配和信道估計(jì)；曾桂根，副教授，碩士生導(dǎo)師，研究方向?yàn)镸IMO通信信號處理、協(xié)作通信、綠色通信等。

http://www.cnki.net/kcms/detail/61.1450.TP.20160919.0839.014.html

TP301.6

A

1673-629X(2016)10-0200-05

10.3969/j.issn.1673-629X.2016.10.044