基于壓縮感知的自適應導頻信道估計
孫 君,高 杰
(南京郵電大學 通信與信息工程學院,江蘇 南京 210003)
基于壓縮感知的自適應導頻信道估計
孫 君,高 杰
(南京郵電大學 通信與信息工程學院,江蘇 南京 210003)
在無線通信系統中,如何提升信道估計的準確度對提升無線通信的系統性能至關重要。在信道估計中,導頻開銷占據了較多的頻譜資源,且傳統的信道估計算法不能根據信道狀態實時調整信道估計中所需要的導頻數量。而壓縮感知信道估計算法,可以利用無線信道的稀疏特性,提高信道估計的精確度,減少導頻子載波的開銷。基于此特點,將壓縮感知與信道估計相結合,研究了基于壓縮感知的稀疏度未知情況的信道估計,并提出一種適用于LTE-A系統的導頻自適應信道估計算法。仿真結果表明:與傳統的LS信道估計和LMMSE信道估計相比,所提出的導頻自適應算法能夠將導頻數量減少40%左右,并能獲得更準確的信道估計性能。
壓縮感知;信道估計;自適應;導頻
1 概 述
作為第四代移動通信的代表,LTE-A采用了正交頻分復用(Orthogonal Frequency Division Multiplexing,OFDM)等關鍵物理層傳輸技術。雖然針對于LTE-A系統的研究已經趨近成熟,但是LTE-A信道估計技術仍然是一個主要的研究問題。OFDM技術雖然能夠有效解決多徑效應和信道頻率選擇特性的問題,但在接收端OFDM需要通過精確的信道狀態信息進行相干解調,因此精確的信道估計在OFDM系統中起著舉足輕重的作用[1]。研究表明[2],高速寬帶無線通信中由于多徑效應的影響,信號的能量將集中在無線信道主要的幾條可分辨路徑中,在時域上具備稀疏特性。
在傳統的信道估計中,諸如最小二乘法(Least Square,LS)和線性最小均方誤差(Linear Minimum Mean Square Error,LMMSE)以及維納濾波等典型的信道估計技術[3-5],都利用了導頻信息對信道進行估計,且都沒有考慮到信道的稀疏特性。隨著近幾年壓縮感知理論[6-7]的興起,利用信道的稀疏特性進行信道估計成為通信領域的一個研究熱點。對于稀疏信道,壓縮感知的引入不僅可以降低導頻開銷,同時也能夠更準確地獲得信道狀態信息。
針對于壓縮感知在信道估計中的應用,已經有很多學者對此進行了研究。文獻[8]研究了信道稀疏度已知條件下OFDM系統的稀疏信道估計算法。但在實際信道中稀疏度是未知的,文獻[9]提出一種稀疏度自適應匹配追蹤算法(Sparsity Adaptive Matching Pursuit,SAMP),能夠在稀疏度未知的情況下獲得當前信號的稀疏度并精確重構原始信號。傳統的信道估計中,諸如LS和LMMSE算法在導頻點均勻分布的時候能夠取得最優的信道估計性能。而在壓縮感知理論中,隨機分布的采樣點才能夠取得最優的重構性能。文獻[10-11]對壓縮感知信道估計中導頻子載波的位置進行了研究。
在現有研究的基礎上,文中提出了一種基于壓縮感知的導頻自適應信道估計算法。在信道稀疏度未知的情況下,首先通過壓縮感知算法估計當前信道的稀疏度和信道狀態信息,然后自適應調整下一幀傳輸信號的導頻密度信息。與現有研究中導頻密度在信號傳輸開始時就已經設定且保持固定不同,文中提出的自適應導頻信道估計能夠根據前一幀反饋的信道狀態信息,更加靈活地調整下一幀中所需要的最小導頻密度,減少不必要的導頻開銷。仿真結果表明,與現有方法對比,通過使用導頻自適應算法,在降低導頻開銷的同時能夠獲得更精確的信道估計性能。
2 壓縮感知和系統模型
2.1 壓縮感知
壓縮感知(Compressive Sensing)理論[12-14]的主要思想是利用信號的稀疏性以遠低于奈奎斯特采樣率的采樣方式對信號進行采樣,并通過重構算法實現對原始信號的精確重構。壓縮感知問題可以歸結為對式(1)中的x進行求解:
y=Φx=Φ(Ψα)
(1)
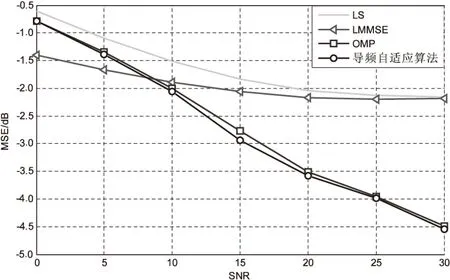
其中,x為N×1維的稀疏信號向量,在N×N維稀疏基Ψ上可以稀疏表示,其稀疏度為K;y為M×1維的觀測值;Φ為M×N維的觀測矩陣;K 壓縮感知的基本問題主要包括以下三個方面:信號的稀疏表示;觀測矩陣的設計;信號的重構算法,即如何從觀測值y中恢復信號x。 式(1)中,未知數的個數遠大于方程的個數。為實現信號的精確重構,對于滿足‖x‖0≤K的x,觀測矩陣Φ必須滿足約束等距(RestrictedIsometryProperty,RIP)[6]準則: (2) 從觀測值y中恢復信號x的問題,可以轉化為基于0-范數的最優化求解問題: min‖ΦTx‖0s.t.y=Φx (3) 式(3)是一個基于0-范數的非凸優化問題。由于0-范數問題是無解的,在實際中0-范數問題被轉化為可解的l-范數的凸優化問題。對于式(3)的求解過程就是壓縮感知的重構過程。常見的重構算法[6]有基追蹤(BasisPursuit,BP)、正交匹配追蹤算法(OrthogonalMatchingPursuit,OMP)以及SAMP等典型算法。考慮到算法復雜度和信號重建的性能,OMP算法在信道估計中應用的更為廣泛。 2.2 系統模型 (4) Yp=XpH+Np=XpFph+Np (5) 其中,Yp、Xp、Np和Fp分別表示導頻位置的接收值、發送值、信道加性噪聲和導頻位置相對應的FFT矩陣的行向量。 根據式(5)可以獲知導頻處的頻域信道沖擊響應: (6) 式(6)可以通過壓縮感知的重構算法對信道的時域沖擊響應值h進行求解。 3.1 算法描述 在傳統的信道估計中,導頻的數量和模式都是預先設定,以保證在信道環境較差時依然能獲得較好的信道估計性能。但這種預設的導頻并不能根據信道環境的變化調整導頻密度,導致信道環境較好時存在過多的頻譜資源用于不必要的導頻傳輸。 針對傳統信道估計的這一缺點,文中提出一種導頻自適應的壓縮感知信道估計方法,可以在信道稀疏度未知的情況下對信道做準確估計并指示下一幀的導頻密度,從而在降低導頻開銷的同時提升信道估計性能。其主要思想就是根據信道稀疏度的變化,實時調整下一幀信號中所需要的導頻數量。圖1給出了所提算法的基本流程。 圖1 基于壓縮感知的導頻自適應信道估計的基本過程 首先,接收端接收到第N-1幀信號后,提取當前幀的導頻信息,根據LS算法獲得當前子幀的導頻位置的頻域響應值;其次,在信道稀疏度未知的情況下,通過壓縮感知的重構算法估計當前子幀的信道稀疏度和信道狀態信息;最后,根據估計得到的信道稀疏度評估當前信道狀況,并根據式(7)計算下一幀信號所需要的最小導頻密度,并反饋給發送端。 根據文獻[6],要想精確地從采樣值中重構原始信號,測量值的維度必須滿足: (7) 其中,N為已知量;K則由壓縮感知的重構算法獲得。 3.2 SAMP算法 文中采用文獻[9]中的SAMP算法,在信道稀疏度未知的情況下估計信道稀疏度。基本過程如下: 首先,對信道殘差r(觀測值與觀測值之間的差值)、支撐索引集Λ和候選集C、迭代次數i和階段stage進行初始化。其中,r0=Yp,Λ=?表示每次迭代中與接收值Yp相關性較大的觀測矩陣的索引,C=?表示每階段與接收值Yp相關性較大的觀測矩陣的索引,i=stage=1;循環過程如下: Step1:計算殘差與觀測矩陣每一列Aj的內積〈Aj,ri-1〉,選取內積最大的s個值的索引記為Js; Step2:更新候選集Ci=Λi-1∪Js; Step4:判決是否‖ri‖≤ε,如果是則跳出循環;否則判斷是否‖ri‖≥‖ri-1‖,是則更新stage=stage+1,k=stage×s,否則Λi=Λ,i=i+1。 本節通過蒙特卡羅仿真驗證分析所提算法的性能,并給出仿真結果分析。仿真參數設置如下:OFDM符號子載波數為1 024,采用3GPP協議36.101中的EVA信道,循環前綴長度160,采用QAM調制,并選取導頻間隔為6作為標準的導頻參考,對于每個符號進行600次仿真。仿真中分別以LS、LMMSE和信道稀疏度已知的OMP重構算法作為對比。 圖2主要分析了不同導頻模式下的信道估計性能隨信噪比(SignalNoiseRatio,SNR)變化的均方誤差(MeanSquareError,MSE)曲線。圖中實線表示導頻間隔為6時的性能曲線,虛線表示導頻間隔為10時的性能曲線(根據式(7)中c的取值不同而略有不同,此處c為1.65)。 圖2 不同導頻模式下的MSE曲線 從圖中可以得知,LS、LMMSE的估計性能隨著導頻數量的減少而大幅降低。與此同時,采用隨機導頻模式的OMP重構算法進行的信道估計性能保持不變,而采用均勻導頻模式的OMP算法,在不同導頻間隔時性能差距較大。由分析可知,在導頻間隔為10時,導頻數量仍然能夠滿足式(7)的要求;采用均勻導頻模式時,導頻間隔為10時所選用的測量矩陣的相關性較大,從而降低了信道估計的性能。 圖3給出了不同信噪比下導頻自適應算法信道估計性能。圖中OMP采用隨機的導頻模式,LS和LMMSE算法采用均勻導頻模式。 從仿真結果可以看出,導頻自適應算法根據前一幀估計的稀疏度,及時調整當前幀的密度減小導頻開銷的同時,能夠達到與稀疏度已知的OMP算法近乎一致的性能。 圖4給出了導頻自適應算法估計的信道稀疏度與真實稀疏度對比的情況。 圖3 導頻自適應算法性能 圖4 不同SNR下的稀疏度估計性能 文中主要研究了一種導頻自適應的壓縮感知信道估計算法。該算法通過一種反饋機制實時反映當前信道狀態,為下一幀信號的導頻設計提供最優方案,在減少導頻數量的同時降低信道估計誤差,提升信道估計的準確度。仿真結果表明,與傳統的信道估計所需導頻數量相比,導頻自適應的壓縮感知信道估計算法能夠減少40%左右的導頻開銷。 [1]GhassemiA,GhasemnezadH,GulliverTA.CompressivesensingbasedestimationofOFDMnonlineardistortion[C]//Procof2014IEEEinternationalconferenceoncommunication.[s.l.]:IEEE,2014:5055-5059. [2] 趙 競,王 玲.壓縮感知理論在OFDM稀疏信道估計中的應用[J].通信技術,2012,45(3):13-15. [3] 張繼東,鄭寶玉.基于導頻的OFDM信道估計及其研究進展[J].通信學報,2003,24(11):116-124. [4] 王東明,高西奇,尤肖虎,等.寬帶MIMO-OFDM系統信道估計算法研究[J].電子學報,2005,33(7):1254-1257. [5]HoeherP,KaiserS,RobertsonP.Two-dimensionalpilotsymbolaidedchannelestimationbyWienerfiltering[C]//ProcofIEEEinternationalconferenceonacoustics,speech,andsignalprocessing.[s.l.]:IEEE,1997:1845-1848. [6] 于華楠,郭樹旭.基于壓縮感知的超寬帶信道估計方法的研究[J].電子與信息學報,2012,34(6):1452-1456. [7] 焦東立,朱立東.一種基于壓縮感知的信道估計算法[J].空間電子技術,2011,8(3):16-19. [8]TaubockG,HlawatschF,EiwenD,etal.Compressiveestimationofdoublyselectivechannelsinmulticarriersystems:leakageeffectsandsparsityenhancingprocessing[J].IEEEJournalofSelectedTopicsinSignalProcessing,2010,4(2):255-271. [9]DoTT,LuG,NguyenN,etal.Sparsityadaptivematchingpursuitalgorithmforpracticalcompressedsensing[C]//Procof2008 42ndAsilomarconferenceonsignals,systemsandcomputers.CA,PacificGrove:[s.n.],2008. [10]ApplebaumL,BajwaWU,CalderbankAR,etal.DeterministicpilotsequencesforsparsechannelestimationinOFDMsystems[C]//Procof2011 17thinternationalconferenceondigitalsignalprocessing.Corfu:[s.n.],2011. [11]SharpM,SacglioneA.Ausefulperformancemetricforcompressedchannelsensing[J].IEEETransactionsonSignalProcessing,2011,59(6):2982-2988. [12]CandesE,TaoT.Nearoptimalsignalrecoveryfromrandomprojections:universalencodingstrategies[J].IEEETransactionsonInformationTheory,2006,52(12):5406-5425. [13] 石光明,劉丹華,高大化,等.壓縮感知理論及其研究進展[J].電子學報,2009,37(5):1070-1081. [14] 戴瓊海,付長軍,季向陽.壓縮感知研究[J].計算機學報,2011,34(3):425-434. Adaptive Pilot Channel Estimation Based on Compressive Sensing SUN Jun,GAO Jie (School of Communication and Information Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China) In wireless communication system,how to improve the accuracy of channel estimation is very important for improvement of the performance for wireless communication system.In the channel estimation,the pilot overhead occupies a large amount of spectrum resources,and the traditional channel estimation algorithm cannot adjust the pilot channel estimation according to the channel state.The compressed sensing channel estimation algorithm,taking advantage of the sparse characteristic of wireless channel,improves the accuracy of channel estimation and decreases the pilot overhead.Based on these features,combined compressive sensing with channel estimation,investigating channel estimation with unknown channel sparsity based on compressive sensing,an adaptive pilot channel estimation algorithm is put forward for LTE-Advanced systems.Simulation shows that compared with the traditional LS and LMMSE,it can reduce the number of pilot by 40% and obtain more accurate channel estimation performance. compressive sensing;channel estimation;adaptive;pilot 2015-12-04 2016-03-09 時間:2016-08-01 國家“863”高技術發展計劃項目(2005AA121620,2006AA01Z232);江蘇省普通高校研究生科研創新計劃資助項目(CX07B_110z);南郵校級項目(NY211033) 孫 君(1980-),女,碩士研究生導師,研究方向為無線通信;高 杰(1989-),男,碩士研究生,研究方向為移動通信與無線通信。 http://www.cnki.net/kcms/detail/61.1450.TP.20160801.0907.048.html TP301 A 1673-629X(2016)10-0184-04 10.3969/j.issn.1673-629X.2016.10.040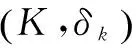


3 導頻自適應的壓縮感知信道估計
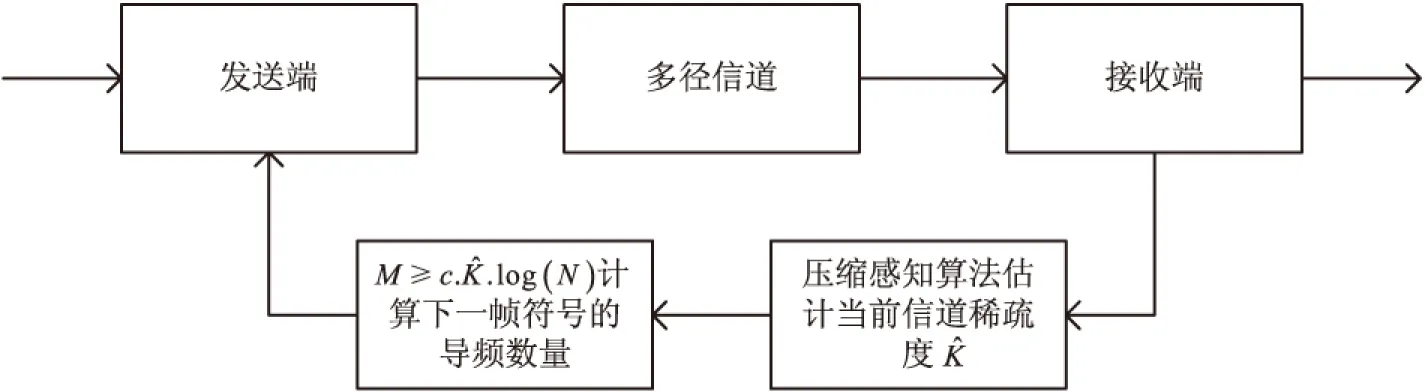
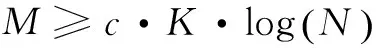
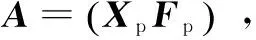

4 仿真結果與分析


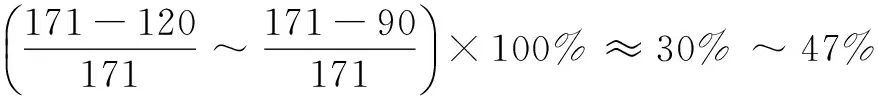
5 結束語

