一種基于亞像素角點的SIFT立體匹配算法研究

洪 磊,嵇保健,洪 峰

(1.南京工程學院 汽車與軌道交通學院,江蘇 南京 211167；2.南京工業大學 自動化與電氣工程學院,江蘇 南京 211800；3.南京航空航天大學 電子信息工程學院,江蘇 南京 210016)

一種基于亞像素角點的SIFT立體匹配算法研究

洪 磊1,嵇保健2,洪 峰3

(1.南京工程學院 汽車與軌道交通學院,江蘇 南京 211167；2.南京工業大學 自動化與電氣工程學院,江蘇 南京 211800；3.南京航空航天大學 電子信息工程學院,江蘇 南京 210016)

針對尺度不變特征變換(SIFT)算法在立體匹配應用中實時性差、誤匹配、特征點無鮮明幾何意義等問題，提出了一種新的基于亞像素角點的SIFT立體匹配算法。該算法首先提取圖像角點作為特征點，并通過擬合內插法精確定位其亞像素坐標。在角點鄰域內利用圖像的梯度信息構造基于梯度直方圖統計信息的特征描述子，最后通過對特征描述子的對稱性相似度測量以及隨機采樣一致性篩選獲得最終的目標匹配點。實驗結果表明，該方法在保持較強魯棒性的基礎上，較大幅度地提高了算法的實時性能和匹配精度。

立體匹配;亞像素角點;尺度不變特征變換;機器視覺

0 引 言

立體匹配是立體視覺技術中的重要組成部分，其本質是通過給定一幅圖像中的一個點，尋找另一幅圖像中的對應點，使得這兩點為空間同一物體點的投影。由于立體視覺技術建立在對應點的視差之上，因而圖像中對應點的匹配關系成為了機器視覺中一個極為重要的難點問題，在機器人視覺、航空測繪、醫學診斷、虛擬現實技術等領域得到了廣泛應用。傳統上，有基于圖像灰度的匹配、基于圖像特征和基于解釋的匹配或者多種方法相結合的立體匹配方法[1]。

由于傳統直接利用局部灰度特征進行相關匹配的方法對噪聲和灰度的非線性變換極為敏感，近年來很多學者對灰度變化梯度、領域灰度統計信息等間接利用圖像灰度值特征的方法進行了廣泛研究[2-4]。其中，Lowe D G提出的SIFT是目前最成功的局部特征提取算子[5]。SIFT以圖像尺度空間極值點為特征點，通過對每個特征點進行精確定位、主方向選擇及灰度梯度直方圖統計生成特征點描述子。研究表明，SIFT特征點定位準確，具有很好的尺度、旋轉、視角和光照不變性，優于其他局部特征提取算子。目前，SIFT已成功應用于目標識別、圖像視頻檢索、全景拼接和視覺定位等領域。不過SIFT提取的特征也存在如下不足[6]：

(1)其特征點不是人們視覺意義上的角點，缺乏鮮明的幾何意義；

(2)SIFT特征計算復雜度高且運算量大，其實時性較差，難以應用于對實時性要求較高的系統；

(3)SIFT特征點數量龐大，增加了特征匹配的時間負擔，增大了誤匹配率，降低了算法運行效率。

針對上述不足，文中提出了一種新的基于亞像素角點的SIFT立體匹配算法。該算法首先提取具有鮮明幾何意義的角點作為特征點，通過擬合內插法精確地定位其亞像素坐標；然后在角點領域內，利用圖像的梯度信息構造基于梯度直方圖統計信息的特征描述子，最后對特征描述子進行對稱性相似度測量，并采用隨機采樣一致性算法進行篩選，以確定最終匹配點。實驗結果表明，該方法提高了匹配精度，降低了算法時間復雜度和誤匹配率，在保持了SIFT算法較強魯棒性的基礎上，彌補了其實時性差、誤匹配、特征點無鮮明幾何意義的缺點，在機器視覺系統中具有一定的實用性。

1 算法原理

1.1 算法框架及流程

對于任何一種立體匹配方法，其有效性依賴于3個問題的解決，即選擇正確的匹配特征、尋找特征間的本質屬性及建立能正確匹配所選特征的穩定算法[7]。從上述三個方面出發，文中建立的算法基本框架如圖1所示。

圖1 算法框架圖

假設工作環境中兩幅圖像拍攝的光照條件相當，若尋找兩幅圖像對應的匹配點，具體實現流程如下：

(1)載入兩幅待匹配的圖像數據；

(2)分別提取兩幅圖像的角點，確定每個角點的亞像素坐標；

(3)對于每個提取的角點，計算其鄰域內的梯度方向直方圖，生成SIFT特征描述子；

(4)通過計算兩幅圖像各角點特征描述子之間的歐氏距離，進行對稱性相似度測量，利用近似最近鄰算法確定初始匹配點對；

(5)以初始匹配點對為樣本集，采用隨機采樣一致性算法進行匹配篩選，剔除誤匹配及冗余匹配之后，確定最終匹配點對。

1.2 基于Harris算子的亞像素角點提取

圖像中的角點具有鮮明的幾何意義，保留了圖像豐富的信息量，易于測量和表示，應用十分廣泛。目前常見的角點檢測算子主要有Moravec算子、Forstner算子、Harris算子和SUSAN算子[8-10]等。其中，Harris算子對攝像機姿態及光照的變化具有較好的穩定性，計算簡單，角點提取可靠性高，非常適合相對復雜背景和光線不均勻性的特點，故文中采用Harris算子進行角點提取。

但是Harris算子的定位性較低，其探測精度是像素級的，而一般來說角點的位置并不恰好位于某像素的正中位置，所以Harris算子僅能得到角點位置的近似值，這對后續計算帶來了誤差。為此文中算法在Harris角點檢測的基礎上，通過對角點子域的像素灰度進行擬合內插，獲取亞像素角點坐標。如圖2所示，其中點C是角點的實際位置。

圖2 角點子域的像素灰度內插

擬合曲面通常采用高斯曲面，其函數為：

(1)

其中，擬合出的(x0,y0)即為角點的內插位置。

由于高斯函數具有可分離的性質，因此有：

(2)

利用式(2)使二維高斯曲面擬合由兩個一維高斯曲面擬合來完成，簡化了擬合過程。通過高斯曲面擬合內插后的角點探測精度為亞像素級，在算法編程上，可利用OpenCV提供的cvGoodFeaturesToTrack和cvFindCornerSubPix函數來實現[11]。

1.3 特征描述子的生成

特征描述子的生成首先建立在特征提取的基礎上。SIFT特征點在實際應用中由于缺乏直觀幾何意義,存在一定的局限性。為彌補這一不足，文中采用角點代替SIFT原有的特征點，以角點周圍的圖像梯度變化信息，構造基于三維梯度方向直方圖的區域性特征描述子，見圖3。

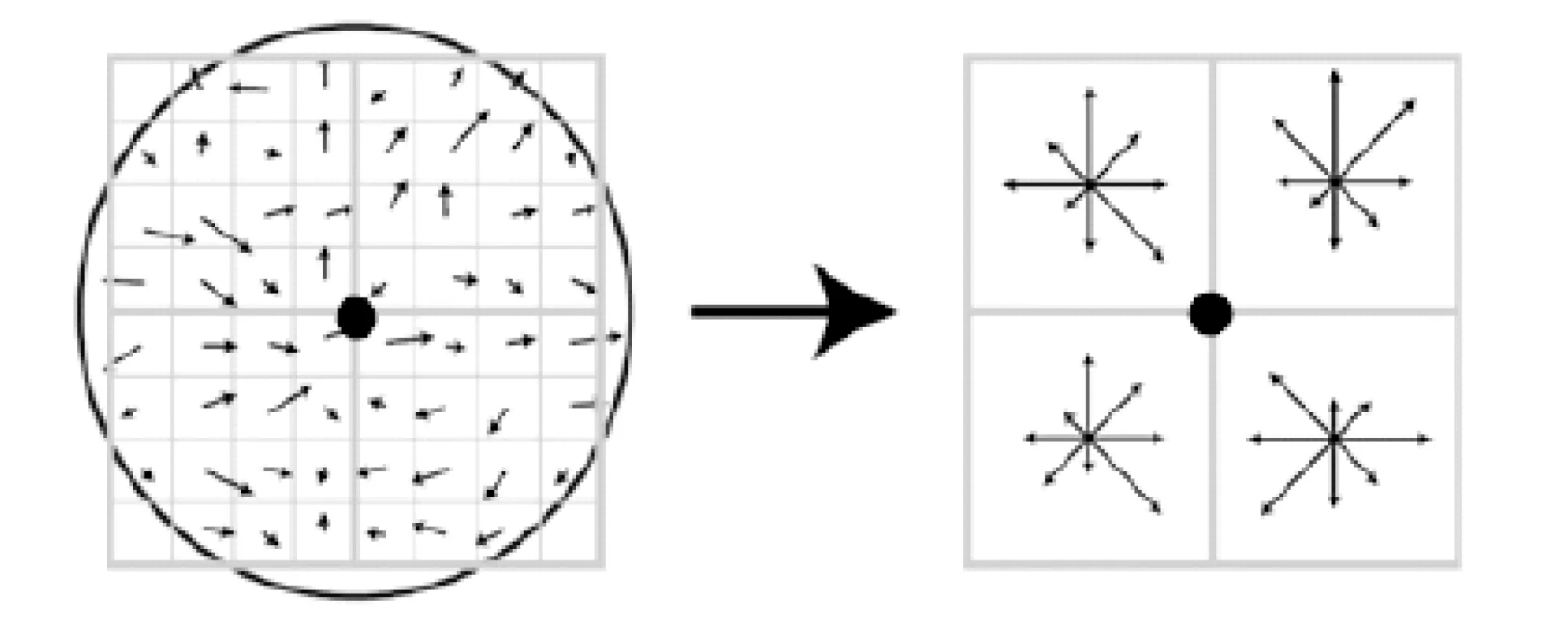
圖3 由角點領域梯度信息生成特征描述子

具體生成方法如下：

(1)如圖3所示，以角點為原點，沿圖像x,y軸方向建立初始主坐標系，計算角點的梯度方向作為主方向。

(2)以角點為中心，選取大小為8×8的窗口，其中每個小窗口含3×3個像素。首先將初始主坐標系x軸旋轉至與描述子主方向重合位置，得到實際主坐標系以獲得旋轉不變性，然后計算每個小窗口中心像素的梯度加權幅值與方向，公式如下：

m(x,y)=[(f(x+1,y)-f(x-1,y))2+ (f(x,y+1)-f(x,y-1))2]1/2

θ(x,y)=tan-1((f(x,y+1)-f(x,y-1))/ (f(x+1,y)-f(x-1,y)))

(3)

(3)以特征角點為中心，分別對左上、右上、左下、右下四個4×4窗口區域中的每個原子窗口中心像素計算其相對于主坐標系x軸的梯度方向，并通過近似判定將其分類到八個方向之一(如圖3右所示)，最后依據其加權幅值的大小在每個方向上進行累加統計出其直方圖。

(4)按左上、右上、左下、右下的順序，以相對于每個4×4窗口中心點的八個方向的向量統計長度生成2×2×8即32維特征向量，將其進行歸一化處理以消除光照不均勻的影響，最終得到特征描述子。Lowe指出，當以特征點為中心選取16×16窗口，也即形成4×4×8=128維特征向量時，該特征描述子擁有最佳匹配特性。文中為降低算法的時間復雜度，采用32維特征向量。

1.4 基于近似最近鄰算法的特征匹配

當兩幅圖像特征點的特征描述子向量生成后，需進行特征點匹配，設圖像1和2的第i個特征點描述子分別為:Ri=(ri1,ri2,…,ri32),Si=(si1,si2,…,si16)。

采用特征描述子向量之間的歐氏距離作為兩幅圖像中特征點的相似性判定度量，即：

(4)

要得到配對的特征點描述子(Ri,Si)，這里采用最近鄰和次近鄰特征點距離之比來減小誤匹配的情況。即滿足式(5)：

(5)

降低比例閾值Threshold，特征點的匹配點數目會減少，但穩定性更強。在文中實驗，最近鄰特征點距離與次近鄰特征點距離之比取0.5。

對于最鄰近及次鄰近的特征點的搜索，最簡單的方法是采用線性掃描，即窮舉法，但由于特征點數量較大，故窮舉法的時間復雜度很大，不適合實時應用。JonLouisBentley提出了Kd樹搜索算法[12]，該方法將待查詢特征點集構造為稱作Kd樹的數據結構，并提供了一種類似二叉樹查詢的高效搜索機制，從而大大降低了尋找最佳匹配的計算量。Kd樹法在空間維數K較低時效率非常高，但對于K較大(K>10)時,其執行效率較低。此時Kd樹法表現出較差的搜索效率，基本等同于窮舉法，因此亦不實用。

針對Kd樹算法的不足，文中采用近似最近鄰算法即BBF(Best-Bin-First)算法[13]。該方法是對Kd樹算法的改進，它采用一個優先級隊列優化了Kd樹對其節點的搜索順序，并限定了搜索的最大次數，從而能快速地找到最近鄰和次近鄰點。由于文中采用的SIFT特征描述子具有32維，屬于高維度空間，因此采用BBF算法提高了搜索效率，降低了時間復雜度。

1.5 基于隨機采樣一致性算法的匹配篩選

對于上述基于亞像素角點提取的SIFT特征，再用BBF搜索算法進行候選匹配，此時仍然還存在比較多的錯誤和冗余匹配點，故文中采用隨機采樣一致性算法對候選匹配對進行篩選。

隨機采樣一致性算法，即RANSAC(RANdom SAmple Consensus)算法，是一種魯棒的變換估計算法。它利用特征集合的內在幾何約束關系進一步剔除錯誤的匹配[14]，其在SIFT特征篩選中的主要流程為：

(1)從候選匹配特征點樣本集中隨機抽選一個RANSAC樣本，即n個匹配點對，實驗中取n=4；

(2)根據這n個匹配點對計算兩幅圖像之間的變換矩陣H；

(3)根據特征點樣本集、變換矩陣H和誤差度量函數計算滿足當前變換矩陣的一致集，并返回一致集中元素個數；

(4)根據當前一致集中元素個數判斷是否最優(最大)一致集，若是則更新當前最優一致集;

(5)更新當前錯誤概率P，公式為：

P=(1-in_fracm)k

(6)

其中,in_frac是當前最優一致集中元素個數占樣本總數的百分比；m是計算變換矩陣需要的最小特征點對個數，實驗中取m=4；k是迭代次數。

若P大于允許的最小錯誤概率Pmin，則重復(1)至(4)繼續迭代，直到當前錯誤概率P小于Pmin，實驗中取Pmin=0.01，使匹配正確率達到99%。

2 實驗研究

為測試文中所述匹配算法的實際應用性能，進行了專項實驗進行驗證。實驗所采用的雙目立體視覺系統包括2臺1/3英寸SONYXC-ES50CECCD工業攝像機，2臺ComputarM0814-MP2 8mm焦距鏡頭和大恒DHCG410圖像采集卡。實驗所采集的圖像是一張8×8的正方形的棋盤格平面圖樣，其中每個正方形的尺寸為20mm×20mm。以下是對算法的實驗驗證與分析。

2.1 實驗1：實時性與誤匹配率分析

實驗1的結果如圖4(a)～(d)所示。

圖4 實驗1的匹配結果比較

其中，圖4(a)和(b)給出了未經匹配篩選之前原SIFT算法與文中算法的匹配結果。其算法耗時、匹配正確率如表1所示。

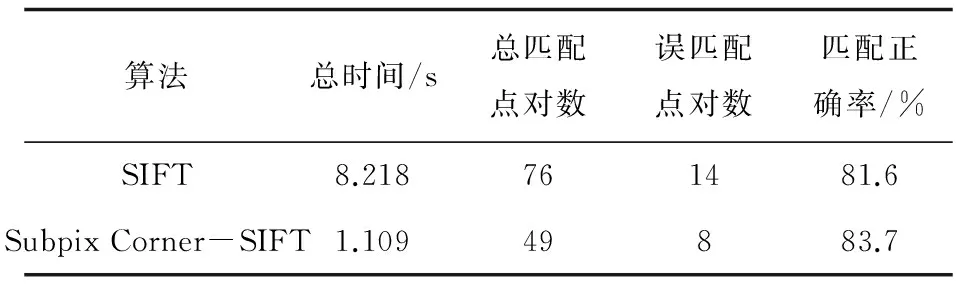
表1 SIFT算法與文中算法的比較(未篩選前)

由表1的結果表明，文中算法所得到的匹配點數量比原SIFT算法有所減少，耗時大大降低，從而節約了算法的匹配時間，加快了算法的匹配速度。匹配正確率都超過了80%，證明了算法的魯棒性，但在未經過RANSAC算法篩選之前，仍有一定的錯誤匹配點對的存在。

篩選后的匹配圖像如圖4(c)和(d)所示，匹配點對數有所減少，如表2所示。

表2 RANSAC算法的篩選

由此可見，RANSAC篩選降低了誤匹配率，使匹配結果更加精確。

2.2 實驗2：精度分析

文中算法在Harris角點提取的基礎上采用內插法將角點位置精度精確到亞像素級，以下通過棋盤格上的P1～P4(見圖5)間的距離測試對算法精度進行分析。

圖5 P1～P4的匹配

表3給出了測定的P1～P4在左、右攝像機的圖像坐標；表4給出了距離測試結果。

從表4給出的距離測試結果可知,亞像素級角點提取進一步提高了匹配點對的位置精度，從而提高了整個算法精度，有利于在雙目視覺系統中的實際應用。

表3 P1～P4在左、右攝像機的圖像坐標

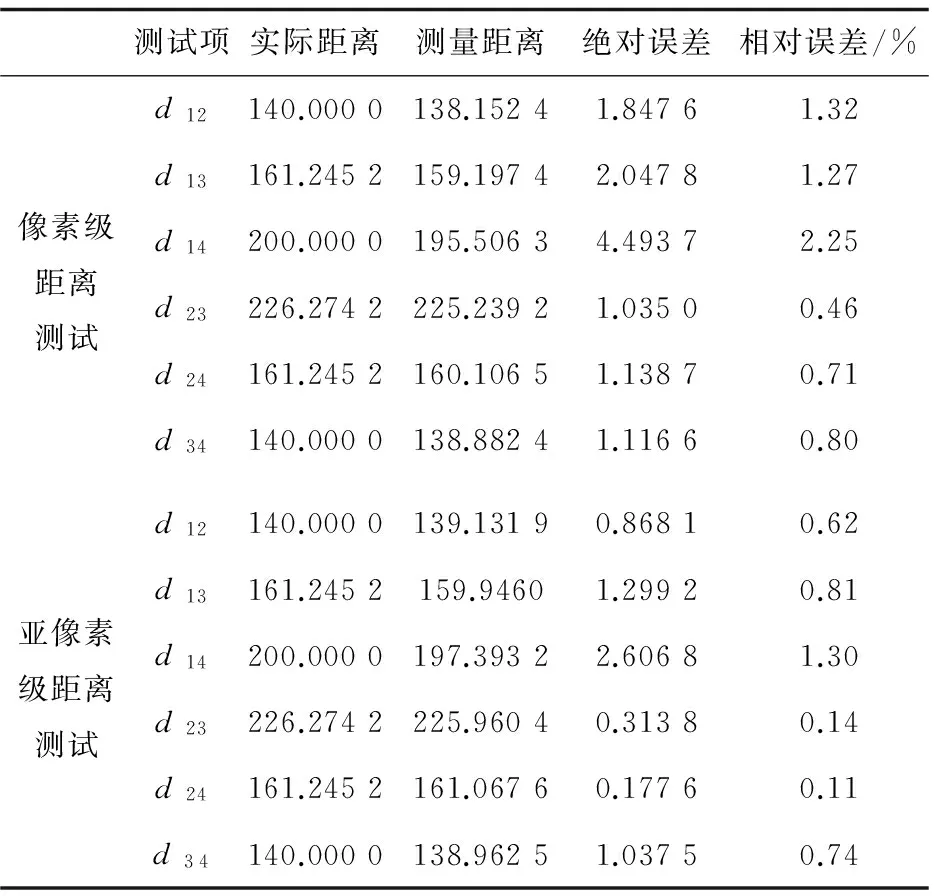
表4 像素級與亞像素級距離測試結果比較 mm

3 結束語

SIFT算法具有很好的尺度、旋轉、視角和光照不變性，優于其他局部特征提取算子，但當應用于對實時性要求較高的雙目視覺立體匹配時，該算法的復雜度較高、實時性較差，且其特征點不具備鮮明的幾何特征，使算法的尺度不變特性優勢難以體現出來。文中提出的基于亞像素角點的SIFT算法是對SIFT的一個成功改進，在保證SIFT算法魯棒性的基礎上，提高了匹配精度，降低了特征提取和特征匹配的復雜度，大大提高了算法的實時性。通過雙目立體視覺匹配實驗的結果驗證了文中算法的有效性和實用性。

[1] 張廣軍.機器視覺[M].北京:科學出版社,2005.

[2] 高曉峰,史朝輝.一種改進的基于灰度投影的圖像匹配算法[J].航空計算技術,2012,42(6):85-87.

[3] 曾 凱,王慧婷.基于區域灰度增強的種子特征匹配方法[J].中國農業大學學報,2013,18(5):136-140.

[4] 唐 爍,繆 源.基于Harris角點的圖像匹配算法[J].微型機與應用,2013,32(2):41-43.

[5]LoweDG.Distinctiveimagefeaturefromscale-invariantkeypoints[J].InternationalJournalofComputerVision,2004,9(6):35-51.

[6] 齊乃新,曹立佳,楊小岡,等.基于方向約束的改進SIFT匹配算法[J].計算機科學,2014,41(6A):125-128.

[7] 趙欽君,趙東標,韋 虎.Harris-SIFT算法及其在雙目立體視覺中的應用[J].電子科技大學學報,2010,39(4):546-550.

[8] 丁雄飛,張春燕.基于Moravec算子和改進的SIFT算法的圖像匹配[J].合肥學院學報：自然科學版，2013,23(3):40-42.

[9] 龍忠杰,王吉芳,左云波.一種改進的Harris與SUSAN相結合的角點檢測算法[J].計算機應用與軟件,2013,30(12):133-136.

[10] 樊志華,王春鴻,饒長輝,等.基于Harris角點量與相位相關的亞像素級圖像配準方法[J].計算機應用研究,2011,28(2):788-791.

[11] 布拉德斯基.學習OpenCV[M].北京:清華大學出版社,2009:353-355.

[12] 丁南南,劉艷瀅,張 葉,等.基于SURF-DAISY算法和隨機kd樹的快速圖像配準[J].光電子·激光,2012,23(7):1395-1402.

[13] 陳小丹,杜宇人,高秀斌.一種基于SURF的圖像特征點快速匹配算法[J].揚州大學學報:自然科學版,2012,15(4):64-67.

[14] 王任華,霍宏濤,蔣 敏.RANSAC算法在同圖復制鑒定中的應用研究[J].計算機應用研究,2014,31(7):2209-2212.

Research on a SIFT Stereo Matching Algorithm Based on Sub-pixel Corners

HONG Lei1,JI Bao-jian2,HONG Feng3

(1.School of Automotive and Rail Transit,Nanjing Institute of Technology,Nanjing 211167,China;2.College of Automation and Electrical Engineering,Nanjing University of Technology,Nanjing 211800,China;3.College of Electronic and Information Engineering,Nanjing University of Aeronautics &Astronautics,Nanjing 210016,China)

In view of the problems of the poor real-time performance,mismatching and no distinct geometric characteristics points on stereo matching application based on the Scale Invariant Feature Transform (SIFT) algorithm,present a new SIFT stereo matching algorithm based on sub-pixel corners.At first,the image corners are extracted and located in sub pixel coordinates by fitting interpolation method.Then the feature descriptors are established by the field gradient image histogram information structure based on the statistical information for the corners.Finally,the symmetrical characteristic similarity is measured and random sample consensus algorithm is used to achieve ultimate matching points.Experiments show that the proposed algorithm based on strong robustness,can greatly improve the real-time performance and the matching precision.

stereo matching;sub-pixel corner;SIFT;machine vision

2015-03-29

2015-07-01

時間：2015-11-19

江蘇省產學研聯合創新資金研究項目(BY2014005-09)；南京工程學院科研基金項目(YKJ201333)

洪 磊(1982-),男,博士,講師,研究方向為機器視覺技術、軌道車輛微機控制技術。

http://www.cnki.net/kcms/detail/61.1450.TP.20151119.1113.074.html

TP391.41

A

1673-629X(2016)01-0048-05

10.3969/j.issn.1673-629X.2016.01.010