Hilbert空間上多集合分裂可行問題的KM迭代算法

羅 俊,劉 健

(1．南京郵電大學 理學院，江蘇 南京 210023；2．南京郵電大學 通信與信息工程學院，江蘇 南京 210003)

Hilbert空間上多集合分裂可行問題的KM迭代算法

羅 俊1,劉 健2

(1．南京郵電大學 理學院，江蘇 南京 210023；2．南京郵電大學 通信與信息工程學院，江蘇 南京 210003)

多集合分裂可行問題就是尋找與一族非空閉凸集距離最近的點，并使得該點在線性變換下的像與另一族非空閉凸集的距離最近。分裂可行問題是一類重要的最優化問題，產生于工程實踐，在醫學、信號處理和圖像重建等領域中有著廣泛的應用。文中基于n維線性空間上求解分裂可行問題的KM迭代算法，目的是要將算法在Hilbert空間中加以推廣應用。通過在Hilbert空間中運用投影壓縮定理，并且利用逼近函數將多集合分裂可行問題轉化為最小值問題，方便了對算法的推導證明。利用上述方法可得，多集合分裂可行問題的KM迭代算法在Hilbert空間中也有較好的收斂性。因此，可以將多集合分裂可行問題的KM迭代算法在Hilbert空間中加以推廣。

多集合分裂可行問題；優化問題；KM迭代；Hilbert空間

1 概 述

分裂可行問題(Split Feasibility Problem,SFP)是一類非常重要的約束優化問題，它最早出現在Censor和Elfving(1994)的文獻[1]中，定義如下：

設A是實矩陣且A∈Rm×n，C,Q分別是Rn,Rm中的非空閉凸子集，分裂可行問題就是要尋找這樣的元素x(如果這樣的元素x是存在的),使得x∈C,Ax∈Q。

多集合分裂可行問題(Multiple-SetsSplitFeasibilityProblem,MSSFP)是SFP的推廣，是很多問題的反問題的數學模型。MSSFP是這樣一個問題：

多集合分裂可行問題產生于工程實踐，是一類重要的最優化問題，在醫學[3]、信號處理[2]和圖像重建[4]等領域中有著廣泛的應用。MSSFP是SFP的推廣與泛化，XuHongkun在文獻[2]中最早提出了MSSFP。已經有不少人對MSSFP的求解算法進行了研究，也取得了一定的進展。Censor等在文獻[3-4]中給出了一種求解MSSFP的投影算法：

定義逼近函數:

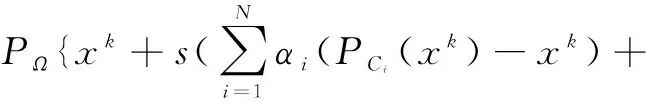
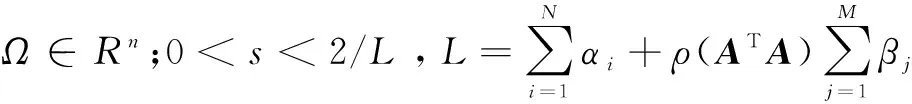
隨著人們對分裂可行問題研究的深入，衍生了一系列反問題，定義如下：

設C,Q分別是Rn,Rm中的非空閉凸子集，A是Rm×n中實矩陣，A+是A的Moore-Penrose廣義逆。SFP的反問題ISFP形如：尋找元素y(如果這樣的y存在)：

y∈Q,A+y∈C

根據SFP與ISFP的對偶性，可以通過研究SFP的求解算法進而研究ISFP的求解。楊慶之[5]給出了一種ISFP問題的求解算法，迭代格式如下：

在此基礎上，王新艷和屈彪[6]給出了下列推廣形式：

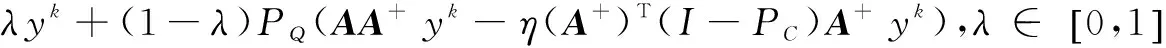
推廣之后的算法在迭代點的選取上具有更大的靈活性與更多的選擇性。

后來，在前人的基礎之上，Krasnoselski-Mann提出了形如式(1)的迭代格式稱為KM迭代[7]。

xk+1=(1-ηk)xk+ηkN(xk),k=0,1,…

(1)

其中，N是Rn中的非擴張算子；ηk∈(0,1)，特別地，當N是強制非擴張算子時[8]，ηk∈(0,2)。

KM迭代的目標是尋找算子N的不動點，許多領域的很多問題及反問題都可以歸結為尋找某個算子N的不動點[9]。雖然KM迭代格式簡單，但是它在求非擴張算子N的不動點時效果非常顯著，并且為許多領域的算法提供了一個統一的框架。在文獻[5]中，給出了Rn空間中的一些算法。為了擴展算法的適用范圍，而不僅僅局限于Rn空間，現在希望將其中的某些算法在Hilbert空間中加以推廣利用。

2 預備知識

定義1[10]：假設X為帶有內積〈·,·〉和范數‖·‖的Hilbert空間，對給定的Ω∈X,v∈X,如下問題：

min{‖u-v‖|u∈Ω}

的解稱之為v在Ω上的投影,記作PΩ(v)。可以寫成：

PΩ(v)=arg min{‖u-v‖|u∈Ω}

若Ω是閉凸集，則對?v∈X,PΩ(v)是唯一存在的。

定義2[10]：設Ω是非空閉凸集，X1,X2為Hilbert空間；F是Ω?X1到X2的映射。

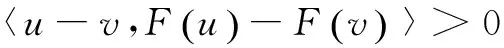
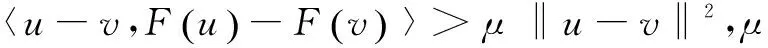
(4)如果存在常數λ>0，使得‖F(u)-F(v)‖≤λ‖u-v‖,?u,v∈Ω，那么稱F在Ω上是Lipschitz連續的，特別地，λ=1時，稱F為非擴張算子；

定義3[10]：

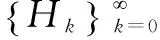
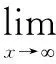
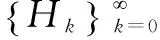
(2)給定?ρ≥0，Hilbert空間中算子H1,H2的ρ-距離定義為：

Dρ(H1,H2)=

(2)

(3)設C1,C2是Hilbert空間中非空閉凸子集，C1,C2之間的ρ-距離定義為：

dρ(C1,C2)=

(3)

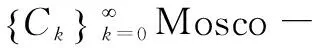
投影的性質有以下定理：

定理1[12]：若Ω是Hilbert空間X中的非空閉凸集，則有：

證明：根據投影定義得到

‖v-PΩ(v)‖2≤‖v-w‖2,?w∈Ω

因為Ω?X是非空閉凸集，則對于?u∈Ω，0<σ<1有：

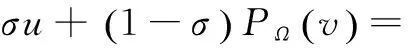
整理后得：

令σ→0+，得：

證畢。

定理2[11-12]：若Ω?X是非空閉凸集，?v,u∈X,z∈Ω則有：

下面介紹收斂性分析中需要用到的KM定理。

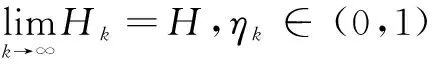
xk+1=(1-ηk)xk+ηkHk(xk)

(4)

3 算法及其證明

對于多集合分裂可行問題，首先作下面的假設：

(H1)MSSFP的解集非空；

(H3)對?x∈X1，至少存在一個次梯度ξ∈?ci(x)，其中

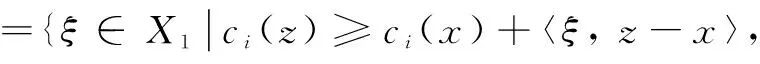
對?y∈X2，至少存在一個次梯度η∈?qj(y)，其中

為了求解MSSFP，定義逼近函數：

那么尋找MSSFP的一個解，就可以轉化為求解如下最小值問題：

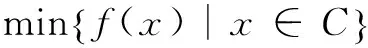
Censor等提出了以下的迭代公式：

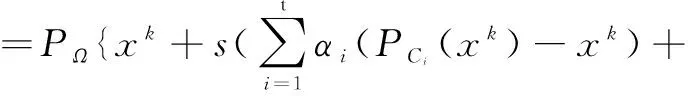
后來又有研究者對單集合分裂可行問題的CQ算法進行了改進，令上述迭代公式中s=αk=βγmk,其中β,γ是給定的常數，且滿足β>0,γ∈(0,1)，mk是使下列不等式：

f(xk+1)≤f(xk)-σ

成立的最小非負整數，常數σ∈(0,1)。

將算法將推廣到多集合分裂可行問題，在已有算法的基礎上，利用KM迭代得到一種自適應不精確算法1。

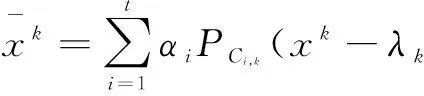
(5)

其中，λk=γlmk,mk是使下式成立的最小非負整數。

(6)

令

(7)

(8)

定義算子：

(9)

(10)

由于正交投影PCi,k是強制非擴張算子，于是有：

‖Hkx-Hky‖2

所以，Hk是強制非擴張算子。同理，H也是強制非擴張算子。

由式(8)知式(7)可以寫成：

xk+1=(1-ηk)xk+ηkHk(xk)

(11)

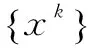
(12)

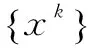
證明：記

(13)

(14)

對?x∈H，‖x‖≤ρ，ρ>0有

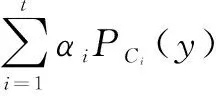
(15)

由于正交投影是非擴張的，所以

‖yk-y‖

(16)

將式(13)、(14)代入式(15)再結合式(16)得到:

‖Hk(xk)-H(xk)‖≤

(17)

根據對任意有界線性算子B[14]，有‖Bx‖≤‖B‖‖x‖，可以得到：

‖Hk(xk)-H(xk)‖≤

由式(2)和式(3)得到：

(18)

4 結束語

多集合分裂可行問題在現實中的許多領域有著廣泛的應用。到目前為止，多集合分裂可行問題的許多算法的求解都是在Rn空間中完成的，而在Hilbert空間中的推廣應用還有待完善。文中基于Rn空間中求解多集合分裂可行問題的KM迭代算法，給出了Hilbert空間中的一種自適應不精確算法，以及算法的收斂性證明。

[1]CensorY,ElfvingT.Amulti-projectionalgorithmusingBregmanprojectionsinaproductspace[J].NumberAlgorithms,1994,8:221-239.

[2]XuHongkun.AvariableKrasnosel’ski-Mannalgorithmandthemultiple-setsplitfeasibilityproblem[J].InverseProblems,2006,22:2021-2034.

[3]CensorY.Row-actionmethodsforhugeandsparsesystemsandtheirapplications[J].SIAMReview,1981,23(4):444-466.

[4]CensorY,BortfeldT,MartinB,etal.Unifiedapproachforinversionproblemsinintensity-modulatedradiationtherapy[J].PhysicsinMedicineandBiology,2006,51:2353-2365.

[5] 楊慶之,趙金玲.分裂可行問題(SFP)的投影算法[J].計算數學,2006,28(2):121-132.

[6] 王新艷,屈 彪.求解分裂可行問題逆問題的算法推廣[J].泰山學院學報,2010(6)：10-14.

[7]ZhaoJinling,YangQingzhi.AnoteontheKrasnoselski-Manntheoremanditsgeneralizations[J].InverseProblems,2007,23:1011-1016.

[8]CensorY,MotovaA,SegalA.Perturbedprojectionsandsubgradientprojectionsforthemultiple-setssplitfeasibilityproblem[J].JournalofMathematicalAnalysisandApplications,2007,327(2):1244-1256.

[9]BauschkeHH,BorweinJM.Onprojectionalgorithmsforsolvingconvexfeasibilityproblems[J].SIAMReview,1996,38:367-426.

[10]EickeB.Iterationmethodsforconvexlyconstrainedill-posedproblemsinHilbertspace[J].NumericalFunctionalAnalysisandOptimization,1992,13(5-6):413-429.

[11]WangC,XiuN.Convergenceofthegradientprojectionmethodforgeneralizedconvexminimization[J].ComputationalOptimizationandApplications,2000,16(2):111-120.

[12]ZarantonelloEH.ProjectionsonconvexsetsinHilbertspaceandspectraltheory[D].Wisconsin:UniversityofWisconsin,1971.

[13] 何炳生.論求解單調變分不等式的一些投影收縮算法[J].計算數學,1996(1):97-103.

[14] 徐成賢，陳志平，李乃成.近代優化方法[M].北京: 科學出版社,2002:18-35.

KM Iterative Algorithm for Multiple-sets Split Feasibility Problem in Hilbert Space

LUO Jun1，LIU Jian2

(1.College of Science,Nanjing University of Posts & Telecommunications,Nanjing 210023,China;2.College of Communication and Information Engineering,Nanjing University of Posts &Telecommunications,Nanjing 210003,China)

The multiple-sets spilt feasibility problem requires finding a point closest to a family of closed convex sets in one space,so that its image under a linear transformation will be closest to another family of closed convex sets in the image space.The multiple-sets spilt feasibility problem is an important type of optimization problem,which is generated from engineering practice and already has been widely applied in medical science,signal processing,image reconstruction.Based on KM iterative methods for solving the multiple-sets spilt feasibility problem in Rn space,try to spread this algorithm in Hilbert Space.Using projection compression theorem and approximation function transformed the multiple-sets spilt feasibility problem into a minimum value problem,making the algorithm proving more easily.By deducing and proving,the multiple-sets spilt feasibility problem has good convergence in Hilbert Space.So the result shows that the KM iterative methods are spread in Hilbert Space perfectly.

multiple-sets split-feasibility problem;optimization problem;KM iteration;Hilbert Space

2015-04-22

2015-07-23

時間：2016-01-04

國家自然科學基金面上項目(61070234)

羅 俊(1989-)，男，碩士研究生，研究方向為數值方法與應用。

http://www.cnki.net/kcms/detail/61.1450.TP.20160104.1505.036.html

TP

A

1673-629X(2016)01-0043-05

10.3969/j.issn.1673-629X.2016.01.009