降落傘附加質量的計算方法

黃偉

（1 國防科學技術大學，長沙 410073）

（2 北京空間機電研究所，北京 100094）

降落傘附加質量的計算方法

黃偉1,2

（1 國防科學技術大學，長沙 410073）

（2 北京空間機電研究所，北京 100094）

降落傘開傘充氣過程中，傘衣的載荷是一個重要的參數。傘衣載荷的計算主要利用傘衣阻力特征變化和附加質量方法，建立起物傘系統動力學方程，求解出開傘充氣過程的載荷變化。因此，附加質量計算的精確程度直接影響了整個開傘載荷的準確性。過去對于附加質量的研究是基于理想傘衣形狀假設下，采用附加質量系數的計算方法，但并未開展附加質量系數的具體確定方法研究。文章對降落傘附加質量進行了研究，包括對降落傘附加質量的概念進行了說明，對降落傘附加質量的數值計算方法進行了初步的探討，重點介紹了當前國際上常用的工程計算方法，包括內含質量計算法、充氣半徑計算法等。通過對不同工程計算方法進行比較分析，得出充氣半徑計算法可計算徑向附加質量和軸向附加質量，對于設計人員而言具備較好的應用價值。

降落傘 氣動減速 附加質量 返回技術

0 引言

降落傘是一種氣動減速裝置，依靠其結構形狀和性能特征來增大所連接物體的氣動阻力，廣泛應用于各種飛行器的氣動減速和穩定，以及人員的安全救生和航空運動。降落傘工作原理雖然簡單，但對其涉及到的工作過程進行分析卻并非易事。例如，降落傘的充氣是一個短時發生的復雜物理過程，降落傘外形、氣動力、質量特性和附加質量等發生急劇的變化，急劇變化的流場和柔性傘衣交互出現“流固”耦合的復雜情況。

由于降落傘工作過程的復雜性，難以準確對其實現理論建模與仿真分析，降落傘設計往往需要開展大量的風洞試驗、空投試驗才能確定并驗證其最終的技術狀態。數十年來，為了提高對降落傘工作過程的分析精度，盡量減少試驗次數，降低研制成本，國內外學者們對降落傘的拉直、充氣及穩降過程的動力學問題開展了大量的研究工作。為了對降落傘動力學問題獲得滿意的分析結果，降落傘附加質量的確定非常重要。美國在“獵戶座”飛船降落傘研制過程中，正開展降落傘附加質量的專題研究，通過理論建模與試驗相結合，力圖提高對降落傘附加質量的計算精度，從而保證對整個降落傘系統工作過程關鍵性能參數仿真分析的可信度[1]。我國多年來對降落傘附加質量的問題也進行了相應的研究，但在降落傘動力學分析中往往對附加質量是基于理想形狀假設下采用附加質量系數的計算方法處理，至于如何確定附加質量的系數卻很少提及。針對此問題，本文對降落傘附加質量進行探討，主要是對國內外用于降落傘附加質量的計算方法進行了歸納和比較，并提出相應的建議，供科研人員參考。

1 降落傘附加質量的概念

物體受外力作用下，在理想流體中作變速運動時會受到慣性阻力的作用，將慣性阻力以動量形式表示則好像是增加了物體所干擾的流體質量一樣，這部分質量稱為附加質量[2]。

附加質量是一個廣義的概念，不僅包括平動質量項，還包括轉動慣量項，以及平動與轉動的耦合項。附加質量和附加質量慣性矩是個矢量，在六自由度運動方程中，附加質量和附加質量慣性矩共有36個分量，如下附加質量矩陣所示。

式中 Mf為附加質量矩陣；λij為附加質量分量，（i，j=1～6）。

對于軸對稱的降落傘而言，附加質量項只存在 λ11、λ22、λ33、λ55、λ66，前三項是質量量綱，它們代表的是線速度的影響，與坐標方向有關；后兩項是慣性矩量綱，代表的是角速度的影響，與坐標方向和坐標原點在物體上的位置有關；且質量項中λ22、λ33相等，慣性矩項中λ55、λ66相等[3]。

對于降落傘而言，尤其是開傘充氣過程，加速度和尺寸相對較大，在開傘載荷的計算中必須考慮附加質量的影響。對于彈道式下降的物傘系統，降落傘的作用力可表達為：

式中 Fs指降落傘的作用力；ρ為空氣密度；V為系統速度；Cx指降落傘阻力系數；A指參考面積；MV、Mp、MA分別指飛行器質量、降落傘質量和附加質量；WV是飛行器重力；t為時間；θ是彈道傾角[4]。

從上式可以看出，附加質量對降落傘作用力有明顯影響，尤其是在充氣、解除收口等運動發生明顯變化的過程中。因此，明確附加質量的確定方法，對于降落傘設計及應用具有重要的意義。

2 降落傘附加質量的數值計算方法

基于流體運動定律的推導，各附加質量的項可由式（3）確定：

式中 φ為流場的速度勢函數；n指表面積的單位外法向矢量；S為物體外表面積[5]。可見，計算附加質量的關鍵就是計算勢函數以及確定物體的形狀。

采用基于邊界元法的數值計算方法來求解降落傘附加質量。邊界元法是以物體邊界積分為基礎的，將邊界面離散化，即將物面邊界劃分單元，根據物理問題的性質在每個單元上分布強度待定的基本解（像源、匯、偶極子等等），這些基本解沿物面的積分為勢函數。為了確定分布強度，可在物面上選取適當的“控制點”，使勢函數在控制點上滿足繞流條件，從而得到確定未知基本解強度的代數方程[6]。

假設降落傘工作時其周邊空氣為不可壓縮氣體，速度勢在流場中滿足拉普拉斯方程，其有控制方程：

邊界條件：

計算時，將降落傘傘衣表面劃分為N個單元，每個單元上布置等強度的源并設置控制點，則每個控制點的速度勢 （ ）φX0可以表示為：

式中 qk指源強； G(X0,X )是格林函數；k為單元序號（k=1，2，…，N），N為單元數量。

即每個控制點上的速度勢和速度可通過所有源影響的疊加得到，結合控制方程和邊界條件，就可以得到關于各個單元源強的線性代數方程組。求解這個方程組后，可以進一步得出流場內任意一點的速度勢和速度，最終利用式（7）得到降落傘的附加質量。

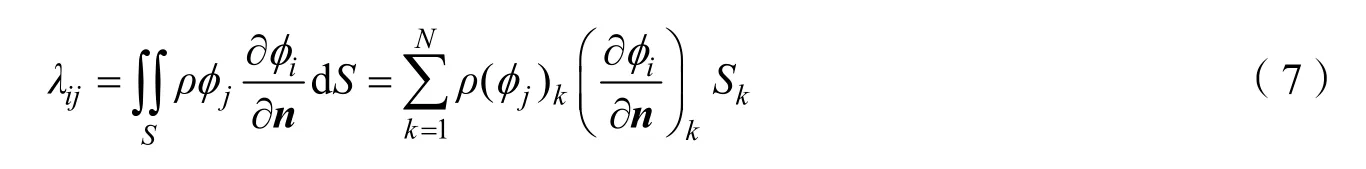
隨著計算流體力學的發展，相應的CFD軟件功能日益強大，利用CFD軟件比基于經典勢流理論推導建模并編程解算更易實現，具備更好的應用前景。利用CFD軟件計算物體的附加質量的基本思路是：對物體及所處的流場進行建模，劃分網格，設置邊界條件；計算時，物體在流場中按照設定的運動規律做非定常運動，并計算得到流體對物體的作用力及力矩，通過對物體受力的分析，從中推算出物體的附加質量。而為了模擬物體的變速運動，可采用動網格方案來適應求解區域相對于慣性坐標系的運動[7]，或是通過對動量方程添加源項以保證流場壓力分布的真實性[8]。文獻[9]對某型平面圓傘的充氣過程利用CFD軟件進行了附加質量的計算，降落傘的形狀是根據試驗照片確定的，按照充氣過程的先后選擇了8張圖片來表征，即為了計算該型平面圓傘充氣過程附加質量的變化，建立了8個不同形狀的降落傘傘衣模型，如圖1所示，并對每個模型按照以上思路分別進行計算。

圖1 某平面圓傘充氣過程的8個不同形狀的傘衣模型Fig.1 Canopy model at eight instants during inflation of a round parachute

綜上所述，無論是采用邊界元法建模求解，還是利用CFD軟件計算降落傘附加質量，均需要明確降落傘的瞬時形狀。

對于降落傘設計及工程應用而言，主要對充氣階段的附加質量需要關注。降落傘進入穩降后由于系統速度的變化平緩，附加質量對系統運動及載荷的影響已經很小。降落傘充氣展開過程傘衣的形狀非常復雜，且變化劇烈，并受到風場、載荷運動變化等多種因素的影響。為了準確計算其附加質量，按照上述的數值計算方法，還需要獲取準確的降落傘充氣過程的形狀變化。為了獲取降落傘充氣過程的形狀變化，還應結合計算流體和流固耦合仿真分析方法確定，或者通過在風洞試驗、空投試驗過程中所拍攝的圖像基礎上進行參數識別。

3 工程計算方法

由于降落傘附加質量的數值計算非常復雜，一般還是采用工程計算方法來解決。國內外學者大多是結合降落傘充氣過程的特點提出相應的工程計算方法，包括阻力面積計算法、內含質量計算法以及充氣半徑計算法等。

3.1 阻力面積計算法

阻力面積計算法認為某一時刻降落傘的附加質量可由阻力面積決定[10]：

3.2 內含質量計算法

內含質量計算法的特點是關注降落傘內部所包含的空氣質量及其產生的表觀質量。認為降落傘附加質量可由兩部分疊加而成，包括內含質量及表觀質量。其中內含質量指某一時刻傘衣內包含的空氣質量，表觀質量指按照勢流理論計算的附加質量[11]。

降落傘附加質量的計算為：

式中 Min指降落傘的內含質量；Map指表觀質量。

該方法中，內含質量由空氣密度和某一時刻的傘衣形狀確定。基于勢流理論，表觀質量亦由傘衣形狀確定。

對于軸對稱的降落傘，在充氣期間，可將傘衣的形狀假定為呈半球形再加一段截錐形的理想形狀，根據參考文獻[2]，充氣過程中的內含質量可按式（10）計算，表觀質量可按式（11）計算。式（11）中，表觀質量實際上是基于該時刻與降落傘同體積的橢球體勢流理論的計算結果。

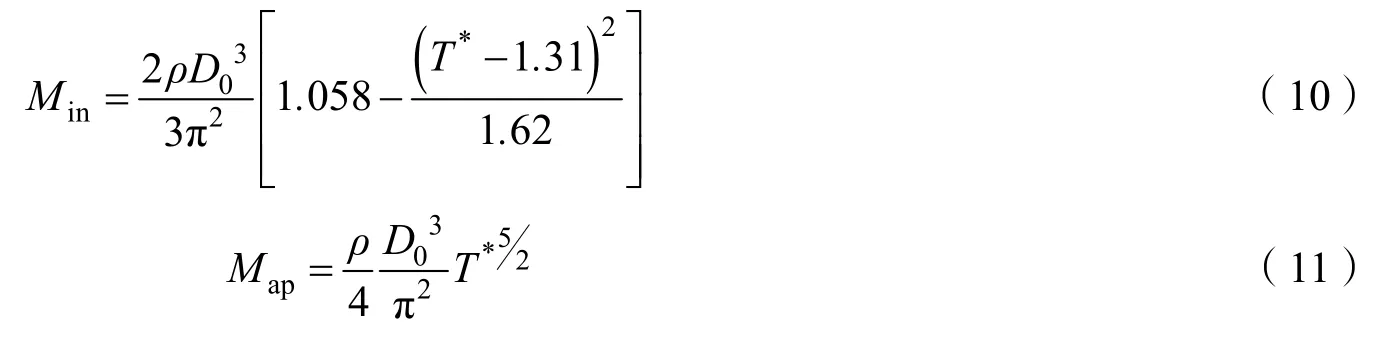
式中 D0指降落傘的名義直徑；T*是歸一化時間，為降落傘的充滿時間。

3.3 充氣半徑計算法

與內含質量計算法類似，充氣半徑計算法亦需要確定降落傘內部所包含的空氣質量，即內含質量。但是與內含質量計算法不同的是，該方法不考慮表觀質量，而是認為附加質量可由降落傘的內含質量乘以相關的參考系數來確定，而關鍵參考系數的取值與充氣半徑的相對變化相關。

如圖2所示，對于軸對稱的降落傘充氣過程可以進行相應的簡化建模，除軸向運動外，對于徑向的運動變化以充氣半徑RC的變化來表征[12-13]。

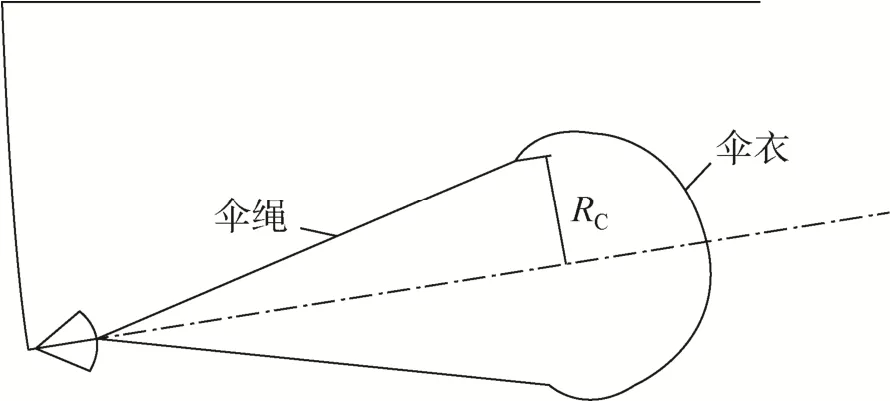
圖2 降落傘充氣過程簡化建模示意Fig.2 Schematic of simplified parachute inflation model

針對圖2所示建模，相應的降落傘附加質量分為徑向附加質量MAr和軸向附加質量MAx，分別由式（12）和式（13）確定。

Macha等人根據多項不同傘型、不同面積降落傘的風洞及飛行試驗數據歸納得出可取為常數，取1.2最為準確；而是充氣初始速度與系統穩降速度之比的平方的函數，并根據試驗數據得到如圖3所示的擬合曲線，可據此曲線選擇并計算得到的大小[14]。需要說明的是，對于有收口控制的降落傘充氣過程，需要分段取值，根據每一階段的不同初始速度選擇對應的。

圖3 軸向附加質量系數初始項擬合曲線Fig.3 Fitted curve of the initial item of the axial added mass coefficient

圖3中，Nh是降落傘充氣初始速度Vi與系統穩降速度Vs之比的平方，即：

降落傘的內含質量由某一時刻降落傘的形狀及尺寸決定，其計算方法可參考上節中對內含質量的計算方法。根據參考文獻[15]，可假設降落傘充氣體積為充氣半徑決定的半球形體積，則也可將降落傘內含質量Min進一步簡化成：

需要說明的是，更準確的做法是參考充氣過程的實際圖像來進行充氣體積的分析計算。如參考文獻[16]，利用空投試驗的錄像，認為某型降落傘在充氣過程中的外形與橢球體接近，用橢球體來估算其充氣體積相比半球與截錐組合體的外形更為準確。

3.4不同工程計算方法的比較分析

對以上三種工程計算方法的特點及各自適用性進行比較，推薦采用充氣半徑法用于降落傘附加質量的計算，見表1所示。

表1 降落傘附加質量工程計算方法的比較Tab.1 Comparison of engineering calculation methods for the parachute added mass

4 降落傘附加質量計算的應用

對于降落傘工程應用而言，附加質量的計算其作用主要體現在兩個方面：

第一，物傘系統動力學仿真分析中必須考慮附加質量。相關研究表明，當物體的密度遠大于周圍流體的密度時，附加質量效應可以近似忽略；當物體密度和周圍流體密度相差不大時，動力學建模就必須考慮附加質量的影響。由于降落傘采用柔性特紡材料制作，其平均密度與空氣密度相當。因此，建立降落傘的動力學仿真分析模型時必須考慮附加質量。

第二，確定降落傘作用力需要考慮附加質量。計算得到降落傘附加質量后，通過上文式（2）可以進一步得到降落傘的作用力。對于降落傘強度設計而言，最為關鍵的還是要確定降落傘的最大開傘載荷，一般發生在傘衣充氣張滿的時刻。當前，對于無限質量情況的降落傘開傘，工程上往往采用動載系數法計算降落傘的最大開傘載荷；對于有限質量情況的降落傘開傘，又往往在動載系數的基礎上再乘以開傘動載縮減系數來確定最大開傘載荷。對于不同的降落傘傘型，其動載系數、動載縮減系數均是基于試驗數據歸納得出的。對于部分非常成熟、具備大量試驗數據的降落傘傘型具備這些動載系數的參考數據，但是對于新的傘型設計而言則缺乏數據支持。因此，根據降落傘運動的客觀規律來計算降落傘作用力才具備普適性，而這就需要確定附加質量的計算方法。

對于物傘系統動力學仿真分析而言，可以在建模中將附加質量矩陣參照本文所述的工程計算方法來確定。按照本文描述的充氣半徑計算法，可以確定附加質量矩陣中的質量項。

但是，對于附加質量矩陣中的慣性矩項，目前還沒有充氣半徑計算法對應的參考系數取值，建議按照降落傘充氣形狀對應的空氣來計算附加慣性矩。例如，假設降落傘充氣體積為充氣半徑決定的半球形體積，則附加慣性矩可按式（17）來計算。

對于降落傘最大開傘載荷計算的應用，以某降落傘減速裝置為例。

該減速裝置采用一頂質量為0.17kg、名義面積為0.35m2、阻力面積為0.122 5m2的錐形帶條傘，以實現對14kg的回收物進行穩定減速。回收物在海拔高度1 800m、飛行速度400m/s、彈道傾角–81°條件下彈射開傘。

按照上文所述充氣半徑計算法可以計算得到該降落傘的附加質量，在充氣張滿時（即無因次充氣半徑取為1）的徑向及軸向附加質量可計算得到分別為0.024 7kg、0.031 4kg，分別為降落傘自身質量的14.5% 和18.5%。進一步基于式（2）進行計算，可以得到充氣張滿時降落傘軸向力（即最大開傘載荷）為10.56kN。而對于錐形帶條傘，此為無限質量情況，可取 1.05的動載系數，則計算得到的最大開傘載荷結果為10.57kN，兩者基本一致。由此可見，利用本文所述充氣半徑計算法計算降落傘的附加質量并從而進一步計算降落傘的開傘載荷是完全可行的，并且具備更為廣泛的應用價值。

5 結束語

基于附加質量的概念和降落傘的特性，在降落傘的動力學分析中必須考慮附加質量的影響。基于勢流理論、邊界元法或者利用CFD專業軟件可以對降落傘的附加質量進行數值計算，但由于降落傘充氣階段具有大柔性體快速大變形的特點，為了確定各時刻的充氣形狀，還需要通過流固耦合方法進行計算，或者通過試驗圖像進行識別和擬合。由于數值計算工作量大且非常復雜，為了滿足工程需要，本文結合對國內外相關文獻的歸納分析，重點給出了確定降落傘附加質量的幾種工程計算方法。根據對不同方法的對比，作者認為充氣半徑計算法具備較好的應用價值。

在得到降落傘附加質量后，可以進一步計算得到降落傘的作用力，從而為降落傘的設計提供依據。從本文提供的案例可以看出，基于附加質量求解最大開傘載荷與已知動載系數計算的最大開傘載荷非常接近。由于動載系數法計算最大開傘載荷受限于已知成熟傘型的經驗數據，對于無動載系數的其它傘型設計而言，通過附加質量的計算并進一步獲取降落傘作用載荷是有效的解決途徑。

對于物傘系統動力學仿真分析而言，按照本文描述的充氣半徑計算法可以確定附加質量矩陣中的質量項。但是，對于慣性矩項，目前還缺乏充氣半徑計算法對應的參考系數取值，當前降落傘各類試驗中也還難以獲取相關的參數，因此還需開展更為深入的研究。事實上，目前國內外文獻中鮮見關于降落傘附加質量慣性矩項如何確定的具體描述，文中給出了按照降落傘充氣形狀充滿的空氣來計算附加慣性矩的初步建議，可供相關科技人員參考。

References)

[1]USBALLDO F, DEARMAN J, MORRIS A. Proposed Framework for Determining Added Mass of Orion Drogue Parachutes[R]. NASA 20110011303, 2011.

[2]王利榮. 降落傘理論與應用[M]. 北京: 宇航出版社, 1977: 26-39. WANG Lirong. Parachute Theory and Application[M]. Beijing: China Astronautics Press, 1977: 26-39. (in Chinese)

[3]熊菁, 秦小波, 程文科. 降落傘附加質量的研究[J]. 中國空間科學技術, 2002, 22(4): 32-38. XIONG Jing, QIN Xiaobo, CHENG Wenke. The Added Mass Research in Parachute System[J]. Chinese Space Science and Technology, 2002, 22(4): 32-38. (in Chinese)

[4]KNACKE T W. Parachute Recovery Systems Design Manual[M]. Santa Barbara: Para Publishing,1992: 5-39.

[5]SAHIN I, JAN W C, KENNARD P W. Added Mass Calculations by a Low-order Panel Method[R]. AIAA 1993-0788, 1993.

[6]劉丹, 王曉亮, 單雪雄. 平流層飛艇的附加質量及其對飛艇運動的影響[J]. 計算機仿真, 2006, 23(6): 52-56. LIU Dan, WQNG Xiaoliang, SHAN Xuexiong. Added Mass to Stratospheric Airship and Its Effect on Motion[J]. Computer Simulation, 2006, 23(6): 52-56. (in Chinese)

[7]傅慧萍, 李杰. 附加質量CFD計算方法研究[J]. 哈爾濱工程大學學報, 2011, 32(2): 148-152. FU Huiping, LI Jie. Numerical Studies of Added Mass Based on the CFD Method[J]. Journal of Harbin Engineering Uni-versity, 2011, 32(2): 148-152. (in Chinese)

[8]周景軍, 李育英, 項慶睿. 一種水下航行體附加質量數值計算方法[J]. 魚雷技術, 2013, 21(4): 246-249. ZHOU Jingjun, LI Yuying, XIANG Qingrui. A Numerical Computation Method of Additional Mass for Underwater Vehicle[J]. Torpedo Technology, 2013, 21(4): 246-249.

[9]ELGABAILI M, KENNETH J D. Added Mass of a Model Round Parachute Canopy during Inflation[R]. AIAA 2013-1321, 2013.

[10]賈華明, 李健. 收口十字形降落傘充氣過程動力學建模與仿真[J]. 航天返回與遙感, 2012, 33(5): 16-23. JIA Huaming, LI Jian. Modeling and Simulation of Inflation Process Dynamics of Reefed Cruciform Parachute[J]. Spacecraft Recovery & Remote Sensing, 2012, 33(5): 16-23.

[11]DAVID J C. Apparent Mass Its History and Its engineering Legacy for Parachute Aerodynamics[R]. AIAA 1991-0827-CP, 1991.

[12]LINGARD J. The Effects of Added Mass on Parachute Inflation Force Coefficients[R]. AIAA 1995-1561, 1995.

[13]WOLF D. A Simplified Dynamic Model of Parachute Inflation[R]. AIAA 1973-450, 1973.

[14]MICHAEL J M. A Simple, Approximate Model of Parachute Inflation[R]. AIAA 1993-1206, 1993.

[15]王海濤. 大型降落傘抽打現象及運動穩定性研究[D]. 長沙: 國防科學技術大學, 2011. WANG Haitao. Research on Bull Whipping and Dynamic Stability of Large Parachute System[D]. Changsha: National University of Defense Technology, 2011. (in Chinese)

[16]BROOK A K. Parachute Drag Area Using Added Mass as Related to Canopy Geometry[R]. AIAA 2009-2942, 2009.

[17]魯媛媛, 榮偉, 吳世通. 火星環境下降落傘拉直過程的動力學建模[J]. 航天返回與遙感, 2014, 35(1): 29-36. LU Yuanyuan, RONG Wei, WU Shitong. Dynamic Modeling of Parachute Deployment in Mars Environment[J]. Spacecraft Recovery & Remote Sensing, 2014, 35(1): 29-36. (in Chinese)

[18]龔文軒. 降落傘附加質量與開傘動載[J]. 航空學報, 1995, 16(1): 84-86. GONG Wenxuan. Parachute Added Mass and Opening Forces[J]. Acta Aeronautica et Astronautica Sinica, 1995, 16(1): 84-86. (in Chinese)

Calculation Methods of Added Mass of Parachute

HUANG Wei1,2

（1 National University of Defense Technology, Changsha 410073, China）
（2 Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）

The canopy force is an important parameter of the parachute opening process. Calculating canopy force is based on drag character performance of the canopy and added mass method, by modeling recovery system dynamic equation, and computing the load change during parachute opening. Thus, the precision of the added mass is crucial for the parachute opening force calculation. In the past, the researching added mass was based on the assumption of ideally inflated canopy shape, using the added mass coefficient method, however, the research of the establish method of the added mass coefficient has never been developed. This paper gives a description of the added mass of parachute, including its concept, spacecraft-parachute system motion equation, numerical calculation, and two engineering calculation methods for canopy added mass i.e. inner mass method and inflation radius method. Through the comparison between the two engineering calculation methods, the inflation radius method can be used to calculate the radial and axial added mass of parachute, so it is better to use the method to determine the added mass for engineer.

parachute; aerodynamic deceleration; added mass; return technique

V244.21+6

: A

: 1009-8518(2016)02-0042-09

10.3969/j.issn.1009-8518.2016.02.006

黃偉，男，1977年生，2002年獲中國空間技術研究院飛行器設計專業碩士學位，現在國防科技大學航天與材料工程學院攻讀博士學位，研究方向為航天器進入、減速與著陸。E-mail：13811005923@139.com。

（編輯：陳艷霞）

2015-04-29

國家重大科技專項工程