基于ARIMA模型的裝備器材需求預測方法

劉旭陽， 吳龍濤， 周萬里

(1. 裝備學院研究生管理大隊， 北京 101416； 2. 裝甲兵工程學院技術保障工程系， 北京 100072； 3. 73668部隊， 江蘇 南京 211131)

基于ARIMA模型的裝備器材需求預測方法

劉旭陽1,2， 吳龍濤2， 周萬里3

(1. 裝備學院研究生管理大隊， 北京 101416； 2. 裝甲兵工程學院技術保障工程系， 北京 100072； 3. 73668部隊， 江蘇 南京 211131)

分析了裝備器材需求的影響因素，建立了裝備器材需求時間序列的求和自回歸移動平均(Auto Regressive Integrated Moving Average, ARIMA)模型，提出了基于ARIMA模型的裝備器材需求預測方法，進行了實例分析，并與傳統的預測方法進行了對比。結果表明:模型的預測精度明顯優于傳統的預測方法，且具有方差預測的優勢。

裝備器材； 需求預測； 求和自回歸移動平均

隨著裝備訓練任務量的增加、訓練強度的增大，以及各種不確定性因素的增多，裝備器材消耗規律更加復雜[1]。當前各級部門在擬制裝備器材申請計劃時，仍依據維修任務和消耗定額，采用定額計算法來確定裝備器材需求量，各級倉庫器材積壓問題比較嚴重，而裝備器材滿足率卻不盡如人意。

近年來，我軍裝備器材管理部門借助信息系統積累了大量的歷史數據。因此，通過建模分析，尋求裝備器材消耗規律并對其需求進行預測已成為可能。傳統的移動平均法和指數平滑法[2]只能對趨勢顯著的序列進行確定性分析；灰色預測模型[3]雖能很好地解決小樣本預測問題，但對于波動性較大的數列，其預測精度仍然不是很高；Croston法[4]和Bootstrap法[5]為間斷性需求預測最常采用的方法，但預測效果不穩定；基于因素分析的預測方法大多采用回歸分析[6]、人工神經網絡[7]和支持向量機[8]等方法，從訓練樣本中提取各因素與需求量的關系，其預測準確性依賴于樣本的容量和質量；基于可靠性的預測方法首先需要根據失效機理假設裝備器材服從不同的壽命分布[9]，然后再依據假設建立裝備器材配置模型，該方法忽略了可靠性之外的其他因素對裝備器材需求的影響，且若假設有誤，則誤差很大。

裝備器材需求時間序列是各種確定性因素和隨機因素綜合作用的結果，對這種時間序列進行統計分析并建立量化模型[10]，可發掘其中蘊含的有效信息。求和自回歸移動平均 (Auto Regressive Integrated Moving Average, ARIMA) 模型是一種重要的時序分析方法，模型擬合和短期預測精度高，在經濟、金融等領域已得到了廣泛應用[11-13]。為此，筆者對裝備器材需求影響因素進行分析，建立裝備器材需求時間序列的ARIMA模型，并應用該模型對某裝甲旅倉庫的維修器材需求進行預測，驗證該模型的有效性。

1 裝備器材需求影響因素分析

裝備器材需求與裝備動用、維修活動密切相關，需求的變化受多方面因素的影響，其中既有確定性因素，如裝備動用、裝備維修等，又有隨機性因素，如環境氣候、人員素質等。

裝備動用時間和強度是影響裝備器材需求的重要因素，由于不同季節的訓練強度和內容不同，使裝備器材需求具有季節性；同時，隨著演習等任務的增加、訓練強度的增大，近年來裝備器材需求量呈現增大的趨勢。裝備器材的可靠性、裝備動用環境、氣候以及使用人員素質等則具有更多的不確定性，進而使裝備器材需求出現隨機波動。

裝備器材需求是上述各因素綜合作用的結果，基于因素分析的預測方法或基于可靠性的預測方法很難對裝備器材需求進行全面準確的預測。因此，筆者從時序分析的角度，利用ARIMA模型的優勢建立裝備器材需求預測模型。

2 ARIMA模型構建

ARIMA模型的實質是差分運算與自回歸移動平均 (Auto Regressive Moving Average, ARMA) 模型的結合，通過適當階數或步數的差分實現非平穩序列的平穩化，然后對差分后序列擬合ARMA模型。圖1為ARIMA模型的構建流程。

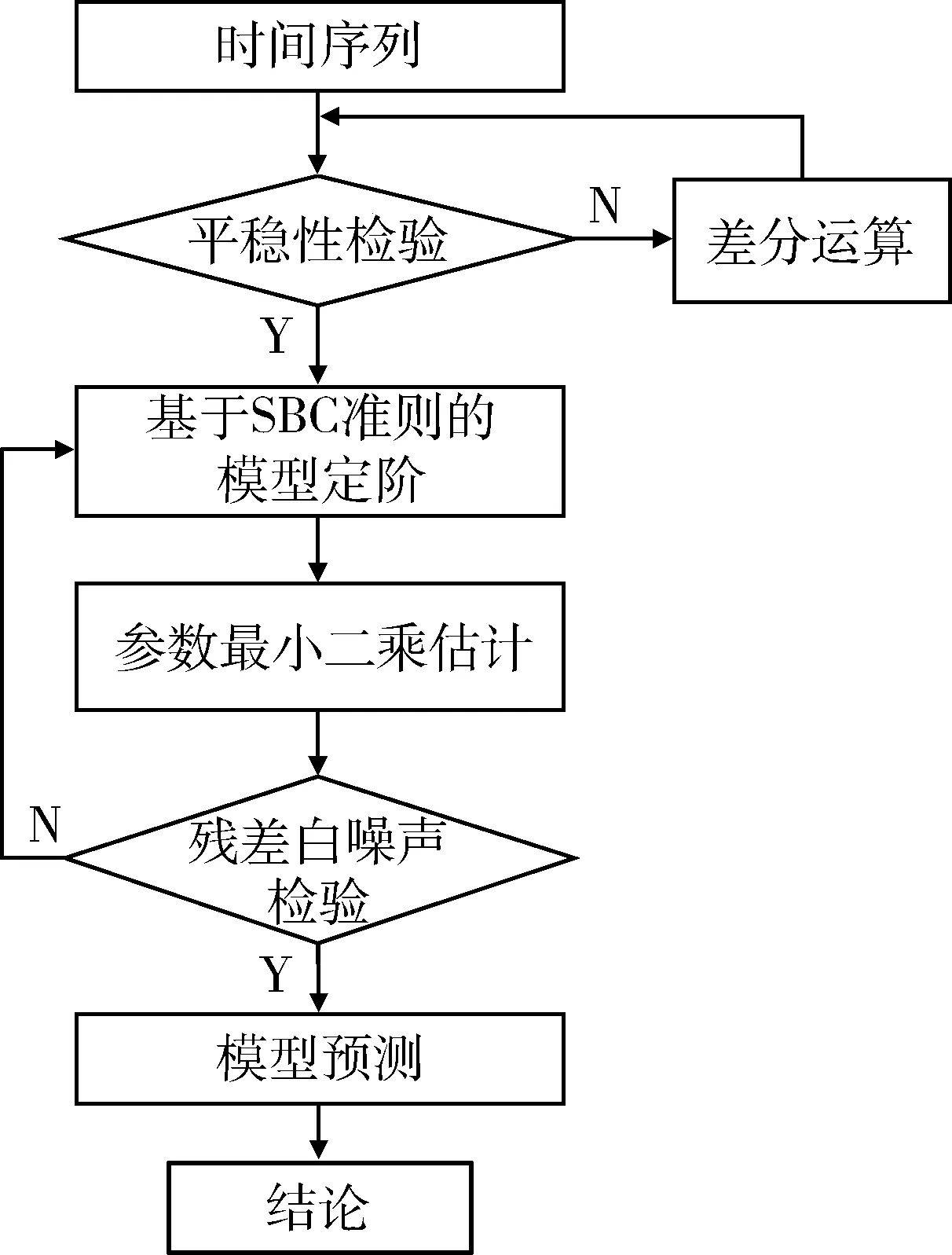
圖1 ARIMA模型構建流程

2.1 時間序列平穩性檢驗及處理

平穩時間序列具有常數均值和方差等統計特性，對于非平穩序列，需經過變換處理后才能構建擬合模型。圖檢驗法根據時序圖、自相關系數和偏自相關系數圖的特征進行平穩性判別，操作簡單，是常用的平穩性檢驗方法[10]。

差分運算可充分地提取非平穩序列中的趨勢性和周期性等信息，是一種有效的平穩化處理方法。對于顯著的線性或曲線趨勢，可進行低階差分運算；而步長為周期長度的差分運算，可較好地提取周期信息。差分階數d可根據觀測序列時序圖的趨勢和季節效應決定，以通過平穩性檢驗為準。

2.2 ARIMA模型定階和參數估計

中心化ARIMA(p,d,q)模型結構為

(1)

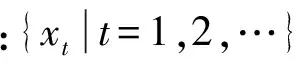
(2)

式中：Φ(B)和Θ(B)分別為自回歸和滑動平均系數多項式。

對于p和q的定階問題，傳統的圖定階法主觀性強且不精確。崔建國等[13]利用遺傳算法進行定階，但該方法過度追求擬合精度，確定的p和q值過大，不利于參數估計，因為擬合精度越高，模型參數就越多；而參數越多，參數估計的難度就越大,精度就越低。SBC(Schwartz Bayes Criterion)準則[10]應用似然函數衡量擬合精度，并從擬合精度和參數個數2個角度來評價擬合模型，即S=-2ln(極大似然函數值)+ln(n)(參數個數)。為此，筆者引入SBC準則，并在一定范圍內遍歷p和q值，當S值最小時，即為實現擬合精度和參數個數之間最佳平衡的相對最優模型。對于中心化ARIMA(p,d,q)模型，其對數似然函數滿足條件

(3)

又因為模型參數個數為p+q+1，所以模型的SBC函數值為

(4)

對于p+q+1個未知參數的估計，常用的矩估計法比較粗糙，精度不高；極大似然估計精度較高，但必須已知裝備器材需求的總體分布函數。由于條件最小二乘估計法不需要已知裝備器材需求的總體分布函數，且估計精度較高，因而筆者采用該方法進行參數估計。

2.3 殘差序列的白噪聲檢驗

理想擬合模型的殘差序列應為白噪聲序列，不含任何相關性信息。因此，需對殘差序列進行白噪聲檢驗。首先計算樣本的自相關系數

(5)

式中：k=1,2,…,n-1，其中n為序列長度。

然后構造LB統計量進行白噪聲檢驗，即

(6)

2.4 基于ARIMA模型的裝備器材需求預測

(7)

式中：

最小預測方差為

(8)

(9)

3 實例分析

某裝甲旅維修器材倉庫負責保障該旅裝甲裝備小修、檢修、維護保養以及伴隨保障等所需的維修器材。裝備動用情況為影響該倉庫器材需求的主要因素，裝備訓練多集中在夏、秋季節，維修任務相對集中，因而器材需求較冬、春季節偏多。以倉庫中S器材2011-2014年逐月的需求數據為例，采用筆者提出的器材需求時序模型進行擬合分析和預測。

3.1 裝備器材需求時間序列的平穩性檢驗及差分處理

圖2為S器材需求觀測序列時序圖。可以看出：S器材的月消耗觀測序列具有明顯的線性遞增趨勢，且以1年為周期進行波動，是典型的非平穩序列。

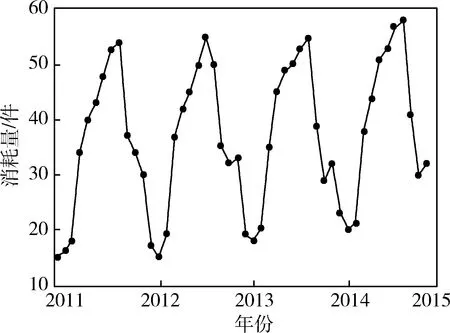
圖2 S器材需求觀測序列時序圖

通過差分運算對序列進行平穩化處理，依次進行1階趨勢差分和12步周期差分運算。圖3為S器材需求差分序列相關分析。可以看出：器材需求時間序列沒有明顯趨勢或周期，自相關系數相關性表明序列具有2階短期相關性，因此差分后序列基本平穩。

3.2 模型定階和參數估計

由圖3可以看出：自相關系數和偏自相關系數均具有2階截尾性，因此在0≤p≤2和0≤q≤2范圍內，依據SBC值最小準則確定模型階數，結果如表1所示。選擇ARMA(0,2)模型對S器材差分后需求序列進行擬合。

應用條件最小二乘估計法對未知參數進行估計，可得擬合模型為

(10)

進一步變換處理可得

圖3 S器材需求差分序列相關分析

表1 基于SBC準則的模型定階

xt=xt-1+xt-12-xt-13+εt-

0.597εt-1-0.381εt-2。

(11)

式中：xt為t時期S器材需求觀測值；白噪聲序列εt～N (0,2.3192) 。

3.3 殘差序列的白噪聲檢驗

為擬合模型的殘差序列構造LB統計量，應用SAE統計分析軟件進行殘差的白噪聲檢驗，結果如表2所示，可以看出：延遲各階的LB統計量的P值均顯著大于α (α=0.05)，表明所構建的ARIMA擬合模型有效。

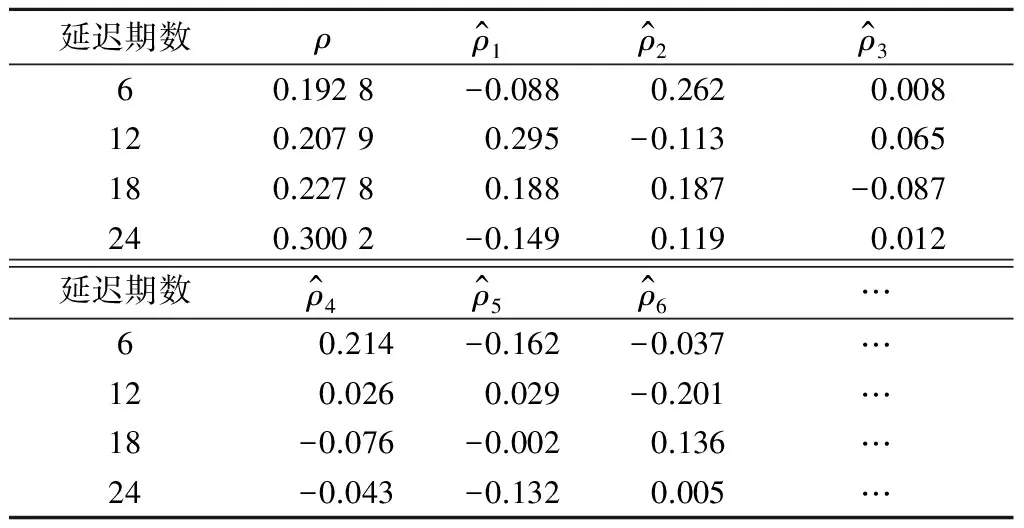
表2 殘差的白噪聲檢驗

3.4 預測結果對比分析

基于S器材2011-2014年的需求數據，分別利用移動平均法、指數平滑法 (平滑系數為0.5)、灰色GM (1,1)模型和筆者提出的ARIMA擬合模型對S器材2015年各月的需求量進行預測，并與實際需求量進行對比，結果如圖4所示。

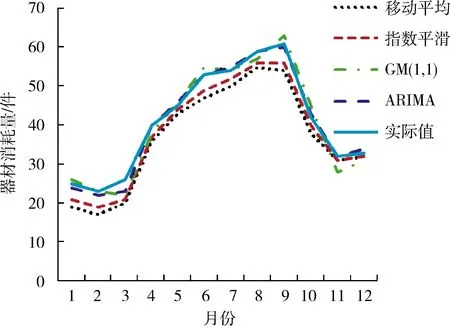
圖4 S器材2015年各月的需求預測結果對比

4種方法預測值的平均絕對百分比誤差(Mean Absolute Percentage Error, MAPE)和年度需求量預測誤差對比結果如表3所示。其中：MAPE的計算公式[14]為

(12)

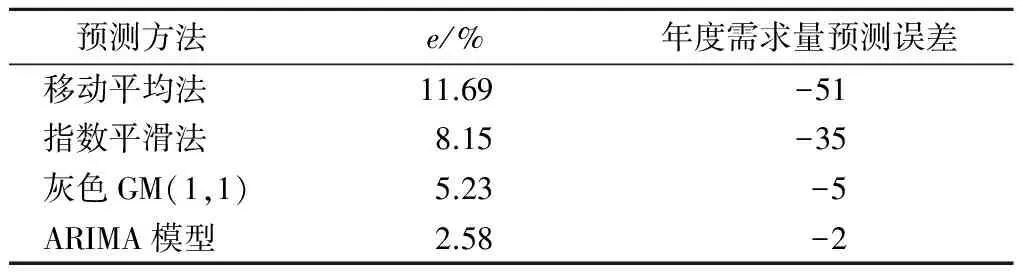
表3 4種方法預測結果的誤差對比

由圖4和表3可以看出：基于ARIMA模型的預測效果最佳，其次為灰色GM (1,1) 模型，而指數平滑法和移動平均法的預測準確性相對較差。這是因為：灰色GM (1,1) 模型、指數平滑法和移動平均法只能對時間序列中的趨勢性進行預測；而ARIMA模型對時間序列中的趨勢性和季節性都能很好地進行預測。

ARIMA模型除了對需求均值進行預測外，還可預測需求方差，從而便于計算器材需求的概率分布函數和后續庫存控制建模。如在各月需求相互獨立的假設下， 根據式 (8)，可得2015年度裝備器材需求的預測方差為74.278。

4 結論

裝備器材需求發生過程受各種確定性因素和隨機因素的影響，傳統的預測方法很難進行全面、準確的預測。當前利用ARIMA模型進行需求預測的研究并不多見，筆者提出了基于ARIMA模型的裝備器材預測方法，可很好地對經常性消耗器材進行需求預測。但在研究過程中也發現：對于某些需求波動特別大的裝備器材，該方法預測效果并不理想。其原因主要是這些器材需求時間序列的殘差序列具有異方差性。下一步，將針對這一特性進行深入研究。

[1] 蔡麗影,毛豐超,王凱,等.美陸軍兩級維修體制改革及啟示[J].裝備學院學報,2014,25(5):40-44.

[2] 齊馳,侯忠生.自適應單指數平滑法在短期交通流預測中的應用[J].控制理論與應用,2012,29(4):465-469.

[3] 郭曉君,劉思峰,吳利豐.污染物減排預測的灰色Markov組合模型與算法[J].計算機應用研究,2013,20(12):3670-3673.

[4] Snyder R D,Ord J K,Beaumont A.Forecasting the Intermittent Demand for Slow-moving Inventories:A Modeling Approach [J].International Journal of Forecasting,2012,28(6):485-496.

[5] Willemain T R,Smart C N,Schwarz H F.A New Approach to Forecasting Intermittent Demand for Service Parts Inventories [J].International Journal of Forecasting,2004,20(1):375-387.

[6] 牛京考.基于主成分回歸分析法預測中國鐵礦石需求[J].北京科技大學學報,2011,33(10):1177-1181.

[7] Venkatesh K,Ravi V,Prinzie A.Cash Demand Forecasting in ATMs by Clustering and Neural Networks [J].European Journal of Operational Research,2014,232(3):383-392.

[8] Carbonneau R,Laframboise K,Vahidov R.Application of Machine Learning Techniques for Supply Chain Demand Forecasting [J].European Journal of Operational Research,2008,184(5):1140-1154.

[9] Kamath K R,Pakkala T P M.A Bayesian Approach to a Dynamic Inventory Model under an Unknown Demand Distribution [J].Computers and Operations Research,2002,29(1):403-422.

[10] 王燕.應用時間序列分析[M].2版.北京:中國人民大學出版社,2012：148-156.

[11] Arunraj N S,Ahrens D.A Hybrid Seasonal Autoregressive Integrated Moving Average and Quantile Regression for Daily Food Sales Forecasting [J].International Journal of Production Economics,2015,170(4):321-335.

[12] Lee Y S,Tong L I.Forecasting Time Series Using a Methodology Based on Autoregressive Integrated Moving Average and Genetic Programming [J].Knowledge-based Systems,2011,24(1):66-72.

[13] 崔建國,趙云龍,董世良,等.基于遺傳算法和ARMA模型的航空發動機壽命預測[J].航空學報,2011,32(8):1506-1511.

[14] Syntetos A A,Boylan J E.The Accuracy of Intermittent Demand Estimates [J].International Journal of Forecasting,2005,21(2):303-314.

(責任編輯: 王生鳳)

Equipment Material Demand Forecasting Method Based on ARIMA Model

LIU Xu-yang1,2, WU Long-tao2, ZHOU Wan-li3

(1. Brigade of Postgraduate Management, Equipment Academy, Beijing 101416, China; 2. Department of Technical Support Engineering, Academy of Armored Force Engineering, Beijing 100072, China; 3. Troop No.73668 of PLA, Nanjing 211131, China))

The factors affecting the equipment material demand are analyzed, and an Auto Regressive Integrated Moving Average (ARIMA) model of equipment material demand time series is built. A forecasting method of equipment material demand based on ARIMA model is presented, the example is analyzed and compared with the traditional prediction methods. The results show that the proposed model performs better than the traditional methods in forecasting accuracy, and has the advantage of variance forecasting.

equipment materials; demand forecasting; ARIMA

2016-10-18

軍隊科研計劃項目

劉旭陽(1978-)，男，講師，博士研究生。

E92

：ADOI：10.3969/j.issn.1672-1497.2016.06.005

1672-1497(2016)06-0021-05