基于阻抗測量的孤島檢測方案

張嘉蕾,田 寰

（1、山西大學，太原，030013；2、山西省電力勘測設計院，太原，030001）

基于阻抗測量的孤島檢測方案

張嘉蕾1,田 寰2

（1、山西大學，太原，030013；2、山西省電力勘測設計院，太原，030001）

本文對單相光伏并網發電系統的孤島檢測方案進行了研究。結合goertzel算法，采用注入諧波電流法進行電網基波阻抗估計，并詳細給出了推導過程和結論。

孤島檢測;阻抗測量法;goertzel算法

0 引言

根據德國標準VDE0126中規定：當電網中斷供電后，光伏并網發電系統要在5s內檢測出電網阻抗提高1Ω，并進行孤島保護。所以要進行孤島保護，就需要測量電網阻抗。現有阻抗測量法分為被動式測量和主動式測量，被動式測量是利用電網本身存在的次諧波來計算電網阻抗。

1 阻抗測量法

1.1 goertzel算法

goertzel算法是離散傅里葉變換的一種快速算法，它可計算指定頻率點的信號功率譜，計算結果與離散傅里葉變換DFT和快速傅里葉變換FFT相差不大，且大大減少了運算量，故本文通過goertzel算法計算公共耦合點電壓和逆變器輸出電流在指定頻率處的諧波含量。

goertzel算法對于指定頻率點相當于一個匹配濾波器，其線性微分方程為：

式中，X[n]為輸入信號當前采樣點時刻的值，S[n]為中間變量當前采樣點時刻的值，S[n-1]為中間變量前一個采樣點時刻的值，S[n-2]為中間變量前兩個采樣點時刻的值，Y[n]為goertzel算法的輸出變量當前采樣點時刻的值，n=（0,1,2...N-1）。經過遞歸運算便可得到輸入信號在該頻率點的幅值信息Y[N]，Y[N]的幅值平方為：

1.2 諧波阻抗估計基波阻抗

當斷路器閉合，逆變器和電網保持連接時，電網可看作一個容量無窮大的電壓源，由于電網阻抗很小，則公共耦合點處的基波電壓、諧波電壓可分別近似為：

公共耦合點處的基波等效阻抗、諧波等效阻抗分別為：

當斷路器斷開，逆變器和周圍負載形成孤島供電系統時，則公共耦合點處的基波電壓、諧波電壓可分別近似為：

公共耦合點處的基波等效阻抗、諧波等效阻抗分別為：

通過計算公共耦合電壓和電流的諧波含量可得到公共耦合點處的諧波等效電抗。通過諧波阻抗Zpcc(h)估計基波阻抗Zpcc。負載品質因數Qf，負載諧振角頻率w分別定義為：

根據標準VDE0126規定Qf不應小于2，負載基波電抗為：

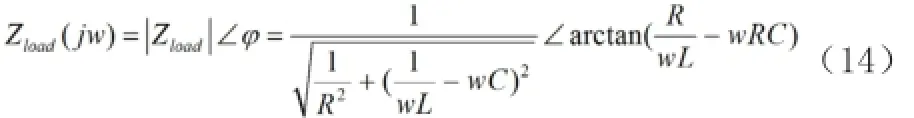
注入h次諧波后，負載諧波阻抗為：

代入Qf后，將式（15）轉換為式（16）。

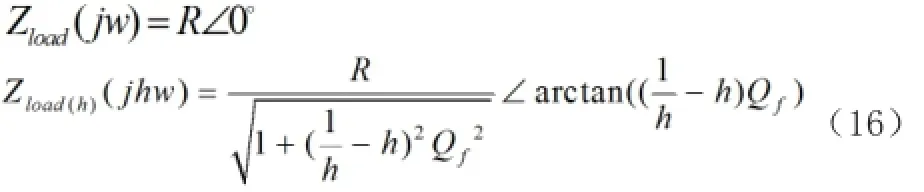
可得：

P為多機光伏系統輸出的總有功功率，U為電網電壓有效值。

通過上述推導可知，由式（12），通過goertzel計算Vpcc和Iinv在指定頻率處的諧波含量，得到負載的諧波阻抗，再由式（17），通過負載的諧波阻抗乘以相應的系數m，便可估計負載的基波阻抗。

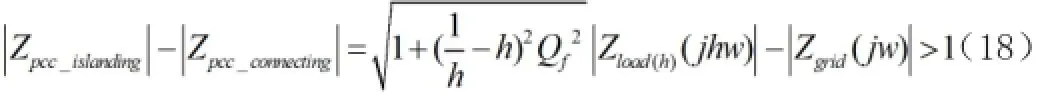
式（18）中，電網阻抗一般很小可忽略，由負載的基波阻抗便可估算電網基波阻抗。根據VDE0126標準，通過監測公共耦合點處的基波阻抗是否產生1Ω的跳變，便可判斷是否產生孤島。

2 仿真驗證

通過PSIM軟件對所提的基波阻抗估計法進行了仿真驗證。本文注入1/2次諧波，系數m=3.88。由于標準中只規定了整數次諧波的含量，對于非特征次諧波沒有具體規定，因此只能依據注入總諧波含量的THD不能超過5%來限制諧波含量的注入。

2.1 單機系統仿真驗證

單機仿真電路參數如下：單機有功功率為775W，參考電流幅值為5A，濾波電感為40mH，濾波電容為0.1μF，諧波含量取0.02，電網阻抗（0.5+0.002j）Ω，逆變器開關頻率和采樣頻率同為20kHz，本地負載品質因數為2.5，本地負載R、L、C分別為62Ω、79mh、128μF。

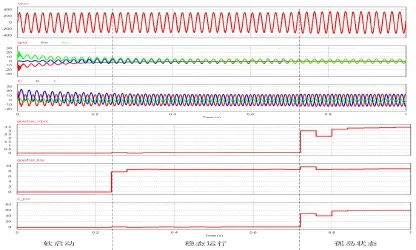
圖1 單機系統仿真波形

整個仿真過程分為三個階段分別是軟啟動，穩態運行和孤島狀態，如圖1所示。圖中，Ipcc：本地負載總電流，Igrid：電網的電流，Iinv：逆變器輸出電流，Ir：電阻電流，Ic：電容電流，IL：電感電流，goertzel_Vpcc：采用goertzel算法計算得到的Vpcc的1/2次諧波的含量，goertzel_Iinv：采用goertzel算法計算得到的Iinv的1/2次諧波的含量，Z_pcc表示PCC點的基波阻抗。

單機系統中，當軟啟動結束后開始監測Zpcc的變化。在穩態運行時Vpcc的諧波含量很小，幾乎為零，Iinv的諧波含量保持不變，故Z_pcc很小。在0.7s時斷開斷路器QF，模擬孤島效應，在0.72s時測得Zpcc=61.4Ω，產生大于1Ω的跳變，判斷已發生孤島效應。Zpcc在孤島狀態時是本地負載，本地負載阻抗的實際幅值是62Ω。仿真測得61.4Ω與實際的62Ω相差不大，證明該法可以用以估計電網基波阻抗來判斷孤島狀態。

2.2 雙機系統仿真驗證

雙機PV1和PV2的仿真電路參數：總有功功率為1550W，單機均為775W，諧波含量取0.01，濾波電感為40mH，濾波電容為0.1uF，本地負載R、L、C分別為31Ω、40mh、257μF。

圖2中，Iinv1：PV1中的逆變器輸出電流，Iinv2：PV2中的逆變器輸出電流。Goert_Iinv1：采用goertzel算法計算得到的Iinv1的1/2次諧波的含量，Goert_Iinv2：采用goertzel算法計算得到的Iinv2的1/2次諧波的含量。

雙機系統中，在0.7s時斷開斷路器QF，在0.72s時測得Zpcc=32.1Ω，產生大于1Ω的跳變，判斷已發生孤島效應。本地負載阻抗的實際幅值是31Ω。仿真測得32.1Ω與實際的31Ω相差不大，證明該法適合多機系統。

圖2 雙機系統仿真波形

3 結論

通過仿真驗證本文所提的估計電網基波阻抗的方法確實可靠準確，且適用于多機系統。該法的局限性在于主要針對RLC并聯諧振負載，對于其他類型負載不適用。但由于其他類型負載可以容易檢測到1Ω的跳變，所以在實際使用時可以考慮與其他方法結合。

任碧瑩，一種特定次諧波阻抗的孤島檢測方法研究[J]，電力電子技術，2015.02.029

An island detection scheme based on impedance measurement

Zhang Jialei1,Tian Huan2
（1,Shanxi University, Taiyuan,030013；2.Shanxi Electric Power Survey and Design Institute,Taiyuan, 030001）

In this paper,the single phase photovoltaic grid connected generation system is studied. Based on the Goertzel algorithm,this method is used to estimate the fundamental impedance of the electric network, and the process and conclusion are given in detail.

impedance measurement method;Goertzel algorithm