反厄米特矩陣的一些特征

曹元元，張　騫，毛　亮

(湖北師范學院 數學與統計學院,湖北 黃石　435002)

反厄米特矩陣的一些特征

曹元元，張騫，毛亮

(湖北師范學院 數學與統計學院,湖北 黃石435002)

摘要：研究了反厄米特矩陣(A*=-A )的相關性質,并給出了反厄米特矩陣的一些充要條件.

關鍵詞：厄米特矩陣；反厄米特矩陣；廣義逆

中圖分類號：O153

文獻標識碼：A

文章編號：1009-2714(2015)04- 0088- 06

doi:10.3969/j.issn.1009-2714.2015.04.017

收稿日期：2015—09—08

基金項目：國家自然科學基金資助項目(11271105)，湖北省教育廳重點資助項目(D20122202)

作者簡介：曹元元(1989—)，女，陜西渭南人，碩士，研究方向為矩陣分析.

1引言與預備引理

厄米特矩陣和反厄米特矩陣是兩類特殊形式的矩陣,在矩陣理論及其應用中有著非常重要的地位[1～2]. 近幾年,隨著應用的需要和研究的深入,酉矩陣、厄米特矩陣、Hamilton矩陣和廣義逆矩陣之間的關系及其在解矩陣方程中的應用已經取得了豐富的成果[3～4],推廣了酉矩陣、厄米特矩陣及廣義次對稱矩陣的相應結果.特別地,將正交陣的廣義Cayley分解推廣到了k-廣義酉矩陣和k-廣義厄米特矩陣上,從而統一了各類厄米特矩陣及廣義逆矩陣. 本文將進一步研究廣義厄米特矩陣中的一種特殊矩陣——反厄米特矩陣的相關性質和一些充要條件,從而對特殊矩陣的深入研究及其應用提供有益的幫助.

下面先給出一些必要的記號，再給出本文所需要的一些引理.

1)AA+A=A,2)A+AA+=A+,3)AA+=(AA+)*, 4)A+A=(A+A)*.

1)AA#A=A,2)A#AA#=A#,3)AA#=A#A

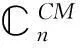
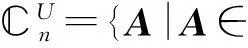
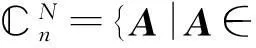
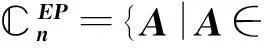
近些年來,國內外許多學者如:Baksalary,Trenkkler,Liu等人運用[8] 中推論6提出的∑-K-L分解解決了許多特殊矩陣的問題,該分解如下:

引理1[8]( ∑-K-L分解) 設A∈n×n,且r(A)=r,則存在酉矩陣U∈n×n使得

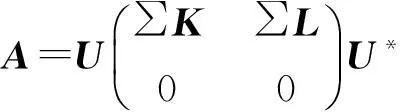
(1)

其中 ∑=diag(σ1Ιr1……,σ1Ir1),σ1>σ2>…>σt>0,r1+r2+…+rt=r,K∈r×r,L∈r×(n-r)且KK*+LL*=Ir.

用 ∑-K-L分解,我們容易得出:

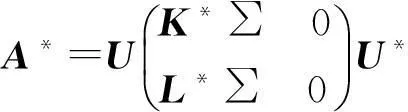
(2)

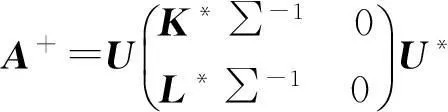
(3)

由∑-K-L分解易知, A#存在 K 為可逆矩陣,且

(4)

運用∑-K-L分解,我們可以給出前面介紹的幾種特殊矩陣的刻畫.

引理2[9]設A∈n×n,且r(A)=r, A有(1)式的分解形式，則：

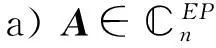
2反厄米特矩陣的有關性質

1985年Roger A. Horn 和 Charles R. Johnson 在[1]中給出了厄米特矩陣和反厄米特矩陣的定義,并研究了厄米特矩陣的性質及特征.類似的我們先給出反厄米特矩陣的一些性質,再給出反厄米特矩陣的有關特征.

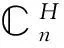
b)σ(A)?i,

αΑα∈i.

b)設α 為矩陣Α的屬于特征值λ的特征向量,即有Αα=λα(α≠0),所以αΑα=αλα=λαα ,又由a)有αΑα∈i,且αα∈+,所以λ∈i,從而σ(A)?i.

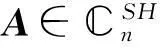
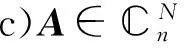
證明a)? b)定理1 a)已給出證明.下面只需證明b) ?c)，c)? d)，d)? a)即可.

(α+β)*A(α+β)=α*Aα+α*Aβ+β*Aα+β*Aβ∈i,α*Aα∈i,β*Aβ∈i

所以αΑβ+β*Aα ∈i.

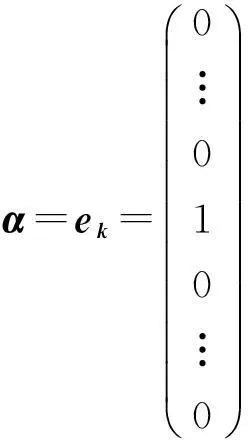
計算可得

α*Aβ+β*Aα=akl+alk∈i

(5)

再令α=ek, β=iel則β*=(0…0,-i,0…0) (第l列為 -i，其余元素全為0的1行n列矩陣),計算可得

α*Aβ+β*Aα=iakl-ialk∈i

(6)

"? " 設AT∈SHn,即(AT)*=(A*)T=-AT=(-A)T,所以A*=-A 即A∈SHn.

下面我們給出反厄米特矩陣的一個性質.

證明設x,y分別為屬于A 的特征值λ1,λ2(λ1≠λ2)的特征向量,若 A∈SHn,則由定理1 b)知λ1,λ2∈i,所以x*(Ay)=x*λ2y=λ2x*y,(Ax)*y=(λ1x)*y=-λ1x*y,且由A*=-A 可得x*(Ay)=x*(-A*)y=-(x*A*)y=-(Ax)*y,所以λ2x*y=-(-λ1x*y)=λ1x*y,即λ2x*y-λ1x*y=(λ2-λ1)x*y=0(λ1≠λ2) 所以x*y=0,即x,y彼此正交.

3反厄米特矩陣的一些特征

下面運用矩陣的∑-K-L分解給出反厄米特矩陣的一些刻畫.

L=0, ∑K=K∑

(7)

從而

K-1∑=K*∑=-∑K

(8)

這樣,由(7)(8)式可得K2=-Ir.

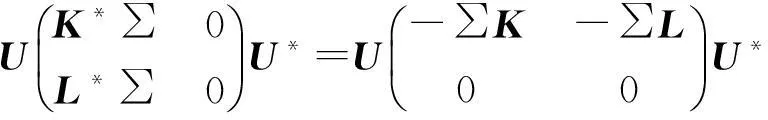
b)AA*=A*A=-A2

c) A2A+=-A*.

證明a) ?b) 由定義直接得出.

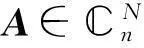
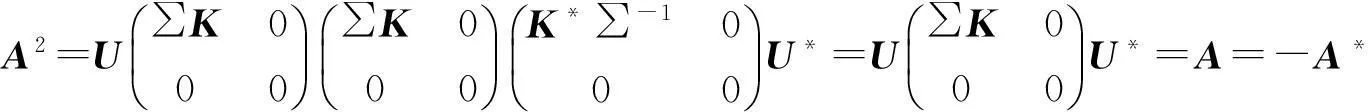
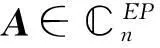
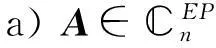
b)A*A+A=-A ,

c)A*AA+=-A ,

d)AA+A*=-A ,

e)AA*A+=-A ,

f) A+A*A=-A ,

g) A+AA*=-A ,

h)A*A+=-AA+,

i)A*A+=-A+A .

證明下面只給出a) ?b), a) ?d), a) ?h)的證明過程，對于a) ?c)可用類似于a) ?b)的方法證明, a) ?e), a)? f), a) ?g), a) ?i)可用類似于a) ?d)的方法證明.

b) ?a)設 A有分解式(1)式,若A*A+A=-A ,則(A) ?(A*),而r(A*)=r(A)所以(A)=(A*), 即矩陣 A∈EPn,由引理2 a)知L=0,所以由A*A+A=-A 結合 (1)(2)(3)計算可得 K*∑=-∑K,從而 A*=-A,即 A∈SHn.

a) ?d)類似于a) ?b)直接計算可得,下證d) ?a):

設A 有分解式(1)式,若AA+A*=-A ,則結合(1)(2)(3)計算有

L=0且K*∑=-∑K ,從而A*=-A ,即A∈SHn.

a) ?h) 類似于a) ?b)直接計算可得,下證h)? a):

設 A有分解式(1)式,若A*A+=-AA+,則結合(1)(2)(3)計算有

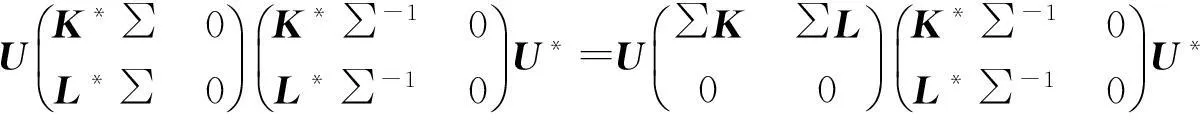
故K*∑K*∑-1=-Ir且 L*∑K*∑-1=0,所以r(K*∑K*∑-1)=r,得r(∑K*∑-1)≥r從而

r(∑K*∑-1)=r,所以L=0 且K*∑=- ∑K,所以A*=-A ,即A∈SHn.

b)A*A#A=-A ,

c)A*AA#=-A ,

d)AA#A*=-A ,

e)A#AA*=-A ,

f)A*A#=-AA#,

g)A*A#=-A#A .

證明下面只給出a)?b),a) ?d),a)? f)的證明，而對于a) ?c)可類似于a) ?b)得到證明, a) ?e) a)? g)可類似于a)? d)得到證明.

a)? d), a) ?e), a)? g)可用類似于a)? f)的方法得到證明.

由引理2 b)知A∈Nn?L=0,∑K=K∑結合(1)(2)(4)計算可得

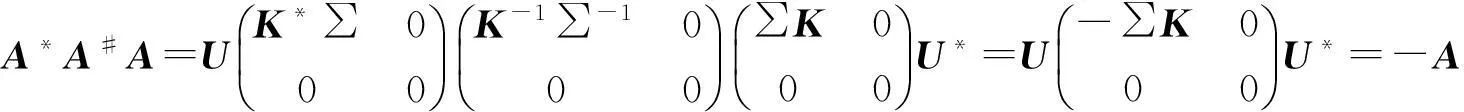
b) ?a)設A 有分解式(1)式,若A*A#A=-A,則R(A)? R(A*)而 ”(A*)=”(A)所以 R(A*)=R(A)，即矩陣 A∈EPn，由引理2(a)可知 L=0,若A*A#A=-A ,則結合(1)(2)(4)計算可得

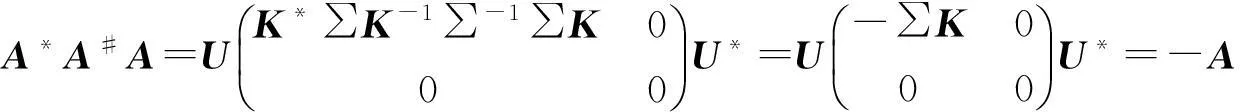
所以L=0 且K*∑=-∑K ,從而A*=-A ,即A∈EPn.

a)? d)類似于a)? b)直接計算可得,下證d)? a):

設A 有分解式(1)式,若AA#A*=-A ,則結合(1)(2)(4)有

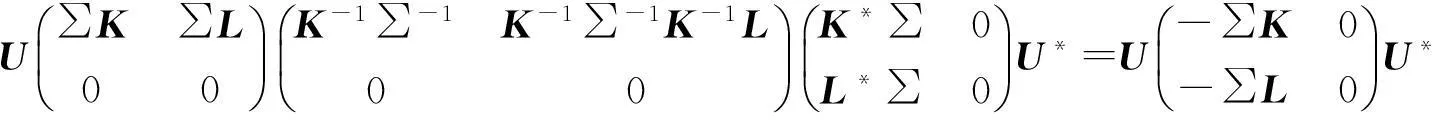
計算可得L=0 且K*∑=-∑K,從而A*=-A ,即A∈EPn.

a) ?f)類似于a) ?b)直接計算可得,下證f) ?a):

設 A有分解式(1)式,若 A*A#=-AA#,則結合(1)(2)(4)有

計算可得 K*∑K-1∑-1=-Ir,且L*∑K-1∑-1=0,所以r(K*∑K-1∑-1)=r,得r(∑K-1∑-1)≥r，從而r(∑K-1∑-1)=r,所以L=0 且K*∑=-∑K,從而A*=-A ,即A∈SHn.

參考文獻：

[1]Horn R A,Johnson C R．Matrix Analysis[M]．London：cambridge University Press，1985.

[2]Jain s K,Gunawardena A D．Linear Algebra[M]．Beijing：china Machine Press，2003.

[3]袁暉坪.廣義酉矩陣與廣義Hermite矩陣[J].數學雜志,2003,23(3):3375~380.

[4]袁暉坪,王行榮.k-廣義Hermite矩陣及其在矩陣方程中的應用[J].吉林大學學報(理學版),2012,50(1): 59~62.

[5]Wang G, Wei Y, Qiao S. Generalized Inverses:Theory and Computation[M].Beijing：Science Press,2004.

[6]Drazin M P. Natural structures on semigroups with involution[J]. Bull Amer Math Soc, 1978,84:139~141.

[7]Mitra S K. Noncore square matrices miscellany[J].Linear Algebra Appl,1996,249:249~260.

[8]Hartwig R E,Spindelb?ck K. Matrices for which A*and A+commute[J].Linear Multilinear Algebra,1984,14:241~256.

[9]Baksalary O M, Styan G P H, Trenkler G. On a matrix decomposition of Hartwing and Spindelb?ck[J]. Linear Algebra Appl, 2009,430(10):2798~2812.

Some proterties of skew-Hermitian

CAO Yuan-yuan，ZHANG Qian，MAO Liang

(College of Mathematics and Statistics,Hubei Normal University,Huangshi435002,China)

Abstract:We study several characteristics of the skew-Hermitian matrix ( A*=-A)in this paper, and gives some sufficient and necessary conditions for the skew-Hermitian matrix.

Key words:Hermitian matrix; skew-Hermitian matrix; generalized inverse