GPS/BDS組合姿態測量及精度分析

王　珍，丁樂樂，黃恩興，馬　強

(天津市勘察院，天津 300191)

Combined GPS/BDS Attitude Determination and Accuracy Analysis

WANG Zhen,DING Lele,HUANG Enxing,MA Qiang

?

GPS/BDS組合姿態測量及精度分析

王珍，丁樂樂，黃恩興，馬強

(天津市勘察院，天津 300191)

CombinedGPS/BDSAttitudeDeterminationandAccuracyAnalysis

WANGZhen,DINGLele,HUANGEnxing,MAQiang

摘要：給出了GPS/BDS組合雙差觀測模型和姿態測量解算算法，采用Kalman濾波進行動態基線解算的參數估計，利用LAMBDA方法固定雙系統模糊度，獲得動態基線固定解，最后通過基線的坐標系轉換獲得姿態角。比較了單系統和GPS/BDS雙系統靜態姿態角與動態短基線解算結果。試驗結果表明，GPS/BDS組合姿態測量的精度和可靠性較GPS單系統都有顯著提高。

關鍵詞：GPS/BDS組合；姿態測量；約束基線；精度

一、引言

隨著美國GPS現代化的實施、俄羅斯GLONASS系統的完善，以及歐洲Galileo和中國北斗二代導航測姿系統的建成, 多系統組合導航測姿越來越受到關注。國內外已有很多學者和機構對多衛星導航系統組合定位測姿進行了研究，并取得了不少成果[1-3]。目前，對GPS/GLONASS組合的研究較多，對GPS/BDS組合定位測姿方面的研究較少。

與單系統測姿相比，多系統組合定位測姿具有以下優勢：①組合系統觀測到的衛星數目顯著增多，衛星空間分布幾何構型更好，能選擇幾何結構更好的衛星組進行測姿，可提高測姿精度和可靠性；②能提高遮擋環境下的可視衛星數，增加了衛星導航測姿的可用性；③觀測更多的衛星能增強測姿的可靠性，觀測到的衛星數越多，系統的抗粗差能力越好，測姿的可靠性也就越高；④多系統組合定位測姿，也將減小對單系統的依賴。

截至2012年12月，我國已成功發射4顆北斗導航試驗衛星和13顆北斗導航衛星，形成了5(GEO)+5(IGSO)+4(MEO)星座，可實現中國及周邊地區的精確導航定位測姿[4-5]。北斗系統正處于組網建設階段，北斗衛星顆數相對較少，測姿的可靠性和精度還不如GPS系統，但是GPS系統在衛星數不足的情況下(如高樓密集的城區)也不能提供連續無縫的導航測姿，GPS/BDS組合定位測姿就有可能解決這一問題[1]。

GPS/BDS組合數據處理過程包括：組合觀測模型的建立、北斗與GPS的時空基準轉換、基線解算及姿態角測量等。比較單系統和GPS/BDS雙系統靜態姿態角和動態短基線解算結果，分析姿態測量的精度和可靠性。

二、GPS/BDS雙差觀測模型構建

GPS/BDS組合雙差觀測模型可以同時結合載波和偽距進行解算。GPS/BDS組合相對定位的觀測方程為[6]

(1)

GPS和北斗系統載波頻率存在差異，因此，筆者采用雙差策略，在各自衛星系統中選取參考星形成雙差觀測值，以保證所有的雙差模糊度為整數。

三、北斗與GPS時空基準轉換

組合定位測姿需要實現兩個系統時空基準的統一，包括時間系統轉換和坐標系統的統一。

北斗時間系統BDT是國際原子時TAI從2006-01-01T00：00：00開始起算的原子時，與國際原子時保持有33s的常數差。GPS時與國際原子時保持有19s的常數差，并在GPS標準歷元1980-01-06T00:00:00時與UTC保持一致。因此，GPS時換算為北斗時間時需要減去14s。

北斗衛星星歷擬合參數是以2000中國大地坐標系為參考建立的，因此，北斗系統測姿的坐標及相對定位中解算的基線向量屬于CGCS2000大地坐標系。GPS測姿的坐標及相對定位中解算的基線向量屬于WGS-84大地坐標系。由于上述兩個坐標系定義上一致，即坐標系原點、尺度、定向及定向演變的定義都是相同的，因參考框架不同而引起的相對定位結果的差異很小，可忽略不計[7]。

四、姿態測量角的獲取

為使獲得的載體姿態角由衛星系統坐標系轉換到載體坐標系。首先需將地固系坐標的空間直角坐標系轉換為空間大地坐標系，即將(X,Y,Z)轉換為大地緯度B和大地經度L。

當地水平坐標系與地固坐標系的轉換關系為

(2)

載體坐標系與當地水平坐標系的轉換關系為

XB=RY(φ)RX(θ)RZ(ψ)XL

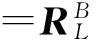
(3)

從轉換矩陣即可獲得姿態角值

(4)

五、數據處理及結果分析

由于試驗條件的限制，本文主要對靜態模擬姿態測量和實際動態姿態測量進行解算。

試驗1為2012年4月17日UTC0:00:00—UTC23:59:30用和芯星通公司生產的雙頻雙系統接收機采集的靜態觀測數據，采樣率為30 s。靜態試驗兩測站分別命名為JT01、JT02。

試驗2為動態試驗，是2011年12月30日進行的車載試驗，車頂前后固定兩個接收機天線，數據采集時間段為UTC4:27:44—UTC7:30:00。動態試驗兩測站分別命名為DT01、DT02。

1. 衛星星座及可見性分析

首先對比分析了衛星分布、可見衛星數以及GDOP的情況。圖1中給出了GPS和北斗試驗1 UTC12:00:00的衛星天空視圖。

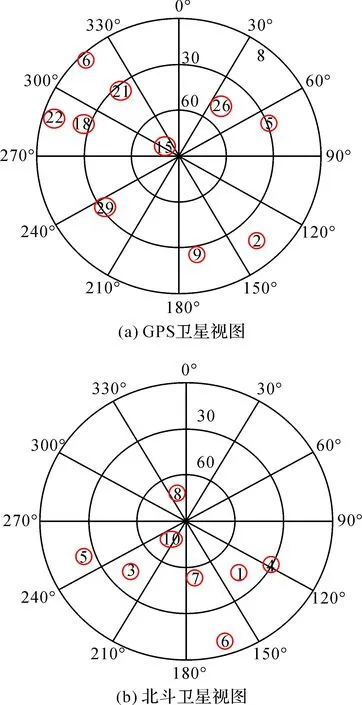
圖1　GPS與北斗衛星天空視圖

從圖1中可以看到，當時的GPS可視衛星數為10顆，其中高度角大于10°的衛星占8顆；北斗可視衛星數為8顆，高度角大于10°的衛星為7顆，且集中分布在一側，這與當前我國北斗衛星導航系統目前工作的星座有關，因為序號為1、3、4、5的北斗衛星為地球同步衛星(GEO)，而序號為6、7、8、10的北斗衛星為地球傾斜圓軌道衛星(IGSO)。試驗數據采集時，北斗中軌衛星(MEO)只有一顆試驗衛星，且觀測時間段內沒有觀測值。

2. 靜態模擬姿態測量及結果分析

圖2為試驗1中JT01—JT02姿態角分別采用單系統和GPS/BDS雙系統組合動態解算的結果航向角和俯仰角上的時序圖。

圖2　車載試驗天線

圖3給出了單基線解算條件下，單GPS系統姿態解算和GPS/BDS組合姿態解算對比結果。基線長度約為11.027 m，從圖中可以看出，航向角的解算精度要高于俯仰角解算精度。由統計精度可知，單GPS系統航向角精度為0.010°，GPS/BDS組合精度為0.006 7°；單GPS系統俯仰角精度為0.037 7°，GPS/BDS組合精度為0.026 8°。GPS/BDS組合的姿態解算精度要高于單GPS解算姿態精度。

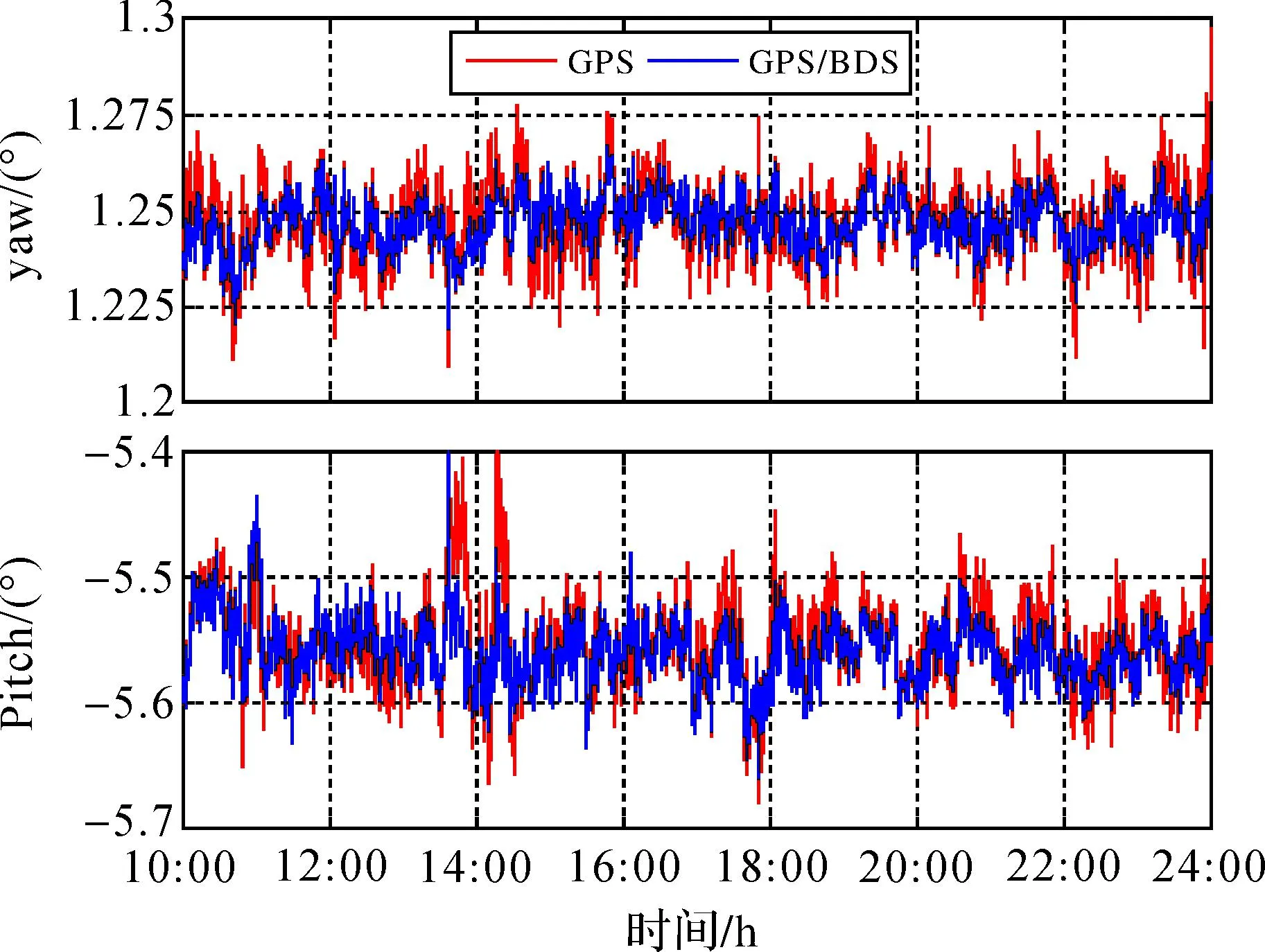
圖3　GPS和GPS/BDS姿態解算結果對比

3. GPS/BDS組合動態相對測姿結果及統計分析

下面給出試驗2中車載動態測姿的試驗結果，由于當時北斗系統不夠穩定，單北斗動態數據解算結果中存在少數較大的粗差，為了方便與GPS的測姿結果和組合結果進行比較，結果中剔除了單北斗不能固定模糊的部分歷元的測姿結果。動態基線解算的真值無法確定，在車載試驗中，車上兩天線間的距離保持不變。圖4為車載試驗的航跡圖。由于一根副天線沒有接收北斗數據，因此試驗數據處理只能采用單基線處理模式。此時，單基線只能通過直接求解法給出航向角和俯仰角。車載試驗未加載慣導設備，動態姿態元素未知，車載移動過程中其基線長度為固定值，因此試驗結果通過基線長度的動態解進行驗證。

圖4　車載試驗軌跡

圖5中的基線解算給出了將近3 h的動態基線測量結果。從圖中可見，基線長度有3處出現了跳變，這可能是由于接收機天線沒有固定緊有微小移動所致。由測姿結果可知，GPS/BDS組合短基線解算較單系統基線解算精度有所提高。從分布圖可以看出，基線解算長度集中在2.03～2.05 m之間，GPS/BDS組合解算的基線長度統計最為集中。

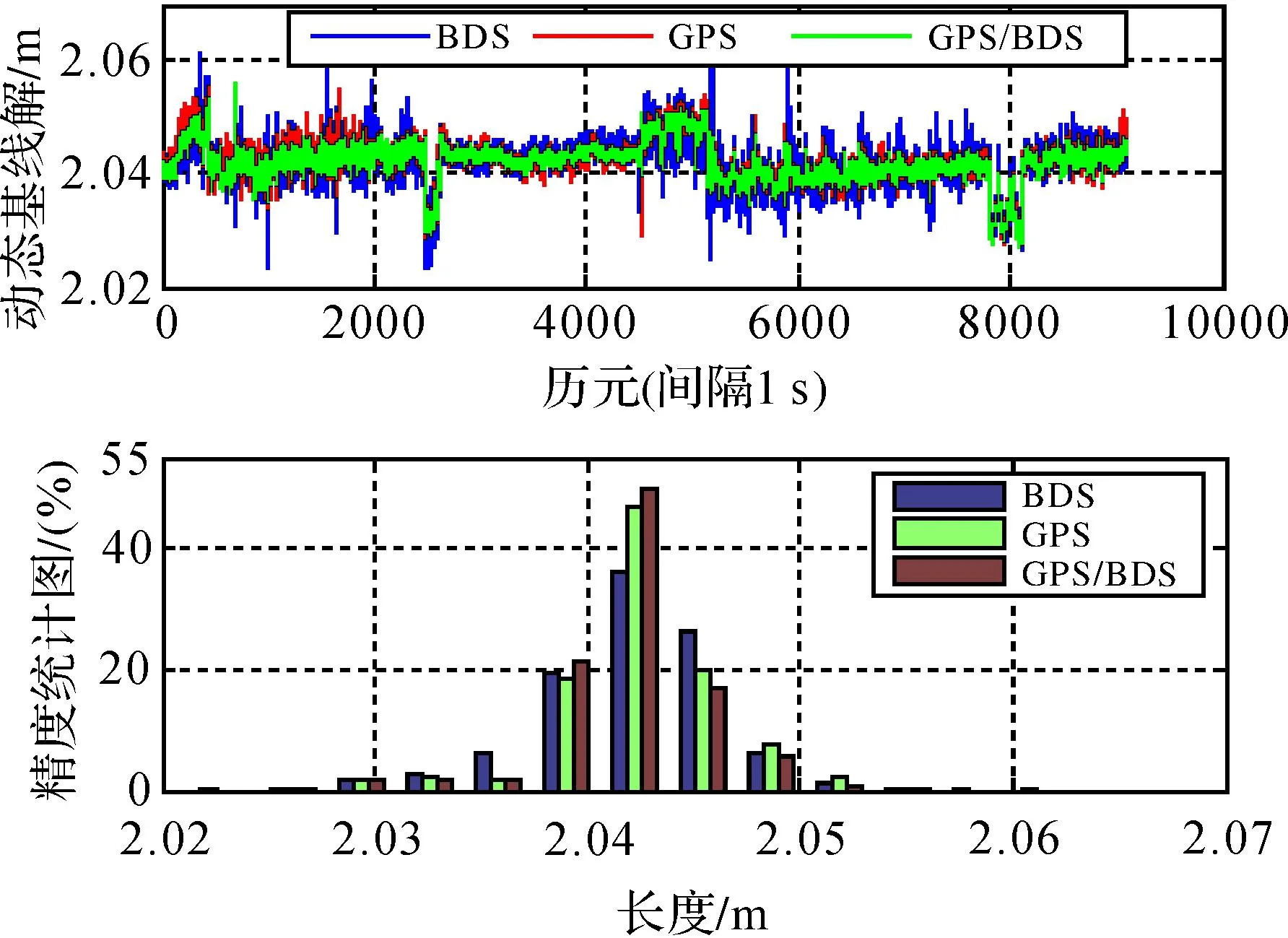
圖5　動態基線解算及精度統計

六、結論

GPS/BDS組合姿態測量精度和可靠性較GPS單系統有所提高。從誤差源考慮，北斗與GPS觀測值精度相當，但北斗的GEO衛星在武漢地區的衛星高度角基本上都在30°以上，避免了低衛星高度角造成的電離層和對流層延遲誤差的影響；從數學計算上看，觀測值誤差可看作隨機誤差，GPS/BDS組合較單系統增加了觀測方程的個數，從而提高了基線解算的精度和可靠性。

參考文獻：

[1]高星偉, 李毓麟, 葛茂榮. GPS/GLONASS相位差分的數據處理方法[J]. 測繪科學, 2004, 29(2): 22-24.

[2]蔡昌盛, 戴吾蛟, 匡翠林, 等. 單頻GPS/GLONASS組合單點定位的精度評估[J]. 大地測量與地球動力學, 2011, 31(3): 85-89.

[3]張小紅, 郭斐, 李星星, 等. GPS/GLONASS組合精密單點定位研究[J]. 武漢大學學報: 信息科學版, 2010, 35(1): 9-12.

[4]譚述森. 衛星導航定位工程[M]. 北京: 國防工業出版社, 2010.

[5]萬祥, 張孟陽. 北斗高動態雙頻相對定位技術[J]. 飛行器測控學報, 2010, 29(3): 68-73.

[6]李征航, 黃勁松. GPS測量與數據處理[M]. 武漢: 武漢大學出版社, 2005.

[7]魏子卿. 2000中國大地坐標系及其與WGS84的比較[J]. 大地測量與地球動力學, 2008, 28(5): 1-5.

[8]KIM D, LANGLEY R B. Kalman-filter-based GPS Ambiguity Resolution for Real-time Long-baseline Kinematic Applications[C]∥Submitted to the Workshop of the Central European Initiative (CEI) Working Group on “Satellite Navigation Systems”, The Chair of Satellite Geodesy and Navigation. Olsztyn, Poland: Warmia and Masuria University, 2000.

[9]YANG Y, HE H, XU G. Adaptively Robust Filtering for Kinematic Geodetic Positioning[J]. Journal of Geodesy, 2001, 73(2-3): 109-116.

[10]TEUNISSEN P J G. Least-square Estimation of the Integer GPS Ambiguities[C]∥IAG General Meeting.Beijing: [s.n.], 1993.

[11]WANG J L. Stochastic Modeling for Real-time Kinematic GPS/GLONASS Positioning[J]. Navigation, 1999, 46(4): 297-305.

[12]WANG J L, RIZOS C, STEWART M P, et al. GPS and GLONASS Integration: Modeling and Ambiguity Resolution Issues[J]. GPS Solutions, 2001, 5(1): 55-64.

[13]DAI L W, HAN S W, WANG J L, et al. A Study on GPS/GLONASS Multiple Reference Station Techniques for Precise Real-time Carrier Phase-based Positioning[C]∥Proceedings of the 14th International Technical Meeting of the Satellite Division of the Institute of Navigation, Salt Lake City, UT: Salt Palace Convention Center, 2001: 392-403.

引文格式： 王珍，丁樂樂，黃恩興，等.GPS/BDS組合姿態測量及精度分析[J].測繪通報，2015(6)：53-56.DOI:10.13474/j.cnki.11-2246.2015.0177

作者簡介：王珍(1975—)，男，高級工程師，主要從事GPS測量與數據處理工作。E-mail：wangzhen1026@126.com

收稿日期：2014-05-19

中圖分類號：P228.4

文獻標識碼：B

文章編號：0494-0911(2015)06-0053-04