基于同一性的健壯CS分類算法

陳　赟，林　峰

(1. 重慶郵電大學 移通學院，重慶 合川 401520；

2.重慶郵電大學 電子信息與網絡工程研究院，重慶 400065)

摘　要：針對利用壓縮感知(CS)進行信號分類識別的問題，提出了一種聯合欲分類信號和樣本信號的健壯CS分類算法。該方法通過引入“同一性”的概念，克服了信號過完備字典傳統構造方式的不足，增強了信號稀疏表示與信號類別間的關聯性，提升了基于壓縮感知的信號分類算法性能。仿真實驗證明了所提方法的正確性，并進一步表明：在非最優過完備字典下，該方法較之傳統CS分類算法更具有分類準確度。

關鍵詞：壓縮感知；信號分類；稀疏表示；同一性

doi:10.3969/j.issn.1002-0802.2015.06.012

基于同一性的健壯CS分類算法

陳赟1，林峰2

(1. 重慶郵電大學 移通學院，重慶 合川 401520；

2.重慶郵電大學 電子信息與網絡工程研究院，重慶 400065)

摘要：針對利用壓縮感知(CS)進行信號分類識別的問題，提出了一種聯合欲分類信號和樣本信號的健壯CS分類算法。該方法通過引入“同一性”的概念，克服了信號過完備字典傳統構造方式的不足，增強了信號稀疏表示與信號類別間的關聯性，提升了基于壓縮感知的信號分類算法性能。仿真實驗證明了所提方法的正確性，并進一步表明：在非最優過完備字典下，該方法較之傳統CS分類算法更具有分類準確度。

關鍵詞：壓縮感知；信號分類；稀疏表示；同一性

doi:10.3969/j.issn.1002-0802.2015.06.012

收稿日期：2015-01-08；修回日期：2015-04-19Received date:2015-01-18；Revised date：2015-04-19

中圖分類號：TN911.7

文獻標志碼：碼：A

文章編號：號：1002-0802(2015)06-0687-05

Abstract：Aiming at the problem of CS(Compressive Sensing) for signal recognition, a robust CS classification algorithm in combination with test sample and training samples is proposed. By introducing the concept of identity into signal processing，some deficiencies of traditional construction mode for signal over-complete dictionary are overcome,and the correlation of between signal sparse representations and signal classes is also enhanced, thus the performance of classification algorithm based on compressive sensing is improved. Simulation results verify the correctness of the proposed algorithm, and further show that this algorithm enjoys higher classification accuracy than traditional CS classification methods under non-optimal over-complete dictionary condition.

作者簡介：

A Robust CS Classification Algorithm based on Identity

CHEN Yun1，LIN Feng2

(1. College of Mobile Telecommunication，Chongqing University of Post and Telecommunications，

Hechuan Chongqing 401520，China; 2. Electronic Information and Networking Research Institute,

Chonging University of Posts and Telecommunications，Chongqing 400065，China)

Key words：compressive sensing; signal classification; sparse representation; identity

0引言

信號分類是模式識別技術非常重要的一項應用，廣泛存在于現代通信的各個領域。例如：信號調制區分、敵我身份研判、運行狀態監測、語音文字鑒別等。最近，由Candès、Donoho以及Tao等數學家提出的壓縮感知理論(CS，Compressive Sensing)[1]逐漸被應用于信號的模式識別。該理論的核心觀點是：通過求解一個非線性最優化問題，稀疏信號可由少量的觀測值(采樣值)準確重構[1-2]。Wright J等人基于該理論首先提出將人臉圖像分辨問題轉化為測試樣本在訓練樣本集中的最稀疏表示問題[3]，即求解最小L1范數問題。由此，逐漸發展出基于信號稀疏表示的一類新型智能模式識別方法。

研究表明，信號稀疏表示分類算法(本文稱為CS分類算法)對噪聲以及樣本維度均具有較好的魯棒性。較之模板匹配[4]、支持向量機[5]等，該方法在模式識別領域具有較好的應用前景。然而，CS分類算法的性能極大程度地依賴于信號的過完備字典。只有合適的過完備字典才能保證信號足夠的稀疏度，從而保證非線性逼近時信號分類的準確度。

本文主要研究CS分類算法中過完備字典構造以及分類準則問題，對信號的特征提取與選擇不作詳細討論。傳統CS分類算法預先構造的過完備字典并不直接包含欲分類的信號，這種方式存在固定[6-11]、適應性差[6-7]或學習復雜[12-14]等缺點。針對以上問題，本文提出將欲分類信號修改為新原子插入到各類信號所對應的過完備字典原子庫中，即Identity Perspective- Compressed Sensing (IP-CS)分類算法。該方法基于同一性觀念，將欲分類信號看成是各類信號的同體(同一類型)，彼此越是相似，外部差異性就越小；通過比較插入(信號)原子對信號稀疏表示的影響進行分類識別。仿真實驗重點對比了上述兩種方法在非最優過完備字典下的分類性能，證明了所提IP-CS分類算法的有效性與可行性。

1傳統CS分類思想

考慮共有k類的欲識別信號，將所有類型的訓練樣本組成過完備字典如下：

ψ=[ψ1,ψ2,…,ψk]=

[v11,…,v1n1,d1,v21,…,v2n2,…,vk1,…vknk]∈Rm×n

(1)

其中ψi是第i類訓練樣本集，vij是第i類中第j個訓練樣本；j=1,2,…,ni；m是樣本的維度。

基于假設：任一測試樣本可由其同類(訓練樣本)線性表出，因此測試樣本x可用過完備字典表示為：

x=ψs0∈Rm

(2)

其中s0是最理想條件下稀疏表示的系數向量。

CS分類的一般步驟[5-16]為：首先，通過變換矩陣對信號進行線性測量；其次，求解最小L1范數問題尋找最稀疏表示；最后，計算最優非線性逼近分類信號。上述分類操作的兩個關鍵是：過完備字典構造和分類準則。通常的做法是：尋找最匹配的樣本構造字典和計算稀疏表示最小殘差決策分類。

如何找到信號最佳的樣本是非常困難的，傳統CS分類算法基于人工或學習方式的字典構造(更新)方式要取得較好的分類效果，要么以字典的“可適性”要么以字典的“復雜性”為代價，并且仍然過度依賴于樣本的“匹配度”。當外界條件發生改變時，過完備字典一旦變得不再“合適”，最小殘差分類準則也就不再可靠。

2IP-CS分類算法

基于同一性壓縮感知(IP-CS)分類算法，繼承了傳統稀疏表示分類思想，但在過完備字典構造以及分類準則兩方面有所改變。這種改變實際是一種簡單有效的字典學習方式，它將欲分類信號本身也參與分類決策，而不是僅僅依靠同類型的原子模板。同時，分類決策基于整個隨機矩陣集合也更加準確、可靠。IP-CS分類算法具體步驟如下。

2.1過完備字典構造

根據傳統CS分類算法，首先(基于人工或學習)將所有k類訓練樣本組成如(1)式所示字典，以此作為IP-CS分類算法的初始默認過完備字典。

然后，計算字典中各類型原子的樣本均值為：

(3)

其中ni是第i類原子vi的樣本數目。

考慮任何一個新測試樣本x∈Rm×1，計算該信號對應的所有k個類型的同體(同一類型)原子為：

(4)

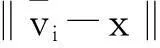
不失一般性，將產生的新原子(同體原子)分別插入對應的訓練樣本集末尾：

(5)

更新初始默認過完備字典如下：

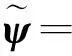
[v11,…,v1n1,d1,v21,…,v2n2,d2,…,

vk1,…vknk,dk]∈Rm×n′

(6)

其中n′=n1+…+nk+k。由于同體原子di跟隨測試樣本每次變更，因此式(6)所示過完備字典具備動態更新特點。

同理，測試樣本x重新用過完備字典可表示如下：

(7)

而s′0=[0,…,0,si1,si2,…sini,sdi,0,…,0]T∈Rn仍是最理想條件下稀疏表示的系數向量。

2.2稀疏解

根據壓縮感知理論，選擇高斯隨機矩陣(滿足RIP性質[1])作為變換矩陣Ф∈Rd×m，并且將變換矩陣的每一行都作歸一化處理。

考慮噪聲與誤差，測試樣本x的觀測值為：

(8)

使用截斷牛頓內點法(TNIPM)等算法求解以下L1范數問題：

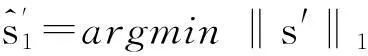
(9)

2.3差異分析

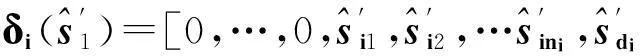
計算線性測量y與δi近似之間的殘差ri′(y)如下：

(10)

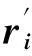
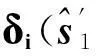
同理，計算線性測量y與δi近似之間的殘差ri(y)如下：

(11)

ri(y)為傳統方法下對各類型間偏差的度量，未考慮新原子貢獻。

(12)

dki用于度量同類型內的偏差，其數值大小反映初始默認過完備字典中各類型訓練信號與其同體原子di之間的相似程度。

計算新原子信號表示向量sh與同體表示向量shi的差異度如下：

(13)

ski用于度量各類型間的偏差，其數值大小反映同體原子所屬種群與測試信號類型的相似程度。

2.4分類

傳統CS算法分類決策僅僅依據最小殘差ri(y)，本文IP-CS算法改進分類準則如下：

首先，基于最小錯誤概率分類原則，算法采用隨機矩陣集合{Фj,j=1,2,…,}來進行健壯地差異分析；式(10)～式(13)采用隨機矩陣Фj計算的結果分別表示為。

其次，定義特征函數δi近似線性測量y的總偏差如下：

(14)

計算所有第i類總偏差平均如下：

(15)

最后，分類決策如下：

(16)

式(16)表示分類線性測量y是基于測試樣本稀疏表示在整個隨機矩陣集合上的最小平均總偏差。

3仿真實驗

特征提取與選擇對模式識別的算法性能有著極大的影響。為公平地檢驗各算法的分類性能，所有算法仿真均采用原始信號本身作為特征。本文實驗信號使用4種(QPSK、2-FSK、4-FSK、16-QAM)不同數字調制方式，采用IP-CS、傳統CS兩種算法進行分類識別。在MATLAB環境下，所有數字調制信號均采用相同的碼元速率(40 kb/s)、采樣頻率(800 kHz)與載波頻率(100 kHz)。計算機仿真進行3組對比實驗，每組實驗(在不同信噪比條件下)各種數字調制方式均產生250個信號樣本，其中50個樣本用于訓練，其余200個樣本則用于測試。其他的主要仿真實驗參數如下：設置錯誤容限ε=0.01，變換矩陣采用高斯隨機矩陣(矩陣行數d=100，共5個)。

3.1無噪聲條件下分類

第一組實驗在無噪聲條件下產生所有實驗信號。傳統CS分類器的過完備字典由200個(每種調制方式50個)信號樣本構成；IP-CS分類器的初始默認過完備字典由196個(每種調制方式49個)信號樣本構成。800個信號樣本用于測試分類算法的性能，仿真實驗結果如表1所示。

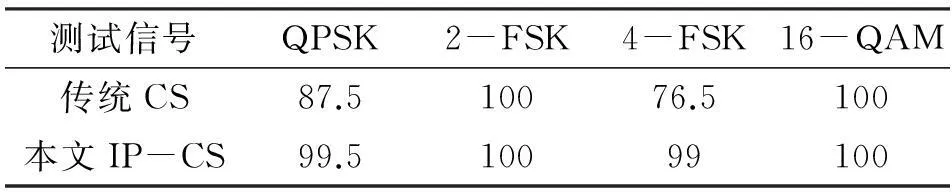
表1　(無噪聲)分類器識別率　(%)

從表1可看出：在理想(無噪聲)條件下，IP-CS算法具有良好的分類準確度。一方面，該算法秉承了傳統CS算法的“稀疏表示”思想，故可同樣用于區分不同類型的信號；另一方面，該算法又引入欲分類信號本身，避免了決策僅僅依靠同類型原子模板的情況。分類決策充分利用同體原子的貢獻(分解系數)，聯合考慮“類間”偏差以及“類內”偏差，因此IP-CS算法的分類錯誤可明顯少于傳統CS算法。

3.2有噪聲條件下分類

考慮一般實際情況，第二組實驗在高斯白噪聲條件下產生所有實驗信號。信噪比從-5 dB到15 dB，每次間隔5 dB，共5種噪聲變化情況。過完備字典構成同上，算法測試仿真實驗結果如圖1所示。

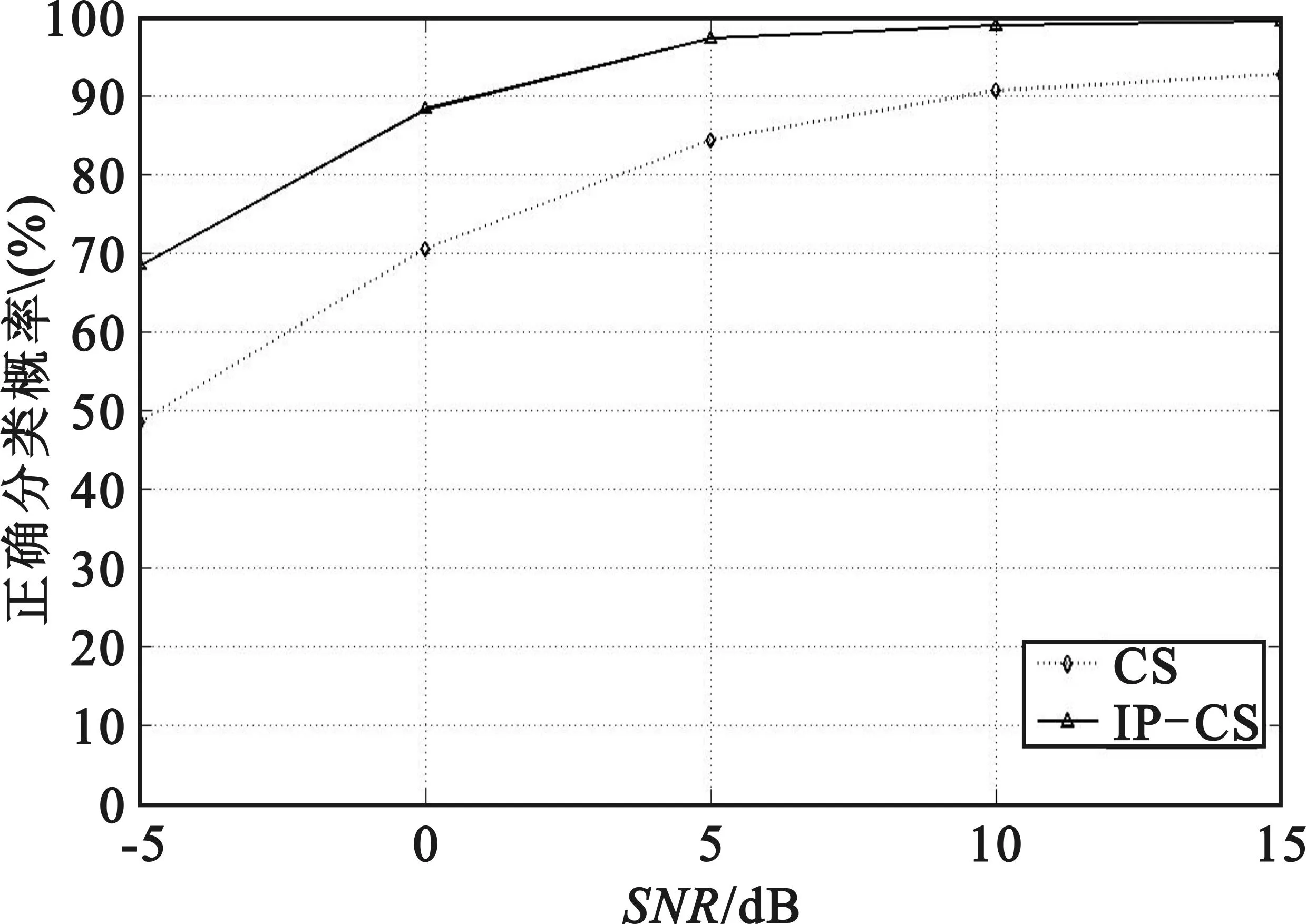
圖1　正確分類的總體概率

圖1給出了兩種算法信號分類的總體性能，即將每次在相同信噪比條件下所有4種不同數字調制信號被正確分類的概率進行算術平均。總體性能是作為衡量分類準確度的重要指標。圖中實線與虛線分別是IP-CS、傳統CS兩種分類算法進行仿真實驗的總體性能曲線。如圖1所示：對比發現兩種算法在同等噪聲環境下，IP-CS分類算法仍具有更好的識別性能。

3.3樣本不匹配條件下分類

進一步考慮復雜情況，第三組實驗在(無噪聲、高斯白噪聲)兩種條件下產生所有實驗信號。當外部環境發生變化時，重點測試分類算法在樣本不匹配情況下的分類性能，以檢驗算法的適應能力。同理，過完備字典構成同上，算法測試仿真實驗結果如表2、表3、表4、表5所示。

表2　(情況1)分類器識別率　(%)

注：情況1——訓練樣本(無噪聲)，測試樣本(信噪比：5 dB)

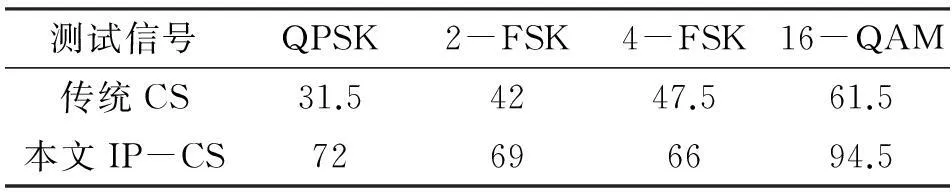
注：情況2——訓練樣本(信噪比：5 dB)，測試樣本(無噪聲)

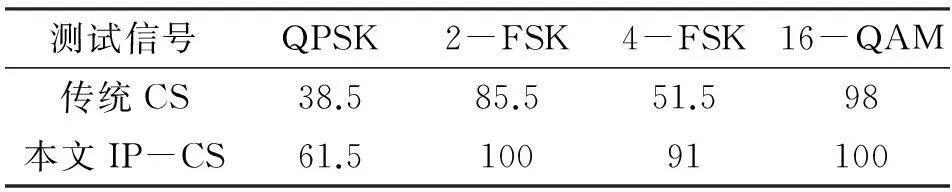
注：情況3——訓練樣本(信噪比：5 dB)，測試樣本(信噪比：-5 dB)

注：情況4——訓練樣本(信噪比：-5 dB)，測試樣本(信噪比：5 dB)

CS分類算法的性能優劣極大程度地取決于(信號特征)過完備字典的“合適性”。在實際中，預先獲得的訓練樣本集不一定能很好反映實際接收信號(受外界影響)的特征。表2、表3、表4、表5比較了當訓練與測試樣本不匹配時兩種分類算法(傳統CS、IP-CS)的適應能力。從表2、表3、表4、表5可看出：IP-CS分類算法具備健壯的識別性能，較之傳統CS分類算法適應性更強。該優勢得益于過完備字典的“動態原子庫”，并且(相同條件下)插入信號同體原子的字典構造(更新)方式簡單有效。因此，針對(條件受限下)非最優過完備字典的使用，信號分類采用IP-CS算法可在一定程度上改善傳統算法可能出現的低識別率狀況。

4結語

壓縮感知(CS)分類是一種新穎的模式識別方法，分類識別基于樣本在過完備字典上的最稀疏表示。本文在此基礎上將稀疏性與同一性有力地結合，提出了將欲分類信號參與分類決策的IP-CS分類算法。通過插入同體原子，該算法構造的動態過完備字典明顯優于傳統靜態固定字典，具有學習簡單、適應性好的優點。同時，IP-CS分類算法改進了過去只重視信號“類間”偏差的最小殘差分類準則，分類決策增加考慮了隨機矩陣集合測量以及“類內”偏差分析。針對數字調制信號的分類仿真，實驗證明了本文所提方法的有效性與可行性。通過對比分析實驗結果，可以發現：在非最優過完備字典情況下，IP-CS分類算法相比傳統CS分類算法展現出了良好的魯棒性。因此，本文所提方法可用于在樣本數量受限、匹配性差、維度過高等實際條件下的信號分類問題。下一步主要工作將深入研究該算法的性能提升以及模式識別推廣問題。

參考文獻：

[1]Candès E. Compressive Sampling[C]//Proceedings of the International Congress of Mathematicians. Madrid: Amer Mathematical Society, 2006: 1433-1452.

[2]Richard G, Baraniuk. Compressive Sensing[J]. IEEE Signal Processing Magazine, 2007, 24(4):118-124.

[3]Wright J, YANG A Y, Ganesh A, et al. Robust Face Recognition via Sparse Representation[J]. IEEE Trans. On Pattern Analysis and Machine Intelligence,2009,31(2): 210-227.

[4]于嫻,賀松,彭亞雄等. 基于GMM模型的聲紋識別模式匹配研究[J].通信技術, 2015，48(01)：97-101.

YU Xian, HE Song, PENG Ya-xiong, et al. Pattern Matching of Voiceprint Recognition based on GMM[J]. Communications Technology, 2015, 48(01): 97-101.

[5]張石清,趙小明,樓宋江等.一種局部敏感的核稀疏表示分類算法[J].光電子.激光, 2014，25(09)：1812-1817.

ZHANG Shi-qing,ZHAO Xiao-ming,LOU Song-jiang,et al. A Classification Algorithm based on Locality-Sensitive Kernel Sparse Representation for Face Recognition[J]. Journal of Optoelectronics.Laser,2014,25(09)：1812-1817.

[6]CHEN Y, LIU J, Lv S T. Modulation Classification based on Bispectrum and Sparse Representation in Cognitive Radio[C]//IEEE 13th International Conference on Communication Technology. Piscataway:IEEE Press,2011:25-28.

[7]SHEN Y, LIU G H, LIU H. Classification of Power Quality Disturbances based on Random Matrix Transform and Sparse Representation[C]//8th World Congress on Intelligent Control and Automation. Piscataway: IEEE Press, 2010: 7-9.

[8]ZHENG C H, ZHANG L, HUANG D S, et al.Metasample-based Sparse Representation for Tumor Classification[J]. IEEE-ACM Trans. On Comput Biol Bioinform, 2011, 8(5): 1273-1282.

[9]呂小聽,李昕,屈燕琴等.基于稀疏表征的話者識別[J].計算機工程與應用，2014，50(20)：215-217，243 .

LV Xiao-ting, LI Xin, QU Yan-qin, et al. Speaker Identification based on Sparse Representation[J]. Computer Engineering and Applications,2014,50(20)：215-217,243.

[10]陸慧娟,陸江江,王明怡等.基于壓縮感知的癌癥基因表達數據分類[J].中國計量學院學報，2012, 23(01)：70-74.

LU Hui-juan, LU Jiang-jiang, WANG Ming-yi, et al. Classification of Cancer Gene Expression Data based on Compressed Sensing[J]. Journal of China University of Metrology, 2012, 23(01)：70-74.

[11]孫道達,趙健,王瑞等.基于稀疏表示的QR碼識別[J].計算機應用，2013，33(01)：179-181，185.

SUN Dao-da, ZHAO Jian, WANG Rui,et al. QR Code Recognition based on Sparse Representation[J]. Journal of Computer Applications,2013,33(01):179-181,185.

[12]廖明熙,張小薊,張歆.基于稀疏表示的水聲信號分類識別[J].探測與控制學報，2014, 36(04)：67-70，77.

LIAO Ming-xi, ZHANG Xiao-ji, ZHANG Xin. Classification and Recognition of Underwater Acoustic Signal Based on Sparse Representation[J]. Journal of Detection & Control, 2014, 36(04)：67-70, 77.

[13]陳思寶,趙令,羅斌.局部保持的稀疏表示字典學習[J].華南理工大學學報自然科學版，2014，42(01)：142-146.

CHEN Si-bao, ZHAO Ling, LUO Bin. Dictionary Learning via Locality Preserving for Sparse Representation[J]. Journal of South China University of Technology(Natural Science Edition), 2014, 42(01)：142-146.

[14]Ptucha R, Savakis A E. LGE-KSVD: Robust Sparse Representation Classification[J].IEEE Trans. On Image Processing,2014,23(04):1737-1750.

[15]王鏗,張重陽,齊朗曄.基于核距離的稀疏表示的交通標識識別[J].計算機應用與軟件，2014，31(03)：146-150.

WANG Keng, ZHANG Chong-yang, QI Lang-ye. Traffic Sign Recognition in Sparse Representation based on Kernel Distance[J]. Computer Applications and Software, 2014, 31(03)：146-150.

[16]Li Y, Yu Z, Bi N, et al. Sparse Representation for Brain Signal Processing : A Tutorial on Methods and Applications[J]. IEEE Signal Processing Magazine, 2014, 31(03):96-106.

陳赟(1981-)，男，碩士，助理講師，主要研究方向為信息處理。

林峰(1978-)，男，碩士，高級工程師，主要研究方向為物聯網、車聯網。