基于二維極值分布的亳州地區強降水概率特征模擬

李佳耘++顧人穎++黃利萍++陳峙君

摘 要：在全球氣候變化的影響下，極端天氣氣候事件頻繁發生。該文結合近年來極端天氣氣候變化研究中應用極值統計理論的新成果，采用亳州4個站建站以來汛期的實測降雨資料，探討了二維Gumbel分布模型，在研究其經驗頻率和理論頻率計算方法的基礎上，根據隨機變量的邊緣分布和條件概率分布，分析了汛期最大強降水雨量及最大過程雨量的聯合分布，建立了其聯合重現期和條件重現期的分布模型，擬合效果很理想。

關鍵詞：極值分布；二維Gumbel分布模型；強降水雨量；過程雨量

中圖分類號 P426.6 文獻標識碼 A 文章編號 1007-7731（2016）01-84-05

Probability Characteristics of Heavy Precipitation Based on Bivariate Gumbel-Logistic Model at

Bozhou Area

Li Jiayun1 et al.

（1BoZhou Meteorological Bureau，Bozhou 236800，China）

Abstract：Frequent climate extremes often occur under changing climate. Using the long-term observed precipitation data，the two-dimension Gumbel model is applied at Bozhou station based on the new theory of extremes statistics. The empirical frequency and theoretical frequency of precipitation extremes are analyzed，and then the joint distribution of the heaviest precipitation and its corresponding heaviest total precipitation is investigated. The models of joint return period distribution and Conditions return period distribution are built，which is useful for the studies of precipitation extremes.

Key words：Extreme distribution；Bivariate Gumbel model；Heavy precipitation；Course precipitation

強降水實際上涉及到降水的歷時、強度、面積、深度等多方面的時空分布特征，它既有一定的持續時間，又占據一定的區域面積或范圍，更有量級和強度大小，因而這類極值問題僅僅運用一維極值分布模式來描述其特征，并不能滿足實際工作的需要，而應用二維或多維極值分布模式描述其全方位特征則更為恰當。近年來，國際上已有不少學者利用二維極值分布模式研究區域和單站強降水概率特征，以便描述表征2個及2個以上變量同時達到極值的隨機現象的概率問題。早在20世紀60年代，Gumbel等人[4-5]在一維Gumbel分布的基礎上即已提出了Gumbel分布的二維形式，但并未引人注目。其后，由于水利水電工程技術科學的發展，許多學者紛紛研究了各種多變量的聯合分布用于極端降水事件或暴雨事件的概率描述，并提出過各種形式的聯合概率分布模型[6-8]。在國內水文氣象學界除了水文學中有個別應用二維分布模式以外，絕大多數學者在研究水文氣象學極值事件中，也只局限于應用一維極值分布模式，在大氣科學領域運用極值分布模式也都以一維模式為主，僅在某些著述中提到或介紹過國外研究成果[1-3]。本文主要運用二維Gumbel分布研究了強降水過程的概率特征。運用二維概率分布模式的優點在于，它不但能較全面地描述一些極端天氣氣候事件的特征，而且在一定程度上更能揭示某些復雜的極端事件產生的原因。

1 數據的選取及處理方法

1.1 降水指標量的選取及時頻變化特征

1.1.1 降水指標量的選取 由于本文所做的研究是汛期強降水事件的模擬，所以文中涉及各站每年5～9月降水量總和（單位：mm/a）；各站每年汛期降水日數（單位：d）；過程雨量是指每個降水過程的總雨量（單位：mm/過程）；強降水雨量是指發生極端降水事件時，該站點該日的降水量（單位：mm/d），強降水事件定義如下：首先，我們定義了各測站極端強降水事件的閾值[8]。具體方法是：將各站建站以來≥0.1mm的逐日日降水序列的第95個百分位值求出，該值即為極端降水事件的閾值。當某站日降水量超過了該站極端降水事件的閾值時，就稱該日出現了極端降水事件，記該站發生極端降水事件一次。在降水量相同的情況下，臺站的閾值越大，意味著越難發生極端強降水事件。通過計算，亳州地區強降水事件的閾值在36.6～40.5mm/d變化，平均閾值為38.2mm/d。閾值均小于50mm，這說明國家氣象局定義的暴雨（50～100mm/d）事件對于研究亳州的強降水事件是不太符合的。所以在下文研究二維Gumbel分布模型時，可以把強降水雨量而非暴雨雨量做為其中的一個指標。

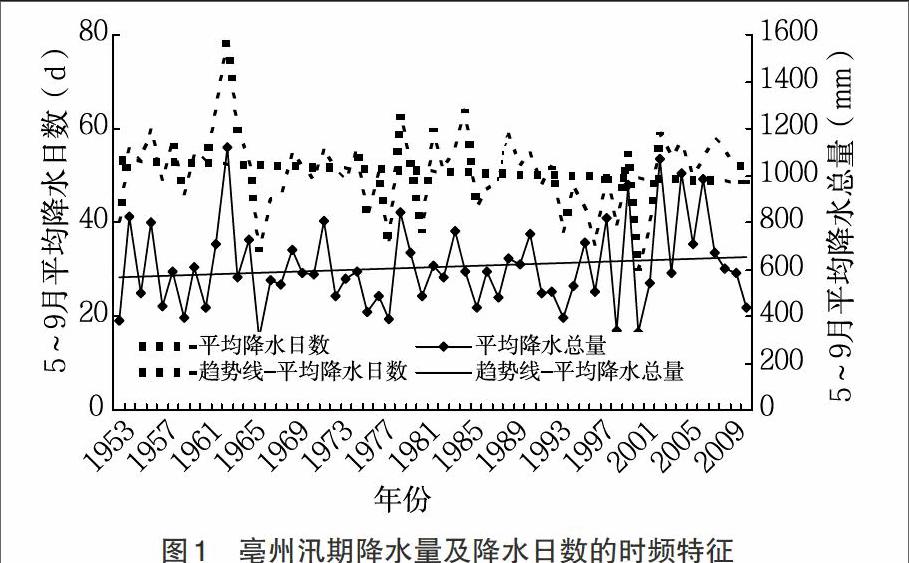
1.1.2 汛期降水量及降水日數的時頻特征 圖1是亳州4個站平均汛期降水量和降水日數隨時間的變化。從圖1可以看出，亳州汛期降水量雖然呈波動變化，但是總體上表現為增加趨勢。其多年平均汛期降水量在306～

1 120mm波動，最小值出現在1966年，為306.9mm；最大值發生在1963年，達1 118.3mm，最大值與最小值相差約810mm。汛期降水日數趨勢線表明，整體而言，亳州的降水日有減少趨勢，自20世紀80年代中期后，降水日數的減少趨勢更加明顯。亳州汛期降水量豐富，近50a來汛期降水呈增加趨勢，其降水日卻以-0.77d/10a的速度在減少。由此可見，近50a來亳州地區的降水強度必然有所增大。

圖1 亳州汛期降水量及降水日數的時頻特征

1.2 數據處理方法 由給定的逐日降水樣本序列如何估計其極值分布參數，本文采用的是經典矩估計法。首先要對逐日資料作抽取極值的資料處理，以便組成極值序列（通常稱其為有序樣本序列），文中采用部分歷時序列法（PDS）對降水資料進行抽樣。并按以下二維Gumbel分布函數公式：

[F（x，y）=exp-（-lnF（x））m+（-lnF（y））m1m，（m≥1）] （1）

計算得出相應的理論累積頻率[F（x，y）]。并計算兩者的相關系數及關聯指數，再由兩變量各自的標準化變量便可求得各自的邊際分布函數。同理，假定[X≤x]，或[Y≤y]則可分別求得[y]的條件累積分布函數和[x]的條件累積分布函數，由此又可得到相應的各不同條件下的過程雨量或強降水雨量的重現期。

值得指出的是，為了確定經驗的聯合累積頻率函數，參照Yue（2001）所采用的確定經驗累積頻率的方法，本文采用如下的公式：

[pkl=P（X≤xk，Y≤yl）=（k+l）2（N+1）] （2）

上式中，參數[k]和[l]分別為相應的變量[x，y]各自的序號，而[N]則為樣本總容量即序列長度。之所以考慮這一公式，是因為兩變量出現極值并非完全同步，有的年份出現強降水極大值，但未必過程雨量也是最大值。此外，根據前述的參數估計方法所得到的理論累積頻率（即聯合累積概率），就可在此基礎上，作二維分布的擬合優度K-S檢驗，并估計其聯合重現期。

2 描述逐日強降水概率特征的資料基礎

強降水過程是由多次暴雨雨峰所組成的，在降水過程間隙雨量較少，因此，較為完整地描述一次強降水過程必然包含2種指標：總雨量和雨峰雨量。本文利用逐日降水資料中的過程降水量及最大強降水雨量來近似地描述其極值概率特征（即強降水概率特征）。選取亳州區域內4個站汛期的逐日降水過程來定義強降水極端天氣氣候事件，采用過程降水量和其間的最大強降水雨量這2個量同時達到全年最大值作為二維分布的基本資料。經計算可以得出4站強降水雨量和過程雨量的平均值和標準差以及Gumbel分布參數，其值列于表1。

為了解Gumbel分布的擬合優度，分別對強降水雨量和過程雨量的分布進行了K-S檢驗，檢驗結果見表2。檢驗結果表明，4站的強降水雨量K-S檢驗統計值分布在0.05～0.09，過程雨量K-S檢驗統計值分布在0.09～0.15，K-S檢驗中[λ0.05]臨界值為0.19。因此，4站的強降水雨量以及過程雨量在[0.05]顯著性水平上都符合各自的一維Gumbel分布。

3 結果與分析

3.1 聯合分布 由前文所提方法，根據科爾莫哥洛夫-斯米爾洛夫（K-S）檢驗，首先可計算得到一維Gumbel分布函數[F（x）]和經驗頻率函數[f（x）]，二維Gumbel分布函數，以及二維Gumbel分布的條件分布函數[F（xy）]和[F（yx）]。應用有序樣本，計算各站各相應序列的K-S統計量，如表3所示：

在各站汛期逐日強降水過程中，過程雨量和強降水雨量各自均符合Gumbel分布，計算還表明，過程雨量和強降水雨量的聯合分布也都符合二維Gumbel分布，經K-S檢驗，它們的擬合優度都在0.05顯著性水平上符合二維Gumbel分布，檢驗結果見表3。圖3為亳州、渦陽、蒙城、利辛4站的聯合分布函數曲線與實測累積頻率曲線對比。由圖3可知，亳州地區內的4個站的強降水雨量以及過程雨量都符合聯合二維Gumbel分布，強降水雨量以及過程雨量的聯合分布函數曲線與實測累積頻率曲線擬合效果較好。通過聯合分布函數的計算，可以得出亳州地區強降水雨量及過程雨量的聯合重現期。

<3.2 條件分布（累積條件分布函數） 根據前文給出的條件分布概率函數，可以求得各種不同前提條件（如不同強降水雨量）下的過程總雨量的條件分布函數及其相應重現期和分位數。以亳州汛期為例，圖4為亳州強降水雨量（上）和過程總雨量（下）條件重現期列線。

由圖4可知，當強降水雨量一定時，過程雨量越大，其條件重現期越長；過程雨量一定時，強降水雨量越大，條件重現期越長。以亳州為例，當出現50mm強降水時，條件概率為0.724 3，其過程雨量約為71.9，重現期為1.2a；當出現100mm強降水時，條件概率為0.214 9，其對應過程雨量為181.4mm，重現期為5a。為了更好的對比說明，表4分別列出了亳州、齊齊哈爾、廣州3站的過程降水在強降水雨量分別為50mm和100mm條件下的條件概率、分位數。由表4可知，由北往南，過程的降水強度是逐漸增加的，在同級強降水雨量出現的條件下，過程降雨量愈往南方其條件概率愈大，而其出現的過程雨量也隨之增大，這是符合氣候實際的。而且條件重現期由北往南是逐漸減少的，從數據可見，廣州每年的強降水雨量最大值幾乎都超過50mm，其重現期相比齊齊哈爾、亳州而言更短。而在強降水雨量最大值超過100mm時，齊齊哈爾的條件概率僅為0.01，也就是說，其重現期要100a，這種情況是百年一遇的，亳州相比而言，超過概率為0.2，其重現期為5a，但是到了雨水充沛的廣州，其條件概率竟達0.51，且其重現期為2a。可見，條件概率之間的差異不如過程雨量之間的差異來得大，強降水雨量為50mm時的條件概率遠比100mm時的條件概率大，在條件重現期上體現的更加明顯。

4 結論

選取亳州4個站點建站以來汛期的逐日降水數據進行二維Gumbel分布模式研究，得出以下結論：

（1）采用亳州4個測站的逐日降水資料，運用PDS方法進行數據的抽樣，選用經典矩估計方法進行參數的計算，然后進行Gumbel分布的擬合，結果表明所選描述強降水過程的氣象要素均符合該分布，且計算簡單、效果穩定。

（2）利用二維Gumbel分布模式進行汛期單站點強降水特征模擬，經用K-S檢驗，表明二維Gumbel分布對汛期極值概率分布有著很好的擬合效果，并可模擬得出單站點的聯合分布概率及聯合重現期、條件分布概率及條件重現期。

（3）汛期降水極值統計的根本目的在于利用已知的分布模式推算極值的重現期，即某一極值再次出現的時間間隔，重現期的計算能為當地提供農業氣象災害的預警信息，而且本模式也能推廣到對干旱重現期的研究中，這對于防災減災、保障人民經濟生活都有著重要的意義。

參考文獻

[1]么枕生，丁裕國.氣候統計[M].北京：氣象出版社，1990：161-256.

[2]程炳巖，丁裕國，李云.中國日降水量與其占有面積的函數關系[J].高原氣象，2005，24（3）：422-427.

[3]丁裕國，江志紅.極端氣候研究方法導論[M].北京：氣象出版社，2009：79-150.

[4]Gumbel E J.Multivariate extremal distributions[J].Bull Int Stat Inst，1960，39（2）：471-475.

[5]Gumbel E J.Bivariate logistic distributions[J].J Am Stat Assoc，1961（56）：335-349.

[6]Gumbel E J，Musta CK.Some analytical properties of bivariate extreme distributions[J].J Am Stat Assoc，1967（62）：569-588.

[7]Guo S L.A discussion on unbiased plotting positions for the general extreme value distribution[J].J Hydrol，1990（212）：33-44.

[8]Wang Q J.The POT model described by the generalized Pareto distribution with Poisson arrival rate[J].J Hydrol，1991（129）：263-280. （責編：張宏民）