飽和多孔彈性桿熱傳導的廣義多辛方法及其數值實現
?
飽和多孔彈性桿熱傳導的廣義多辛方法及其數值實現
劉雪梅1,2,鄧子辰1,胡偉鵬1
(1.西北工業大學力學與土木建筑學院,陜西西安710072; 2.長安大學工程力學系,陜西西安710064)
摘要:首先根據多孔介質理論,利用飽和多孔介質的能量方程和本構關系,推導出飽和多孔彈性桿局部熱平衡的熱傳導方程;繼而引入正交變量,將熱傳導方程導入Hamilton系統,得到飽和多孔彈性桿熱傳導方程的廣義多辛形式和多種局部守恒律形式;接著采用中點離散方法對熱傳導方程的廣義多辛形式進行數值離散;最后利用計算機數值實現了飽和多孔彈性桿的熱傳導過程,并且討論了參數取值的不同對熱傳導過程的影響,同時在數值模擬過程中記錄了廣義多辛格式的局部動量誤差。研究結果表明,構造的廣義多辛方法能夠很好地模擬系統的熱傳導過程和耗散效應,同時也可長時間保持系統的固有幾何性質。
關鍵詞:多孔介質;廣義多辛;耗散;熱傳導
飽和多孔介質通常是指孔隙中充滿液體的多孔連通介質,其相關理論在地震工程學、土動力學、地球物理學、生物力學等領域有著廣泛應用。目前,研究多孔介質宏觀力學行為的主要理論有: Biot理論、多孔介質理論和混合物理論。在Biot理論基礎上,徐曾和等研究了含單一圓井的飽和多孔地層中,以定流量方式開采時的流固耦合問題[1]; de Boer等基于多孔介質理論,研究了流固兩相微觀不可壓飽和多孔介質穩態振動的基本解[2];秦冰等以混合物理論為基礎,將非飽和土視為由土骨架、液態水、水蒸氣、干燥氣體及溶解氣體共5種組分構成的混合物,系統研究了非飽和土的熱-水-力多場耦合問題[3]。然而,有關各類飽和多孔結構熱傳導過程的數值算法研究較少,尤其是熱傳導方程的求解過程中如何體現由于熱量傳遞引起的耗散效應以及如何保持系統的局部能量守恒律和局部動量守恒律等局部幾何性質更是數值算法的難點。
1984年是應用數學和計算力學研究中具有重要意義的一年,也是辛幾何算法開創性發展的一年,我國數學家馮康于這一年首次系統地提出了哈密頓方程和哈密頓算法,并指出了從辛幾何內部系統構成算法并研究其性質的途徑,從而開創了辛幾何算法的新領域[4]。自此以后,辛幾何算法得到了長足的發展,學術界將純理論的辛幾何和現代科學工程計算有機地結合起來,使其廣泛地應用于天體動力學和分子動力學等諸多領域[5]。在此基礎上,Bridge教授針對無窮維Hamilton系統提出了多辛算法[6],用以在數值求解過程中保持系統的局部幾何性質。然而,實際力學系統中耗散效應的存在卻成了多辛算法的“瓶頸”,近年來,廣義多辛算法理論的提出[7-9],有效地解決了這一"瓶頸"問題,將保結構算法理論體系拓寬至耗散系統。
多孔介質傳熱現象遍及于工農業生產的各個領域,例如:埋地電纜和直流接地極的熱耗散;地源熱泵和地冷空調中換熱器埋管;高溫原件的多孔冷卻;生物多孔介質的傳熱問題等等。因此,多孔介質傳熱理論和應用研究是一個具有重要學術和應用價值的研究方向,而作為多孔介質一維傳熱問題中最基礎的飽和多孔彈性桿的熱傳導就更加重要,它的研究將為多孔介質桿系結構以及植物根莖等多種多孔介質結構的傳熱傳質問題提供有力的依據,尤其是其數值求解的應用將更加廣泛。正是基于這一點,本文試圖通過廣義多辛保結構算法來尋求新的研究飽和多孔彈性桿熱傳導過程的數值方法,同時也為了揭示其熱傳導過程中的耗散效應以及系統的廣義多辛守恒律等多種局部幾何性質,從而為多孔介質傳熱問題的數值求解提供新的途徑。
本文基于飽和多孔介質理論,首先建立飽和多孔彈性桿熱傳導的一維數學模型。其次,通過正則變換,構造飽和多孔彈性桿熱傳導方程的廣義多辛形式,并研究了熱量傳遞的耗散效應在廣義多辛形式中的數學表述。隨后,采用中點離散方法離散廣義多辛形式,得到其中點Box廣義多辛離散格式。最后,利用中點Box廣義多辛離散格式數值模擬飽和多孔彈性桿的熱傳導過程,并將數值解與精確解進行比對,同時研究了熱傳導過程中的耗散效應。本文的廣義多辛分析將完善保結構算法理論,也為多孔介質耗散系統的數值求解提供新的途徑。
1 飽和多孔彈性桿的熱傳導方程
為了研究飽和多孔彈性桿的傳熱問題,本文建立如圖1的模型:設長為L、橫截面高度為H的流體飽和多孔彈性桿由不相溶的微觀不可壓流體和微觀不可壓彈性多孔固相骨架組成,其側表面不透水。根據多孔介質理論,每一相物質被理想化地分布在整個區域中,并擁有各自獨立的運動,記物質粒子的位移為:

圖1 LH的飽和多孔彈性桿
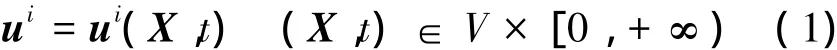
式中,i =S、F分別表示固相和流相,V為多孔介質初始時的空間區域。忽略兩相間的質量交換,則流固兩相的能量方程可表示為[10]:
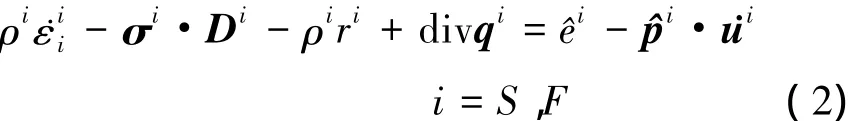
式中,ρi為兩相的宏觀質量密度;εi、σi、qi和ri分別為兩相的內能、宏觀應力張量、熱流矢量和內部熱源;i和i分別為兩相間的相互作用力和能量交換量,滿足+= 0+= 0; ()i=+ grad(…)·i表示隨物相的物質時間導數。
對于各向同性線彈性多孔固相骨架和無粘性流體,在兩相不可壓和小變形的假定下,并忽略由于流固兩相的相對運動引起的附加熱對流和附加熱傳導,可得流固兩相的宏觀應變張量和宏觀應變率張量分別為:
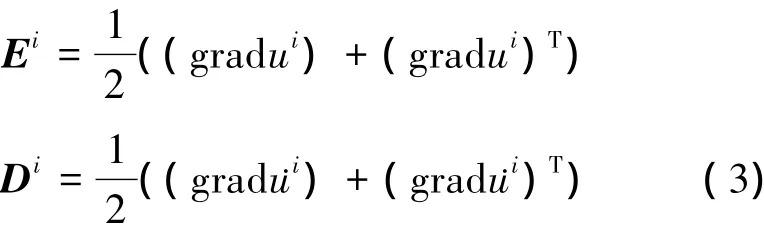
本構方程可表示為[10]:
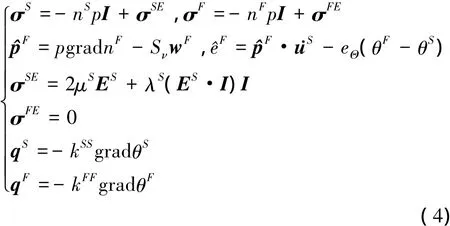
式中,上標T表示轉置,p和Sν分別表示有效孔隙水壓力和與流體滲流系數有關的兩相相互作用耦合系數,eΘ為非局部熱平衡引起的兩相間能量交換系數,μS和λS為固相宏觀拉梅常數,kii和θi(i = S,F)分別為熱傳導系數和流固兩相的溫度,wF=F-S為孔隙流體相對固相骨架的速度。
以下考慮局部熱平衡情況,即在每一個空間點上,固相骨架和孔隙流體具有相同的溫度,其溫度可表示為θS=θF=θ,將(3)式和(4)式代入能量方程(2)中,并采用如圖1所示的一維空間坐標軸,同時忽略非線性項對熱傳導的影響[10],可得飽和多孔彈性桿局部熱平衡時的熱傳導方程:
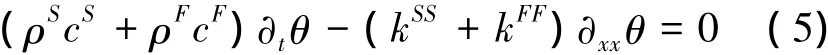
式中,θ和ci(i = S,F)分別表示局部熱平衡溫度和流固兩相的比熱容,再引入如下無量綱量和常量:
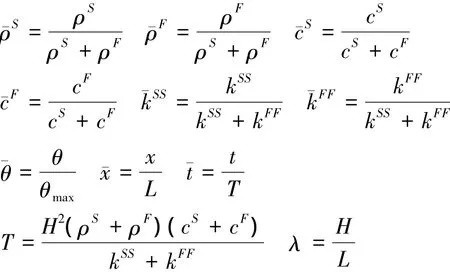

2 飽和多孔彈性桿熱傳導方程的廣義多辛形式
對于飽和多孔彈性桿熱傳導方程(6),引入正交變量φ=?xθ,上述二階偏微分方程(6)可轉化為以下一階耦合Hamilton方程組形式:
M?tz + K?xz =▽zS(z),z =[θ,φ]T∈R2(7)
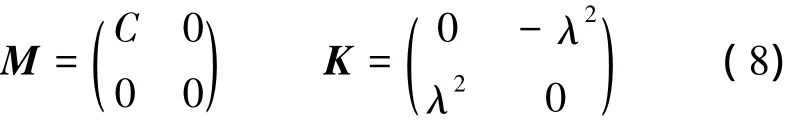
從(8)式容易看到,系數矩陣M并不是反對稱的,因此,按照廣義多辛算法的概念[8],(7)式為廣義多辛形式。這是由于本文涉及的飽和多孔彈性桿的熱傳導問題中存在著熱量傳遞,從而使系數矩陣M并不是反對稱的,也正是由于非完全反對稱矩陣的存在,上述廣義多辛形式(7)式就不能滿足多辛算法的多辛守恒律和局部動量守恒律。
基于多辛理論,由多辛守恒律概念可給出廣義多辛形式(7)式的廣義多辛守恒律為[8]:
同時,由局部動量守恒律誤差的概念,亦可給出廣義多辛形式(7)式的局部動量守恒律誤差為:
這里需要指出,由于系數矩陣K是嚴格反對稱的,廣義多辛形式(7)式嚴格滿足局部能量守恒律。
3 飽和多孔彈性桿熱傳導方程的廣義多辛離散
本文選用中點差分離散方法分別在空間方向和時間方向對廣義多辛形式(7)式進行差分離散,并分別選取時間步長Δt和空間步長Δx對計算區域均勻劃分,用zji表示狀態變量z在(xi,tj)網格點上的近似值,則可得時間和空間2個方向上的中點Box離散格式:
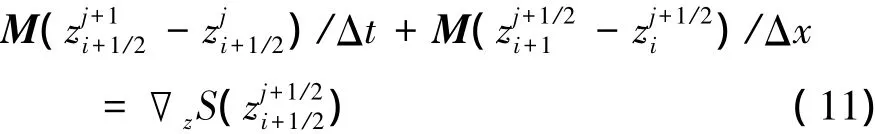
式中
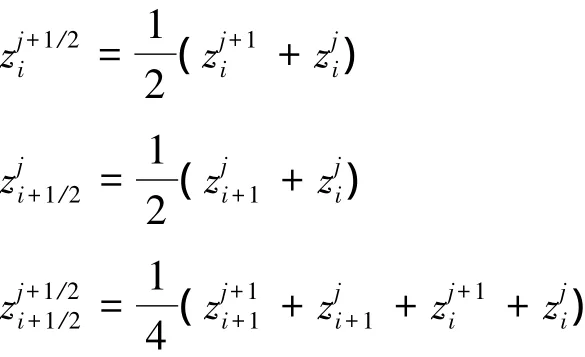
將系數矩陣(8)和狀態變量z =[θ,φ]T以及Hamilton函數代入上述離散格式(11),便可得到廣義多辛偏微分方程(7)的等價形式:
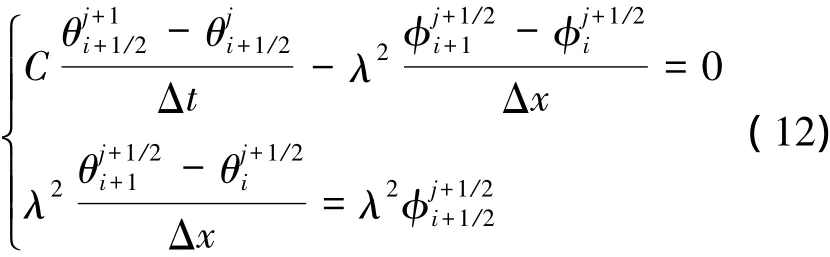
對于上述已得到的廣義多辛守恒律(9)式,亦可通過有限差分運算得到其離散格式。這里采用向前差分運算,得到廣義多辛局部動量誤差的離散形式[7]:
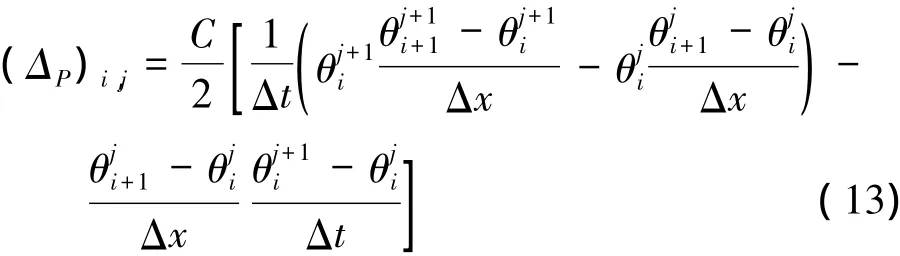
為了得到局部動量誤差隨時間變化的平面圖,本文取廣義多辛局部動量誤差在第j時間步的絕對值[7]:

4 數值實驗
這一節中,本文將利用以下飽和多孔彈性懸臂桿的數值算例來探討和驗證前述已構造出的廣義多辛離散格式的精確性、有效性和數值穩定性等性能。
在廣義多辛離散格式(12)中,考慮如下邊界條件和初始條件:
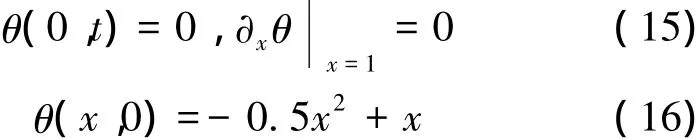
選取計算空間步長Δx = 0. 01,時間步長Δt =0. 5,λ2= 0. 000 1,分別取參數C = 0. 043和C = 0. 02,在t∈[0,200]內,得到局部熱平衡時飽和多孔彈性桿不同時刻的溫度隨空間坐標的變化圖(見圖2和圖3)。為了驗證廣義多辛離散格式(12)的精確性,采用分離變量法,可得無量綱偏微分方程(6)的定解問題(15)~(16)的精確解:
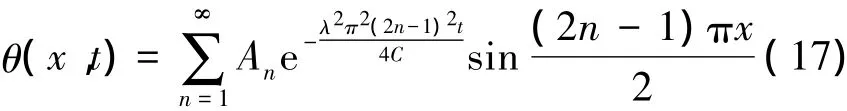
式中
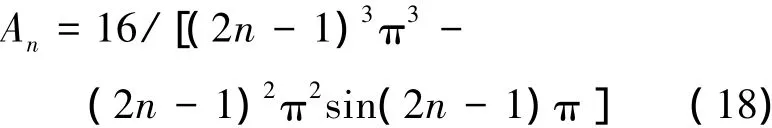
因此,亦可得局部熱平衡時飽和多孔彈性桿不同時刻溫度場的精確解隨空間坐標的變化圖(圖2和圖3)。

圖2 C=0. 043時不同時刻溫度的數值解(點)與精確解(曲線)的比較
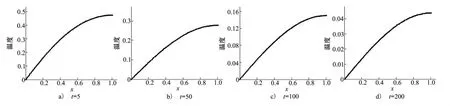
圖3 C=0. 02時不同時刻溫度的數值解(點)與精確解(曲線)的比較
圖2反映了參數C = 0. 043時飽和多孔彈性桿局部熱平衡的熱傳導過程,這一過程中,由于桿x = 1端與外界絕熱,初始溫度從桿x = 1端向桿x = 0端逐漸降低,因此隨著時間的推移,熱量將從桿x = 1端向桿x = 0端廣泛傳遞,從初始時刻到t = 200的過程中,桿x = 1端的溫度從0. 5降低至0. 16;熱傳導過程中,由于桿內部無熱源,桿x = 0端溫度始終為零,桿將由x = 0端持續向外界傳熱,桿內各點的溫度均逐漸下降。與圖2類似,圖3反映了參數C = 0. 02時飽和多孔彈性桿局部熱平衡的熱傳導過程,這一過程中明顯可以看到,相同時刻桿內各點的溫度均比C = 0. 043時低,t = 200時,桿內各點溫度均已接近零;由此可以說明,參數C的取值越小,熱傳導過程將越快;這種現象是因為參數C取值的減小,相當于飽和多孔彈性桿熱傳導方程的導熱系數增大,則必然導致熱傳導過程加快。此外,由圖2和圖3均可看到,熱傳導過程中溫度場分布的數值解與精確解非常吻合。以上這些結果說明本文采用的廣義多辛方法具有很好的有效性和精確性。
為了進一步驗證廣義多辛格式(12)的局部保結構性,本文將無量綱模擬時間延長至500,利用(14)式,將第j時間步中誤差絕對值最大的空間點的數值誤差作為該時間步的局部動量數值誤差,并取參數C足夠小(其中C分別取0. 01和0. 043) ;繼而在計算機模擬過程中記錄每一時間步的局部動量誤差,從而得到廣義多辛局部動量數值誤差隨時間的變化曲線圖(見圖4)。
從局部動量數值誤差的結果可以看出:整個模擬過程中,局部動量誤差均在10-5數量級以下,這說明本文構造的廣義多辛算法能夠很好地模擬系統的熱量傳遞耗散效應,并且保持了系統的固有幾何性質。從圖4可以看到,參數C取0. 043時,無量綱時間從t = 450之后,局部動量誤差為零;然而參數C取0. 01時,無量綱時間從t = 100之后,局部動量誤差就已經為零。這就是說,參數C的取值越小,局部動量誤差將越早等于零,這也就表示,參數C的取值越小,越能體現本文構造的廣義多辛形式的局部保結構性。

圖4 不同參數C下的局部動量數值誤差
5 結論
本文首先基于多孔介質理論,通過多孔介質能量方程和本構關系,首先推導出飽和多孔彈性桿局部熱平衡時的熱傳導方程;繼而在多辛算法理論的基礎上,采用廣義多辛算法研究了這一熱傳導問題,構造出飽和多孔彈性桿局部熱平衡時熱傳導方程的廣義多辛形式和廣義多辛守恒律以及廣義多辛局部動量守恒律誤差,并且得到其相應的中點Box廣義多辛離散形式;最后,在已得的離散格式的基礎上,數值考察了飽和多孔彈性桿局部熱平衡時的熱傳導過程,將溫度場的數值結果與精確解進行比較,并且數值考察了一段長時間內的局部動量誤差。得到如下結論:
1)本文構造的廣義多辛格式能夠很好地模擬飽和多孔彈性桿的熱傳導過程,數值實現了熱傳導過程中溫度場隨時間的變化,并且數值解與精確解非常吻合,這充分顯示出本文采用的廣義多辛方法具有很好的有效性和精確性;
2)在局部動量數值誤差的研究中,本文選取了不同的參數,均得到數量級在10-5以下的誤差結果,這表明本文構造的廣義多辛格式能夠很好地保持系統的固有幾何性質,并且具有良好的長時間數值穩定性。
參考文獻:
[1]徐曾和,徐小荷.飽和多孔地層中定量抽放的流固耦合問題[J].巖土工程學報,1999,21: 737-741 Xu Zenghe,Xu Xiaohe.Fluid-Solid Coupling Problem in the Liquid Extraction at Fixed Flux[J].Chinese Journal of Geotechnical Engineering,1999,21: 737-741 (in Chinese)
[2]De Boer R,Svanadze M.Fundamental Solution of the System of Equations of Steady Oscillations in the Theory of Fluid-Saturated Porous Media[J].Transport in Porous Media,2004,56: 39-50
[3]秦冰,陳正漢,方振東,孫樹國,方祥位,王駒.基于混合物理論的非飽和土的熱-水-力耦合分析模型Ⅰ[J].應用數學與力學,2010,31: 1476-1488 Qin Bing,Chen Zhenghan,Fang Zhendong,Sun Shuguo,Fang Xiangwei,Wang Ju.Analysis of Coupled Thermo-Hydro-Mechanical Behavior of Unsaturated Soils Based on Theory of MixturesⅠ[J].Applied Mathematics and Mechanics,2010,31: 1476-1488 (in Chinese)
[4]Feng K.On Difference Schemes and Symplectic Geometry[C]∥Proceeding of the 1984 Beijing Symposium on D D,1984: 42-58
[5]趙長印,廖新浩,劉林.辛算法在動力天文中的應用[J].計算物理,1992,4: 812-812 Zhao Changyin,Liao Xinhao,Liu Ling.Application of Symplectic Algorithm in Dynamic Astronomy[J].Chinese Journal of Computational Physics,1992,9(4) : 812-812 (in Chinese)
[6]Bridge T J.Multi-Symplectic Structures and Wave Propagation[J].Mathematical Proceedings of the Cambridge Philosophical Society,1997,121: 147-190
[7]Hu W P,Han S M,Deng Z C,Fan W.Analyzing Dynamic Response of Non-Homogeneous String Fixed at Both Ends[J].International Journal of Non-Linear Mechanics,2012,47: 1111-1115
[8]Hu W P,Deng Z C,Han S M,Zhang W R.Generalized Multi-Sympletic Integrators for a Class of Hamiltonian Nonlinear Wave PDEs[J].Journal of Computational Physics,2013,235: 394-406
[9]胡偉鵬,鄧子辰.大阻尼桿振動的廣義多辛算法[J].動力學與控制學報,2013,11: 1-4 Hu Weipeng,Deng Zichen.Generalized Multi-Sympletic Method for Vibration of Big Damping Rod[J].Journal of Dynamics and Control,2013,11: 1-4 (in Chinese)
[10]Yang X.Gurtin-Type Variational Principles for Dynamics of a Non-Local Thermal Equilibrium Saturated Porous Medium[J].Acta Mechanica Solida Sinica,2005,18: 37-45
[11]楊驍,程昌鈞.流體飽和多孔介質的動力學Gurtin型變分原理和有限元模擬[J].固體力學學報,2003,24: 267-276 Yang Xiao,Cheng Changjun.Gurtin Variational Principle and Finite Element Simulation for Dynamical Problems of Fluid-Saturated Porous Media[J].Acta Mechanica Solida Sinica,2003,24: 267-276 (in Chinese)
Generalized Multi-Symplectic Method and Numerical Experiment for Thermal Conduction of Saturated Poroelastic Rod
Liu Xuemei1,2,Deng Zichen1,Hu Weipeng1
(1.Department of Engineering Mechanics,Northwestern Polytechnical University,Xi'an 710072,China 2.Department of Engineering Mechanics,Chang'an University,Xi'an 710064,China)
Abstract:Based on the theory of porous media,the thermal conduction equation of fluid saturated poroelastic rod is established by using the energy equation and constitutive relations of the two constitutes firstly in this paper.Then introducing orthogonal variables,we use the generalized multi-symplectic method to derive a first-order generalized multi-symplectic form for thermal conduction equation and several errors of conservation laws illustrating the local properties of the system.Thirdly,a midpoint box generalized multi-symplectic scheme is constructed; furthermore,discrete errors of generalized multi-symplectic conservation law and generalized local momentum conservation law are also obtained.Finally,the dissipation effect in thermal conduction process of saturated poroelastic rod and generalized local momentum conversation law are investigated numerically; moreover,the influence of parameter values for thermal conduction process is established later.From results of the numerical experiments,it can be preliminarily concluded that the generalized multi-symplectic scheme constructed in this paper has excellent accuracy,longtime numerical behavior and good conservation properties.
Key words:boundary conditions,constitutive equations,errors,matrix model,momentum,numerical methods,porosity,temperature distribution,thermal conductivity; dissipation,generalized multi-symplectic,saturated poroelastic rod,thermal conduction
作者簡介:劉雪梅(1980—),女,西北工業大學博士研究生,主要從事多孔介質問題的保結構算法研究。
收稿日期:2014-09-10基金項目:國家自然科學基金(11372252、11172239和11372253)與中央高校基金(2014G1121096)資助
文章編號:1000-2758(2015) 02-0265-06
文獻標志碼:A
中圖分類號:O241.82

