一種基于交叉熵的黑白棋盤角點檢測算法

?

一種基于交叉熵的黑白棋盤角點檢測算法

趙斌1，2，J．Guo2，E．K．A．Gill2，周軍1

(1．西北工業大學精確制導與控制研究所，陜西西安710072 2．Faculty of Aerospace Engineering，Delft University of Technology，Kluyverweg 1，2629 HS Delft，The Netherlands)

摘要:分析了現有黑白棋盤角點檢測算法存在的不足，將交叉熵思想引入角點檢測中。該算法首先將角點周圍像素劃分為4個象限，通過相鄰象限間的像素灰度差實現角點初選;其次，給出對角象限灰度交叉熵定義，根據局部交叉熵最小原理實現角點篩選;第3，針對備選角點局部重疊的問題，采用梯度幅值非極大值抑制方法實現像素級角點定位;最后采用Frostner算子實現角點的亞像素坐標解算。實驗結果顯示該算法檢測結果優于經典Harris算子以及SV算子，獲取的角點亞像素坐標精度與Matlab相機標定工具箱相當，同時易于實現在線標定。

關鍵詞:相機標定;棋盤角點檢測;交叉熵;非極大值抑制;梯度幅值

在室內衛星編隊飛行平臺［1-2］中，視覺系統的標定精度是確保漂浮體定位精度的關鍵，其通常包括圖像特征點檢測和相機參數求解2個過程。關于相機參數求解，張正友算法［3］已經比較成熟，而圖像特征點檢測則成為研究熱點。

第1類方法多采用黑白棋盤標定模板，對此實現角點檢測最早的方法是Harris算法［4］，采用局部灰度值的高斯梯度實現角點檢測，當角點周圍存在圖像模糊時會得到多個虛假角點，影響標定精度。文獻［5］采用2次Hough變換實現黑白柵格直線擬合，并根據直線交點獲取角點精確坐標。文獻［6］采用旋轉直角模板進行角點篩選，然后采用多次曲線擬合實現角點確定。這2種方法計算量大，難以實現在線標定。文獻［7］提出對稱方差檢測算法(SV算子)，該方法僅采用角點附近2個象限的像素信息，實際使用中會產生錯誤角點。文獻［8］提出一種改進的SV檢測算子，采用平面到平面的變換實現角點初定位，基于區域能量中心概念實現精確定位。其仿真結果表明，該算法會造成部分角點丟失。文獻［9］通過Radon變換和黑白檢測算子檢測4個典型特征方向上像素灰度分布特征實現角點檢測，當圖像邊緣存在畸變時其檢測性能得不到保證。文獻［10］采用Hessian矩陣算子進行角點初選，然后基于對稱約束確定真實角點，該方法采用圓形檢測模板使得有用像素總有一部分處于扇形邊緣，這會造成有用信息流失，進而影響檢測精度。

第2類方法采用新的標定模板進行特征點檢測。文獻［11］在黑白棋盤四周增加了4條長寬比較大的長方形邊界，基于參考圖像和腐蝕算子檢測長方形邊界，在此基礎上采用交比不變性原理實現角點定位。文獻［12］在黑白棋盤中增加了5個沙漏狀的圖形，充分減小了立體投影后圖像幾何形狀變化的影響。文獻［13］提出一種以漸進圓形為特征的標定模板及相應的檢測算法，結果顯示標定精度相比黑白棋盤提高20%。這些方法多次采用曲線擬合計算量較大，此外其標定模板也僅適用于具體的應用。

第3類方法是采用現有的軟件工具箱直接進行相機標定，使用較廣泛的有2種: Matlab相機標定工具箱［14］和OpenCV算法庫［15］。前者在使用過程中需要用戶人工選擇4個邊界角點，無法實現自動標定，而且該工具箱不支持處理大于2Mb的圖像［6，11］。從實驗結果看，OpenCV算法庫實現的標定精度不如Matlab標定工具箱，并且其角點檢測結果往往排序混亂，對于參數求解不利。

基于此，本文在分析黑白棋盤角點特性基礎上，提出一種基于交叉熵的角點檢測算法。該算法原理簡單、易于實現并且可用于自動標定。對比實驗結果證明了算法的有效性和實用性。

1　棋盤角點特性分析

典型黑白棋盤標定模板如圖1所示。定義棋盤格內部角點為: 2個相間的黑色方格和白色方格的交叉點。定義像素點的四象限如圖2所示。對比其他像素點，內部角點具有如下的特性:

1)角點相鄰象限像素的灰度差絕對值最大。

2)角點對角象限像素的灰度差異最大;

3)角點局部灰度值變化劇烈，具有最大的灰度梯度值。

圖1　標準黑白棋盤標定模板

圖2　內部角點局部象限定義

2　角點檢測算法描述

如圖3所示本文提出的交叉熵檢測算法包括4個步驟:角點初定位，交叉熵篩選，局部非極大值抑制及亞像素坐標解算。其主要特點是在傳統角點初選基礎上引入象限灰度信息距離實現精確篩選。

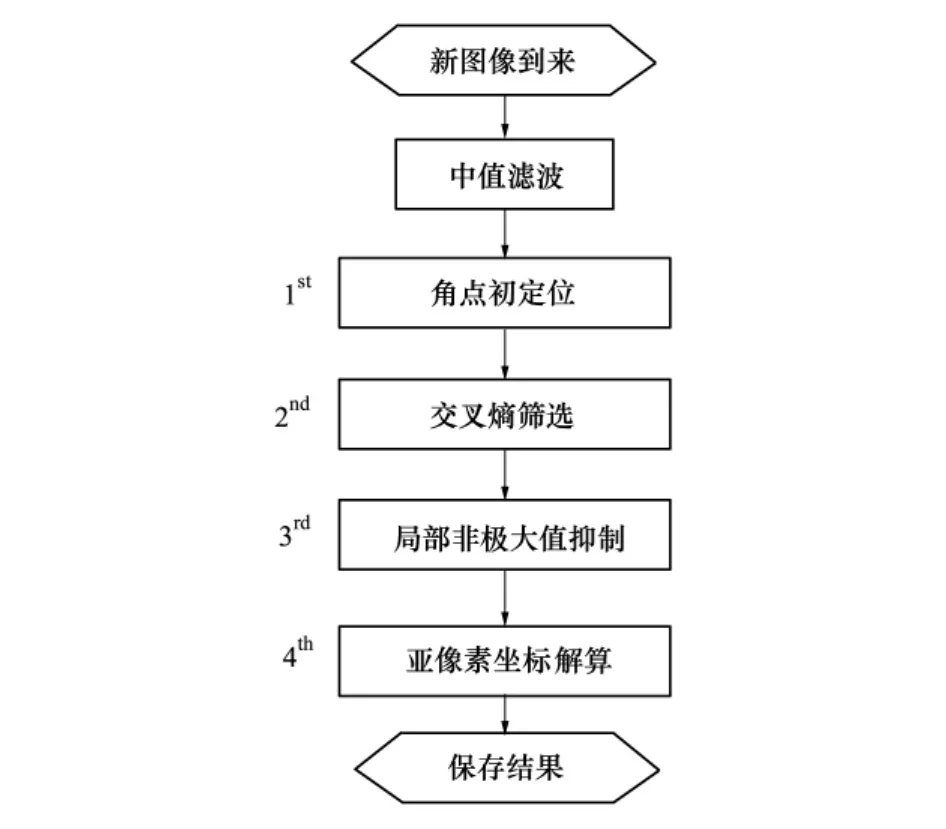
圖3　交叉熵檢測算法流程

2. 1角點初定位

根據上文特性1，定義角點鄰域正方形滑動窗W，邊長l = 2s + 1，s為分布到每個象限的正方形區域邊長。據此對4個象限像素灰度和計算如下:

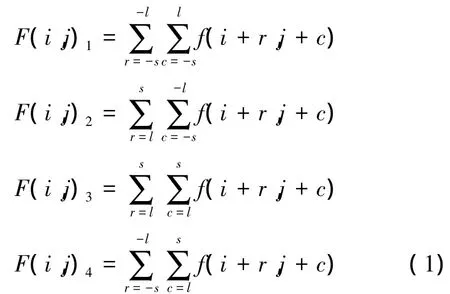
式中: f(i，j)為像素點(i，j)的灰度值，F(i，j)k是第k個象限的像素灰度和，k∈{ 1，2，3，4}。

理想情況下，圖2中黑白相鄰象限中像素灰度差絕對值為255s2。考慮到傾斜投影及采樣噪聲，灰度差通常小于該值。故得到角點初選規則如下:

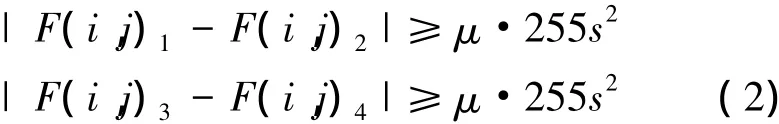
式中:μ表征相鄰像素象限灰度值差異程度，s表征檢測窗尺寸。隨著μ減小，角點檢測數量呈非線性增長，根據經驗取值0. 1～0. 3; s可以根據圖像尺寸及黑白棋盤像素面積確定，通常取值為5即可。

2. 2交叉熵篩選規則

隨機分布的交叉熵［16］表征了其信息差異的定量描述。對于角點(i，j)，可以得到先驗公式如下:

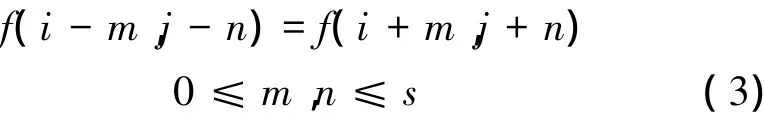
即小范圍內相對角點(i，j)對稱的像素點灰度值也對稱。由此可知互相對稱的2個象限之間灰度差異最小，可以給出兩者交叉熵定義如下。

定義1針對角點(i，j)，其第1象限和第3象限像素灰度交叉熵可表示為:

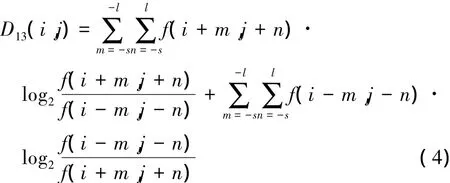
同理可得第二和第四象限灰度交叉熵D24(i，j)。

其中s同樣取值為5。對于候選角點進行交叉熵計算，對應象限灰度值對稱特性最好時，即可實現角點篩選，相關實驗結果見第3節。

2. 3局部梯度幅值非極大值抑制

為避免在模糊角點附近產生多個候選角點(如圖4c)所示)，這里引入邊緣檢測思想進行角點精確定位。通常真實的角點始終處于圖像黑白框的邊緣，采用Canny［17］算子設計非極大值抑制規則如下:

1)計算備選角點附近x與y向的灰度梯度［18］;

2)根據梯度值計算梯度向量幅值;

3)局部梯度幅值最大點即為最終的角點像素。

2. 4亞像素角點坐標解算

室內衛星編隊飛行要求視覺定位精度達到毫米級［2］，因此相機標定精度要足夠高。在上述像素級精度基礎上，引入Forstner算子［19］實現亞像素級的角點定位。以下給出亞像素坐標計算方法:

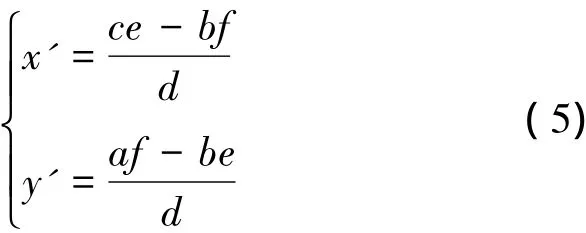
式中: (x'，y')是像素點(x，y)優化后的亞像素坐標。其中各個中間變量計算如下:

Ix與Iy分別為像素(x，y)在x及y向的灰度梯度。

3　算法測試與分析

為了對所提出的交叉熵檢測算法進行性能對比測試，選擇相機標定算法常用的標準測試圖片［14］。

3. 1算法執行結果

以圖像包中“Image 13”為例，圖4為算法的檢測結果，表1總結了前3步執行過后的角點數。

圖4　交叉熵檢測算法執行結果(Image13)

表1　交叉熵檢測算法的檢測角點數總結

如圖4a)所示，角點初選結果包括很多非角點像素;對比圖4b)可知交叉熵篩選可剔除大部分非角點像素，僅有角點附近的像素需要排除，證明了該方法的有效性;對比圖4c)說明非極大值抑制可以很好實現真實角點局部相鄰像素點的排除。

3. 2與其他算法結果對比

為了嚴格地對交叉熵檢測算法性能進行對比，選擇標準測試圖像包中“Image13”、“Image18”和“Image20”3幅圖進行實驗，這幾幅圖的拍攝傾斜角最大，產生的畸變也最大。圖5～圖7分別對比了Harris算子、SV算子以及交叉熵檢測算法之間的檢測結果，該結果同時也總結于表2中。

圖5　對比算法檢測結果

圖6　Image18檢測結果

圖7　Image20檢測結果

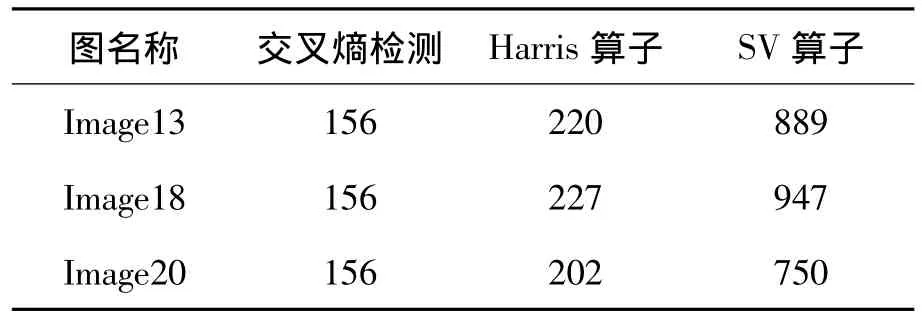
表2　幾種算法檢測結果對比

對比圖5中3種方法的檢測結果，可知交叉熵檢測算法可正確檢測出所有的內部角點，Harris算子檢測出所有角點，但是還包括非角點像素; SV算子性能最差，不但丟失了部分角點而且檢測出了大量非角點像素。由此可知:交叉熵檢測算法優于后兩者。同樣的結果可以從圖6、圖7中看出。

3. 3亞像素檢測精度分析

以“Image 13”為例，對本文算法得到的亞像素坐標值和Marlab標定工具箱得到的結果進行對比。選擇圖“Image 13”中第一行從右至左的角點坐標，對比結果列于表3中。

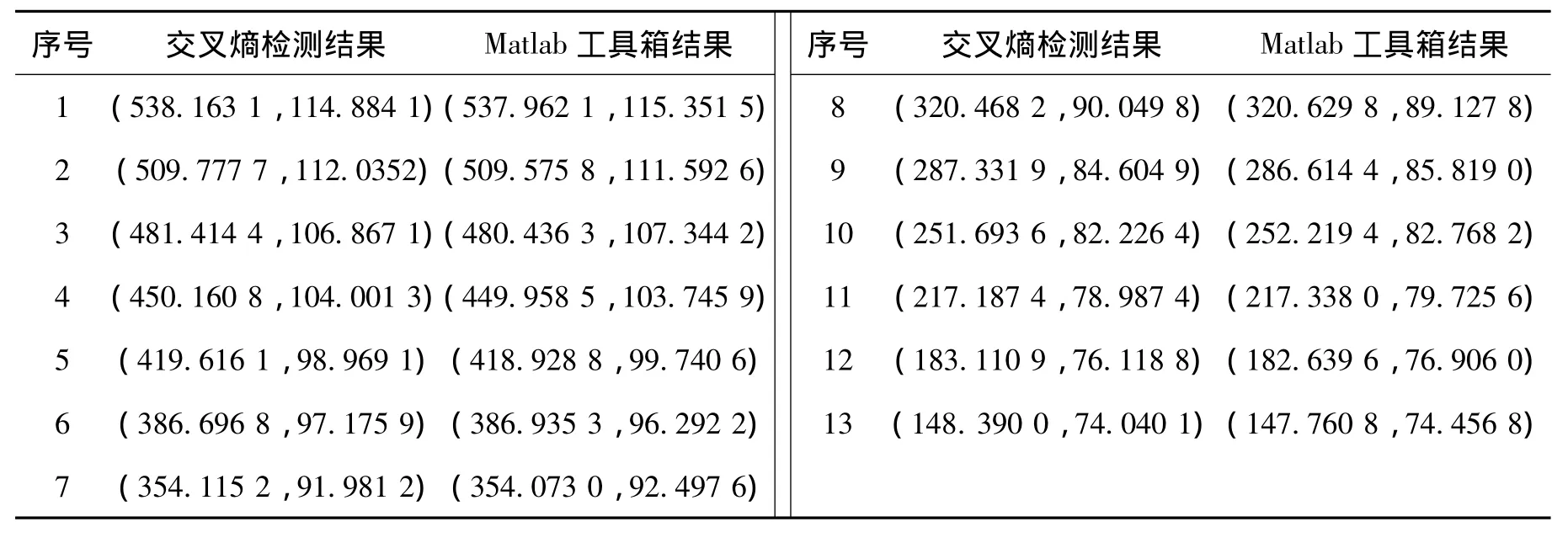
表3　亞像素坐標對比

表3顯示，2種檢測方法得到的結果相差不超過1個像素值，由此證明交叉熵檢測算法結果正確。

4　結論

本文提出一種基于交叉熵的角點檢測算法。該算法實現過程包括4個步驟:角點初選，交叉熵篩選，局部梯度非極大值抑制以及亞像素角點解算等。實驗結果顯示，該算法優于Harris算子以及SV算子，其亞像素級檢測精度與Matlab標定工具箱相當，易于實現在線標定。目前該算法已經應用于室內衛星編隊飛行平臺的視覺定位系統中，效果良好。

參考文獻:

［1］Andani Osuman．Multi-Robot Testbed for Distributed Space System［D］．Delft University of Technology，2012

［2］Zhao B，Guo J，Gill E K A．A Camera-Based Positioning System for the Formation Flying Testbed［C］∥Proceedings of the 63rd International Astronautical Congress，2012: 8325-8333

［3］Zhang Z．A Flexible New Technique for Camera Calibration［J］．IEEE Trans on Pattern Analysis and Machine Intelligence，2000，22: 1330-1334

［4］Chris Harris，Mike Stephens．A Combined Corner and Edge Detector［C］∥Proceedings of the 4th Alvey Vision Conference，Manchester，1988: l47-l51

［5］Arturo de Laescalera，Jose Maria Armingol．Automatic Chessboard Detection for Intrinsic and Extrinsic Camera Parameter Calibration［J］．Sensors，2010，10: 2027-2044

［6］Wang Zhongshi，Wu Wei，Xu Xinhe，et al．Recognition and Location of the Internal Corners of Planar Checkerboard Calibration Pattern Image［J］．Applied Mathematics and Computation，2007，185: 894-906

［7］劉陽成，朱楓．一種新的棋盤格圖像角點檢測算法［J］．中國圖像圖形學報，2006，11(5) : 656-660 Liu Yangcheng，Zhu Feng．A New Algorithm for X-Corner Detection［J］．Journal of Image and Graphics，2006，11(5) : 656-660 (in Chinese)

［8］郝穎明，朱楓．攝像機在線標定中的棋盤格角點自動檢測方法［J］．計算機工程，2007，33(17) : 213-215 Hao Yingming，Zhu Feng．Automatic X-Corners Detection for Online Camera Calibration［J］．Computer Engineering，2007，33 (17) : 213-215 (in Chinese)

［9］劉陽，王福利，常玉清，等．黑白棋盤格角點檢測算法［J］．東北大學學報，2007，28(8) : 1090-1093 Liu Yang，Wang Fuli，Chang Yuqing，et al．Black and White X-Corner Detection Algorithm［J］．Journal of Northeastern University，2007，28(8) : 1090-1093 (in Chinese)

［10］He Juan，Xia Junying，Xu Xiaoquan，et al．Automatic Corner Detection and Localization for Camera Calibration［C］∥The 10th International Conference on Electronic Measurement＆Instruments，2011: 312-315

［11］Shi Xifan，Hong Ning，Cai Tiefeng．An Automatic and Robust Chessboard Corner Extraction［J］．LNCS Transactions on Edutainment 6758，2011，49-56

［12］Yu Chunsheng，Peng Qingjin．Robust Recognition of Checkerboard Pattern for Camera Calibration［J］．Optical Engineering，2006，45: 093201

［13］梁力，尹東斐，王川．高精度攝像機標定模板的設計及識別算法［J］．西安交通大學學報，2011，45(4) : 82-85 (in Chinese) Liang Li，Yin Dongfei，Wang Chuan．Design and Detection Methods for Accurate Camera Calibration Targets［J］．Journal of Xi' an Jiaotong University，2011，45(4) : 82-85 (in Chinese)

［14］Jean-Yves Bouguet．Camera Calibration Toolbox for Matlab［EB/OL］．(2013-12-02)［2014-02-10］．http:∥www．vision．caltech．edu/bouguetj/calib-doc/index．html

［15］Gary Bradski，Adrian Kaehler: Learning Open CV［M］．USA，O'Reiuy Media，Inc，2008

［16］Li C H，Lee C K．Minimum Cross Entropy Thresholding［J］．Pattern Recognition，1993，26: 617-625

［17］John Canny．A Computational Approach to Edge Detection［J］．IEEE Trans on Pattern Analysis And Machine Intelligence，1986，8(6) : 679-698

operators，MATLAB，pixels; camera calibration，chess board corner detection，gradient amplitude，grey value difference，local overlap，non-maximum suppression，principle of minimum cross entropy

［18］Gonzalez R C，Woods R E．Digital Image Processing［M］．2nd ed，New Jersey，USA，Prentice Hall，2002

Chessboard Corner Detection Algorithm Based on Minimum Cross Entropy

Zhao Bin1，2，J．Guo2，E．K．A．Gill2，Zhou Jun1

(1．Institute of Precision Guidance and Control，Northwestern Polytechnical University，Xi'an 710072，China 2．Faculty of Aerospace Engineering，Delft University of Technology，Kluyverweg 1，2629 HS Delft，The Netherlands)

Abstract:The shortcoming of the present B/W chessboard corner detection algorithm is analyzed and a new method based on cross entropy is proposed．Firstly，the pixels around the corner are divided into 4 quadrants，and initial selection of corners is carried out based on the gray value difference between the adjacent quadrants; secondly，the cross entropy of the diagonal quadrant is defined，and the corner screening is done using the principle of minimum cross entropy; thirdly，the idea of non-maximum suppression of local gradient amplitude is introduced to solve the problem of local overlap of the candidates; at last，sub-pixel coordinates of corners are calculated using Frostner Operator．Experiments and their analysis prove preliminarily that: (1) the detection result of this algorithm is better than the classical Harris Operator and SV Operator; (2) the sub-pixel accuracy obtained is almost the same as that obtained with the Matlab Camera Calibration Toolbox，and it is suitable for online camera calibration．

Key words:algorithms，calibration，CCD cameras，entropy，flowcharting，interference suppression，mathematical

作者簡介:趙斌(1986—)，西北工業大學講師，主要從事飛行器制導控制及半實物仿真研究。

收稿日期:2014-09-18基金項目:西北工業大學基礎研究基金(JCT20130101)資助

文章編號:1000-2758(2015) 02-0216-06

文獻標志碼:A

中圖分類號:TP391．4