遺傳算法優化神經網絡的直線電機定位力辨識

（哈爾濱工業大學 航天學院，哈爾濱 150001）

電機作為一種執行元件，被廣泛應用于生產、生活的各個領域。直線電機更是憑借其相對于傳統伺服系統的高效率、高精度等優勢普遍應用于高精度運動控制系統之中。然而，電機在運轉的過程中常常受到各種擾動的影響。除了電流波紋等外界擾動之外，永磁電機由于自身機械結構和設計的局限性，難免存在磁拉力波動、齒槽力波動和邊端效應等自身擾動。在生產生活中為了實現較好的伺服控制，特別是在高精度伺服系統中，必須對這些擾動進行辨識，以進行補償而獲得更好的控制效果。以上這些波動、擾動在永磁直線電機中通常只與電機初級與次級之間的相對位置有關，統稱為直線電機的定位力。考慮到定位力辨識的必要性，文獻[1]中采用遞推最小二乘法對直線電機的定位力進行了辨識。該方法采用改進的最小二乘法，雖然一定程度上彌補了最小二乘法計算量大、實際應用性差的缺陷，但仍為一種參數化的辨識方法，其辨識精度對模型的精確程度依懶性很高，由于理論模型不能精確描述實際系統，抑或考慮到計算復雜度等方面的問題而采用簡化的數學模型，使得辨識結果存在較大誤差；文獻[2]采用了齒槽推力波動標定方法和線性插值計算方法對齒槽推力進行了建模辨識。該方法對齒槽力采樣、標定，相比之下，標定雖然方法比較簡單易懂，但操作工程量較大，而且辨識精度對插值方法依懶性比較大，如果采用插值方法不當，可能會因此造成在標定點之間的較大誤差，因而在實際應用中會有一定的局限性。考慮到以上問題與局限性，以某光刻機項目中的直線電機為例，本文提出了一種基于遺傳算法優化神經網絡的直線電機定位力辨識方法。該方法利用人工神經網絡特有的表達任意非線性映射的能力，對非線性的直線電機定位力進行辨識，并通過遺傳算法對人工神經網絡進行優化，提高算法收斂速度及辨識精度。

1 直線電機定位力特性

直線電機定位力主要是由電機齒槽力波動與邊端效應形成的，通常只與直線電機的初級和次級位置相關，因而直線電機定位力可視為一個關于直線電機位置的非線性函數。直線電機齒槽力是由直線電機定子磁場和動子鐵芯相互作用形成，齒槽力吸引動子向附近某個磁拉力平衡點移動；邊端效應是由于直線電機的開槽和動子的長度有限，磁鋼端部與電樞鐵心端部作用導致[1]。理論上，可得到直線電機的齒槽力矩波動和邊端效應的數學表達式為

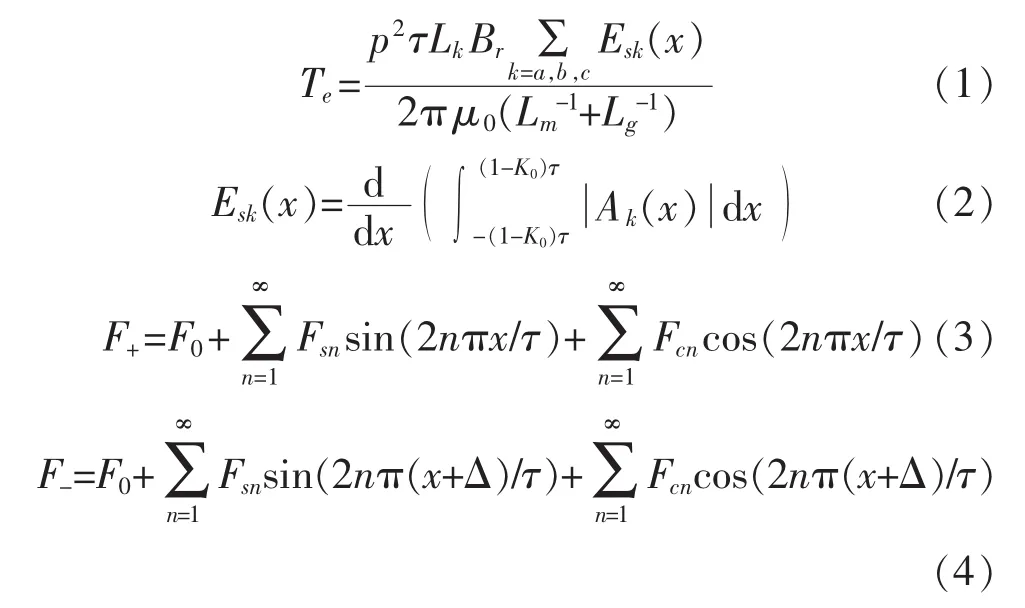
式中：τ為極距；Lg為氣隙長度；Lm為磁鋼厚度；Br為徑向磁密；Lk為鐵芯長度；Δ＝Lk+iτ表示動子鐵芯橫跨的極距；p為直線電機極對數；μ0為磁導率；x為距離軸線的距離。由直線電機的定位力數學表達式可以得到，直線電機的定位力是一個與直線電機位置有關的非線性函數，而且具有一定周期性。然而，數學表達式僅僅在理論分析過程中有較好的作用，在實際應用過程中，由于電機制作、裝配等原因導致的電機參數各處不同且與理論計算有一定差距，因而需要使用合適的方法對直線電機的定位力進行辨識。

2 神經網絡及遺傳算法原理

2.1 人工神經網絡

人工神經網絡是依據仿生學的原理，模擬人腦神經系統的工作方式，使機器具有類似于神經網絡一樣的感知、推理和學習能力，進而用來處理一些比較復雜的問題。神經網絡的實質是一個非線性系統，通過各權值與閾值之間的相互關系及各節點輸入輸出的局部非線性來實現整個網絡模型的非線性映射關系。神經網絡的應用通常具有以下顯著特點：具有很強的自適應和自組織能力，通過學習和訓練來逼近非線性映射關系；信息處理并行化，實現并行處理信息的方式，提高運算的效率。在眾多人工神經網絡的類型中，BP神經網絡應用最為廣泛。BP神經網絡是一種多層前饋神經網絡，如圖1所示，其主要特點是信號向前傳遞，誤差反向傳遞。信號前向傳遞過程中，輸入信號經隱含層處理輸出，每一層神經元影響下一層神經元狀態，如果輸出層得不到期望輸出則反向傳播，改變閾值和權值，使得神經網絡不斷逼近期望輸出，從而使整個網絡逼近所需的非線性映射關系。

圖1 BP神經網絡拓撲結構Fig.1 BP neural network topology structure diagram

BP神經網絡學習和訓練過程如圖2所示，首先進行網絡的初始化，包括輸入層、隱含層與輸出層節點數的確定和網絡各權值與閾值初值的初始化等。其次需要按照式（5）、（6）分別對隱含層與輸出層的輸出進行計算。

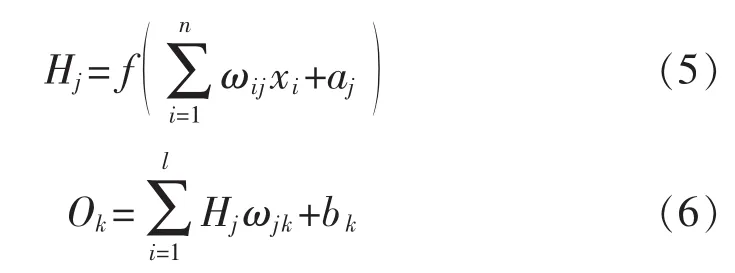
式中：Hj為第j個隱含層節點輸出；Ok為第k個輸出層節點輸出；ωij、ωjk分別為輸入層與隱含層和輸出層之間的權值；a、b則分別為隱含層與輸出層的閾值。

最后按式（7）和式（8）由誤差e對各權值和閾值進行更新：

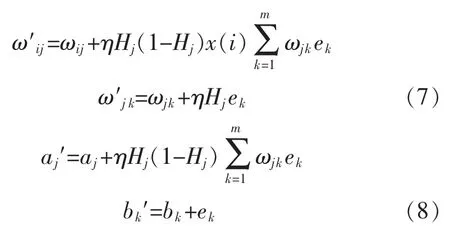
式中，η為學習率。

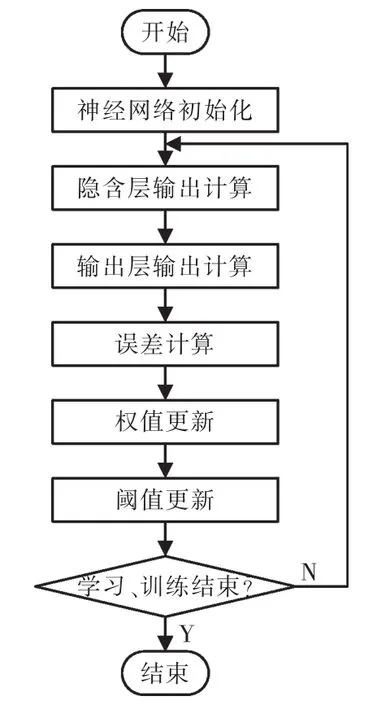
圖2 BP神經網絡算法流程Fig.2 BP neural network algorithm flow chart

2.2 遺傳算法

遺傳算法是基于自然界遺傳機制和生物進化論而形成的一種并行隨機搜索最優化方法。其模擬生物界中自然選擇和群體遺傳機制，采用簡單的編碼技術來表示各種復雜的結構，并通過一組編碼表示和進行簡單的遺傳操作以及優勝劣汰的自然選擇來指導學習和確定搜索的方向[3]。對于一個確定的種群，遺傳算法大致通過以下幾個過程實現：

選擇遺傳算法的選擇操作有多種方法，大致可歸納為輪盤賭法、隨機聯賽選擇法等23種方法[4]。遺傳算法通過適應度選擇優質個體而拋棄劣質個體，體現了“適者生存”的原理[5]。

變異遺傳算法依據算法中設定的變異率對已經進行編碼的個體隨機選擇基因進行改變，以產生新的個體，進而提高局部搜索能力。

交叉遺傳算法對應于個體的編碼形式采用適合的交叉方法交換個體間的基因，從而實現個體的進化。

遺傳算法的算法流程如圖3所示。

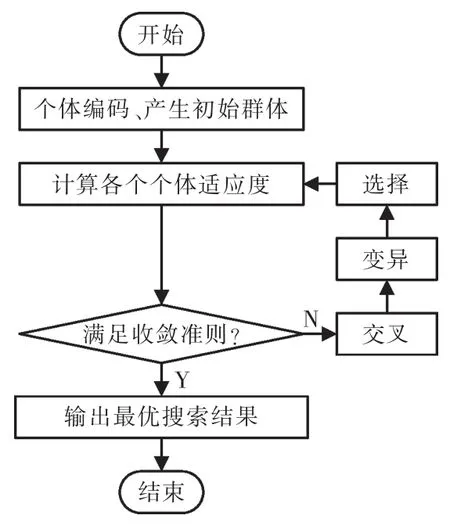
圖3 遺傳算法流程Fig.3 Genetic algorithm flow chart

3 直線電機定位力辨識

3.1 辨識方法

BP神經網絡使用廣泛，算法已經十分成熟，因而在辨識中采用BP神經網絡為辨識模型主體。BP神經網絡雖然可以完成對所需的非線性映射的逼近，但是其計算效率和結果均具有可以進一步優化的余地。均衡考慮計算復雜度與結果精度，使用遺傳算法對神經網絡進行優化。遺傳算法優化BP神經網絡的本質是通過遺傳算法獲得更好的神經網絡初始權值及閾值，即用個體代表網絡的初始權值和閾值，將預測誤差作為個體的適應度函數，通過變異、交叉和選擇等操作收斂得到最優個體，從而實現對BP神經網絡的優化。具體算法如圖4所示。

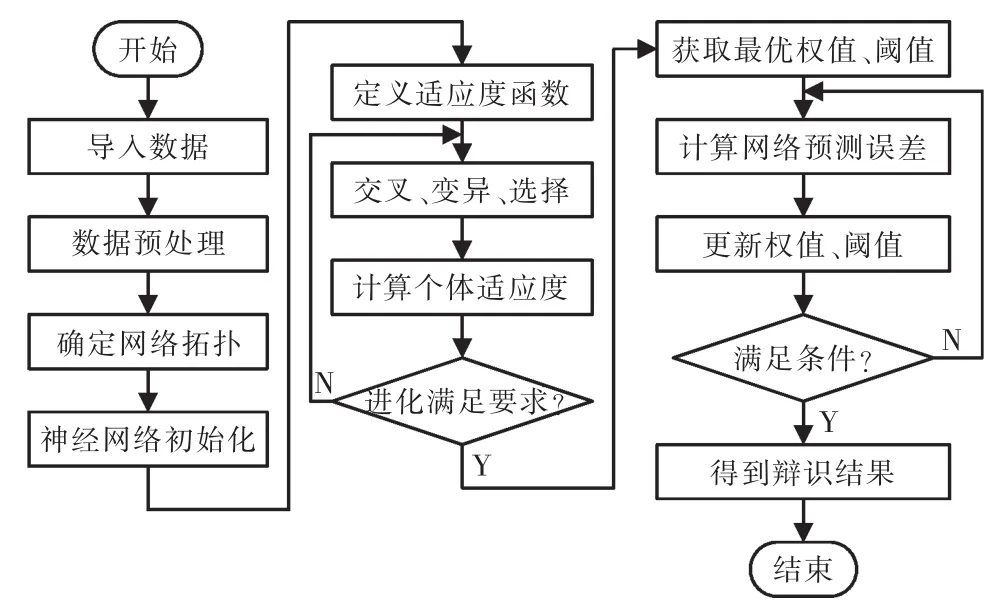
圖4 遺傳算法優化BP神經網絡辨識流程Fig.4 Identification flow chart of BP neural network optimized by GA

3.2 辨識實驗配置與結果

被辨識的目標直線電機在水平與垂直方向均采用氣浮支撐，該機械結構使得機械摩擦等具有近零特性，可盡可能減小機械摩擦阻力的影響；動子位移數據采用分辨率為50 nm的增量式光柵尺進行采集，整個系統采樣頻率為5000 Hz。由電機的動力學方程可得，除了近零機械摩擦力，還需盡可能降低運動的粘滯摩擦力和電機磁阻推力。考慮到運動的粘滯摩擦力正比于速度、磁阻推力正比于繞組電流，直線電機在低勻速狀態下可將二者影響降至最低，因而令直線電機以0.01 m/s勻速運動，利用加速度計得到加速度曲線，進而得到電機定位力波動曲線，其中加速度曲線如圖5所示。

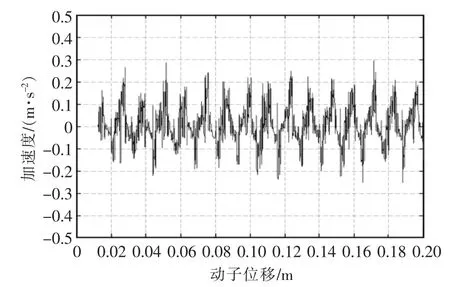
圖5 加速度曲線Fig.5 Diagram of acceleration curve

在所得10000組數據中選擇8000組數據用于遺傳算法優化神經網絡對定位力波動進行辨識，并利用2000組數據驗證辨識模型的可行性。辨識結果如圖6所示。

由仿真得到定位力波動辨識均方誤差為0.224802，結合圖6可以得到遺傳算法優化神經網絡比較精確地對定位力進行了辨識。

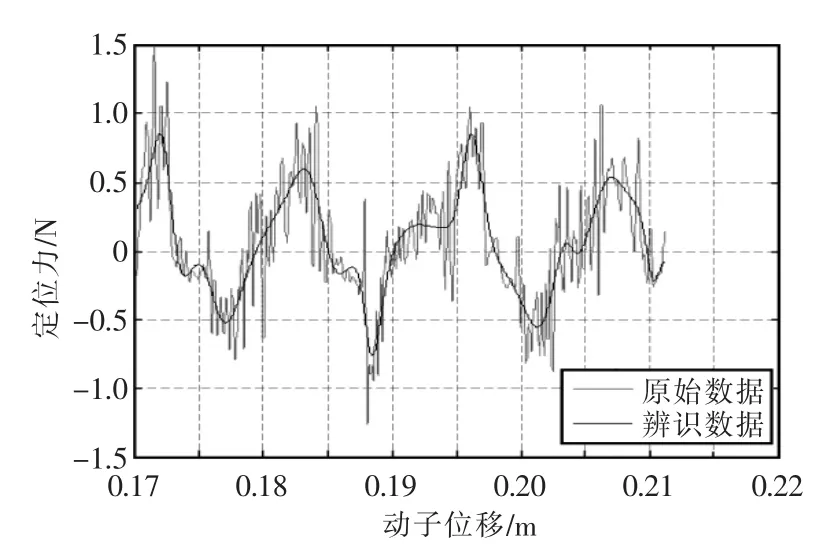
圖6 定位力辨識結果Fig.6 Identification result of cogging force

4 結語

針對工程中需要解決的直線電機定位力波動問題，本文給出了一種基于遺傳算法優化神經網絡的辨識方法。理論分析及實驗表明該方法具有自適應性、應用局限小等優點，并且該方法在實際工程辨識的過程中具有可行性，具有良好的應用價值。

[1]陳興林，楊天博，劉楊.直線電機定位力波動的辨識及迭代補償方法[J].電機與控制學報，2015，19（2）：60-65.

[2]穆海華，周云飛，溫新，等.直線電機齒槽推力波動的標定與補償方法[J].電機與控制學報，2009，13（5）：721-727.

[3]徐磊.基于遺傳算法的多目標優化問題的研究與應用[D].長沙：中南大學，2007.

[4]Potts J C，Giddens T D，Yadav S B.The development and evaluation of an improved genetic algorithm based on migration and artificial selection[J].Systems Man& Cybernetics IEEE Transactions on，1994，24（1）：7-86.

[5]葛繼科，邱玉輝，吳春明，等.遺傳算法研究綜述[J].計算機應用研究，2008，25（10）：2911-2916.

[6]王小川，史峰，郁磊，等.MATLAB神經網絡43個案例分析[M].北京：北京航空航天大學出版社，2013.