基于M估計的抗野值單站無源定位方法?

(火箭軍工程大學,陜西西安710025)

0 引言

單站無源定位技術[1-2]是指利用一個觀測平臺上的單個或多個接收機,通過被動接收目標輻射源的輻射信息來對其進行定位和跟蹤的技術,具有電磁隱蔽性好、設備相對獨立、作用距離遠和易于工程實現等優點。現有的單站無源定位方法主要有測向定位法、到達時間定位法、多普勒頻率定位法、方位/到達時間定位法、相位差變化率定位法和多普勒頻率變化率定位法等,用到的濾波算法主要有擴展卡爾曼濾波(Extended Kalman Filter,EKF)[3-4]、無跡卡爾曼濾波(Unscented Kalman Filter,UKF)[5-6]和容積卡爾曼濾波(Cubature Kalman Filter,CKF)[7-8]等。楊曉君等[9]在EKF算法的基礎上,提出了基于相位差、相位差變化率和頻率變化率的單站無源定位方法(PFRC),該方法具有較高的定位精度和較快的收斂速度。

上述大多數方法都是建立在觀測信息準確的基礎上。然而,在實際問題中,由于測量設備本身出現故障或者環境干擾、目標機動等的影響,觀測數據不可避免會出現野值。統計學家根據大量數據指出,在生產實際和科學實驗中,野值的出現約占觀測總數的1%～10%[10]。野值的出現使得觀測數據的可靠性和可用性下降,降低了定位精度,甚至無法定位。

目前,已有大量文獻對野值存在時如何保持估計量的最優性進行了論述,但有關單站無源定位跟蹤問題的研究中,涉及野值處理問題的文獻較少。例如,文獻[5,11-13]研究了野值存在時如何辨識并剔除的方法;文獻[6,14-16]指出,錯誤的觀測量主要通過新息對濾波精度產生影響,因而對新息進行修正能較好地保持濾波精度;文獻[17]將野值剔除法與新息修正法相結合達到抗野值效果;文獻[7,18]基于Bayes定理并結合歸一化受污染正態模型,根據野值出現的后驗概率來自適應調整新息的方差陣,以降低野值的影響。本文在單站無源定位PFRC方法基礎上,提出了一種基于 M估計的抗野值單站無源定位方法,該方法通過建立新息的非線性函數作為權函數,對新息進行權值修正,較好地消除了野值分量的影響。

1 單站無源定位方法

1.1 單站無源定位模型

單站無源定位系統的狀態方程和觀測方程可表示為

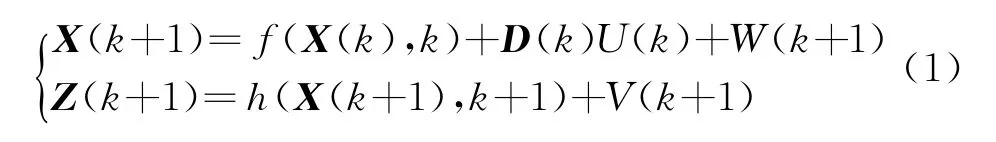
式中:k是時刻;X(k+1)是目標狀態向量,包含目標的位置、速度等信息;Z(k+1)是包含噪聲的觀測向量;f和h分別是非線性狀態函數和非線性測量函數;D(k)是激勵矩陣;U(k)為未知加速度;W(k+1)和V(k+1)分別是過程噪聲和測量噪聲,彼此獨立且服從Gauss分布,它們的協方差矩陣分別為Q(k+1)和R(k+1)。

在PFRC方法中,測量向量包括相位差、相位差變化率、頻率變化率。因此,非線性測量函數可表示為

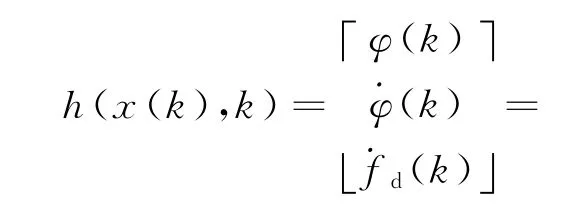
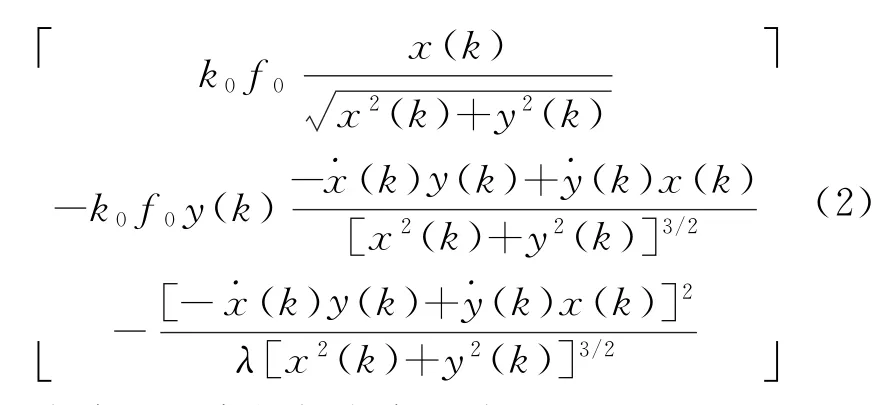
濾波過程中的新息定義為

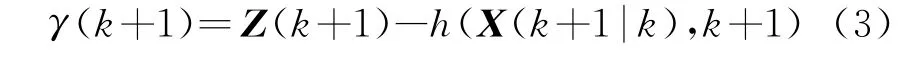
它隱含了當前最新觀測值Z(k+1)的信息,是實際觀測值與預測值(擬合值)之間的差,故又稱為殘差序列。

1.2 野值的影響分析

在單站無源定位理想模型中,當濾波達到穩態時,新息γ(k+1)應為零均值的獨立正態同分布隨機序列,在這種情況下,卡爾曼濾波器對狀態的估計值可以達到很高的精度。但實際情況中,觀測數據不可避免會出現野值。不妨假設k時刻出現野值,并把野值看作疊加于正常觀測數據上的一個沖擊分量,則觀測方程變為

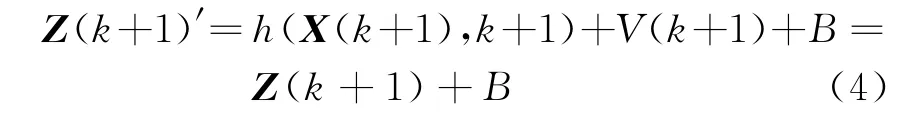
式中,Z(k+1)′為疊加野值分量后的觀測值,B為沖擊形式的野值分量。

則加入野值后得到的新息序列為

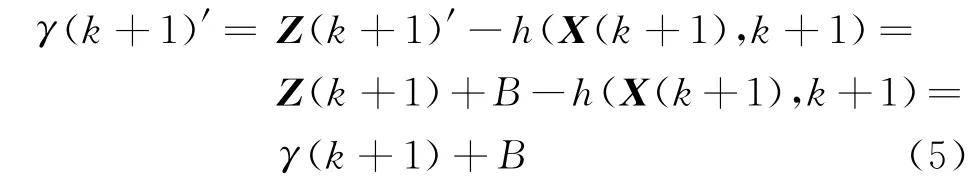
由此可見,野值分量的影響主要體現在新息序列上。在野值分量出現的時刻必須采取適當的措施對新息序列進行校正,才能消除野值對估值精度的影響。

在觀測值中,野值的表現形式主要有以下兩種[5]:

1)孤立型野值,表現為k時刻的觀測數據為野值時,在k的某一個領域內的其他觀測數據是正常的,即野值的出現是孤立的。

2)斑點型野值,表現為k,k+1,k+2,…,k+p時刻的觀測值均嚴重偏離真值,即野值成片出現。

常用的野值處理方法有直接剔除法和新息修正法。直接剔除法能較徹底地消除野值分量的不良影響,但當大量孤立型野值出現,或者大片斑點型野值出現時,直接剔除受野值污染的觀測值會導致數據缺失嚴重,仍然會降低定位精度,甚至使濾波器發散。而僅對新息進行平滑修正,雖能保留觀測序列的完整性,但當野值分量值較大時,難以消除野值的不良影響。本文采用基于M估計法對新息進行權值修正,在考慮野值分量水平的情況下,將觀測值分為正常觀測值、不正常但可以利用觀測值,以及不可利用觀測值這三類,既能保留可利用的觀測值,又可以較徹底地消除野值分量的影響。

2 M估計在單站無源定位中的應用

2.1 M估計的定義

抗差估計[19]或稱穩健估計是指在粗差不可避免的情況下,選擇適當的估計方法使估計量盡可能減少粗差的影響,得出正常模式下的最佳估值。抗差估計包括M估計、L估計和R估計。其中, M估計是經典的極大似然估計的推廣,稱為廣義極大似然型估計。

傳統的極大似然估計(MLE),其估計量T n= T n(x1,x2,…,x n)需滿足

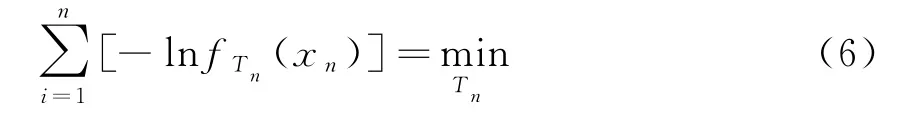
式中,f是隨機變量(x1,x2,…,x n)的概率密度。

1964年Huber用函數ρ代替式(6)中的-lnf(·)使其廣義化:

式中,ρ(·)稱為極值函數。假設ρ(·)的導數為是待估參數,它包括定位參數和尺度參數,于是式(7)可以寫為

式(7)和式(8)均可用于定義M估計,當ψ函數是ρ函數的導數時,式(7)和式(8)定義的M估計等價。

常用的ρ函數是對稱的、凸的或在正半軸上非降的函數,而ψ函數常取成這種ρ函數的導數。當然,ψ函數也可根據需要適當選取。有一個ρ(或ψ)函數就定義一個M估計,因此M估計實際上是一類估計,故稱為廣義極大似然型估計。顯然,經典的極大似然估計是M估計的特例。

2.2 單站無源定位中的M估計

式中,ρ(·)表示適當選擇的凸函數,n表示觀測向量維數,γ(k)i表示時刻k新息序列的第i個元素。式(8)定義的M估計則可表示為

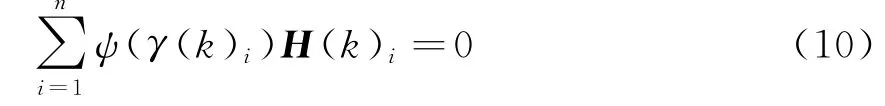
式中:ψ(·)也是適當選擇的單調、正半軸非降函數;H(k)i是測量函數h(X(k),k)的偏導矩陣H(k)的第i行向量。令

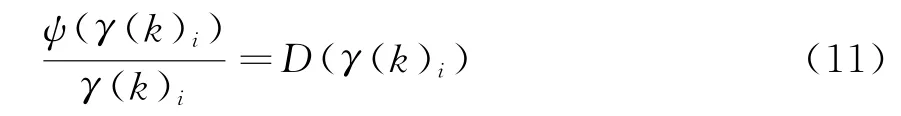
則式(10)可寫成

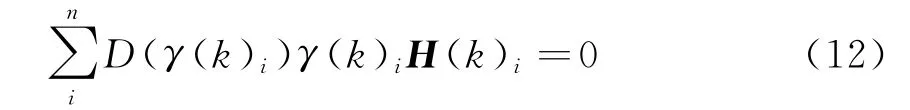
式中,D(γ(k)i)可看成權函數。式(12)寫成矩陣形式為

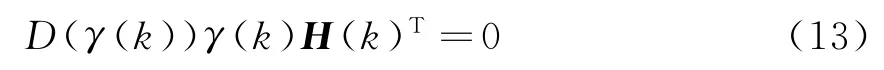
式中,D(γ(k))=diag[D(γ(k)1),D(γ(k)2),…,D(γ(k)n)]。

從式(11)可以看出,權函數D(γ(k)i)是新息序列的非線性函數。所以,M估計的實質是用權函數去修正新息原有的權,它實現抗差化的基本思想是:

1)對于正常觀測值采取保權處理,即令D(γ(k)i)=1,此時,M估計退化為最小二乘估計。

2)對于非正常但又可以利用的觀測值采取降權處理,即令D(γ(k)i)＜1。

3)對于野值超過一定范圍的、不可用的觀測值,使其權為0,予以淘汰,即令D(γ(k)i)=0。

因此,抗差化的關鍵就在于建立恰當的權函數。本文中,權函數D(γ(k)i)由IGG法[19]確定:

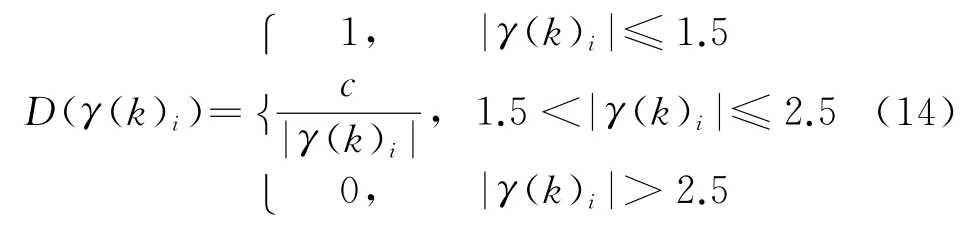
式中,c為一選定的常數。

2.3 基于M估計的單站無源定位方法

本文在文獻[9]提出的PFRC方法基礎上,通過建立新息的非線性函數作為權函數,對新息序列進行權值修正,實現了PFRC算法的抗野值能力。基于M估計的單站無源定位方法步驟如下:

1)時間更新

① 設定初始值

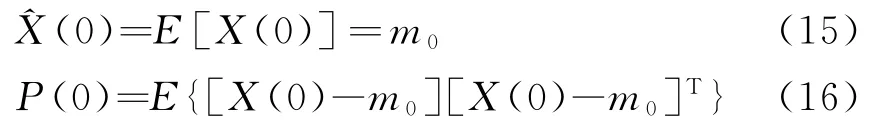
② 一步預測

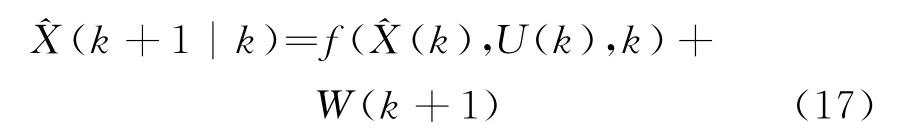
③ 一步預測均方誤差

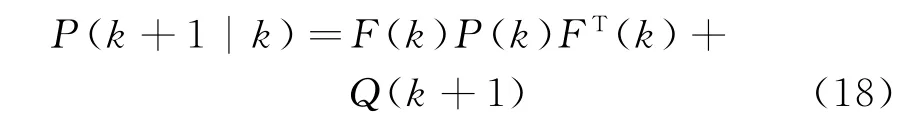
④ 濾波增益

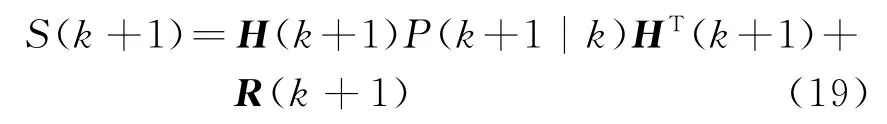
2)測量更新

① 計算測量新息

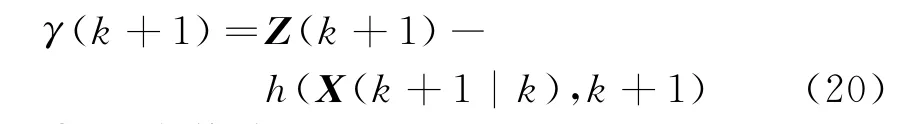
② 狀態估計

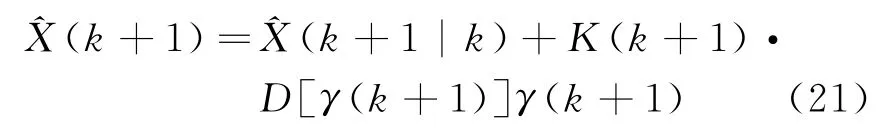
③ 估計均方誤差

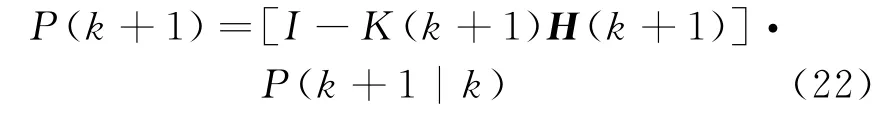
3 仿真實驗

為了檢驗基于M估計的單站無源定位方法的抗野值能力,通過改變野值的水平和式(14)中常數c的值,分別針對孤立型野值和斑點型野值進行Monte-Carlo仿真實驗。

不失一般性,仿真以二維單站無源定位情況為例,假設固定觀測站位于坐標原點,目標輻射源作勻速直線運動,觀測周期為Ts=1 ms,取1 500個觀測點,初始狀態X(0)=[200 m,549 m,-300 m/s,0 m/s],在觀測時間內目標輻射源的頻率保持f=200 M Hz不變。

本文采用相對定位誤差(RPE)和相對速度誤差(RVE)來描述單站無源定位的性能,其定義為

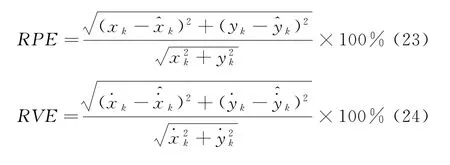
3.1 孤立型野值仿真實驗

選取不同的常數c值,在第600個觀測時刻,對相位差觀測量添加大小不同的野值。圖1和圖2分別展示了c=0.1和c=1.5的情況下,野值的大小為B=2和B=10時的仿真結果。

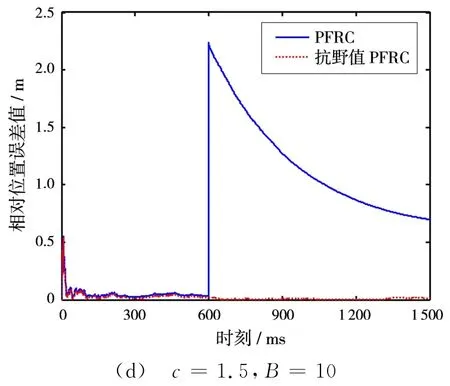
圖1 基于100次Monte-Carlo實驗的相對位置誤差值

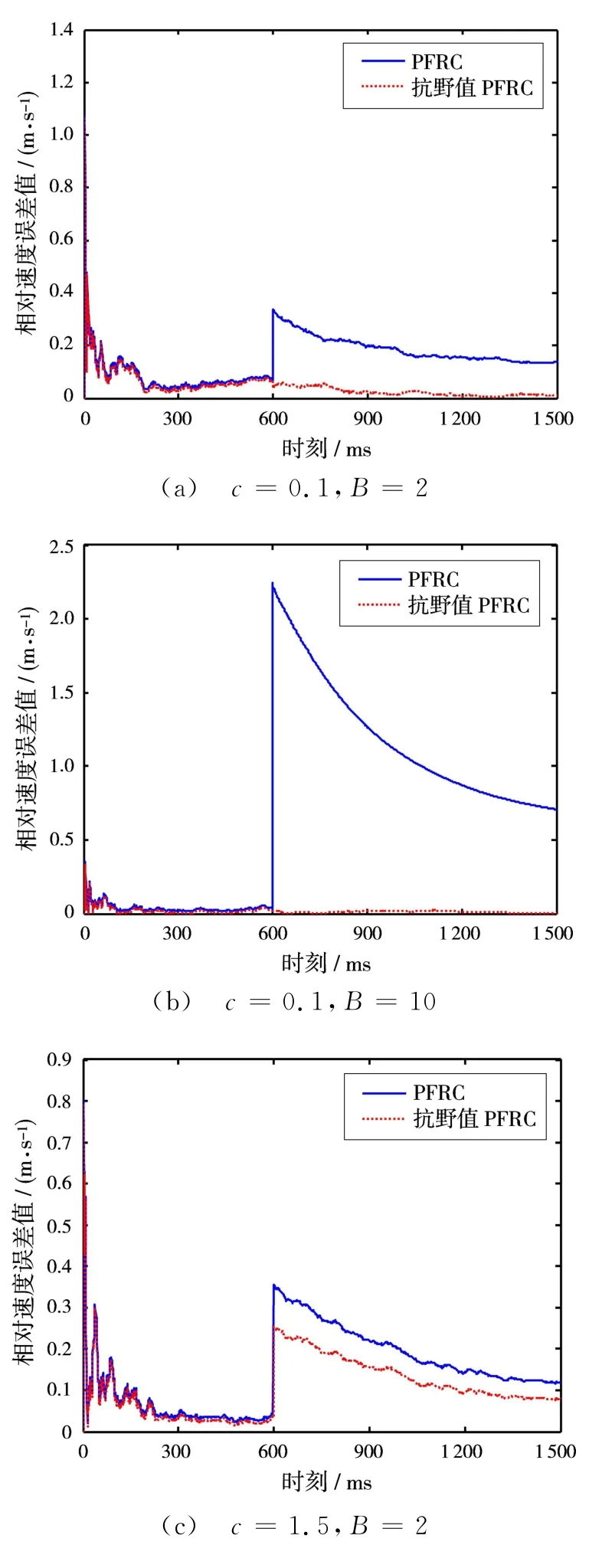
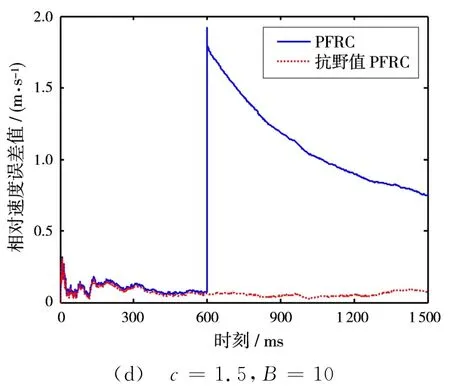
圖2 基于100次Monte-Carlo實驗的相對速度誤差值

通過圖1和圖2可以看出:

1)當觀測量中未出現野值時,兩種算法的定位精度一樣。

2)當觀測量中存在單個野值的時候,PFRC方法的定位精度受到了比較嚴重的影響,這是由于觀測新息突然增大,導致濾波增益也隨之變大,使得估計結果較大地偏離了真實值;而基于M估計的抗野值PFRC方法,能根據新息變化自適應地調整權函數值,通過對新息的權值修正克服野值分量的影響。

3)當常數c取值越小時,抗野值PFRC方法的穩定性就越好,濾波系統也收斂得更快,表現出了較強的魯棒性。

4)當野值分量越大時,抗野值PFRC方法的優越性體現得越明顯。

3.2 斑點型野值仿真實驗

選取常數c=0.1,從第600個觀測時刻開始,連續添加大小為B=2的野值分量。圖3和圖4分別展示了連續5個時刻、10個時刻添加野值時的仿真結果。

通過圖3和圖4可以看出,當觀測量連續出現野值時,PFRC方法的濾波精度受到很大影響,甚至導致濾波器發散;而基于 M 估計的抗野值PFRC方法保持了較好的穩定性,濾波器依舊可以收斂到正常狀態,具有較強的魯棒性。

4 結束語

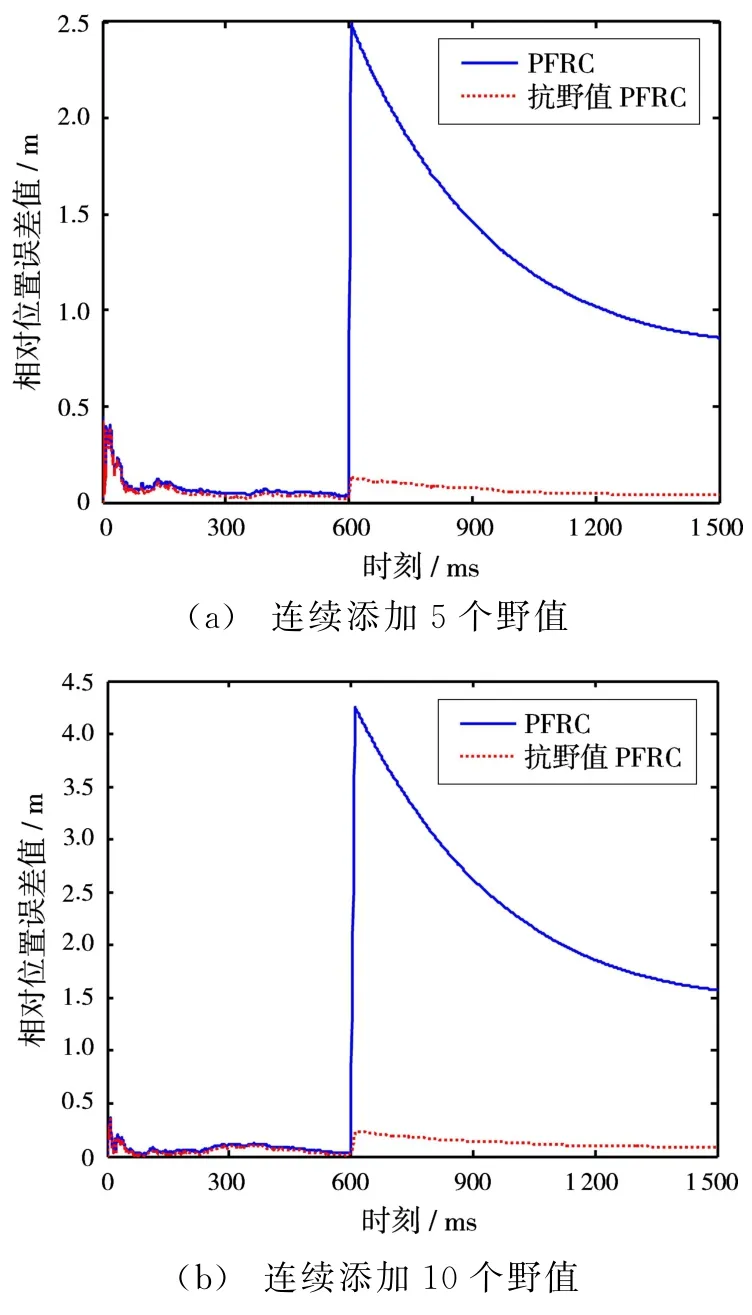
圖3 基于100次Monte-Carlo實驗的相對位置誤差值

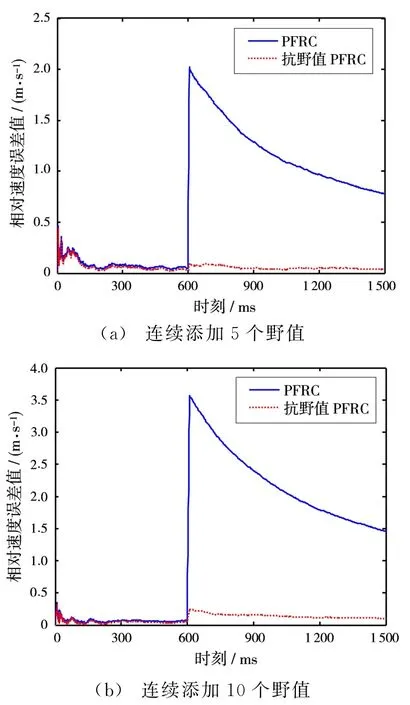
圖4 基于100次Monte-Carlo實驗的相對速度誤差值

在實際情況中,單站無源定位過程中出現野值是不可避免的,野值的存在會影響定位的精度和系統的穩定性,以致嚴重失真和誤判。本文通過建立新息的非線性函數作為權函數,對新息進行自適應權值修正,提出了一種新的基于M估計的抗野值單站無源定位方法。通過對孤立型野值和斑點型野值進行仿真實驗,結果表明,本文的算法能很好地克服野值影響,具有較強的魯棒性和較高的定位精度。并且當不存在野值時,該算法能保持原PFRC算法的精度。

以往在單站無源定位研究中,考慮到野值問題的文獻較少,本文所提方法較好地解決了單站無源定位中的野值問題,具有一定的實用性。

[1]孫仲康,郭福成,馮道旺,等.單站無源定位跟蹤技術[M].北京:國防工業出版社,2008.

[2]楊曉君,陸芳,郭金庫,等.模糊單站無源定位方法[J].清華大學學報(自然科學版),2011,51(1):25-29.

[3]李炳榮,丁善榮,馬強.擴展卡爾曼濾波在無源定位中的應用研究[J].中國電子科學研究院學報,2011,6 (6):622-625.

[4]孟祥飛.基于擴展卡爾曼濾波算法的無源定位效果分析[J].電子科技,2012,25(3):25-27.

[5]張怡,廉晶晶,黃文剛.抗野值性能的無跡卡爾曼濾波算法的研究[J].計算機工程與應用,2012,48(33): 153-156.

[6]張學峰,周超,劉文超.抗野值滑動平均-UKF算法在組合導航中的應用[J].數字技術與應用,2015(2): 133-134.

[7]霍光,李冬海,李晶.單站無源定位中的抗野值魯棒CKF算法[J].雷達科學與技術,2013,11(4):419-423. HUO Guang,LI Donghai,LI Jing.An Outlier Rejecting Robust CKF Algorithm for Single Observer Passive Location[J].Radar Science and Technology, 2013,11(4):419-423.(in Chinese)

[8]霍光,李冬海.基于后向平滑容積卡爾曼濾波的單站無源定位算法[J].信號處理,2013,29(1):68-74.

[9]YANG X,LIU G,GUO J.A Single Observation Passive Location Algorithm Based on Phase-Difference and Doppler Frequency Rate of Change[C]∥2008 IEEE International Conference on Systems,Man and Cybernetics,Budapest,Hungary:IEEE,2008: 1309-1313.

[10]HUBER P J.Robust Statistics[M].New York:Wiley,1981.

[11]楊軍玲.無源定位跟蹤中野值的檢測與剔除方法[J].電子科技,2016,29(6):51-53.

[12]盧元磊,何佳洲,安瑾.目標預測中的野值剔除方法研究[J].計算機與數字工程,2013,41(5):722-725.

[13]張強,孫紅勝,胡澤明.目標跟蹤中野值的判別與剔除方法[J].太赫茲科學與電子信息學報,2014,12 (2):256-259.

[14]武昱,曹鑫,錢克昌,等.一種魯棒的Kalman濾波方法[J].計算機與數字工程,2013,41(5):716-718.

[15]戴文舒,陳新華,孫長瑜,等.等價權修正的Kalman抗野值濾波算法[J].應用聲學,2013(5):409-412.

[16]朱占龍,單友東,楊翼,等.基于新息正交性自適應濾波的慣性/地磁組合導航方法[J].中國慣性技術學報,2015,23(1):66-70.

[17]李廣軍,李忠,崔繼仁.新型抗野值的Kalman濾波器研究[J].計算機應用與軟件,2013,30(1):136-138.

[18]賈浩正.抗野值的航跡數據Kalman濾波[J].測控技術,2014,33(9):26-28.

[19]周江文,黃幼才,楊元喜,等.抗差最小二乘法[M].武漢:華中理工大學出版社,1997.